MULTIOBJECTIVE TUNING OF ROBUST GPC CONTROLLERS
USING EVOLUTIONARY ALGORITHMS
J. M. Herrero, X. Blasco, M. Martínez and J. Sanchis
Instituto Universitario de Automática e Informática Industrial, Universidad Politécnica de Valencia
Camino de Vera s/n, 46022 Valencia, Spain
Keywords:
Multiobjective optimization, Evolutionary algorithms, Predictive control.
Abstract:
In this article a procedure to tune robust Generalized Predictive Controllers (GPC) is presented. To tune
the controller parameters a multiobjective optimization problem is formulated so the designer can consider
conflicting objectives simultaneously without establishing any prior preference. Moreover model uncertainty,
represented by a list of possible models, is considered. The multiobjective problem is solved with a specific
Evolutionary Algorithm (ev-MOGA). Finally, an application to a non-linear thermal process is presented to
illustrate the technique.
1 INTRODUCTION
Generalized predictive control (GPC) (Clarke et al.,
1987a) (Clarke et al., 1987b) has been shown to be an
effective way of controlling single-input single-output
processes. The strategy proposed by GPC is simple to
understand and makes good practical sense: predict
the behaviour of the output as a function of future con-
trol increments and minimize over these increments a
cost index. This cost includes the errors between pre-
dicted and desired outputs and the control effort. De-
spite its advantages, tuning GPC methods are based
on a linear models, which are usually adjusted around
an operating point. When the process operates out-
side the validity zone of the model (where differences
between model and process behaviour increase) poor
control performance is obtained since in that case the
tuning is suboptimal even close-loop stability could
take place.
To avoid that, robust GPC tuning approach is as-
sumed. In this case model uncertainties are taking
into account to cover non-modelled dynamics (such
as non linearities, high frequency dynamics, and so
on) and measurement noise (Reinelt et al., 2002). The
simpler the model is the bigger uncertainties are, pro-
ducing an excess of conservativeness in the tuning
result, which give as a result a loss of performance
in the close-loop control. Therefore the goal is to
achieve robust tunings with good performance at the
same time, for instance, minimizing error or control
effort. Objectives that are usually in contraposition.
The GPC tuning methodology that is presented
tries to achieve that goal by:
• Using non-linear parametric models with uncer-
tainty. The uncertainty is consider by means of a
set of models, the Feasible Parameter Set (FPS
∗
).
Although the real process is not known, assume
that it lies within the FPS
∗
(Walter and Piet-
Lahanier, 1990).
• Proposing a Multiobjective optimization (MO)
GPC tuning approach.
Optimal tuning considers not only a nominal model
but the FPS adjusting the controller parameters for
the worst case (the most unfavorable model). More-
over, because the tuning method has to consider
conflicting objectives, an optimization multiobjective
problem is stated where each objective minimizes the
maximum cost function for all the models in the un-
certainty description.
Multiobjective optimization (MO) techniques
present advantages as compared with single objective
optimization techniques due to the possibility of giv-
ing a solution with different trade-offs among differ-
ent individual objectives so that the Decision Maker
(DM) can select an appropriate final solution.
The presence of multi-modal MO functions and
non-convex constrined spaces needs optimizer with
good performance. A good choice are stochastic op-
timizers such as the Evoluationary Algorithms (EAs)
(Coello et al., 2002) that can work well with multi-
modal and non-convex problems, in particular, the al-
263
M. Herrero J., Blasco X., Martínez M. and Sanchis J. (2009).
MULTIOBJECTIVE TUNING OF ROBUST GPC CONTROLLERS USING EVOLUTIONARY ALGORITHMS.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 263-268
DOI: 10.5220/0002269102630268
Copyright
c
 SciTePress

gorithms used in this work will be the ev-MOGA one
(Herrero et al., 2007c; Herrero et al., 2007b).
This paper is organized as follows. Section 2
presents GPC formulation, section 3 introduces tun-
ing procedure proposed in this article, section 4 de-
scribes briefly used. Section 5 illustrates the GPC tun-
ing procedure with the example of a thermal process.
Finally, some concluding remarks are reported in sec-
tion 6.
2 GPC FORMULATION
The GPC formulation with quadratic cost index has
been extensively developed in (Clarke et al., 1987a),
(Clarke et al., 1987b). Such formulation uses the fol-
lowing CARIMA stochastic model:
y(t) =
B(z
−1
)
A(z
−1
)
u(t − 1) +
T(z
−1
)
∆A(z
−1
)
d(t) (1)
where: u(t) and y(t) are the process input and out-
put respectively, d(t) the disturbance (white noise),
T(z
−1
) is a polynomial used to filter disturbance and,
B(z
−1
) and A(z
−1
) are the polynomial transfer func-
tion of the discrete model. A GPC controller is ob-
tained through the optimization of the following cost
index and applying Receding Horizon:
J(∆u) = E[
N
2
∑
i=N
1
α[y(t + i) − r(t)]
2
+
N
u
∑
j=1
λ[∆u(t + j − 1)]
2
]
(2)
where N = N
2
− N
1
+ 1 is the prediction hori-
zon, N
u
is the control horizon, α is the pre-
diction error weighting factor, λ is the con-
trol weighting factor, r(t) is the setpoint, and
[
∆u(t) ∆u(t + 1) · · · ∆u(t + N
u
− 1)
]
T
are the
control actions.
Optimizing index (2) and applying Receding
Horizon (so that, using only ∆u(t)) the following GPC
expression is obtained:
u(z) =
T(z
−1
)

H
0
r(z) −
S(z
−1
)
T(z
−1
)
y(z)

(T(z
−1
) + R(z
−1
)z
−1
)∆
Figure 1 represents implementation of this controller
with a block diagram.
3 MULTIOBJECTIVE TUNING
OF ROBUST GPC
Let’s assume the following model structure:
˙
x(t) = f(x(t), u(t), θ), ˆy(t, θ) = g(x(t), u(t), θ) (3)
r
u
1
( )
1 1 1
( ( ) ( ))
T z
T z z R z
-
- - -
+ D
1
1
( )
( )
S z
T z
-
-
o
H
y
*
M odel
FPS
Tra jectory
Generator
Figure 1: Control structure for GPC. r represents the set
point for the output y.
where: f(.), g(.) are the non-linear functions of the
model; θ ∈ R
L
is the vector of unknown model pa-
rameters; x(t) ∈ R
n
is the vector of model states; u(t)
is the input process and ˆy(t, θ) the output.
Asume θ
n
are the parameters of the nominal
model which belong to FPS
FPS := {θ
1
, . . . , θ
p
} (4)
that represents the model parameters uncertainty.
The possible controller parameters to tune are k =
{N
1
, N
2
, N
u
, α, λ, T(z)}. To obtain the controller the
following MO problem can be formulated:
min
k∈D
J(k) = min
k∈D
[J
1
(k), J
2
(k), . . . , J
s
(k)] (5)
where J
i
(k), i ∈ B := [1. . . s] are the objectivesto min-
imize and k is a solution inside the solution space D.
Since each objective to minimize has to take into
account the model uncertainty FPS
∗
then
J
i
(k) = max
θ∈FPS
∗
φ
i
(6)
where the cost function φ
i
is the real objective to min-
imize for the worst model case belonging to FPS
∗
.
Some typical criteria are: the norm of the control ac-
tion: φ
i
= ||u(t)||, the norm of the rate of change of
control action: φ
i
= ||∆u(t)||, the norm of the error:
φ
i
= ||r(t) − y(t)|| or the norm of the error weighted
with time: φ
i
= ||t(r(t) − y(t))||.
Anyway, to solve the MO problem the Pareto op-
timal set K
P
(solutions where no-one dominates oth-
ers) must be found. K
P
is unique and normally in-
cludes infinite solutions. Hence a set K
∗
P
(which is not
unique), with a finite number of elements from K
P
,
should be obtained (see (Coello et al., 2002) for de-
tails of MO problems). To obtain K
∗
P
a MOEA known
as the ev-MOGA algorithm (Herrero et al., 2007c;
Herrero et al., 2007b) will be used.
Finally a unique solution k
∗
of the Pareto optimal
set K
∗
P
has to be selected. The selection procedure is
based on designer preferences and can differsdepend-
ing on design needs. Since all Pareto optimal points
are non-dominated any selection made will be always
optimal.
IJCCI 2009 - International Joint Conference on Computational Intelligence
264

4 EV-MOGA ALGORITHM
ev-MOGA (previously called εր-MOGA, (Herrero
et al., 2007b; Herrero et al., 2007c)) is an elitist mul-
tiobjective evolutionary algorithm based on the con-
cept of ε-dominance (Laumanns et al., 2002). A com-
pleted and detailed version of ev-MOGA algorithm is
developed in (Herrero, 2006) where the performance
of the algorithm is tested by facing up to classical
benchmarks for MO. It obtains an ε-Pareto set, K
∗
P
,
that converges towards the Pareto optimal set K
P
in
a distributed manner around Pareto front J(K
P
), with
limited memory resources. Next a brief description of
the ev-MOGA algorithm is presented.
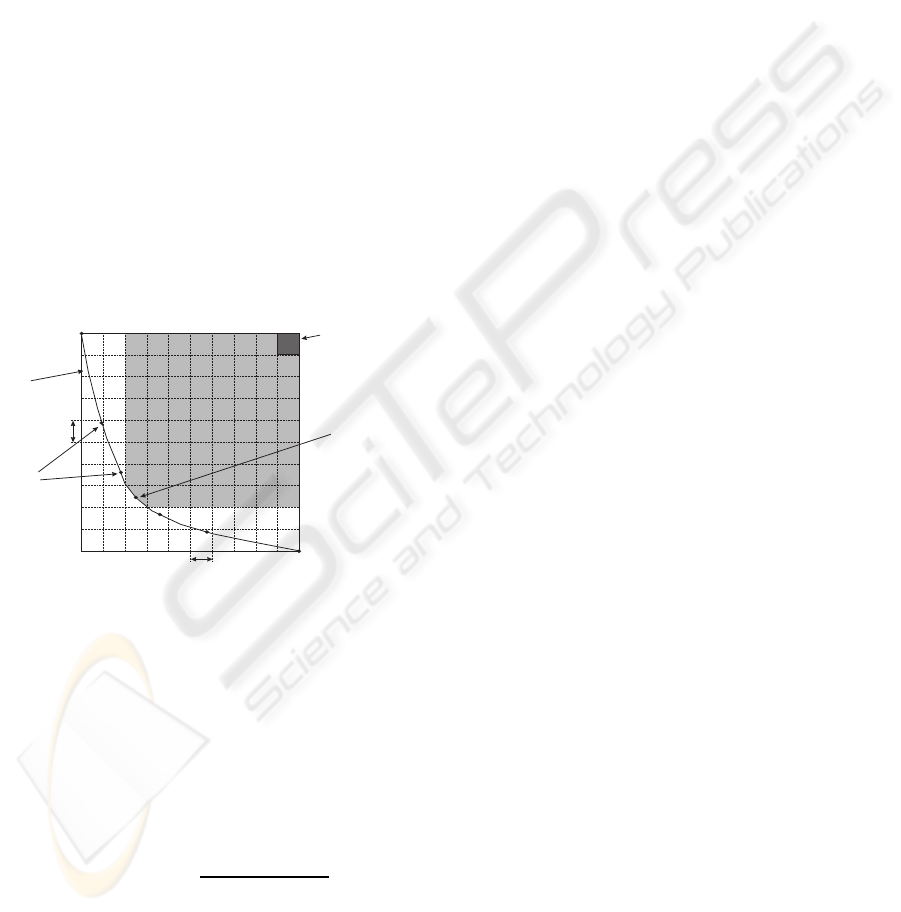
ev-MOGA adjusts the limits of the Pareto front
J(K
∗
P
) dynamically and preventsthe solutions belong-
ing to the ends of the front from being lost. For this
reason, the objective spaceis split up into a fixed num-
ber of boxes n_box
i
, for each dimension i, so that this
grid preserves the diversity of J(K
∗
P
) since one box
can be occupied by only one solution. This fact pre-
vents that the algorithm converges towards just one
point or area inside the objective space (see Fig. 2).
J1
max
J1
min
J2
min
J2
max
e1
e2
n_box =10
1
n_box =10
2
J(K
P
)
J(K
P
)
*
J(k
i
)
Greyareais
-dominatedbye
arethe
points
k
i
box
Figure 2: The concept of ε-dominance. ε-Pareto Front
J(K
∗
P
) in a two-dimensional problem. J
min
1
, J
min
2
, J
max
1
,
J
max
2
, Pareto front limits; ε
1
, ε
2
box widths; and n_box
1
,
n_box
2
, number of boxes for each dimension.
The algorithm is composed of three populations:
The main population P(t) which explores the search-
ing space D during the algorithm iterations (t). Its
Population size is Nind
P
; the archive A(t) which
stores the solution K
∗
P
. Its size Nind
A
can vary but
it will never be higher than
Nind_max_A =
∏
s
i=1
n_box
i
+ 1
n_box
max
+ 1
(7)
where n_box
max
= max([n_box
1
, . . . , n_box
s
]) and the
auxiliary population G(t). Its size is Nind
G
, which
must be an even number.
The pseudocode of the ev-MOEA algorithm is
given by
1. t:=0; A(t):=
/
0 ;
P(t):=ini_random( D )
2. eval(P(t))
3. A(t):=store
ini
(P(t),A(t))
4. while t<t_max {
5. G(t):=create(P(t),A(t))
6. eval(G(t))
7. A(t+1):=store(G(t),A(t))
8. P(t+1):=update(G(t),P(t))
9. t:=t+1 }
The main steps of the algorithm are detailed as
follows:
Steps 2 and 6. Function eval calculates function
value (Equation (5)) for each individual in P(t)
(step 2) and G(t) (step 6).
Step 3. Function store
ini
checks individuals of P(t)
that might be included in the archive A(t) as fol-
lows:
1. Non-dominated P(t) individuals are detected,
K
ND
.
2. Pareto front limits J
max
i
and J
min
i
are calculated
from J(k), ∀k ∈ K
ND
.
3. Individuals in K
ND
are analyzed, one by one,
and those that are not ε-dominated by individu-
als in A(t), will be included in A(t).
Step 5. Function create creates individual of G(t) by
using linear recombination technique and random
mutation with Gaussian distribution.
Step 7. Function store checks, which individuals in
G(t) must be included in A(t) on the basis of their
location in the objective space. Only individu-
als which are not ε-dominated by any individual
from A(t) will be included (if its box is occu-
pied by an individual not ε-dominated too, then
the individual lying farthest away from the cen-
tre box will be eliminated). Individuals from A(t)
which are ε-dominated by individual of G(t) will
be eliminated. Also this function updates the lim-
its J
max
i
, J
min
i
of the Pareto front if it is necessary.
Step 8. Function update updates P(t) with individ-
uals from G(t). Every individual k
G
from G(t)
is compared with an individual k
P
randomly se-
lected from P(t). If k
G
dominates k
P
then k
G
re-
places k
P
. k
P
will not be included in P(t) if there
is no individual in P(t) dominated by k
G
.
Finally, individuals from A(t) compound the MO
problem solution K
∗
P
.
MULTIOBJECTIVE TUNING OF ROBUST GPC CONTROLLERS USING EVOLUTIONARY ALGORITHMS
265

5 ROBUST GPC TUNING FOR A
THERMAL PROCESS
A scale furnace with a resistance placed inside is con-
sidered. A fan continuously introduces air from out-
side (air circulation) while energy is supplied by an
actuator controlled by voltage. Taking into account
heat transfer phenomena (conduction, convection and
radiation) the dynamics of the resistance temperature
can be modelled by
˙x(t) =

θ
1
u(t)
2
− θ
2
(x(t) − T
a
(t)) −
θ
3
(273+x(t))
4
100
4

1000
,
(8)
ˆy(t) = x(t), (9)
where: ˙x(t) is the model state; u(t) is the input
voltage with rank 0 - 100 (%); ˆy(t) is the resistance
temperature (
o
C) (model output); T
a
(t) is the air tem-
perature (
o
C) and θ = [θ
1
, θ
2
, θ
3
]
T
are the model pa-
rameters.
To obtain the (FPS
∗
), which characterize the
model uncertainty, the robust identification method
presented in (Herrero et al., 2007a) was applied. The
FPS
∗
is discrete characterization of the parameter set
which keeps the model predictions error bounded for
certain norms and bounds.
In this example ∞-norm and absolute norm are si-
multaneously used to determine the FPS
∗
. Bounds
are selected in order to hold the FPS
∗
models predic-
tions errors lower than 2
o
C and their average values
lower than 0.8
o
C.
The resulting FPS
∗
contains 304 models (for more
details see (Herrero et al., 2007c)).
The nominal model θ
n
= [0.0776, 4.52, 0.176] ∈
FPS
∗
is linearized in the [y, u] = [56.1, 50] point and
converted to discrete time with T
s
= 10 sample time
obtaining the following model B(z
−1
) = 0.0758z
−1
and A(z
−1
) = 1− 0.9533z
−1
. The following GPC pa-
rameters are fixed N
1
= N
u
= α = 1, T(z
−1
) = A(z
−1
)
whilst N
2
and λ will be tuned. Therefore the search-
ing space is defined by N
2
∈ [5, 6, . . . 100] and λ ∈
[0.1. . . 100]. The functions selected are the follow-
ings:
φ
1
=
||r(t) − y(t)||
1
N
, φ
2
= ||∆u(t)||
1
.
with r(t) = [r(0), r(1 · Ts). . . r(N · T
s
)] and N =
250 is the number of samples.
Then the MO problem to solve is the following:
min
k∈D
[J
1
(k), J
2
(k)] = min
k∈D
[ max
θ∈FPS
∗
φ
1
, max
θ∈FPS
∗
φ
2
]
To solve this MO problem the algorithm ev-
MOGA is used. The parameters of the ev-MOGA
algorithm were set to: Nind
G
= 4; Nind
P
= 100;
t
max
= 1000 (resulting in 4100 evaluations of J
1
(k)
and J
2
(k)) and n_box
1
= n_box
2
= 200. The algo-
rithm was run 10 times.
Fig. 3 shows the best Pareto front and set ob-
tained. Notice that the Pareto front is disjoint, the
same as the Pareto optimal set. The better characteri-
zation of the Pareto front is needed the larger n_box
i
has to be used. ev-MOGA algorithm captures the ex-
tremes of the Pareto front, and thus K
∗
P
will contain
the optimal solutions k
J
i
of each J
i
considered on an
individual basis.
Analyzing the Pareto front (see Fig. 3), the so-
lutions corresponding to higher values of λ (bottom
right area of the Pareto Front) produce bigger control
error as it is expected. Otherwise, the solutions corre-
sponding to lower values of λ and bigger values of N
2
(top left area) produce lowercontrol error in exchange
for bigger control effort.
Therefore, taking into account the Pareto front
and set obtained, the following compromise solution
k
∗
has been selected k
∗
= [12, 6.552] ⇒ J(k
∗
) =
[3.0885, 123.1767].
Fig. 4 shows the envelop generated by the com-
promise controller k
∗
for the output y(t) and input u(t)
when all the models of the FPS
∗
are considered.
6 CONCLUSIONS
A methodology, based on Evolutionary Algorithms,
has been developed to tuning robust GPCs from an
MO point of view. The methodology presents the fol-
lowing features:
• Assuming parametric uncertainty, all kind of pro-
cesses can be considered.
• Since a non-linear models set have been consid-
ered, low uncertainties are produced by the ro-
bust identification process (a difference that a liner
model with interval parametric uncertainty were
considered) and therefore less conservativeness is
produced.
• Any kind of design objectives can be used simul-
taneously to tune the GPC controller resulting in
a MO Problem. Thanks to the ev-MOGA algo-
rithm would be possible to characterize all kind
of Pareto fronts in a well-distributed manner with
bounded memory resources.
IJCCI 2009 - International Joint Conference on Computational Intelligence
266

0 2 4 6 8 10 12 14 16
0
50
100
150
200
250
J
1
(k)
J
2
(k)
0 10 20 30 40 50 60 70 80 90 100
0
20
40
60
80
100
N
2
λ
Figure 3: Top: the ε-Pareto front J(K
∗
P
). Bottom: the Pareto optimal set K
∗
P
. (*) Compromise solution obtained, k
∗
and
J(k
∗
).
0 50 100 150 200 250
30
40
50
60
70
80
90
time(sec.)
r(t) & y(t) envelop
0 50 100 150 200 250
20
30
40
50
60
70
80
90
100
time(sec.)
u(t) envelop
Figure 4: Top: Set point trajectory generated r(t) and the envelop of the outputs y(t) when the controller k
∗
is applied to FPS
∗
models. Bottom: the envelop of the control action produces the envelop of the outputs.
MULTIOBJECTIVE TUNING OF ROBUST GPC CONTROLLERS USING EVOLUTIONARY ALGORITHMS
267

ACKNOWLEDGEMENTS
Partially funded by GVPRE/2008/326 and DPI2008-
02133/DPI.
REFERENCES
Clarke, D., Mohtadi, C., and Tuffs, P. (1987)a). Generalized
predictive control. Part I. Automatica, 23(2):137–148.
Clarke, D., Mohtadi, C., and Tuffs, P. (1987b). Generalized
predictive control. Part II.extensions and. Automatica,
23 (2):149–160.
Coello, C., Veldhuizen, D., and Lamont, G. (2002). Evo-
lutionary algorithms for solving multi-objective prob-
lems. Kluwer Academic Publischers.
Herrero, J. (2006). Identificación robusta de sistemas no
lineales mediante algoritmos evolutivos [Robust iden-
tification of non-linear systems using evolutionary al-
gorithms.]. PhD thesis, Universidad Politécnica de
Valencia, Valencia, Spain.
Herrero, J., Blasco, X., Martínez, M., and Salcedo, J.
(2007a). Non-linear robust identification: Application
to a thermal. Lecture Notes in Computer in Computer
Science, 4527:457–466.
Herrero, J., Martínez, M., Ramos, C., and Sanchis, J.
(2007b). Non-linear robust identification of a green-
house model using multi-objective evolutionary algo-
rithms. Biosystems agriculture, 16 (5):515–530.
Herrero, J., Martínez, M., Sanchis, J., and Blasco, X.
(2007c). Well-distributed pareto front by using the.
Lecture Notes in Computer in Computer Science,
4507:292–299.
Laumanns, M., Thiele, L., Deb, K., and Zitzler, E. (2002).
Combining convergence and diversity in evolution-
ary multi-objective. Evolutionary computation, 10
(3):263–282.
Reinelt, W., Garulli, A., and Ljung, L. (2002). Compar-
ing different approaches to model error modelling in
robust identification. Automatica, 38 (2):787–803.
Walter, E. and Piet-Lahanier, H. (1990). Estimation of pa-
rameter bounds from bounded-error data: A survey.
Mathematics and computers in Simulation, 32:449–
468.
IJCCI 2009 - International Joint Conference on Computational Intelligence
268