HOW TO LEARN A LEARNING SYSTEM

Automatic Decomposition of a Multiclass Task with Probability Estimates

Cristina Garcia Cifuentes and Marc Sturzel

EADS Innovation Works, CTO-IW-SI-IS, 12, rue Pasteur, 92152 Suresnes, France

Keywords: Machine learning, Classification, Multiclass, Calibration, Isotonic regression, Output codes, ECOC,

coupling, Probability estimates, Logical fusion.

Abstract: Multiclass classification is the core issue of many pattern recognition tasks. In some applications, not only

the predicted class is important but also the confidence associated to the decision. This paper presents a

complete framework for multiclass classification that recovers probability estimates for each class. It

focuses on the automatic configuration of the system so that no user-provided tuning is needed. No

assumption about the nature of data or the number of classes is done either, resulting in a generic system. A

suitable decomposition of the original multiclass problem into several biclass problems is automatically

learnt from data. State-of-the-art biclass classifiers are optimized and their reliabilities are assessed and

considered in the combination of the biclass predictions. Quantitative evaluations on different datasets show

that the automatic decomposition and the reliability assessment of our system improve the classification rate

compared to other schemes, as well as it provides probability estimates of each class. Besides, it simplifies

considerably the user effort to use the framework in a specific problem, since it adapts automatically.

1 INTRODUCTION

Many supervised machine learning tasks can be

formulated as a multiclass classification problem:

object detection and recognition (e.g. for video-

surveillance), image mining and categorization (e.g.

for large database management or for intelligence

tasks), etc. In many applications not only the

performance in the classification task is important,

but also the capability of the system to recover the

posterior probabilities of each class, or at least the

ability to somehow assess the reliability of the

decision. This case appears for example in data

mining, where estimated probabilities can be used to

rank the elements of a database with regards to the

considered query. In other operational cases,

probabilities are even explicitly required by the end-

users (e.g. in order to help deciding whether or not

an alarm should be raised).

This article focuses on multiclass tasks which

represent the main issues for real-world systems.

Some machine learning models (e.g. decision trees

and neural networks) are able to naturally handle

multiple classes. Others (e.g. boosting and support-

vector machines) were conceived for distinguishing

between only two classes and their extension to

multiclass is more problematic (Allwein et al, 2000).

In such cases the multiclass problem is typically

decomposed into many biclass classification

problems which are solved separately and then

combined to make the final decision. This approach

is attractive because it enables the usage of any kind

of pre-existing classifiers which provides huge

computational enhancements when hardware

acceleration already exists, for instance on DSPs or

ASICs.

1.1 Related Work

Many possible decompositions of a k-class problem

into l binary problems have been proposed: one-

against-all, leading to k problems of discrimination

between one class and all others; all-pairs (Hastie

and Tibshirani, 1998), that compares all possible

pairs of classes, error-correcting output codes

(ECOC) (Dietterich and Bakiri, 1995), a method

which associates each class to a word of an error-

correcting code. The latter can be represented by a

coding matrix

M ∈ {−1,+1}

k×l

for some l, each row

being one word of the code and each column

inducing a biclass problem. Allwein et al (2000)

suggested a unifying generalization of all three

589

Garcia Cifuentes C. and Sturzel M. (2010).

HOW TO LEARN A LEARNING SYSTEM - Automatic Decomposition of a Multiclass Task with Probability Estimates.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 589-594

DOI: 10.5220/0002725005890594

 SciTePress

Figure 1: Example of coding matrix. The decomposition

into binary problems can be represented by a matrix

M ∈ {−1,0,+1}

k×l

, where k is the number of classes and l

the number of induced binary problems. If M(c,b) = +1,

the examples of the class c are considered to be positive

examples for the binary classification problem b. If

M(c,b) = −1, they are considered negative. If M(c,b) = 0,

the examples of class c are not used to train b.

approaches by taking the matrix from the larger set

{−1,0,+1}

k×l

(Figure1).

Since its appearance, the significance of the

coding strategy has being brought into question. The

ECOC method was originally motivated by error-

correcting principles, assuming that the learning task

can be modeled as a communication problem, in

which class information is transmitted over a

channel. From the perspective of error-correcting

theory, it is desirable that codewords are far from

each other. Allwein et al (2000) deduced a bound on

the generalization error that confirms this. However,

they noted that this may lead to difficult binary

problems. Guruswami and Sahai (1999) argued that

one reason why the powerful theorems from coding

theory cannot be directly applied to prove stronger

bounds on the performance of the ECOC approach is

that in the classification context errors made by

binary classifiers do not occur independently. Dekel

and Singer (2003) considered the fact that

predefined output codes ignore the complexity of the

induced binary problems, and proposed an approach

in which the set of classifiers and the code are found

concurrently. On our side, we still rely on the error-

correcting properties of codes, but only as a point of

departure to build our final coding matrix. As for the

issues of the correlation and the difficulty of binary

tasks, we deal with both by empirically assessing the

joint performance of the set of classifier. Thus, our

approach guarantees the choice of informative and

complementary binary classifiers.

Coupled with the issue of finding an appropriate

decomposition, the other major issue concerns the

design of a suitable combining strategy for inferring

the correct class given the set of outputs. Allwein et

al (2000) recalled Hamming decoding and proposed

loss-based decoding as an alternative for margin-

based classifiers. However, this decoding paradigm

does not deal with our aim to recover the probability

of each class.

In order to obtain probability estimates, Kong

and Dietterich (1997) and Hastie and Tibshirani

(1998) proposed combining methods for ECOC and

all-pairs respectively. Zadrozny (2001) extended the

latter to the general matrices of Allwein et al (2000).

Nevertheless, in these works the design of a code for

a given multiclass problem is not considered and the

individual biclass classifiers are assumed to return

probabilities, which is not always the case. In order

to fuse the outputs of such a set of classifiers, a

calibration is needed first, as indicated by Zadrozny

and Elkan (2002). Our framework deals with all

these issues in an efficient and generic way.

In parallel to the work on the decomposition into

binary problems, the design of a multiclass

algorithm that treats all classes simultaneously has

been addressed, among others, by Zou et al (2005).

In particular, they suggested a multiclass SVM.

However, it does not focus on discovering the

probabilities of each class. Instead, the output is a

vector of scores, which we cannot calibrate

effectively with the techniques proposed so far on

restricted databases due to the curse of

dimensionality. Besides, we prefer not being bound

to a particular classifier; indeed, our framework can

for instance exploit simultaneously SVMs and

AdaBoost classifiers: the system is free to select the

most appropriate model according to the data and its

properties.

1.2 Overview of the System

We present a multiclass classification framework

which fits automatically any multiclass classification

task, regardless of the nature and amount of data or

the number of classes. We follow the approach of

decomposing into several biclass problems and then

combining the biclass predictions. This is

qualitatively motivated by two main aspects: the aim

to recover probability estimates for each class given

limited learning data and the existence of high-

performing biclass methods.

As first main contribution, we propose a scheme

to automatically learn an appropriate decomposition

given training data and a user-defined measure of

performance (Section 2.1), which avoids too

correlated or too difficult biclass classification

problems which are maladjusted to the particular

multiclass task. The obtained biclass problems are

solved by means of state-of-the-art classifiers, which

are automatically optimized and calibrated.

Calibration (Section 2.2) allows the classifiers to

provide probability estimates, and thus makes it

possible to take into account their different

binary classifiers

classes

+1 +1 +1 +1 0 –1

0 –1 –1 +1 +1 –1

–1 +1 -1 0 –1 –1

–1 0 +1 –1 –1 +1

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

590

reliabilities in the combination step. Then, the

biclass outputs are combined into a probability

distribution among all the classes (Section 2.3).

Furthermore, our system can fuse several probability

distributions when many observations of a same

object are available. A decision can then be made

regarding the class with the highest probability, but a

further step may be done in order to get one score

per class that has better ranking properties than

individual probabilities alone: this makes the system

especially suitable for multiclass ranking tasks

(Section 2.4). Experimental results and conclusions

are presented in Sections 3 and 4.

2 TECHNICAL DETAILS

2.1 Matrix Learning

The decomposition into binary problems can be

represented by a coding matrix (Fig. 1). The number

of possible matrices explodes with the number of

classes. Considering all of them is neither possible

nor interesting. Instead, we propose a heuristic

method which is compatible with practical

constraints of computational cost and constructs a

matrix with good properties with regards to the

nature of data. More particularly, we limit our search

to a maximal number of columns, and we select

among them a subset which leads to good

performance.

We do not use a matrix which is necessarily a

strict error-correcting code. Such codes are difficult

to generate for each possible number of columns,

and the integrity and properties of the code would

not be guaranteed due to deletion of invalid or

redundant columns (e.g. a column with equal

elements, or two columns which are the logical

negative of each other). Anyway, the correcting

properties are useful only if the classifiers are

sufficiently uncorrelated, which depends not only on

the properties of the matrix but also the nature of the

data. Thus, as alternative to the matrix being exactly

a code, we rather use a code only as a base for

building the matrix. Concretely, we choose a fixed

BCH code of 32 words 15 bits long, and with

Hamming distance between words of at least 7,

which is enough for a reasonable number of classes

(for very high number of classes – in our case

greater than 32 – another code should be generated

as initialization point; an approach based on random

matrices might be computationally less expensive).

With this code and a given number of classes k, we

obtain a sufficiently large set of columns –

presumably with better correcting properties than a

random matrix – by taking all k × 1 sub-matrices as

potential columns (redundant or invalid columns are

ignored). We denote the set of columns as

{

}

1...N

(1)

Next, we want to find the optimal subset of

columns, as keeping all of them may not be the most

appropriate solution; besides we may have

constraints in the prediction time. The user may

provide a performance measure σ adapted to their

operational needs. Our target is defined as

)(

argmax

)(

℘∈

(2)

where ℘(ϑ) is the power set of ϑ.

An optimization procedure such as a genetic

algorithm is suitable to select the subset of columns,

as the search space is potentially large and many

local optima may lead to a non-convex cost function.

The evaluation of any subset is based on its

empirical performance on a validation set of data

according to the user’s criterion (e.g. related to the

global error rate; or the worst of error rates

associated to each class). In particular, all the biclass

classifiers corresponding to the maximal matrix are

trained and their predictions on the validation data

are pre-computed; any subset of columns can then

be quickly evaluated.

Once the definitive k × l coding matrix has been

determined, the corresponding classifiers can be

optimized. We choose them by means of cross-

validation among different learning algorithms (e.g.

boosting, SVM) and their respective parameters (e.g.

weak classifier or kernel type). These biclass

classifiers are then trained and calibrated. Doing this

optimization after the correcting-code selection only

marginally affects performance, but leads to reduced

computational cost: this is required from a pragmatic

point of view when large number of classes and

large databases are considered.

2.2 Calibration

Many biclass learning algorithms map the input to a

score whose sign indicates if the input has been

classified as positive or negative and whose

magnitude can be taken as a measure of confidence

in the prediction (Allwein et al, 2000; Zadrozny and

Elkan, 2002). However, the scores from different

classifiers are not directly comparable, even for

classifiers of the same kind (partial sums of boosted

classifiers, for example, have no intrinsic scale).

HOW TO LEARN A LEARNING SYSTEM - Automatic Decomposition of a Multiclass Task with Probability Estimates

591

Calibration consists in finding the mapping from raw

scores to accurate probability estimates, which are

needed when we want to combine the classification

output with other sources of information. We can

think of a score as a non-linear projection of the

example into a 1-dimensional space, which

presumably corresponds to the direction that best

discriminates between the two classes. Calibration

attempts to regain some of the lost information in

this projection.

The straightforward way of calibrating consists

in dividing the possible scores into segments and

calculating the empirical probability in each of them.

The choice of the segment sizes is a trade-off

between a sufficiently fine representation of the

mapping function and a sufficiently accurate

estimate in each interval. Zadrozny and Elkan

(2002) made a review of two methods for calibrating

two-class classifiers – Platt’s method and binning –

and introduced a method based on isotonic

regression. We avoid parametric methods (e.g.

Platt’s) as the relation between SVM scores and

empirical probabilities does not necessarily fit a

predefined function for all datasets and all learning

algorithms. Binning guarantees a minimum number

of examples in each segment, but it does not

maintain the idea of local averaging and the number

of bins has to be chosen. Isotonic calibration only

imposes the mapping to be non-decreasing, which is

an interesting way of regularizing given that scores

are supposed to be a measure of confidence in the

prediction. In our framework, isotonic regression is

preferred, because of its nice compromise between

regularity and local fitting, adapting automatically to

the training data, without additional a priori.

2.2.1 Reliability of the Probability Estimates

Obviously, the obtained mapping varies depending

on the calibration data. Moreover, we have noticed

that the reliability of the probability estimate is not

necessarily the same for all scores, as it depends on

the distribution of the data along the scores: until

now, little attention has been paid to this issue, while

it could provide more precise information for the

fusion process, and therethrough a more reliable

output. We are interested in assessing the relative

reliabilities of the probability estimates obtained

from different classifiers on the same test example,

in order to use them as weighting coefficients in the

posterior combination phase, instead of assigning a

global confidence to each classifier. Thus, each

classifier would be weighted differently according to

the test example and its ambiguity.

The length of the confidence interval of the

estimate in each score segment could be used as

basis for these coefficients. However, as each score

interval is treated independently, this strategy does

not take into account the regularization effect of

isotonic regression, by which the obtained estimates

are much less variable in practice. Furthermore, it

ignores the fact that estimates are not reliable if the

partition of the scores axis is not sufficiently fine. In

the case of isotonic calibration, this happens when

the underlying mapping is decreasing in some

interval. We have considered the analysis of score

sub-segments by means of hypothesis testing. We

look for the presence of sufficient statistical

evidence to declare that the average in the sub-

segment does not match the average in the whole

segment, and assign reliability accordingly.

Alternatively, variability can be empirically

estimated by using different subsets of the

calibration data to perform the calibration. We

propose to average the different calibrations

obtained this way to enhance the global calibration,

when a sufficient amount of calibration data is

available.

2.3 Combination Strategy

Once we have produced diverse classifiers, a

suitable combining strategy must be designed

according to two possible aims: inferring the correct

class given the set of outputs, or obtaining

probability estimates for each class. Our framework

focuses on the second case.

We consider from now on that the outputs of the

binary classifiers are probability estimates. In other

terms, for each column b of M and each example x

with class c, we have an estimate r

(x) such that

∑

∪∈

∈

∪∈

∈

NAc

NAcAcr

)|P(

),|P()(

(3)

where A and N are the sets of classes for which

M(c,b) = +1 and M(c,b) = −1 respectively. For each

example x, we want to obtain a set of probabilities

P(c = c

| x) = p

(x) compatible with the set of r

(x).

Note that if the matrix has no zero entries, the

expression reduces to

∑

∈

pAcr )( )|P()( xxx

(4)

This is an over-constrained problem which – as

recalled by Zadrozny and Elkan (2002) – can be

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

592

solved by least-squares with non-negativity

constraints or minimizing the Kullback-Leibler

divergence. We notice that both the squared error

and the Kullback-Leibler divergence may be

weighted to give more or less importance to the

match of certain classifiers. The idea is to focus on

matching the reliable observations r

, so as to

converge to the good solution even if the r

are not

compatible. Hastie and Tibshirani (1997) include the

number of examples used for training each classifier

as weights as ‘a crude way for accounting for the

different precisions in the pairwise probability

estimates’. We argue that this can be done in a finer

way, as presented in Section 2.2.

2.4 Fusion of Redundant Data and

Ranking Scores

Our system recovers probability estimates of each

class given a test example. In addition, we have

considered fusing the obtained probability

distributions when many observations of a same

object are available. A number of different

paradigms for performing data and information

fusion have been developed. They differ in the way

they represent information and more concretely in

the way they represent uncertainty (Maskell, 2008).

In this work we used the probabilistic logical

framework proposed by Piat and Meizel (1997). It

allows the combination of probability distributions

following different logical behaviors (e.g.

disjunctive) naturally handling contradictions. In

particular, both disjunctive and conjunctive

behaviors are desirable for our ranking purpose, so

we use a weighted sum of the two modes. Moreover,

we point out that these weights could be learned

statistically.

The need of a ranking score arises from the

observation that probability alone is not enough to

do an appropriate ranking when important residual

probabilities are present. We propose as score the

Euclidean distance between the observed probability

distribution and the Dirac delta distribution of the

Table 1: Performance of the tested configurations.

Area under ROC curve Error rate

satimage

(class 4)

isolet

(class 2)

satimage isolet

A 0.711 0.836 0.1095 0.0892

B 0.741 0.896 0.1095 0.0436

C 0.750 0.897 0.0890 0.0449

D 0.776 0.930 0.0870 0.0398

query class, as it introduces a penalty in ambiguous

cases. Empiric tests showed the relevance of this

measure.

3 EXPERIMENTS

We report our system’s performance on widely used

multiclass datasets with real (i.e. non-synthetic),

non-sequential data, having a reasonable dimension

(>30) and database size (>5000) compared to real-

life applications. Two datasets from the UCI

Machine Learning Repository (Asuncion and

Newman, 2007) satisfy our constraints: satimage

and isolet. The first one contains 6 classes and a test

set of 2000 elements. It has already been used in the

context of recovering multiclass probability

estimates (Zadrozny, 2001). The second one comes

from measures of spoken letters. It contains 26

classes and the test set has 1559 uniformly

distributed elements. The elevated number of classes

allows testing the scaling abilities of the system.

Besides, it has already been used in the ECOC

context (e.g. Dietterich and Bakiri, 1995).

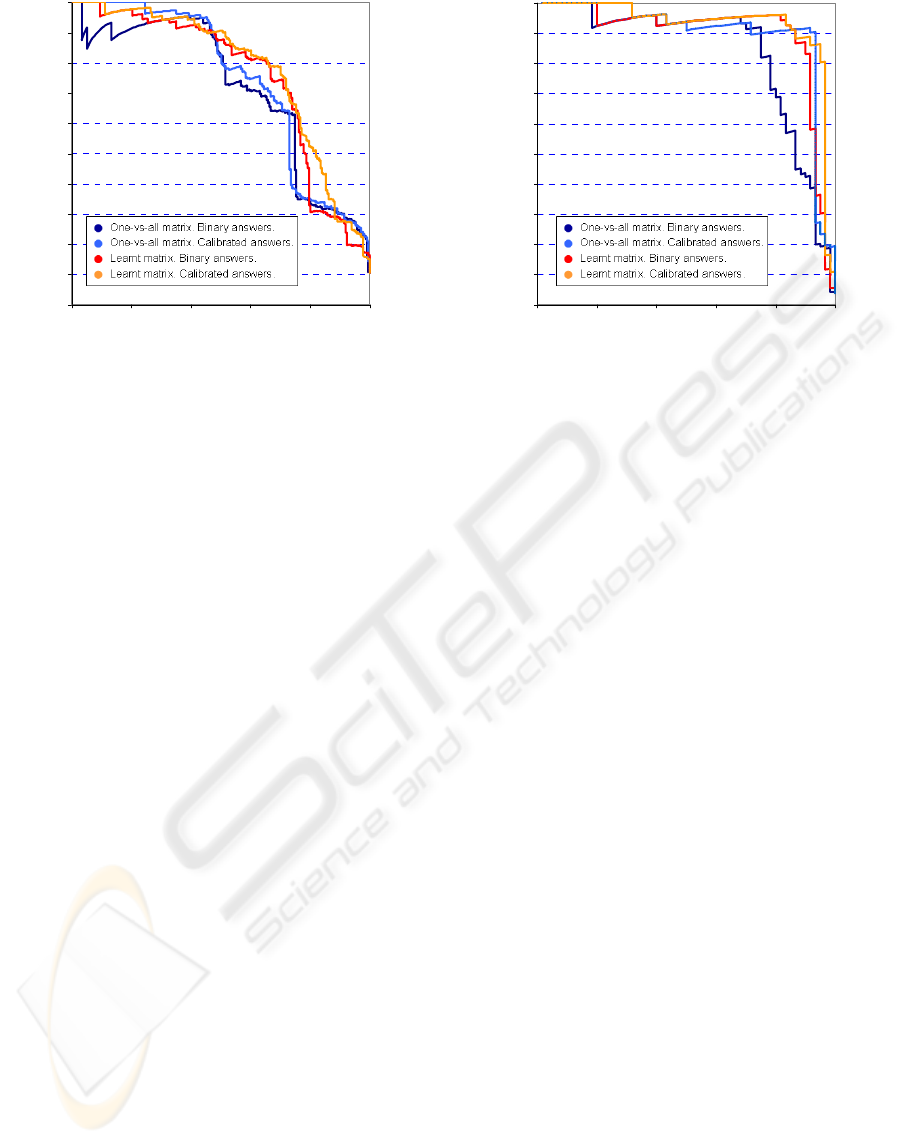
Here we compare 4 different configurations. In

the first configuration (A) we have used a one-vs-all

coding matrix and we have combined the binary

answers of the biclass classifiers directly, without

calibration. In the second (B) the one-vs-all answers

are combined after calibration. The third

configuration (C) consists of a learnt coding matrix

with biclass predictions combined without

calibration. Finally, the fourth configuration (D)

corresponds to our complete framework. We are

interested in both the classification task and the

ranking task. As a measure of performance we have

chosen the error rate in the first case and the area

under the ROC curve in the second case. The ROC

curve in the ranking task is defined by the pairs

(recall, precision) obtained at each position of the

rank. Thus, there is one ROC curve for each query.

Our ROC curves are thus different from other

benchmarks (e.g. Sebag, 2003, and Chawala, 2002).

We show only the ROC curve of the most difficult

class, but conclusions hold also for all other classes.

Table 1 and Figure 2 show the achieved results. We

can observe the improvement obtained by learning

an appropriate matrix and calibrating the biclass

outputs. In particular, we outperform the 0.1330

error rate obtained by means of a spare random

matrix on the satimage dataset (Zadrozny, 2001)

with the advantage that our resulting matrix has

much fewer columns (11 vs 64), with the consequent

gain in computational cost and prediction time.

HOW TO LEARN A LEARNING SYSTEM - Automatic Decomposition of a Multiclass Task with Probability Estimates

593

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

0 0,2 0,4 0,6 0,8 1

recall

precision

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

00,20,40,60,81

recall

precision

Figure 2: Ranking results represented by the ROC curve of the most difficult class of the dataset. On the left: the query is

class 4 (damp grey soil) from the satimage dataset. On the right: the query is class 2 (letter B) from the isolet dataset.

4 CONCLUSIONS

We have presented a multiclass classification system

which learns automatically its internal structure

according to the provided learning data; it is able to

select efficient algorithms in a pool of binary

classifiers, with an optimal choice of a relevant

coding matrix since it is computed according to the

complexity of the various binary problems. It also

provides generic and accurate calibration and results

are given as probability estimates. This system does

not need any external tuning and no user-expertise,

but just a problem-specific performance measure.

This makes it suitable and easy to use for any

multiclass task needing probability estimates or

ranking, while still successfully dealing with the

classification task, as it has proved to outperform

empirical results on two very different datasets. This

framework is also more generic and computationally

efficient than existing tools like libSVM.

REFERENCES

Allwein, E.L., Schapire, R.E., Singer, Y., 2000. Reducing

multiclass to binary: A unifying approach for margin

classifiers. Journal of Machine Learning Research,

1:113-141.

Asuncion, A. Newman, D.J., 2007. UCI Machine Learning

Repository. Irvine, CA: University of California,

[http://www.ics.uci.edu/~mlearn/MLRepository.html]

Chawala N. V., Bowyer K. W., Hall L. O., Kegelmeyer

W. P., 2002. SMOTE: Synthetic Minority Over-

sampling Technique. Journal of Artifical Intelligence

Research 16, 321-357.

Dekel, O., Singer, Y., 2003. Multiclass learning by

probabilistic embeddings. In Advances in Neural

Information Processing Systems 15, 945-952.

Dietterich, T. G., Bakiri, G., 1995. Solving multiclass lear-

ning problems via error-correcting output codes.

Journal of Artificial Intelligence Research, 2:263-286.

Guruswami, V., Sahai, A., 1999. Multiclass learning,

boosting, and error-correcting codes. In COLT '99:

Proceedings of the twelfth annual conference on

Computational learning theory, 145-155. ACM Press/

Hastie, T., Tibshirani, R., 1998. Classification by pairwise

coupling. In The Annals of Statistics, 26(2):451-471.

Kong, E. G., Dietterich, T. G., 1997. Probability estima-

tion using error-correcting output coding. In

International Conference on Artifical Intelligence and

Soft Computing.

Maskell, S., 2008. A Bayesian approach to fusing

uncertain, imprecise and conflicting information.

Information Fusion, 9(2):259-277.

Piat, E., Meizel, D., 1997. A probabilistic framework for

believes fusion. Traitement du Signal, 14(5):485-498.

Sebag, M., Azé J., Lucas N., 2003. ROC-based

Evolutionary Learning: Application to Medical Data

Mining. Artificial Evolution’03, Springer 384-396.

Zadrozny, B., 2001. Reducing multiclass to binary by

coupling probability estimates. In Advances in Neural

Information Processing Systems 14, 1041-1048.

Zadrozny, B., Elkan, C., 2002. Transforming classifier

scores into accurate multiclass probability estimates.

In KDD '02: Proceedings of the eighth ACM SIGKDD

international conference on Knowledge discovery and

data mining, 694-699.

Zou, H., Zhu, J., Hastie, T., 2005. The margin vector,

admissible loss and multi-class margin-based

classifiers. Technical report, University of Minnesota.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

594