IRREGULAR PLACEMENT PROBLEM
Solved with a 2-Level Algorithm and Collision Free Region
Andr´e Kubagawa Sato, Thiago de Castro Martins and Marcos de Sales Guerra Tsuzuki
Computational Geometry Laboratory, Mechatronics and Mechanical Systems Engineering Department
Escola Polit´ecnica da Universidade de S˜ao Paulo, S˜ao Paulo, Brazil
Keywords:
Cutting and packing, Simulated annealing, Placement problems, Optimization, Probabilistic heuristic.
Abstract:
The two-dimensional irregular open dimension packing problem is a combinatorial optimization problem that
searches a layout for a given set of irregular items within a rectangular container so that no item overlaps with
other items or protrudes from the container, where each irregular item is not necessarily convex. The container
has a fixed width, while its length can change so that all items are placed in it. The objective is to find a
layout of the set of polygons that minimizes the length of the container. The proposed algorithm construc-
tively creates layouts from an ordered list of items and a placement heuristic. The placement determines the
collision free region (represents the set of translations to create a feasible layout) for the item to be placed. It is
shown that the collision free region must be calculated using non-regularized Boolean operations, as contours
of no-fit polygons should be ignored. The proposed algorithm to solve the placement problem has two levels,
in the internal level the container has fixed dimensions, and the external level reduces or increases the variable
dimension. The placement heuristic searches for degenerated vertices and edges as they represent local max-
imum compaction. Computational comparisons on benchmark problems show that the proposed algorithm
generated highly competitive solutions. Moreover, our algorithm updated some best known results.
1 INTRODUCTION
This paper is related to the classic problem of finding
the most efficient layout for a set of irregular items
out of a givencontainer with the objective of minimiz-
ing the wasted material. There are numerous applica-
tions for this problem, including wood, textile, sheet
metal, plastics, and glass industries. W¨ascher et al.
(2007) proposed a typology that classifies the pack-
ing problems based on size, objective, assortment of
items and container type. According to this typology,
this work investigates the two-dimensional irregular
open dimension problem (ODP), in which the items
can be represented by irregular polygons and the con-
tainer is rectangular with an variable dimension. The
objective is to find the smallest container that fits all
items inside in such way that no item overlaps.
Although several strategies to search and represent
the solutions exist in the literatures, they can be di-
vided in two main categories: the first represents the
solution as an ordered list of items and applies place-
ment rules to construct a feasible layout, i. e., layouts
where no item overlaps or protrudes from the con-
tainer (Burke et al., 2007). The second considers a
feasible layout on the container and attempts to move
the items inside the container, overlapped items are
permitted, and a penalty method is used to reach fea-
sible layouts (Egeblad et al., 2007). The problem is
NP-complete (Fowler et al., 1981) and, consequently,
the searching strategies usually adopt heuristics. In
this work, a simulated annealing (SA), which was
originally proposed as an combinatorial optimization
algorithm, is used in combination with a placement
heuristic.
This work is structured as follows. Section 2 ex-
plains three basic concepts: no-fit polygon (NFP), in-
ner-fit polygon (IFP) and collision free region (CFR).
Section 3 explains that the correct and robust determi-
nation of CFRs requires non-regularized Boolean op-
erations, as contoursof NFPs should be ignored . Sec-
tion 4 presents the proposed algorithm with two lev-
els, in the internal level the container has fixed dimen-
sions, and the external level reduces or increases the
variable dimension. The placement heuristic searches
for exactly fitting positions, as they usually represent
local maximum compaction. Section 5 presents some
results and the conclusions are in section 6.
79
Kubagawa Sato A., de Castro Martins T. and de Sales Guerra Tsuzuki M..
IRREGULAR PLACEMENT PROBLEM - Solved with a 2-Level Algorithm and Collision Free Region.
DOI: 10.5220/0003521900790084
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 79-84
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

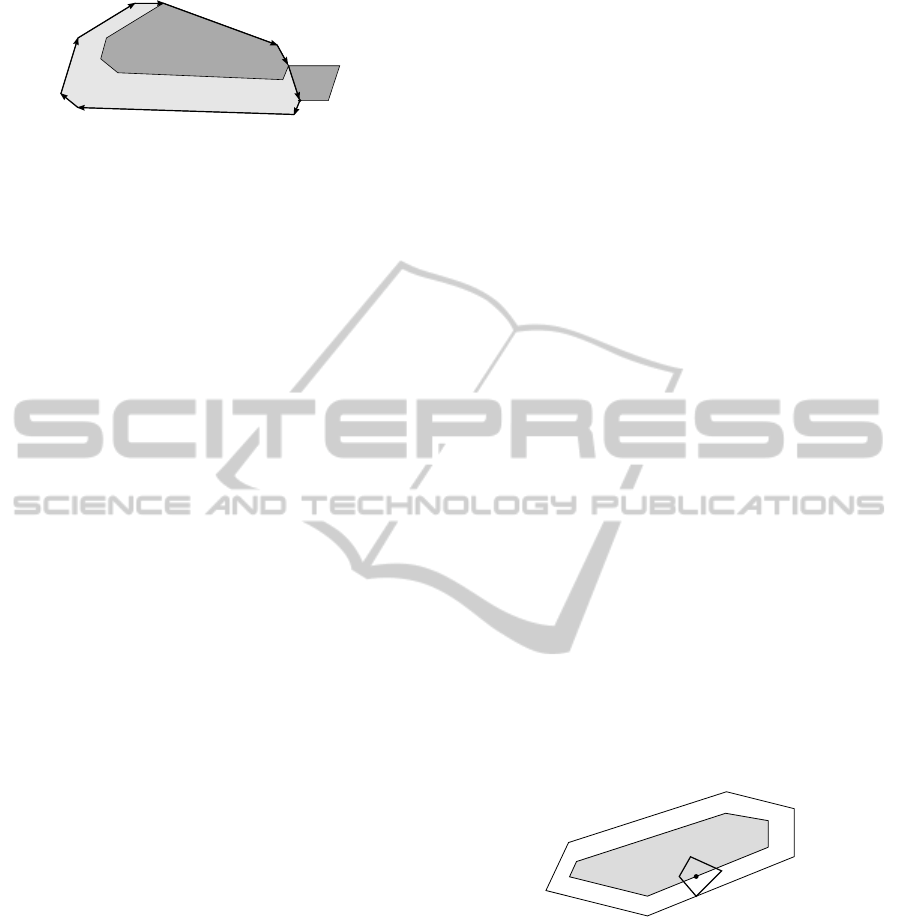
P
i
P
j
Figure 1: No-fit polygon (contour with oriented edges) in-
duced by the item P
i
to item P
j
. The reference point is the
bottom-left vertex of the item P
j
.
2 BASIC CONCEPTS
When irregular items are involved an extra dimension
of complexity is generated by the geometry. More
precisely, there is a need to determine whether two
items touch, overlap or are separated. There exists
a number of solutions to this problem ranging from
simple to complex, these include raster method, direct
trigonometry and NFP. In this work, the NFP is used
to evaluate all the feasible positions for the placement
of a new item.
The NFP alone has limited utility in cutting and
packing problems. Some recent works are using the
CFR to determine feasible layouts in containers with
fixed dimensions. Martins and Tsuzuki (2009, 2010)
proposed a constructive heuristic where the CFR rep-
resents feasible placements for a moveable item con-
sidering the already placed items and the container.
This section describes how the CFR is determined us-
ing NFPs and IFPs.
2.1 No-Fit Polygon
The NFP represents translations applied to items and
is mathematically represented by a set of vectors. It
represents the set of forbidden translations that, when
applied to a moveable item, intersects with a fixed
item. The NFP is induced by the fixed item to the
movable item. An example of a no-fit polygon is rep-
resented in Fig. 1. If the reference point is placed at
the interior of the NFP then the moveable item col-
lides with the fixed item. On the other hand, if the
reference point is placed at the boundary of the NFP
then the moveable and fixed items touch. For an item
P, let i(P) be its interior, ∂P be its boundary and c(P)
be its complement.
Definition 2.1. Consider the fixed item P
i
and the
moveable item P
j
. The NFP induced by item P
i
to
item P
j
, denoted by ϒ(P
i
,P
j
), is the set of translation
vectors applied to P
j
that leads it to a collision with
P
i
. Thus,
ϒ(P
i
,P
j
) = i(P
i
) ⊖ i(P
j
) (1)
=

~
v|∃a ∈ i(P
j
),a+
~
v ∈ i(P
i
)

.
Numerous algorithms to determine the NFP were
proposed. Mahadevan (1984) developed an algorithm
based on a sliding scheme. However, more efficient
algorithms based on Minkowski sums exist (Burke
et al., 2007; Bennell and Song, 2008). It is possi-
ble to obtain the NFPs using Minkowski sums and the
opposed polygon.
Definition 2.2. The Minkowski sum of two polygons
P
i
and P
j
, noted P
i
⊕ P
j
, is defined as the set of points

O+
~
v+
~
w|O+
~
v ∈ P
i
,O+
~
w ∈ P
j

.
Definition 2.3. The opposed polygon for a given
polygon P
j
, denoted by −P
j
, is defined as the set of
points −P
j
=

O−
~
w|O+
~
w ∈ P
j

.
From the above definitions, one can see that
i(P
i
) ⊖ i(P
j
) = i(P
i
) ⊕ (−i(P
j
)) (2)
meaning that the NFP is produced by the Minkowski
sum of the fixed item with the opposed item to be
placed. This algorithm is very efficient for convex
polygons. The result of a Minkowski sum of two
convex polygons is a convex polygon built from the
original polygons edges ordered counterclockwise.
Non-convex polygons can be decomposed into con-
vex polygons, as the applied transformations (rotation
and translation) do not affect such decomposition.
2.2 Inner-Fit Polygon
The IFP is a concept derived from the NFP and it rep-
resents the set of translations that places an item in-
side a container (Dowsland et al., 2002). The IFP can
be obtained by sliding the item along the internal con-
tour of the container. (see Fig. 2).
Figure 2: Inner-fit polygon (gray polygon) induced by con-
tainer to item.
Definition 2.4. The IFP induced by container C to
item P
j
, denoted by Λ(C ,P
j
), is the set of translation
vectors applied to P
j
that leads it to be inside the con-
tainer. Thus,
Λ(C ,P
j
) = c(c(C ) ⊕ (−i(P
j
))) (3)
=

~
v|∀a ∈ i(P
j
),a+
~
v ∈ C

.
2.3 Collision Free Region
Consider a container C and a set of placed items
P = {P
1
,··· ,P
n
}, with no collision and totally inside
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
80

the container. A new item P
m
, m > n will be placed
in the container, keeping the layout feasible, i.e. no
items collide or protrude from the container. The CFR
represents such a set of translations for item P
m
(see
Fig. 3).
Definition 2.5. The CFR is the set of all translations,
that, when applied to a specific item, place this item
in the interior of the container without colliding with
the already placed items.
Figure 3: The CFR is filled with a hatch pattern. The item
to be placed is not filled and the already placed items are
filled with gray.
When there are no placed items, the CFR is the
IFP. The first step to determine the CFR is to obtain
the corresponding IFP. The next step is to subtract the
NFPs induced by the placed items. The CFR, denoted
Π(C ,P ,P
m
), can be determined using the expression:
Π(C ,P ,P
m
) = Λ(C ,P
m
) −
[
P
i
∈P
i(P
i
) ⊖ i(P
m
). (4)
3 NON-REGULARIZED
BOOLEAN OPERATIONS
As shownin the previoussection, the determination of
the CFR requires the use of Boolean operations over
polygons. However, those Boolean operations can-
not be regularized as they assume that a polygon con-
tains its boundary. The CFR is determined through
Boolean operations applied to NFPs and IFPs. As
NFPs represent forbidden translations, their bound-
aries represent allowable translations. The NFP’s
boundaries represent translations that place the move-
able item touching the fixed item, which is not for-
bidden. Then, for the determination of the CFR, it is
necessary to use non-regularized Boolean operations.
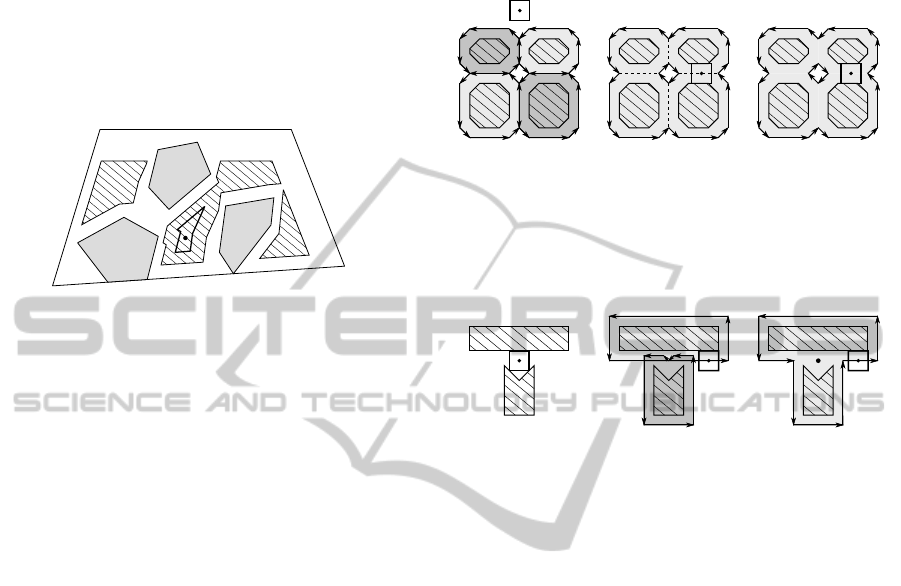
Fig. 4 shows an example where four items are al-
ready placed and the moveable item can be placed be-
tween the already placed items. The reference point
of the moveable item can be placed at the common
boundaries of the original NFPs shown in Fig. 4.(a).
The union of all NFPs must result in a polygon
with internal edges (degenerated edges) as shown in
Fig. 4.(b). However, when regularized Boolean oper-
ations are used, the final result is shown in Fig. 4.(c)
without the internal edges. Fig. 5 shows a similar sit-
uation where the the union of all original NFPs must
result in a polygon with one internal vertex (degener-
ated vertex).
(a) (b) (c)
Figure 4: (a) On top, the moveable item with a central ref-
erence point. On the bottom, four fixed items (filled with a
hatch pattern) and the four induced NFPs represented by its
oriented contours. (b) CFR, with its four degenerated edges
shown (dashed lines). (c) Result of the regularized union of
all the NFPs, which does not have degenerated edges.
(a) (b) (c)
Figure 5: (a) Desired placement of a rectangular item with
a central reference point. Fixed items are represented by
hatched polygons. (b) The two NFPs represented by its ori-
ented contours. (c) CFR, with its degenerated vertex shown
(internal vertex).
The result of non-regularized Boolean operation
may have edges or vertices that do not belong to the
boundary. They are called degenerated edges and de-
generated vertices. When not specified, the edges or
vertices are part of the contour. When moveable items
are placed on degenerated vertices or edges usually
implies in a more compact layout. This affirmation is
discussed in subsection 4.1.
In this work, new non-regularized Boolean opera-
tions were developed. Generally, regularized Boolean
operations are implemented in three steps (Vatti,
1992): edge intersection determination, edge and con-
tour labeling and edge and contour collection. The
new algorithm developed in this work has the same
three steps, and the main differences are in edge
and contour labeling and edge and contour collection.
They are associated with the creation and collection of
degenerated edges and vertices. As equation (4) uses
exclusively unions and subtractions, the intersection
was not implemented. Degenerated edges and ver-
tices are created in situations where they exist in the
results but not in the input polygons, as can be seen
on Fig. 6 (union) and Fig. 7 (subtraction). The collec-
tion of degenerated edges and vertices is a decision
to maintain or eliminate them. The developed algo-
IRREGULAR PLACEMENT PROBLEM - Solved with a 2-Level Algorithm and Collision Free Region
81

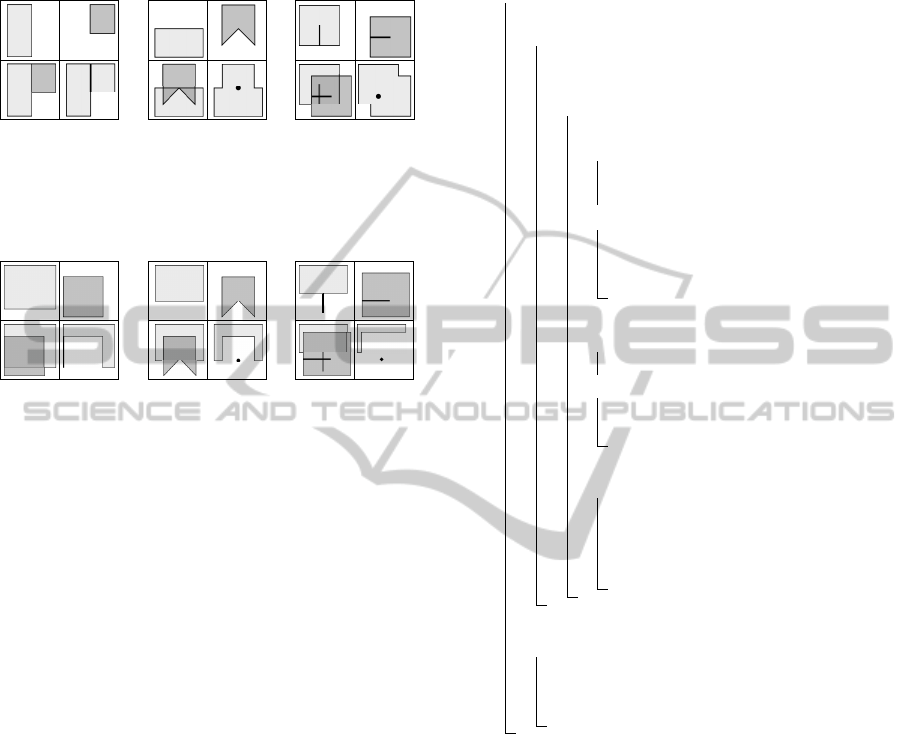
rithm consists of a robust implementation, high per-
formance and works with finite precision (Sato et al.,
2010).
(a) (b) (c)
Figure 6: Three cases of degenerated elements generation
for non-regularized Boolean union operation. Consider A∪
B operation. Top left: polygon A. Top right: polygon B.
Bottom left: superposition. Bottom right: result.
(a) (b) (c)
Figure 7: Three cases of degenerated elements generation
for non-regularized Boolean subtraction operation. Con-
sider A−B operation. Top left: polygon A. Top right: poly-
gon B. Bottom left: superposition. Bottom right: result.
4 PROPOSED APPROACH
The proposed algorithm searches for layouts for a
given set of irregular items out of a given rectangu-
lar container with an open dimension such that this
dimension is minimized. Each irregular item can be
rotated by a finite set of angles. The irregular items
can be any polygon, convex or non-convex and may
contain holes.
To solve this problem, a two level algorithm was
developed (see Fig. 8). The internal level considers
the container with fixed dimension. SA is used to
control the sequence, orientation and position of each
item. The objectivefunction is the wasted space of the
container. The global convergence condition happens
when, for a given temperature, the wasted space of the
container is exactly the same in all tries and they are
equal to the best already found wasted value. The lo-
cal convergence condition is a predefined maximum
number of iterations. When considering a container
width fixed dimensions, the wasted space can only as-
sume a set of discrete values (Martins and Tsuzuki,
2009, 2010).
The external level controls the value of the open
dimension and the initial temperature of the SA. Once
the internal level ends, a feasible layout with all irreg-
ular items placed is found, the external level shrinks
x ← <Initial random solution>
T
0
← <Initial temperature>
L ← <Initial container dimension>
while <Not finished> do
while <Global stop condition not
satisfied> do
T
i
← T
i
∗ α; i ← i+ 1
while <Local stop condition not
satisfied> do
val ← random(0,1)
if val < 0.5 then
x
∗
←<Modify placement
sequence>
else
<Select the movable item>
x
∗
←<Select a vertex using
adopted placement heuristic>
∆E = F(x
∗
) − F(x)
if ∆E < 0 then
x ← x
∗
else
if random(0,1) < e
−∆E/kT
then
x ← x
∗
if <All items are placed inside the
container> then
L ← (1− p
dec
)L
<Container dimension>← L
<Global and local stop
condition satisfied>
if <At least one of the items is not placed
inside the container> then
L ← (1+ p
inc
)L
<Container dimension>← L
i ← 0; T
0
← <Initial temperature>
Figure 8: Proposed Algorithm.
the container and resets the SA. When no solution
with all items placed is found, the open dimension
of the container is increased and the internal level is
restarted. For the external level, two parameters p
dec
and p
inc
are used to control, respectively, the shrink-
age and expansion of the container.
4.1 Placement Heuristic
In this work, a placement heuristic that gives priority
to exactly fitting position is used. When an exactly fit-
ting placement exists then the moveable item touches
the fixed item in at least two different locations. The
placement of a new item in a exactly fitting position
often represents a local compaction. The main moti-
vation of this work is that degenerated edges and ver-
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
82

tices represent exactly fitting positions. In the pro-
posed algorithm, placement in these situations have
higher priority. Another placement heuristic of inter-
est is at convex vertices from the CFR. Fig. 9 shows
examples of moveable items placed at convex ver-
tices.
(a) (b) (c)
Figure 9: Placement on a concave vertex of the CFR. Fixed
items are represented by polygons filed with hatch pattern
and the movable item by a gray filled polygon.
The placement always occurs at vertices from
the CFR. Previous works showed that this placement
helps the algorithm finding a solution in smaller time
without compromising the quality of the final solu-
tion. However, there are special cases where the algo-
rithm is not capable to find the optimal solution just
by placing new items exclusively at CFR’s vertices.
The adopted placement heuristics have the follow-
ing order of priority: degenerated vertex, degenerated
edge, convex contour vertex. If the CFR has more
than one degenerated vertex, the algorithm chooses
one randomly. If no degenerated vertex are found,
then the placement should occur in one degenerated
edge’s vertex, randomly chosen. If no degenerated el-
ements exists, one convex vertex from the boundary
randomly chosen is selected, with no priority order.
The proposed algorithm is shown in Fig. 8.
5 RESULTS
The proposed algorithm was tested with 13 bench-
mark data sets, found on ESICUP’s (EURO Spe-
cial Interest Group on Cutting and Packing) website
1
.
These sets are irregular strip packing problems with
the objectiveof minimizing the length of the container
with a fixed width. The objective was to find the min-
imum length for the container such that all items fit
inside the container and they do not overlap. The ir-
regular items have up to four possible orientations(0
◦
,
90
◦
, 180
◦
or 270
◦
). All tests were executed on a i7
860 processor with 4GB RAM.
The adopted external level parameters p
dec
and
p
inc
were 1% e 0,3% respectively. Table 1 shows the
minimum length and the density of the most compact
1
http://paginas.fe.up.pt/˜esicup/tiki-index.php.
layout found by the algorithm. Fig. 10 show the op-
timal layouts found by the proposed algorithm. The
Albano, Jakobs and Marques layouts found are the
best results published in the literature. As for the
Jakobs1 set, it has the same density as the one pub-
lished by (Egeblad et al., 2007). The algorithm was
also capable of achieving 100% density for the prob-
lems Dighe1 and Dighe2.
Table 1: Results from Benchmark Data Sets. Minimum
length and density (%) are specified.. I: (Imamichi et al.,
2009). B: (Bennell and Song, 2008). E: (Egeblad et al.,
2007) G: (Gomes and Oliveira, 2006). The data sets with
∗
are the best results in the literature.
Case Proposed Best
Alb 9848.72 (88.39)
∗
9905.94 (88.16) (I)
Da 57.82 (87.71) 57.63 (87.87)
∗
(B)
D1 1000 (100)
∗
1000.00 (100)
∗
(BG)
D2 1000 (100)
∗
1000.00 (100)
∗
(BG)
Fu 30.99 (91.96) 30.97 (92.03)
∗
(E)
J1 11.00 (89.07)
∗
11.00 (89.07)
∗
(E)
J2 22.75 (84.83)
∗
23.39 (82.51) (I)
Mao 1753.20 (84.07) 1731.26 (85.15)
∗
(E)
Mar 76.85 (90.01)
∗
77.04 (89.82) (E)
S0 59.03 (67.59) 58.30 (68.44)
∗
(E)
S1 55.51 (71.88) 54.04 (73.84)
∗
(EI)
S2 25.93 (83.30) 25.64 (84.25)
∗
(I)
Sh 61.65 (87.59) 60.18 (89.69)
∗
(B)
Tr 241.83 (90.07) 241.23 (90.46)
∗
(E)
6 CONCLUSIONS
Using the proposed non regularized Boolean opera-
tions algorithm, it was possible to determine degener-
ated edges and vertices. A new placement heuristic
was proposed considering the importance of place-
ment at degenerated elements. A two-level algorithm
was proposed to solve the open dimension problem.
The results from the benchmark data sets from liter-
ature showed to be very competitive, finding in some
cases the best result in the literature.
The proposed algorithm has two parameters: the
ratio by which the container is shortened, and the ra-
tio by which the container is increased. The tests were
conducted using constant ratios. However, we think
that it is possible to control the ratios through an al-
gorithm. This was left as future work.
ACKNOWLEDGEMENTS
Andr´e Kubagawa Sato was supported by CNPq.
Thiago Castro Martins was supported by FAPESP
IRREGULAR PLACEMENT PROBLEM - Solved with a 2-Level Algorithm and Collision Free Region
83

(a)
(b)
(c) (d) (e)
(f) (g) (h)
(i) (j) (k)
(l) (m) (n)
Figure 10: The best solutions obtained by the proposed al-
gorithm. (a) albano. (b) shapes0. (c) dagli. (d) fu. (e)
dighe1. (f) dighe2. (g) mao. (h) marques. (i) shapes1. (j)
shapes2. (k) shirts. (l) trousers. (m) jakobs1. (n) jakobs2.
(Grant 2009/14699–0). Marcos Sales Guerra Tsuzuki
was partially supported by the CNPq (Grants
304.258/2007–5 and 309.570/2010–7). This research
was supported by FAPESP (Grants 2008/13127–2and
2010/18913–4).
REFERENCES
Bennell, J. A. and Song, X. (2008). A comprehensive and
robust procedure for obtaining the no-fit polygon us-
ing minkowski sums. Eur J Oper Res, 35:267–281.
Burke, E. K., Hellier, R. S. R., Kendall, G., and Whitwell,
G. (2007). Complete and robust no–fit polygon gen-
eration for the irregular stock cutting problem. Eur J
Oper Res, 179:27–49.
Dowsland, K. A., Vaid, S., and Dowsland, B. W. (2002). An
algorithm for polygon placement using a bottom–left
strategy. Eur J Oper Res, 141:371–381.
Egeblad, J., Nielsen, B. K., and Odgaard, A. (2007). Fast
neighborhood search for two- and three–dimensional
nesting problems. Eur J Oper Res, 183:1249–1266.
Fowler, R. J., Paterson, M., and Tanimoto, S. L. (1981).
Optimal packing and covering in the plane are np-
complete. Inform Process Lett, 12(3):133–137.
Gomes, A. M. and Oliveira, J. F. (2006). Solving irreg-
ular strip packing problems by hybridising simulated
annealing and linear programming. Eur J Oper Res,
171:811–829.
Imamichi, T., Yagiura, M., and Nagamochi, H. (2009).
An iterated local search algorithm based on nonlinear
programming for the irregular strip packing problem.
Discrete Optim, 6:345–361.
Mahadevan, A. (1984). Optimization in computer-aided
pattern packing (marking, envelopes). PhD thesis,
North Carolina State University.
Martins, T. C. and Tsuzuki, M. S. G. (2009). Placement over
containers with fixed dimensions solved with adaptive
neighborhood simulated annealing. B Pol Acad Sci
Techn Sci, 57:273–280.
Martins, T. C. and Tsuzuki, M. S. G. (2010). Simulated an-
nealing applied to the irregular rotational placement of
shapes over containers with fixed dimensions. Expert
Syst Appl, 37:1955–1972.
Sato, A. K., Takimoto, R. Y., Martins, T. C., and Tsuzuki,
M. S. G. (2010). Translational placement using simu-
lated annealing and collision free region with parallel
processing. Proc 9th IEEE/IAS INDUSCON.
Vatti, B. R. (1992). A generic solution to polygon clipping.
CACM, 35:56–63.
W¨ascher, G., Haussner, H., and Schumann, H. (2007). An
improved typology of cutting and packing problems.
Eur J Oper Res, 183:1109–1130.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
84