
Supplier Selection Using Fuzzy Linear Programming Technique for
Multidimensional Analysis of Preference (LINMAP)
Ali İhsan Boyacı, Tuğçen Hatipoğlu and Hatice Esen
Department of Industrial Engineering, Kocaeli University, Umuttepe, Kocaeli, Turkey
Keywords: Supplier Selection, Multicriteria Decision Making, Fuzzy LINMAP.
Abstract: The increasing competition forces companies to use the capital more effectively and using suppliers which
operate cheaper and with higher quality. Due to that, it is crucial to select the right suppliers. Supplier
selection is a decision making problem that involves quantitative and non-quantitative, conflicting criteria.
In The Linear Programming Technique for Multidimensional Analysis of Preference (LINMAP), all the
decision data are known precisely or given as crisp values. But the uncertainty in the real life problems
makes decision making more difficult. İn these situations, the complex situation varying with respect to
decision makers can be solved by Fuzzy logic. Because of that, Fuzzy LINMAP has been used to solve the
problem. The main aim of this study is to provide an analytical approach to decision makers for them to
make objective decisions. Thus, supplier alternatives and selection criteria are determined. And a fuzzy
LINMAP model is developed for supplier evaluation and selection of a company in automotive sector.
1 INTRODUCTION
The quality of goods and performance of
organizations and supply chains are affected heavily
by the Supplier Selection (SS), one of the most
important activities of acquisition. In supply chain
management, supplier selection problems have been
extensively studied . Since the real-life supplier
selection problems often involve multiple different
types of attributes (orindices, factors) such as
development capability, product quality,
technological level and delivery time as well price,
they may be ascribed to a kind of multi-attribute
decision making (MADM) problems (Wan and Li,
2013). A strong relationship with the suppliers can
be constructed by evaluating them through SS.
Actually, the initial set of suppliers can be reduced
to a final set by supplier selection decision process.
One of the most important steps in the selection
process is the formulation of selection criteria. There
are several descriptive studies that tried to define
criteria used by companies to select suppliers.
Dickson found in his study that quality, delivery and
performance history are the most important criteria
(Junior et al., 2013). It is difficult to make a
compromise between quality and delivery related
criteria with the purchasing functions that only
consider cost minimization objective. But in these
days, quality and delivery related criteria are gaining
more importance in the purchasing decisions. Lot-
sizing and total logistics course are affected a lot by
suppliers’ quality and delivery performance
(Choudhary and Shankar, 2014).
While taking a decision about suppliers, both
quantitative and qualitative criteria are important.
Depending on the current situation, new suppliers or
some of the current suppliers should be selected. In
either case, decision process is uncertain, caused by
subjective evaluation of criteria, multiple
stakeholders and unavailability of previous data
(Junior et al., 2014).
Supplier selection methods into two clusters of
single model and combined models are illustrated in
Fig. 1.
Besides, because the formulation of the decision
making process isn’t required in Artificial
Intelligence based models, they are gaining more
popularity. The complexity and uncertainty is better
coped in these models. Only performance on the
criteria is needed when the models are employed.
Furthermore, AI models can do actual trade-off by
using what they have learned from experts or cases
(Guo and Shi, 2014)
Due to the uncertainty in the evaluation of
qualitative criteria and weighing of different criteria
by different stakeholders, supplier selection decision
119
Boyacı A., Hatipo
˘
glu T. and Esen H..
Supplier Selection Using Fuzzy Linear Programming Technique for Multidimensional Analysis of Preference (LINMAP).
DOI: 10.5220/0005076601190126
In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 119-126
ISBN: 978-989-758-053-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
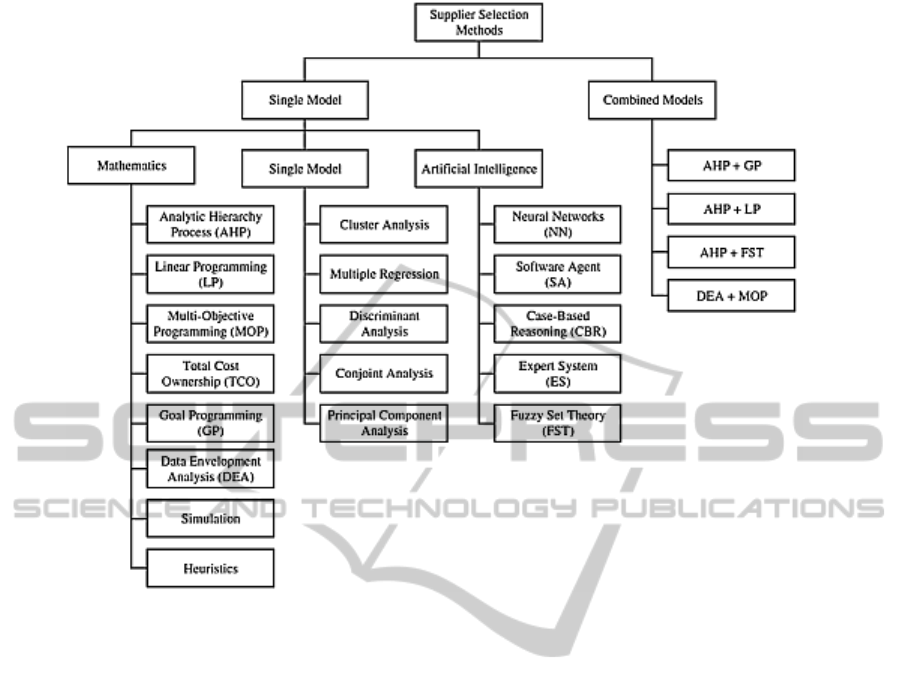
Figure 1: Existing analytical methods for supplier selection (Kannan et al., 2013).
also comprises of uncertainty. To handle the
uncertainty in the supplier selection decision
process, fuzzy set theory is one of the most
important methods. By using this method, inexact
criterion can be dealt and also qualitative and
quantitative criterion can be integrated (Junior et al.,
2013).
In multiple attribute decision-making problems,
the decisionmaker’s preference information is used
to rank alternatives. Most multiple attribute decision
making (MADM) problems include both
quantitative and qualitative attributes that use
imprecise data and human judgments (Bereketli et
al., 2011)
The purpose of using Fuzzy LINMAP in
the paper is twofold: to deal with the uncertain and
imprecise judgment of decision makers, and to
express it by fuzzy numbers. Secondly, the linear
programming technique for multidimensional
analysis of preference (LINMAP) is one of the well-
known methods for multiple attribute group decision
making (MAGDM). To validate the effectiveness of
the methodology, Bereketli et al. (2011), Chen
(2013),Wan and Li (2013), Li and Wan (2013)
found supportive and reasonable results using Fuzzy
LINMAP.
In the LINMAP method, pairwise comparisons
of alternatives given by the decision maker are
evaluated and the best alternative that has the
shortest distance to fuzzy positive ideal solution
(FPIS) is selected. In this method, the whole
decision data are known for certain or they are given
as crisp values. But, crisp data is incorrect or
insufficient to model real-life decision problems.
Actually, because human judgments are unclear and
fuzzy in nature, precise numerical values may not
represent them accurately. Instead, to model human
judgments, linguistic variables can be used (Xia et
al., 2006).
In the second half of the study, detailed
information about Fuzzy LINMAP is given. A
numerical example is given to clarify the main
results developed in Section 3. The fourth section of
the study comprises of the application results.
2 FUZZY LINMAP MODEL
2.1 Concepts and Notations of
Triangular Fuzzy Numbers
Triangular fuzzy numbers (TFNs) are a subset of
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
120
fuzzy sets with properties that make them well
suited for modelling and design-type activities.
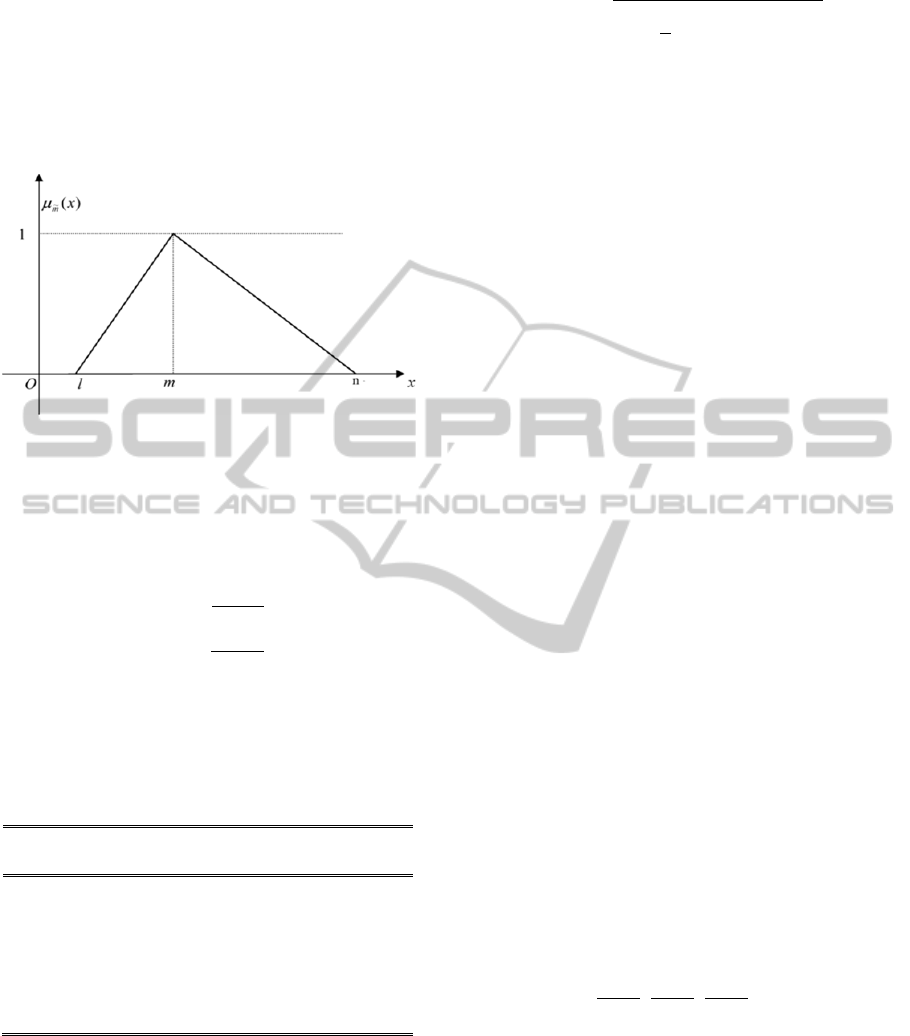
Specifically, a TFN has a triangular shape
represented by the triple (l, m, n).
Fuzzy number is known as the triangular fuzzy
number since its membership function has a
triangular form as shown in Fig 2.
Figure 2: A triangular fuzzy number.
This particular fuzzy number is widely used in both
research and practice. With the mode, left endpoint,
and right endpoint denoted by m, a, and b
respectively, the triangular fuzzy number is defined
as
;;;
1
,,
1
,
0,.
The triangular fuzzy conversion scale, given in
Table 1, is used in the evaluation model of this
paper.
Table 1: Triangular fuzzy conversion scale.
Linguistic
expression
Crisp number
value
Fuzzy number
value
Very good 5 (0.4, 0.5, 0.6)
Good 4 (0.3, 0.4, 0.5)
Medium 3 (0.2, 0.3, 0.4)
Poor 2 (0.1, 0.2, 0.3)
Very Poor 1 (0, 0.1, 0.2)
2.2 Distance between Two Triangular
Fuzzy Numbers
Let
,
,
and
,
,
be two
triangular fuzzy numbers. Then the distance between
them using vertex method which is used in this
paper can be calculated as
,
1
3
(1)
Two triangular fuzzy numbers and are
identical if and only if
,
0.
If both and are real numbers, then the
distance measurement
,
is identical to
Euclidean distance.
2.3 The Normalization Method
In this paper we discuss a fuzzy multiattribute
decision making problem which can be expressed as
follows.
Suppose there exist n possible alternatives
x
,x
,…,x
from which the decision maker has to
choose based on m attributes
,
,…,
which are
qualitative (Li and Yang, 2004). Suppose that the
rating of alternative x
1,2,…, on attribute
1,2,…, given by the decision maker is a
triangular fuzzy number
,
,
.
Hence a fuzzy multiattribute decision making
problem can be concisely expressed in matrix format
as follows:
x
…
∗
⋯
⋯
⋮⋮⋱⋮
⋯
which is referred to as a fuzzy decision matrix.
Since the physical dimensions and measurements
of the m attributes are different, so the fuzzy
decision matrix
needs to be normalized. In this
paper, we choose the following normalization
formula,
̃
,
,
⋏1
(2)
where
max
⎸
,
,
,
1,2,….,
(3)
max
⎸
,
,
,
1,2,…,
(4)
and
SupplierSelectionUsingFuzzyLinearProgrammingTechniqueforMultidimensionalAnalysisofPreference(LINMAP)
121

max
⎸
,
,
,
1,2,….,
(5)
Each ̃
0,1 obtained from above equations is
a normalized triangular fuzzy number where
̃
,
,
for any
1,2,..,and1,2,..., . Using above
equations, fuzzy decision matrix (
) can be
transformed into the following normalized fuzzy
decision matrix.
x
…
̃
∗
̃
̃
⋯̃
̃
̃
⋯̃
⋮⋮⋱⋮
̃
̃
⋯̃
2.4 Consistency and Inconsistency
Measurements
Let
̃
,̃
,…,̃
be normalized triangular
fuzzy number vector for n alternatives
1,2,…, where
arealternatives
Let the fuzzy ideal solution be
∗
∗
,
∗
,..,
∗
which is unknown a priori and must
be determined where
∗
∗
,
∗
,
∗
1,2,,,, is a positive triangular fuzzy number for
attribute
.
The square of the weighted Euclidean distance
between the alternative
̃
,̃
,…,̃
and
the FPIS
∗
∗
,
∗
,..,
∗
can be calculated as:
̃
,
∗
(6)
Using Eq. (1), we get
3
∗
∗
∗
∗
∗
(7)
In the same manner the square of the weighted
Euclidean distance between the alternative
or
̃
,̃
,…,̃
and the FPIS can be
calculated as
3
∗
∗
∗
∗
∗
(8)
Assume that the decision maker gives his
preference relations between alternatives by
,
⎸
,1,2,…, from his
knowledge and experience where the symbol is a
preference relation given by the decision maker. In
this set,
means that decision maker prefers
the alternative
to
. If the fuzy positive ideal
solution
∗
∗
,
∗
,..,
∗
and weight vector
,
,…,
are already chosen by the
decision maker, using Eq. (7) the decision maker can
calculate the square of the weighted Euclidean
distance between each pair of alternatives
,
and the fuzy positive ideal solution
∗
∗
,
∗
,..,
∗
as follows:
̃
,
∗
and
̃
,
∗
If
, then the alternative
is closer to the
FPIS than the alternative
for each of alternatives
,
∈. So the ranking order of alternatives
and
determined by
and
based on ,
∗
is consistent with the preferances given by the
decision maker. Conversely, if
, then the
,
∗
is not chosen properly since it result in that
the ranking order of alternatives
and
determined by
and
based on ,
∗
is
inconsistent with the preferences given by the
decision maker. Therefore,
,
∗
should be chosen
so that the ranking order of alternatives
and
determined by
and
based on ,
∗
is
consistent with the preferences given by the decision
maker.
An index
to measure inconsistency
between the ranking order of alternatives
determined by
and the preferences given by
the decision maker preferring
to
can be defined
as follows.
,
0
,
(9)
Obviously, if
, the ranking order of
alternatives
and
determined by
and
based on ,
∗
is consistent with the preferances
given by the decision maker. Then the inconsistency
index is defined to be 0. On the other hand, if
, the ranking order of alternatives
and
determined by
and
based on ,
∗
is
inconsistent with the preferences given by the
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
122

decision maker. Then the inconsistency index is
defined to be
. From all of these, the
inconsistency index can be rewrite as;
max0,
(10)
Using Eq.(10) we can defined total inconsistency
index of decision maker as;
,∈
max0,
,∈
(11)
In the same manner an index
can be
defined to measure consistency between the ranking
order of the alternatives
and
determined by
and
based on ,
∗
and the preferances given
by the decision maker preferring
to
as follows;
,
0
,
(12)
The equation (10) which is written for
inconsistency can be written for consistency as;
max0,
(13)
Using Eq.(10) we can defined total inconsistency
index of decision maker as;
,
∈
max0,
,
∈
(14)
2.5 Fuzzy LINMAP Model Based on
Consistency and Inconsistency
Indices
For ranking alternatives, it is necessary to
know,
∗
, and to determine
,
∗
. Because of
this, the following mathematical programming
model is constructed as follows;
Max G
G – B h
1
1,2,…,
(15)
where 0 is given by the decision maker a priori
and 0 is sufficiently small. 0 is written in
the model for ensuring that the weights generated
are not zero as it may be the case in the LINMAP
method (Srinivasan, 1973 ). The objective of the
Eq. (14) is to maximize the total consistency index
of the decision maker under the condition in which
the total consistency index is greater than the total
inconsistency index B by given value h > 0.
Combining Eqs. (11) - (14),
,∈
,∈
,∈
,∈
(16)
Using Eqs. (14) - (16) in the Eq. (15), the new model
can be written as;
maxmax0,
,∈
,
,∈
1
1,2,…,
(17)
Let
max0,
, for each pair of
,∈ then, for each ,∈
0
and
Thus, the above equation (17) can be
transformed into the following mathematical
programming model
max
,∈
,
,∈
1
1,2,…,
0 ,
∈
0 ,
∈
(18)
The
,
and
can be written explicitly
using Eqs. (7) – (8) as;
SupplierSelectionUsingFuzzyLinearProgrammingTechniqueforMultidimensionalAnalysisofPreference(LINMAP)
123

∗
∗
∗
∗
∗
3
∗
2
∗
∗
∗
2
∗
2
2
∗
2
∗
2
∗
∗
2
∗
∗
∗
2
∗
2
2
∗
2
∗
2
∗
∗
2
∗
3
∗
∗
∗
∗
∗
3
∗
2
∗
∗
∗
2
∗
2
2
∗
2
∗
2
∗
∗
2
∗
∗
∗
2
∗
2
2
∗
2
∗
2
∗
∗
2
∗
3
3
2
3
3
2
3
2
3
2
2
2
2
19
Combining Eqs.(18) and (19), we constructed the
following linear programming model:
max
,
∈
3
,
∈
2
3
2
2
6
,
∈
6
,
∈
6
,
∈
6
,
∈
3
3
2
3
2
2
6
6
6
6
3
0∀
,
∈
1
1,2,…,
0,
0,
01,2,…,
0 ,∈ (20)
where
∗
,
∗
,
∗
(21)
,
,
and
can be obtained by solving
the above linear programming (20) using simplex
method. Then the best values of
∗
,
∗
,
∗
are
calculated using Eq. (21) and which are denoted as
the triangular fuzzy numbers.
∗
∗
,
∗
,
∗
1,2,,,,
Therefore the ranking order of the alternative set
,
,...,
is generated based on the
increasing order of distances
1,2,…,
calculated using Eq. (1).
3 AN APPLICATION OF FUZZY
LINMAP ON A REAL LIFE
SUPPLIER SELECTION
PROBLEM
This application is made to solve supplier selection
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
124

problem of a company which is operating in
automotive supply industry in Kocaeli, Turkey. A
fuzzy LINMAP model is developed for this supplier
evaluation and selection problem. In the model, to
evaluate the alternative supplier which are
represented as
,
,
,
,
, four criteria is
used which are cost (
), technical (
), delivery
(
) and quality (
). These criteria are expressed
with fuzzy triangular numbers using linguistic
variables. The preferences of the purchasing expert
between the alternative suppliers are given below as
a set:
2,1
,
1,4
,
3,4
,
5,3
(22)
The fuzzy decision matrix obtained by evaluation
of alternatives based on determined criteria is
presented as follows (Eq. (23)):
(23)
Then the fuzzy decision matrix is transformed into
the normalization positive triangular fuzzy number
matrix as seen in Eq.(24)
(24)
Then the linear programming model constructed by
combining Eqs. (20), (22) and (24).
Such that
0,8425
0,7667
0,0667
0,5
0,8425
0,7667
0,0667
0,5
0,5286
0,5667
0,0445
0,3889
0,232
0,2
0,0223
0,111
0,217
21
0
0,5467
0,4
0,044
0,222
0,1719
0,3667
0,0222
0,2778
0,172
0,3667
0,022
0,278
0,4678
0,7333
0,0444
0,5556
0,2334
14
0
0,232
0,2
0,0223
0,1111
0,4678
0,7333
0,0444
0,5556
0,4678
0,7333
0,044
0,5556
0,1719
0,3667
0,0222∗40,2778∗4
0,5832
34
0
0,7
0,933
0,0667
0,6667
0,2322
0,2
0,0223
0,1111
0,5467
0,4
0,044
0,2222
0,8425
0,7667
0,0667
0,5
0,6503
53
0
0,7636
1,10
0,0667
0,8333
4,5222
4,933
0,4
3,333
3,8933
4,5333
0,3556
3,1111
4,485
5,2667
0,4
3,6667
0,18310
1
0.011,2,…,
,
,
,
,
,
,
0
1,2,…,
(25)
Solving Eq. (25) using the existing Simplex
method software, we can obtain the optimal
solutions as follows:
,
,
,
0.437,0.200,0.131,0.232
(26)
and
,
,
,
0,0,1.187
,
0,0,1.346
,
0,0,0
,
0,0,0
Using Eq. (21) and combined with Eqs. (26) and
(27), the fuzzy positive ideal solution can be
calculated as:
∗
∗
,
∗
,
∗
,
∗
0,0,2.716
,
0,0,6.73
,
0,0,0
,
0,0,0
And square distance of each alternative from
FPIS can be calculating using Eq. (7) as follows:
2.6916,
2.5431,
2.3756,
2.9303,
2.9707
So the ranking order of five supplier is generated as;
Obviously, the best alternative is
.
4 CONCLUSION
The supplier selection problem has been extensively
studied by the researchers due to being a very
critical activity in Logistics and Supply Chain
Management. In this study, the Fuzzy LINMAP
method is applied to evaluate suppliers in terms of 4
criteria which are cost, delivery, quality and
technical. Supplier selection is a decision making
process which involves uncertainty. The criteria are
defined as the fuzzy numbers and the linguistic
variables to overcome the uncertainty and evaluate
the suppliers in a systematic way. As an illustrative
example, 5 suppliers of a firm in the automotive
SupplierSelectionUsingFuzzyLinearProgrammingTechniqueforMultidimensionalAnalysisofPreference(LINMAP)
125

sector are assessed based on the proposed algorithm.
The main objective of this paper is to bring a
different aspect to the applications of decision
making techniques on supplier selection by using
The Fuzzy LINMAP approach.
LINMAP method generally requires a set of decision
makers’ pairwise preference information between
two alternatives and a decision matrix. If the
number of pairs in the collective set is small, the
optimal criteria weights obtained by the LINMAP
method will be less reliable. If the number of
conflicting preference relations in δ is large, the
LINMAP model may become infeasible. Therefore,
collecting the preference information over the
alternatives is an important issue for the sake of
effectively implementing the LINMAP procedure.
Therefore, future studies may be conduct on this
issue. Another issue on which can be studied is the
value which is subjective and determines the
dominance of consistence over inconsistence in the
model.
What would be the value of h can be
examined with experiments.
REFERENCES
Bereketli, I., Genevois, M.E., Albayrak, Y.E., Ozyol, M.,
2011. WEEE treatment strategies’ evaluation using
fuzzy LINMAP method, Expert Systems with
Applications, 38, 71–79.
Chai, J., Liu, J.N.K., Ngai, E. W. T., 2013. Application of
decision-making techniques in supplier selection: A
systematic review of literature, Expert Systems with
Applications, 40, 3872–3885.
Chen, T.Y., 2013. An interval-valued intuitionistic fuzzy
LINMAP method with inclusion comparison
possibilities and hybrid averaging operations for
multiple criteria group decision making, Knowledge-
Based Systems, 45, 134–146.
Cheng, C.B., 2004. Group opinion aggregation based on a
grading process: a method for constructing triangular
fuzzy numbers, Computers and Mathematics with
Applications, 48, 1619-1632.
Choudhary, D., Shankar, R., 2014. A goal programming
model for joint decision making of inventory lot-size,
supplier selection and carrier selection, Computers &
Industrial Engineering, 71, 1–9.
Guo, X., Zhu, Z., Shi, J., 2014. Integration of semi-fuzzy
SVDD and CC-Rule method for supplier selection,
Expert Systems with Applications 41, 2083–2097.
Junior, F.R.L., Osiro ,L., Carpinetti, L.C.R., 2014. A
comparison between Fuzzy AHP and Fuzzy TOPSIS
methods to supplier selection, Applied Soft Computing
, 21, 194–209.
Junior, F.R.L., Osiro, L., Carpinetti, L.C.R., 2013. A fuzzy
inference and categorization approach for supplier
selection using compensatory and non-compensatory
decision rules, Applied Soft Computing, 13, 4133–
4147.
Kannan, D., Khodaverdi, R., Olfat, L., Jafarian, A., 2013.
A. Diabat, Integrated fuzzy multi criteria decision
making method and multiobjective programming
approach for supplier selection and order allocation in
a green supply chain, Journal of Cleaner Production,
47, 355-367.
Li, D.F., Wan, S.P., 2013. Fuzzy linear programming
approach to multiattribute decision making with
multiple types of attribute values and incomplete
weight information, Applied Soft Computing 13,
4333–4348.
Li, D., Yang, J.B. 2004. Fuzzy linear programming
technique for multiattribute group decision making in
fuzzy environments, Inform. Sci., 158, 263–275.
Srinivasan, V., Shocker, A.D., 1973. Linear programming
techniques for multidimensional analysis of
preference, Psychometrika, 38, 337–342.
Wan, S.P., Li, D.F., 2013. Fuzzy LINMAP approach to
heterogeneous MADM considering comparisons of
alternatives with hesitation degrees, Omega, 41, 925–
940.
Xia, H.C., Li, D.F., Zhou, J.Y., Wang, J.M.,2006. Fuzzy
LINMAP method for multiattribute decision making
under fuzzy environments, Journal of Computer and
System Sciences, 72, 741–759.
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
126
