Combining Development and Evolution

Case Study: One Dimensional Bin-packing

Christopher Rajah and Nelishia Pillay

School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Pietermaritzburg, South Africa

Keywords: Development, Evolution, Biologically-inspired Computing, Bin-packing.

Abstract: The literature highlights the effectiveness of emulating processes from nature to solve complex optimization

problems. Two processes in particular that have been investigated are evolution and development. Evolution

is achieved by genetic algorithms and the developmental approach was introduced to achieve development.

The developmental approach differs from other metaheuristics in that it does not explore the search space

applying intensification and diversification to a complete candidate solution. Instead intensification and

diversification are performed incrementally, at each step in the process of creating a solution. This is based

on an analogy from nature in which a multicellular organism is created incrementally rather than firstly being

completely developed and then improved to be fitter. Evolution on the other hand is used to explore the space

by applying intensification and diversification to randomly created candidate solutions with the aim of

improving the fitness of these candidate solutions and ultimately producing a solution to the problem. Given

that in nature once an organism is initially developed its development or growth does not stop at that point

but certain cells may continue to grow until a certain point in an organism’s life span, it was felt that the

developmental approach terminated prematurely. It was hypothesized that a combination of both these

processes, instantiated with development and followed by evolution, would better emulate the processes in

nature and would be more effective at exploring the search space. The objective of the research presented in

the paper is to test this hypothesis. In terms of search this would mean combining a metaheuristic that applies

intensification and diversification incrementally at each step on partial solutions to create initial candidate

solutions which are then further explored by a metaheuristic that explores the space of complete candidate

solutions. The one-dimensional bin-packing problem was used as a case study to evaluate these ideas. The

hybridization of the developmental approach and genetic algorithm was found to perform better than each of

these approaches applied separately to solve the problem instances. This study was an initial attempt to test

the above hypothesis and has highlighted the potential of this hybridization. Given this future work will apply

this approach to other combinatorial optimization problems.

1 INTRODUCTION

Banzhaf and Pillay (2007) emphasised the need to

take analogies from nature in order to solve complex

optimization problems. The authors highlight two

processes that are essential for this, namely, evolution

and development. Evolution has been emulated to

solve optimization problems by means of

evolutionary algorithms, such as genetic algorithms

(GAs). The developmental approach (DA) was

created to mimic the process of development in

nature. The authors use the domain of examination

timetabling to illustrate the effectiveness of both these

processes in solving complex optimization problems.

Since its inception there have been some revisions

made to the approach to improve its performance

(Pillay and Banzhaf, 2008; Pillay, 2009; Pillay, 2011;

Rajah and Pillay, 2013). The DA has performed

comparatively well to state of the art approaches in

solving the examination timetabling problem, and

was placed amongst the finalists in the examination

timetabling track of the second international

timetabling competition (McCollum et al., 2008). The

developmental approach takes an analogy from the

development of multicellular organisms. Such

organisms are developed incrementally with different

processes contributing to growth at each stage of

development. Whereas other metaheuristics generally

explore the space of candidate solutions by means of

intensification and diversification (Blum and Roli,

2013), the developmental approach performs

intensification and diversification at each stage of

solution construction, i.e. on the space of partial

solutions at each step of creating a solution.

188

Rajah, C. and Pillay, N..

Combining Development and Evolution - Case Study: One Dimensional Bin-packing.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 188-195

ISBN: 978-989-758-157-1

Intensification and diversification are achieved by

emulating the cell biology processes, namely, cell

creation, cell division, cell migration and cell

interaction. Most metaheuristics, like genetic

algorithms, generally explore the space of candidate

solutions that have been already constructed. It is

hypothesized that a hybridization beginning with

development followed by evolution will better

emulate the processes in nature. The reasoning behind

this is that in nature once an initial organism is created

by means of development, development is not

necessarily complete. Certain cells of the organism

will continue to develop until a certain point in the

organism’s life space. In terms of search this means

combining a metaheuristic that incrementally

performs intensification and diversification at each

stage of solution construction with a metaheuristic

that will perform further intensification and

diversification in the space of completed candidate

solutions. The main contribution of this research is to

test this combination. It is anticipated that the

developmental approach will identify potential areas

for optima in the search space which the genetic

algorithm will exploit further. The one-dimensional

bin packing problem (1BPP) was chosen as this is a

well-known combinatorial optimization problem and

is in general one of the domains that are used to

evaluate optimization techniques, e.g. the hyper-

heuristic cross-domain challenge for optimization

(Ochoa et al., 2014). The hybridization of both

approaches was found to work well, producing better

results than the individual application of these

methods to solve problem.

Section 2 gives the background to the study.

Section 3 presents the DA for solving the 1BPP. The

hybrid approach, HDA, is described in section 4. The

methodology used to evaluate the DA, GA and the

HDA applied to the 1BPP is described in Section 5.

Section 6 discusses and compares the performance of

the DA, GA and HDA. Section 7 concludes the study.

2 1BPP

The one dimensional bin-packing problem is an NP-

hard combinatorial optimization problem as it cannot

necessarily be solved in polynomial time. The 1BPP

requires that a minimum number of bins be used to

pack items of different sizes. Each bin has the same

capacity and its capacity may not be exceeded. If a

bin is full then a new bin must be used. This study

focuses on the offline version of the problem in which

the size of the item is known prior to packing (Scholl

et al., 1997).

Fleszar and Hindi (2002) used the perturbation

MBS to create an initial solution which is improved

using variable neighbourhood search. The approach

was successfully applied to the Scholl benchmark set.

In the study conducted by Layeb and Chenche (2012)

initial solutions created by hybridizing the first-fit and

best-first heuristics are optimized using tabu search

(Glover and Luguna, 1997) for the Scholl benchmark

set. In the study conducted by Layeb and Boussalia

(2012) the cuckoo search algorithm, incorporating

principles of quantum computing, is used to solve the

Scholl benchmark problem set. Alvim et al. (2004)

applied a hybrid method to solve the 1BPP. An initial

solution is constructed using the best first decreasing

heuristic. A redistribution strategy is used to improve

bin usability in the solution. A tabu search is then

used to improve the solution. The approach was

applied to both the Scholl and Faulkenauer problem

sets and it produced some of the best results in

literature. Scholl et al. (1997) introduced an approach

called BISON to solve the 1BPP. BISON combines a

variation of MTP with new bound and dominance

rules and reduction procedures, tabu search and a

depth-first search branch and bound method, to solve

this problem. The reduction procedures are similar to

MTP but the approach outperforms MTP when

applied to the Scholl benchmark set.

Lima and Yakawa (2003) used a group based

encoding scheme in a genetic algorithm to solve the

problem. The first fit heuristic is used to create each

individual in the initial population. The method was

able to solve three of the 10 problem instances from

the Scholl problem set considered hard to solve.

Rohlfshagen and Bullinaria (2007) make use of a GA

inspired by exon shuffling in nature. The GA solved

8 of the 10 hard problems in the Scholl benchmark

set. Abidi et al. (2013) also made use of a GA to solve

the 1BPP. Half of the initial population is generated

using the first fit heuristic and the rest is randomly

generated. The approach found optimal solutions to

930 instances from the Scholl benchmark set.

Dokeroglu and Cosar (2014) made use of a parallel

grouping algorithm. The approach to generate the

initial population runs on a processor called the

master node. Thereafter, sub-populations (islands)

are run on separate processors, slave nodes, different

from the master node. Problems in both the Scholl

benchmark problem sets and Faulkenauer benchmark

problem sets were solved using this approach.

A more recent direction of research in this domain

include the use of hyper-heuristics (Lopez-Camacho

et al., 2014) to solve this problem. The authors make

use of a selection construction hyper-heuristic to

construct a solution to the bin-packing problem. The

Combining Development and Evolution - Case Study: One Dimensional Bin-packing

189

low-level heuristics used are the first fit decreasing,

best fit decreasing and a subset of the set of Djang and

Finch heuristics. A genetic algorithm is implemented

to explore the heuristic space. The hyper-heuristic

was successfully used to solve both one dimensional

and two dimensional instances.

3 DEVELOPMENTAL

APPROACH FOR 1BPP

This section describes the DA used for 1BPP. First

the overall algorithm is presented and explained.

Then cell creation, cell division, cell interaction and

cell swap are then described. Algorithm 1 illustrates

the DA used for 1BPP.

Algorithm 1: Developmental Approach for 1BPP.

An organism represents a solution to the 1BPP with

all items allocated to bins. Each cell in the organism

corresponds to a bin and size limit of the cell is

equivalent to the bin capacity for the problem. The

algorithm starts by sorting all the items to be packed

according to the saturation degree. The saturation

degree represents the number of cells, i.e. bins, an

item can be placed in. The saturation degree of the

remaining items is recalculated after the placement of

each item. An item is allocated to the cell with the

least residual space after placement. If the item does

not fit into the existing cell a new cell is created.

There is no restriction on the number of cells

contained in the organism. Both the cell interaction

operator and cell swap operators are called on each

iteration. The algorithm ends when all items have

been packed. Cell and organism representation, cell

division, cell interaction, cell swap and fitness

evaluation are described in the sections below.

3.1 Representation and Cell Creation

As mentioned above the organism developed by the

DA represents the solution to the 1BPP and each cell

in the organism represents a bin in the problem.

Figure 1 illustrates an example of an organism that

has three cells. Cell 1 has three items, namely, items

2, 4 and 7. Cell 2 has four items and cell 3 has two

items. An item cannot be allocated more than once to

a cell or be allocated to more than one cell. One item

is allocated on each iteration. The algorithm begins

by creating a single cell an allocating the first item in

the list to it. If the item cannot be allocated to an

existing cell, cell division is performed. The next

section describes the cell division operator.

3.2 Cell Division

Cell division takes place when an item has to be

allocated and the existing cells have reached the size

limit. A new cell is created and the item is placed in

it. Figure 2 shows an organism that has two cells. Cell

1 has items 1 and 2. Cell 2 has items 3 and 4. Item 5

needs to be added to the organism. The item is too

large to fit in either cell. As a result cell division takes

place. After cell division the organism has three cells.

The new cell is cell 3 with item 5 placed in it. The

next section describes the cell interaction process.

3.3 Cell Interaction

The cell interaction operator attempts to move an item

from a randomly chosen cell to another cell in order

to improve the overall fitness of the organism. The

cell interaction operator is illustrated in Figure 3. The

organism contains three cells, one containing items 2,

4 and 7, the second contains items 5, 6, 9 and 10 and

the third items 1 and 3. Cell 1 is chosen at random.

Item 7, shown in bold with grey shading is chosen at

random from cell 1. Cell 3 is chosen at random and

item 7 is moved to it as the move improves the overall

fitness of the organism.

3.4 Cell Swap

Some cell interactions are reciprocal in nature.

During

an exchange cells may swap items between

themselves. The cell swapping operator first

randomly selects two non-empty cells. A single item

from each cell is chosen at random. An attempt is

made to swap the two items between these two cells.

The move is made if the items fit into the receiving

cells and the fitness of the organism is improved by

the swap. The fitness function is discussed in section

Create_Organism()

Begin

Sort the items to be allocated according to their saturation

degree

Create a single cell

Select the item with lowest saturation degree and place in

the first bin.

Repeat

Resort the remaining items

If there is a feasible cell available

Add the item to the cell with least unused space

Else

Perform cell division and place the item in the new cell

Perform Cell Interaction

Perform Cell Swap

Until all items have been scheduled

End

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

190

3.3.2. The cell swapping operator is illustrated in

Figure 4. Cell 1 and cell 3 are randomly chosen. Item

7 from cell1 and item 3 from cell 3 are randomly

chosen. Item 7 from cell 1 is swapped with item 3

from cell 3 as the move results in a fitter organism.

The swapped items are shown in bold with grey

shading

3.5 Fitness and Evaluation

The fitness of each organism is calculated using the

function in Equation 1 proposed by Faulkenauer

(1996). All cells have the same capacity. The function

favours cells that have less unused space. The

function returns a value between zero and one, where

a higher value is more desirable. A set of completely

full cells, with no cell being partially full, would

return a value of one.

 =

∑

(



/)









where:  = number of cells,





= sum of the

size of all items in cell, and C = cell capacity.

4 HYRBRID APPROACH (HDA)

This section presents the hybrid approach. The hybrid

approach combines the DA discussed in section 3

with a genetic algorithm. As previously mentioned

the DA explores the space of partial solutions at each

step in creating a solution whereas the genetic

algorithm applies intensification and diversification

to the space of complete candidate solutions. It is

anticipated that by combining both these approaches

the developmental approach will identify areas of

potential optima which will be further explored by the

genetic algorithm. Firstly, an overview of the

approach is given, followed by a description of the

GA.

The DA, described in section 3, is used to generate

each individual in the initial population optimized by

the GA. Offspring are created using crossover and

mutation and replace their parents in the population.

Tournament selection is used to choose parents to

create successive generations. Individuals are chosen

at random from the population to form a tournament.

The size of the tournament is a parameter value as it

is problem dependent. The winner of the tournament

is the fittest element which is returned as a parent.

The fitness of the organisms generated by the DA

for the initial population is sufficiently high. This

means that highly fit parents that are selected for

recombination already have cells that are well

packed. The crossover operator needs to preserve this

packing in some cells to some extent to ensure that

the DA efforts are not completely lost in

recombination. The following list outlines the steps

followed by the crossover operator:

1. All cells from both parents are sorted in ascending

order according to the amount of unused space within

each cell.

2. An offspring is created by selecting cells from the

list that are mutually exclusive, i.e. only cells

containing items not yet in the offspring are selected.

If there is more than one cell to choose from then a

cell is selected at random.

3. The remaining items are allocated using the first-

fit heuristic.

4. The DA operators cell interaction and cell swap

are invoked in an attempt to improve the offspring’s

fitness. The application of these operators could be

viewed as local search and hence the genetic

algorithm a memetic algorithm.

The mutation operator is responsible for ensuring

some measure of diversity is maintained in successive

generations. The mutation operator works as follows:

1. Select two cells at random in the offspring.

2. Select two items at random from each cell and

attempt to swap them.

5 METHODOLOGY

The DA, GA and HDA were evaluated on the Scholl

benchmark set for the 1BPP. Table 1 lists the details

of the benchmark set.

Table 1: Scholl Benchmark Set.

Set # Instances Item sizes Bin Capacity # Items

Set1 720 [1-100] {100,120,150

}

{50,100,20

0,500}

Set2 480 [3-9] 1000 {50,100,20

0,500}

Set3 10 [20000-

35000]

100000 200

The benchmark consists of three sets. The first set has

720 instances. Each instance has item sizes in the

range [1,100]. The bin capacities are 100, 120 and

150 and the number of items to be packed is 50, 100,

200 and 500. The second set has 480 instances. The

item sizes are given such that the average number of

Combining Development and Evolution - Case Study: One Dimensional Bin-packing

191

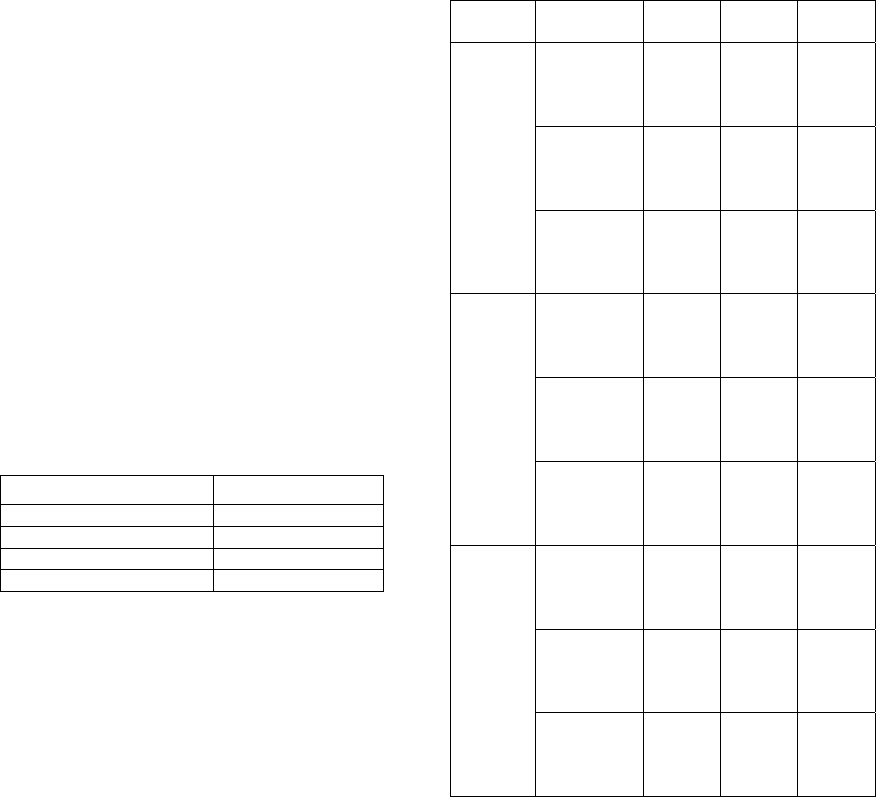
items per bin is in the range [3-9]. The number of

items to be packed is the same as Set1. The third set

has 10 instances. The item sizes are in the range

[20000-35000]. The bin capacity is 100000 and the

number of items is 200. Set 3 is deemed the most

challenging to solve.

The DA, GA and HDA were applied separately to

solve the benchmark problems. The DA, GA and

HDA were applied using three different population

sizes, namely, 100, 300 and 500. This was done to test

the effect of population size on the performance of all

three approaches. Population sizes greater than 500

were not considered. One of the aims of this study is

to test the efficiency of the approaches with smaller

population sizes. In this way computational times can

be kept at acceptable levels. Fifty runs were

performed for each of the population sizes 100, 300

and 500 using a new random number generator seed

for each organism in the population. The tournament

size was fixed at 10. The crossover probability was

set at 0.9 and the mutation probability used was 0.05.

Since the mutation operator attempts to swap items

between two randomly selected bins, it may not

always be successful in that the item intended to be

swapped may not be able to fit into the destination

bin. For this reason the number of attempts for a swap

was set at 100 to avoid the system wasting valuable

computational time unnecessarily. Increasing the

number of attempts beyond this value made little or

no difference to the results achieved. Using a value of

50 was found to be ineffective during testing.

Table 2: GA and HDA parameter values.

Parameter Value

Population sizes 100,300,500

Tournament size 10

Crossover Rate 0.9

Mutation Rate 0.05

To facilitate a comparison in performance of the

GA and HDA, the same parameter values, listed in

Table 2 are used. The fundamental difference

between the GA and HDA is the way the initial

population is generated. In the case of the GA, the

initial population is generated randomly. For the

HDA the DA is used to generate individuals in the

initial population.

The system was implemented in Java using an i5

Core at 2.4 GHz with 4 GB RAM and running

Windows 7 professional. The performance of the DA,

GA and HDA are discussed in the following section.

6 RESULTS AND DISCUSSION

This section reports on the performance of the DA,

GA and HDA described in the previous section in

solving the one-dimensional bin-packing problem.

Section 6.1 examines the performance of the DA, GA

and HDA in solving this problem. Section 6.2

provides a comparison of these methods to other

methods producing the best results for the Scholl

benchmark set.

Table 3: DA, GA and HDA results.

Problem

Set

Population

Size

DA GA HDA

Set1 100 A:634

B:632.5

C:2.278

D: 0.19

A:609

B:599.1

C:33.43

D: 3.39

A:712

B:710.8

C:1.289

D:6.895

300 A:685

B:637.7

C:2.011

D: 0.19

A:681

B:673.3

C:22.9

D: 9.58

A:719

B:713.9

C:0.544

D:22.26

500 A:696

B:642.4

C:1.822

D: 0.22

A:700

B:692.8

C:17.07

D:14.32

A:718

B:716.8

C:0.622

D:34.71

Set2 100 A:434

B:432.5

C:0.944

D: 0.12

A:386

B:379.9

C:37.66

D: 5.6

A:464

B:460.9

C:5.211

D:7.394

300 A:461

B:437.1

C:1.433

D: 0.15

A:433

B:431.4

C:8.267

D:16.83

A:468

B:466.4

C:2.933

D:26.75

500 A:453

B:444.3

C:2.322

D: 0.14

A:465

B:461.8

C:3.288

D: 32

A:480

B:471.3

C:4.9

D:41.31

Set3 100 A: 8

B: 8

C: 0

D: 0.5

A: 0

B: 0

C: 0

D: 0.72

A: 8

B: 8

C: 0

D: 4

300 A: 8

B: 8

C: 0

D: 0.5

A: 4

B: 3.1

C:1.211

D:2.917

A: 9

B: 8

C: 0

D:12.92

500 A: 8

B: 8

C: 0

D: 0.4

A: 5

B: 4.1

C:0.767

D:5.928

A: 9

B: 8

C: 0

D:18.39

6.1 DA, GA and HDA Results

Table 3 lists the results obtained by the DA, GA and

HDA for the three sets of problem instances

comprising the Scholl benchmark set. The table lists

the highest number of instances that were solved to

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

192

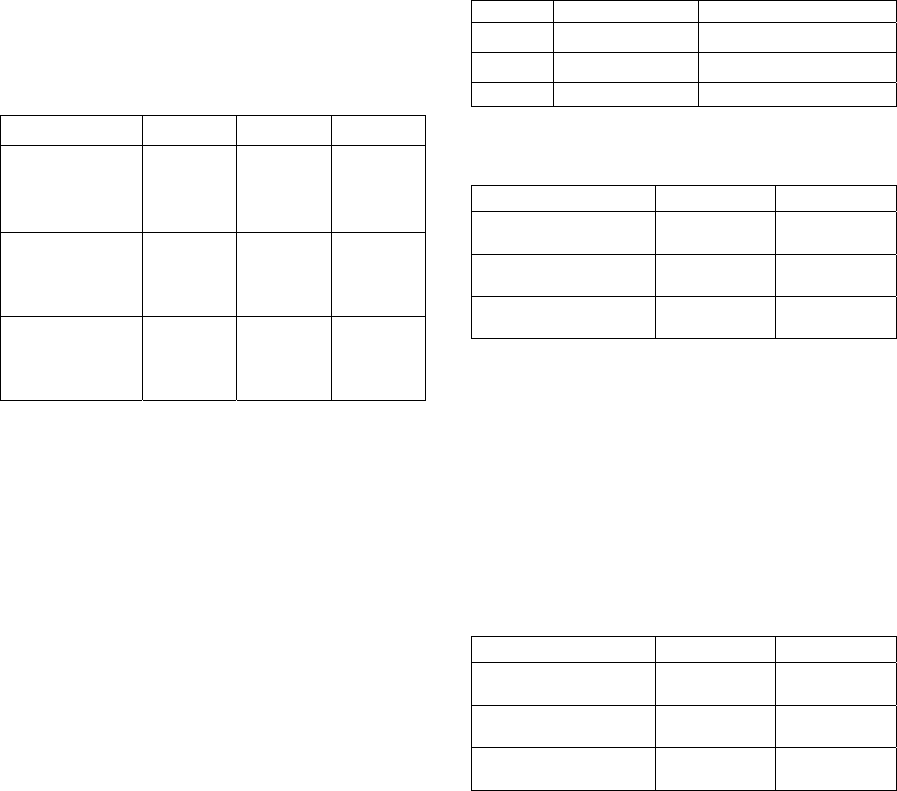
optimality over the 50 runs (A), the average score and

variance score over the 50 runs (B), the average

variance (C) and the average time taken to produce a

solution (D).

Table 4 shows the standard and absolute deviations

for DA, HDA and GA respectively. The absolute

deviation is how far the result is from the optimal

solution and is represented by the number of bins. The

relative deviation is computed as the absolute

deviation divided by the number of bins in the optimal

solution. The table lists the average absolute

deviation (A), maximum absolute deviation (B),

average relative deviation (C) and the maximum

relative deviation (D) over the 50 runs for each set

using the best population size.

Table 4: Absolute and relative deviations for the DA, GA

and HAD.

Problem Set DA GA HDA

Set1 A: 0.035

B: 2

C: 0.03

D: 2.44

A: 0.015

B: 1

C: 0.08

D: 1.55

A: 0.001

B: 1

C: 0.002

D: 1.14

Set2 A: 0.035

B: 2

C: 0.03

D: 2.44

A: 0.065

B: 2

C: 0.09

D: 3.7

A: 0

B: 0

C: 0

D: 0

Set3 A: 0.035

B: 2

C: 0.03

D: 2.44

A: 0.31

B: 2

C: 0.21

D: 1.99

A: 0.01

B: 1

C: 0.18

D: 1.79

From Table 3 it is evident that the DA performs well

as it achieves the optimal solution in more than 97%

of Set1 instances, more than 96% of the Set2

instances and 80% for the Set3 instances. Increasing

the population size seems to have a minimal impact

on the performance of the DA. For Set1 and Set2, the

GA requires a higher population size to produce

better results than the DA. For Set3, it performs

poorly producing much worse results than the DA.

This shows that it does not scale well to more difficult

problems. Increasing the population size for both the

HDA and GA does result in an overall performance

improvement. However, HDA outperforms the GA

using a smaller population of 100 compared to 500

for Set1. For Set2, the HDA using a population of 100

performs similarly to the GA using a population of

500. A similar performance is noted for Set3 when

comparing HDA to GA. The HDA optimally solved

almost all the instances in Set1, all the instances in

Set2 and almost all the instances in Set3. The absolute

and relative deviation also indicates the superior

performance of the HDA over the DA. The non-

optimal solutions derived by the HDA deviated by at

most one from the known optimal. The processing

time for the DA is considerably shorter than HDA and

GA. The GA takes less processing time than the

HDA.

Hypothesis tests were performed to ascertain the

statistical significance of the result that the HDA

performs better than the DA. The levels of

significance, critical values, and decision rules for

these tests are listed in

Table 5. The hypothesis and

Z-values are shown in Table 6.

Table 5: Levels of Significance, critical values and decision

rules.

P Critical Value Decision Rule

0.01 2.33 Reject Ho if Z > 2.33

0.05 1.64 Reject Ho is Z > 1.64

0.1 1.28 Reject Ho if Z > 1.28

Table 6: Hypothesis and Z values for DA and HDA

comparison.

Hypothesis Dataset Z Values

: µ

= µ

HDA

: µ

HDA

> µ

Set1 4.64

: µ

= µ

HDA

: µ

HDA

> µ

Set2 4.40

: µ

= µ

HDA

: µ

HDA

> µ

Set3 0.62

The hypothesis that HDA performs better than DA

was found to be significant at the 1% level of

significance for Set1 and Set2. The hypothesis that

HDA performs better than DA was not found to be

significant at all levels of significance for Set3.

Hypothesis tests were also performed to ascertain

the statistical significance of the result that the HDA

performs better than the GA. The hypothesis and Z-

values are shown in Table 7.

Table 7: Hypothesis and Z values for GA and HDA

comparison.

Hypothesis Dataset Z Values

: µ

HDA

= µ

: µ

HDA

> µ

Set1 37.71

: µ

HDA

= µ

: µ

HDA

> µ

Set2 35.27

: µ

HDA

= µ

: µ

HDA

> µ

Set3 16.07

The hypothesis that HDA performs better than GA

was found to be significant at all levels of significance

for Set1, Set2 and Set3.

Combining Development and Evolution - Case Study: One Dimensional Bin-packing

193

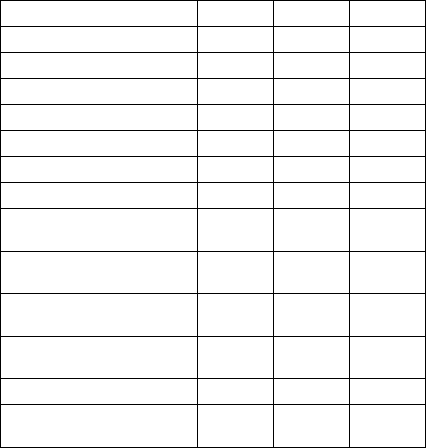
6.2 Comparison to Previous Work

This section empirically compares the performance of

the DA, GA and the HDA to other work solving the

Scholl benchmark problem set in

Table 8. These

methods are discussed in section 2. The table displays

the number of problem instances that are solved to

optimality for each of the problem sets. For example,

696/720 indicates that 696 instances in a set

consisting of 720 instances were optimally solved. In

some cases the method was not applied to all the

problem instances in a chosen set. For example, the

method by Layeb and Boussalia (2012) was applied

to 15 problem instances from Set1, 16 problem

instances from Set2 and all 10 problem instances

from Set3. Therefore, Table 8 shows that their

method solved all 15 problems instances chosen from

Set1, 4 of the 16 problem instances from Set2 and

none of the 10 problem instances from Set3.

Table 8: Number of instances solved for different methods.

Method Set1 Set2 Set3

DA 696/720 453/480 8/10

GA 700/720 465/480 5/10

HDA 718/720 480/480 9/10

Fleszar and Hindi (2002) 694/720 474/480 2/10

Scholl et al. (1997) 697/720 473/480 3/10

Alvim et al. (2004) 720/720 480/480 10/10

Lima and Yakawa (2003) - - 3/10

Layeb and Boussalia

(2012)

15/15 4/16 0/10

Layeb and Chenche

(2012)

5/5 7/15 0/5

Rohlfshagen and

Bullinaria (2007)

- - 8/10

Dokeroglu and Cosar

(2014)

667/720 412/480 8/10

Abidi et al. (2013) 615/720 315/480 0/10

Lopez-Camacho et al.

(2014)

2/2 2/2 -

The comparisons show that the hybrid

improvement heuristic employed by Alvim et al.

(2004) performs the best for all three problem sets. It

is able to solve all problem instances in all three sets

to optimality. The GA inspired by exon shuffling in

nature (Rohlfshagen and Bullinaria, 2007

) was

applied to Set3 and achieved good results. The HDA

has also implemented crossover operators fashioned

to exon shuffling. This may possibly explain the

similarity in performance with all three methods. The

HDA produced better results than the grouping GA

on both Set 1 and Set 2. This may be partly due to the

strong performance of the DA used in the HDA. The

performance of HDA is the closest to the hybrid

method by Alvim et al. in terms of the number of

problem instances solved to optimality in each

dataset. However, the hybrid method has shorter

processing times. This is due to the fact that the

hybrid method optimizes a single candidate solution.

The HDA optimizes a population of individuals at the

same time. Furthermore, the DA has to solve each

problem 100, 200 or 500 times before the GA is

applied. Thus it can be expected that the runtimes are

higher. The performance of the HDA is closely

followed by the DA for all three datasets. The BISON

method, and the perturbation MBS’ with VNS

achieved similar results for all three sets. Whilst the

DA is comparable in performance to other

biologically inspired methods considered here, the

HDA performs the best.

7 CONCLUSION

Previous work has emphasized the importance of both

evolution and development in solving complex

combinatorial optimization problems. As a result of

this the developmental approach was derived to

emulate the process of development in nature. This

study investigates combining development and

evolution and evaluates this hybridization on a new

problem domain, namely, the one-dimensional bin-

packing problem. The standard operators of the DA,

namely, cell division and cell interaction were

implemented. In addition, a third operator taking an

analogy from cell biology, namely, cell swap, was

needed. The DA's performance in solving this

problem was found to be comparative to other

approaches applied to the Scholl benchmark set. The

HDA performs better than the DA and GA in solving

the one-dimensional bin-packing problem and

comparatively, and in a number of cases better, than

other methods that have been applied to the same

benchmark set. The study has highlighted the

potential of the hybridization of both these

approaches and future work evaluate this hybrid

further on additional problem domains including the

travelling salesman and airplane landing problems.

Further theoretical justification for the performance

of the hybrid will also be investigated.

REFERENCES

Banzhaf, W., Pillay, N., 2007. Why Complex Systems

Engineering Needs Biological Development.

Complexity, Vol. 13, No. 2, 12-21.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

194

Pillay, N., Banzhaf, N., 2008. A Developmental Approach

to the Uncapacitated Examination Timetabling

Problem. In Proceedings of PPSN 2008, Lecture Notes

in Computer Science, 276-285.

Pillay, N., 2009. A Revised Developmental Approach to

the Uncapacitated Examination Timetabling Problem.

In Proceedings of SAICSIT 2009, Gauteng,South

Africa, ACM Press,187-192.

Pillay, N., 2011. A Study of Noise Operators in the

Developmental Approach for the Examination

Timetabling Problem. In Proceedings of the 2011 IEEE

Conference on Intelligent Computing and Intelligent

Systems (ICIS 2011), Guangzhou, China, Vol. 3, 534-

538, IEEE Press, November 2011

Rajah, C., Pillay, N. 2013. A Study of introduction of cell

depletion in the Developmental Approach for the

Uncapacitated Examination Timetabling Problem. In

Proceedings of ORSSA 2013, 102-111.

McCollum, B., McMullan, P., Paechter, B., Lewis, R.,

Schaerf, A., DiGapsero, L., Parkes, A. J., Qu, R., Burke,

E.K., 2008. Setting the research agenda in automated

timetabling: The second international timetabling

competition. INFORMS Journal of Computing, Vol.

22, No.1, 120–130.

Ochoa, G., M. Hyde, T. Curtois, , July 2014 J.A. Vazquez-

Rodriguez, J. Walker, M. Gendreau, G. Kendall, B.

McCollum, A. J. Parkes, S. Petrovic andE.K.

Burke."HyFlex: A Benchmark Framework for Cross-

Domain Heuristic Search". In Proceedings of the

European Conference on Evolutionary Computation in

Combinatorial Optimization (EvoCOP 2012), Lecture

Notes in Computer Science, Vol. 7245, pp. 136-147,

2012.

Blum, C., Roli, A. 2013. Metaheuristics in Combinatorial

Optimization: Overview and Conceptual Comparison.

ACM Computing Surveys, vol. 35, no. 3, 268-308.

Scholl, A., Klein, R., Jurgens, C., 1997. Bison: A Fast

Hybrid Procedure for Exactly Solving the One-

Dimensional Bin Packing Problem. Computers and

Operations Research, vol. 24, no. 7, 626-645.

Flezar, K., Hindi, K. S., 2002. New Heuristics for One-

Dimensional Bin-Packing". Computers and Research,

vol. 29, no. 7, 821-839.

Layeb, A., Chenche, S., 2012. A Novel GRASP Algorithm

for Solving the Bin-Packing Problem. International

Journal of Information Engineering and Electronic

Business, vol. 2, 8-14.

Glover, F., Laguna, M. 1997. Tabu Search, Kluwer

Academic Publishers.

Layeb, A., Boussalia, S. R., 2012. A Novell Quantum

Inspired Cuckoo Search Algorithm for Bin-Packing

Problem. International Journal of Information

Technology and Computer Science, vol. 5, pp. 58-67,

2012.

Alvim, A. C., Ribeiro, C. C., Glover, F., Aloise, D. J., 2004.

A Hybrid Improvement Heuristic for the One-

Dimensional Bin Packing Problem. Journal of

heuristics, vol. 10, 205-229.

Lima, H., Yakawa, T., 2003. A New Design Of Genetic

Algorithm For Bin Packing. Evolutionary Computation

, 2003, CEC '03. The 2003 Congress on Evolutionary

Computation, vol. 2, 1044-1049.

Rohlfshagen, P., Bullinara, J. A. 2007. A Genetic

Algorithm With Exon Shuffling Crossover for Hard Bin

Packing Problems. In GECCO '07 Proceedings of the

9th Annual Conference on Genetic and Evolutionary

Computation, New York, USA, 1365-1371.

Abidi, S., Krichen, S., Alba, E., Molina, J. M., 2013.

Improvement Heuristic for Solving the One-

Dimensional Bin-Packing Problem. In Proceedings of

the 5th International Conference on Modeling,

Simulation and Applied Optimization (ICMSAO), 1-5.

Dokeroglu, T., Cosar, A., 2014. Optimization of One-

Dimensional Bin Packing Problem with Island Parallel

Grouping Genetic Algorithms. Computers and

Industrial Engineering, Vol. 75, 176-186.

López-Camacho, E., Terashima-Marin, H., Ross, P.,

Ochoa, G., 2014. A Unified Hyper-Heuristic

Framework for Solving Bin Packing Problems. Expert

Systems with Applications, vol. 41, no. 15, 6876–6889.

Falkenauer, E., 1996. A Hybrid Grouping Genetic

Algorithm For Bin Packing. Journal of Heuristics, vol.

2, 5-30.

Combining Development and Evolution - Case Study: One Dimensional Bin-packing

195