
Enhancing the Accuracy of Mapping to Multidimensional Optimal
Regions using PCA
Elham Bavafaye Haghighi and Mohammad Rahmati
CEIT Department, Amirkabir University of Technology, Tehran, Iran
Keywords: Mapping to Multidimensional Optimal Regions, Multi-classifier, PCA, Code Assignment, Feature
Selection.
Abstract: Mapping to Multidimensional Optimal Regions (M
2
OR) is a special purposed method for multiclass
classification task. It reduces computational complexity in comparison to the other concepts of classifiers. In
order to increase the accuracy of M
2
OR, its code assignment process is enriched using PCA. In addition to
the increment in accuracy, corresponding enhancement eliminates the unwanted variance of the results from
the previous version of M
2
OR. Another advantage is more controllability on the upper bound of V.C.
dimension of M
2
OR which results in a better control on its generalization ability. Additionally, the
computational complexity of the enhanced-optimal code assignment algorithm is reduced in training phase.
By the other side, partitioning the feature space in M
2
OR is an NP hard problem. PCA plays a key role in
the greedy feature selection presented in this paper. Similar to the new code assignment process,
corresponding greedy strategy increases the accuracy of the enhanced M
2
OR.
1 INTRODUCTION
Classification or partitioning a dataset into a
predefined number of classes has a long history
(Zurada, 1992); (Vapnik, 2000); (Theodoridis and
Koutroumbas, 2003). In the set of classification
methods, without considering the trick which is
applied to enhance the accuracy of a classifier, there
are limited basic concepts by which a method
classifies patterns (Zurada, 1992); (Vapnik, 2000);
(Theodoridis and Koutroumbas, 2003); (Bavafaye
Haghighi et al., XXXX); (Bavafaye Haghighi and
Rahmati, XXXX):
(1) Bi-classifier based methods: A bi-classifier is a
decision hyperplane which is able to classify some
given patterns into two groups. By combining the
results of bi-classifiers it is possible to fulfil a multi-
classification task.
(2) Mono-classifier (or centre) based methods: In
Bayes decision theory or clustering methods, each
centre of a class plays the role of a mono-classifier
which determines how much a given pattern belongs
to it (decision confidence).
(3) Dynamical system based: Memories (e.g.
Hopfield) are the examples of dynamical system
based methods. Because of crosstalk noise and the
correlation between attractors, the accuracy of these
methods is not considerable.
The complexity of a classifier is usually more
than/ equal to the number of classes in terms of the
required number of inner products in feature space.
By applying back propagation method (Zurada,
1992); (Vapnik, 2000); (Theodoridis and
Koutroumbas, 2003) or tree (hierarchical) tricks
(Martin et al., 2008); (Ontrup and Ritter, 2006);
)Bavafa et al., 2009); (Ditenbach et al., 2002), it is
possible to reduce computational complexity to a
lower bound related to the number of classes.
However, corresponding decrease could not reach
the bound of one inner product in a multi-
classification task. In addition, in order to raise the
accuracy of classification, more computational
complexity is required in practice. Adding more
neurons to a multilayer layer perceptron (MLP) or
applying k-competition approach in hierarchical
methods are such examples.
In (Bavafaye Haghighi et al., XXXX), a new
concept for multi-classification task is presented
which is called Mapping to Optimal Regions
(MOR). Compared with the concepts of bi-classifier
and mono-classifier, MOR is a Multi-classifier
which is a special purpose method for multi-class
classification. MOR applies only one simple
536
Bavafaye Haghighi E. and Rahmati M..
Enhancing the Accuracy of Mapping to Multidimensional Optimal Regions using PCA.
DOI: 10.5220/0004153305360546
In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 536-546
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

mapping (an inner product) to classify patterns. In
order to define such mapping, a code assignment
process is applied which assigns to each cluster of
patterns a unique code. Corresponding process
enriches the mapping of proposed method by the
topological information of feature space. These
codes play the role of labels with less effect on the
problem called bad labelling. Since there is no need
to assign a code to each disturbed pattern,
corresponding strategy makes the process more
robust to noise.
For a given pattern, mapping is defined
theoretically from feature space to the corresponding
code; however, in practice it maps to a region
around it. Because of the distribution of patterns, it
is impossible to map to the code exactly. As a result,
it is necessary to define optimal regions around each
code in which patterns with a same label/code are
mapped effectively. It is the reason why the new
method is called mapping to optimal regions. The
optimal domain of the regions is estimated using a
multi objective cost function (Sawaragi et al., 1985);
(Bazaraa et al., 2006) to increase the region size and
generalization ability (Kacprzyk, 2007); (Schoelkopf
and Smola, 2002) of the mapping and to reduce the
mapping error. Estimation of optimal domain
concerns the theories of numerical analysis (Stoer
and Bulirsch, 2002); (Heath, 1997) and
regularization (Kacprzyk, 2007); (Schoelkopf and
Smola, 2002).
By taking the advantages of MOR as a multi-
classifier, it is possible to classify a considerable
number of linearly separable classes (e.g. 39 classes)
in high dimensional feature space using only one
inner product (Bavafaye Haghighi et al., XXXX). In
order to obtain better accuracy, Mapping to
Multidimensional Optimal Regions (M
2
OR) and
related theorems are presented (Bavafaye Haghighi
and Rahmati, XXXX). In M
2
OR, an inner product is
partitioned to a number of sub-mappings which are
applied in lower dimensional spaces. As a result, it is
possible to learn more optimal regions using
computational complexity which is approximately
equal to one inner product in feature space.
In this paper, the code assignment process of
M
2
OR is enriched using PCA (Izenman, 2008);
(Jolliffe, 2002). In addition to the increment in
accuracy, corresponding enhancement eliminates the
unwanted variance of the results from the previous
version of M
2
OR. More controllability on the upper
bound of V.C. dimension of M
2
OR is another
advantage of the enhanced version of code
assignment process. It results in a better control on
the generalization ability of M
2
OR. Additionally, it
reduces the computational complexity of the training
phase and guarantees optimal solution for the code
assignment process. More increment in the accuracy
is accomplished by a greedy feature selection using
the most informative orthogonal directions of PCA.
The arrangement of the sections is as follows: In
Sec. 2, a review on MOR family is presented. The
enhanced version of M
2
OR is discussed in Sec. 3.
Some experimental results are prepared in Sec. 4 and
finally, Sec. 5 contains conclusions and future
works.
2 THE FAMILY OF MAPPING TO
OPTIMAL REGIONS
In (Bavafaye Haghighi et al., XXXX); (Bavafaye
Haghighi and Rahmati, XXXX), the concept and the
theoretical aspects of MOR and M
2
OR are
presented. However, Section 2 presents a review
about MOR family and corresponding advantages.
2.1 Challenges of Constructing MOR
In this section, we analyse the error caused by
applying an inner product as a multiclass classifier.
Corresponding mapping is defined by vector ,
given by (1).
〈
,
〉
,
(1)
,
,∈
,
∈,1.
In the above relation x
i
is i
th
training sample, y
i
is
corresponding label and l is the number of training
samples. Superscript .
T
stands for transpose operator.
Using each pattern x
i
as the i
th
row of matrix X and
by defining Y=[y
1
,…, y
l
]
T
, the estimation of a is
given as:
.,
(2)
where .
+
is Moore-Penrose pseudo inverse operator
(Tarantola, 2005; Meyer, 2000). The two main
challenges which f(.) confronts as a multi-classifier,
are summarized as follows. The first one is the result
of bad labelling. Bad labelling occurs when close
patterns do not have close labels. The second
problem is due to the distribution of patterns in
feature space. Such error is related directly to the
radius of cluster sphere.
To reduce the effect of bad labelling in MOR,
closer codes are assigned to the close patterns. For
each cluster of patterns a unique code (called raw
code) is proposed by applying a hierarchical version
of SOM (HSOM) (Kohonen, 1997). The transferred
EnhancingtheAccuracyofMappingtoMultidimensionalOptimalRegionsusingPCA
537

version of these codes to the centre of optimal
regions (optimal codes) play the role of labels with
less effect of bad labelling. The topological
information of patterns is included in the multi-
classifier using optimal codes. For each pattern, the
multi-classifier is defined theoretically from feature
space to the corresponding optimal code. However,
because of the distribution of patterns, it maps to a
region in vicinity in practice. By defining optimal
regions around each code, clusterable patterns with a
same code are mapped in the correct region
effectively. The optimal domain of the regions is
estimated by using a multi objective cost function
with the concern to the theories of numerical
analysis (Stoer and Bulirsch, 2002); (Heath, 1997)
and regularization (Kacprzyk, 2007); (Schoelkopf
and Smola, 2002).
2.2 Raw Codes and Optimal Codes
In order to increase the probability of assigning
appropriate codes, HSOM is applied. In each level
of HSOM, nodes are expanded with a fixed
branching factor (bf). The hierarchy is expanded
until reaching a specific level. Patterns accepted by
sibling sub-clusters, are all accepted by a unique
parent. Therefore, these patterns are topologically
close together. Using (3), closer codes are assigned
to the sibling sub-clusters.
_
_
∗2
_
(3)
In (3),
.
is the ceil operator. The assigned codes to
sub-clusters at the bottom layer of HSOM, are raw
codes. The raw code for the i
th
pattern (c
raw_i
), is the
raw code of sub-cluster which accepts it. Similar to
the vector Y (Sec. 2.1), C
raw
=[c
raw_1,…,
c
raw_l
]
T
is
defined using the raw codes of the training patterns.
Before introducing the multi objective cost
function to estimate optimal domain, the definition
of mapping to optimal codes is required. As a result,
in this section it is assumed that the optimal domain
of the regions (D
o
) is known. D
o
is the distance
between the centre of a region and its border. The
raw codes (c
raw
) which are transferred to the centre
of optimal regions, are called optimal codes (c
o
).
Each optimal code is calculated by multiplying an
odd integer number in D
o
. When optimal codes and
raw codes are arranged in increasing order, the
correspondences between them are determined. The
vector C
o
=[c
o-1
,…, c
o-l
]
T
includes the optimal codes
for training patterns (similar to the vectors of C
raw
and Y). At this step, the mapping from input space to
optimal codes is estimated using (4),
:
→
,
〈
,
〉
;
.
.
(4)
By considering the effect of distribution of patterns,
the optimal code of i
th
pattern is given by:
_
.
1,
2,∈,
.
,
21, ∈.
(5)
2.3 Estimation of Optimal Domain
In order to determine f(.), the optimal value of D
o
is
required. With respect to the theorems of numerical
analysis, increasing the value of D
o
leads to an
extended domain for mapping. Therefore, it seems
that greater values of D
o
are more advantageously
(Stoer and Bulirsch, 2002; Heath, 1997). On the
other hand, smaller values of D
o
have another
benefit, while generalization ability and the error of
the mapping f(x) are proportional to D
o
. The
generalization ability of the mapping f(x) depends on
its derivation with respect to x (i.e.
) (Kacprzyk,
2007). From (4), it is known that:
≅
.
.
⇒
‖
‖
‖
‖
∝
(6)
Therefore, smaller values of
‖
‖
yield less
sensitivity of f(x) to the input variations and it results
in more generalization ability. The dependency
between the error of the mapping (error
o
) and D
o
is
given by:
_
≅
(7)
.
.
.
_
.
.
In (7), error
raw
is the error of the mapping to the raw
codes. For the approximation
≅
.
which
satisfies (6) and (7), it has shown better performance
if both raw and optimal codes have a balance
distribution around zero. As explained earlier on the
importance of the value D
o
, its value is determined
by a multi objective minimization cost function
formulated in (8),
min
1
≅
1
.
.
(8)
Minimizing E causes increasing D
o
as well as
decreasing it, which results in decreasing
‖
‖
indirectly. With respect to the convexity of E in
+
,
it is proved that it has a unique solution in
corresponding domain (Bazaraa et al., 2006);
Sawaragi et al., 1985); (Schoelkopf and Smola,
2002). Since E is a multi-objective cost function, a
weighed summation of the objective terms is
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
538
necessary to emphasize the importance of them.
However, the proper adjustment for such weighs in a
multi objective cost function is a challenging task
(Schoelkopf and Smola, 2002); (Kacprzyk, 2007);
(Sawaragi et al., 1985). As a result, E is
reformulated using other forms of objectives (i.e. E
2
and E
1
in (9) and (10)) (Bavafaye Haghighi et al.,
XXXX).
min
1
.
.
(9)
min
1
.
.
(10)
The solution D
o
in all of the formulations (8), (9)
and (10) correlates inversely with error
. By
determining the nature of D
o
(i.e.1
⁄
), some
finer adjustments is enough to propose the best value
for D
o
. As a result, D
o
is estimated using the general
form presented in (11).
min
⁄
,
. (11)
In (11), is a free parameter adjusted according to
the problem. Experimental results demonstrates that
a set contains 4 members is enough to adjust
corresponding value (Bavafaye Haghighi et al.,
XXXX). The term D
max
is appeared in (11) to avoid
occurrence of infinite value for D
o
.
2.4 The MOR Algorithms
The required steps for training of MOR are as
follows:
1- Assign raw codes by using HSOM.
2- Estimate D
o
by employing (11).
3- Assign optimal codes by using D
o
and C
raw
.
4- Estimate f(.) by applying (4).
5- For each training pattern find corresponding
optimal code by using (5).
6- The label of each optimal region is the major
lable of accepted patterns by corresponding region.
An important note about MOR is that HSOM is
applied to include the topological information of
feature space into the multi-classifier. Therefore,
there is no need to keep its information after
training. In order to apply MOR to find the label of
some test patterns in practice, following steps are
required:
1- For each test pattern find corresponding optimal
code using (5).
2- Retrieve the label of optimal region.
Using the first version of MOR, it is possible to
classify a considerable number of linearly separable
classes (e.g. 39 classes) using only one inner
product. Although MOR reduces complexity in
comparison to the traditional concepts of classifiers,
it is not able to classify data sets with more number
of classes (e.g. 57 classes). The problem stems from
the fact that patterns which are in a hyper cube, are
mapped to the same region. Corresponding
probability increases for more number of classes or
low dimensional datasets.
In order to classify such patterns, a Hierarchical
version of MOR (HMOR) is presented. In Training
process of HMOR, each region that does not pass a
specified threshold of accuracy, is expanded.
2.5 Mapping to Multidimensional
Optimal Regions
Although the complexity of HMOR is lower than
traditional concepts of classifiers, its accuracy for
complex datasets is not acceptable. Unfortunately,
applying a k-competition approach to obtain better
accuracy is not possible. That is the effect of
applying a multi-classifier in contrast to mono-
classifier based approaches in which each mono
classifier has an individual decision confidence
(Zurada, 1992); (Theodoridis and Koutroumbas,
2003); (Martin et al., 2008). However, it is possible
to reduce computational complexity to one inner
product with considerable enhancement in accuracy
using M
2
OR.
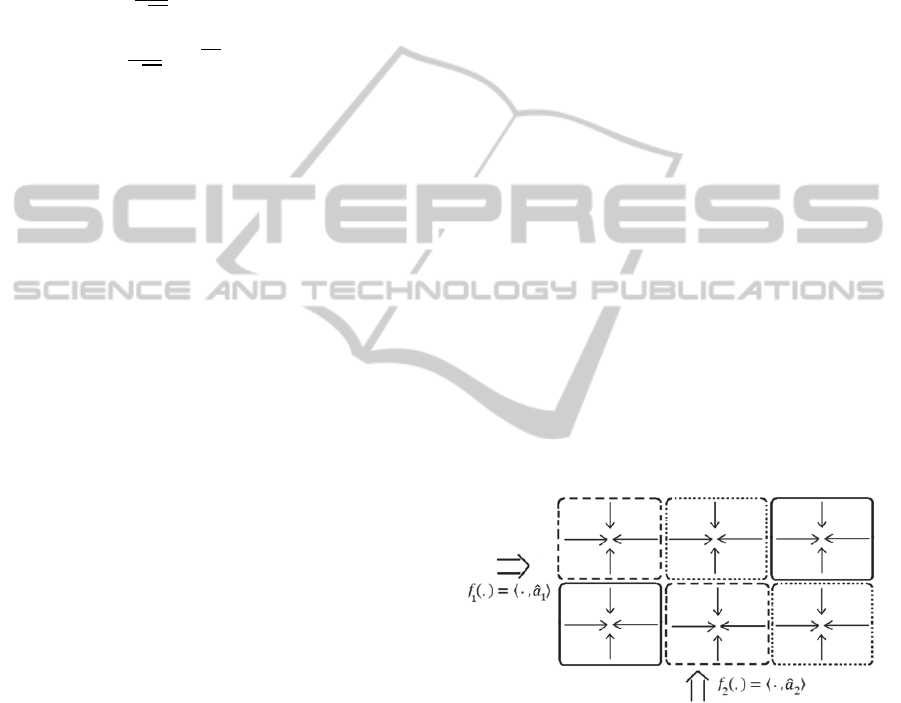
Figure 1: Mapping to multidimensional regions is
illustrated schematically.
For each new expansion in a hierarchical
method, a special subset of variables (or features) is
more effective. Corresponding fact is the main idea
behind M
2
OR which partitions mapping f(.) to a
number of sub-mappings applied in lower
dimensional spaces. Therefore, M
2
OR does not
modify the complexity of the one dimensional
version considerably. However, since the hyper
cubes (defined by the single mapping of MOR) are
partitioned into detailed sub-cubes, accuracy
increases significantly. It is worth reminding that
EnhancingtheAccuracyofMappingtoMultidimensionalOptimalRegionsusingPCA
539

estimating and applying each sub-mapping is
independent from the others. As a result, training
and testing process of M
2
OR can takes the
advantageous of parallel computing (El-Rewini and
Abd-El-Barr, 2005). Figure 1 illustrates mapping to
two dimensional regions schematically. Mapping to
m-dimensional optimal region is defined as f=
(f
1
,…,f
m
) such that
:
⟶,
〈
,
〉
;
(12)
1
,
∈
,
∑
,
,
,…,
,
∈0,1,
1
1,1.
The sequence of
determines which subset of the
variables to be applied for the sub-mapping f
k
(.).
When
1, it means that the j
th
element of x is
selected to be applied by f
k
(.). The condition
∑
1 ensures that the feature space is
partitioned to separated subspaces and also all of the
features are considered for the formation of M
2
OR.
The condition
∑
1 guarantees that the
dimension of each subspace is more than one.
In order to have better accuracy of M
2
OR during
test phase, the probability of mapping to unlabelled
regions should be considered. Since the neighbour
regions accept topologically close patterns, it is
probable that the label of an unlabelled region be
equal to the major label of closest neighbours. K
Nearest Neighbour (KNN) methods require to
compute l number of distances (for l number of
samples) to find the K nearest samples (
Theodoridis
and Koutroumbas, 2003
). However, M
2
OR retrieves
only the label of neighbours by modifying the index
of an unlabelled one. If m
I
(
4) indices are
modified, the label of
neighbours will be
retrieved. It is worth reminding that corresponding
task is an offline process at the end of training phase.
Theoretical and experimental results showed a
considerable enhancement in the accuracy of M
2
OR
in comparison to its hierarchical version. However
more increment in the accuracy is still required to
obtain better results. The sensitivity of the code
assignment process of M
2
OR to the initial weights of
HSOM causes an unwanted variance in its results.
Additionally, in (Bavafaye Haghighi et al., XXXX),
the values of
which are applied to partition the
feature space, is determined with respect to the
natural correlation of the features by the expert. It is
showed in this paper that applying a greedy feature
selection is more advantageously.
3 ENHANCED M
2
OR USING PCA
Principle Component Analysis (PCA) is one of the
oldest and renowned techniques for multivariate
analysis (Izenman, 2008); (Jolliffe, 2002). It is
mainly introduced to reduce the dimensionality of a
dataset in such way that the variation of data be
preserved. It is worth reminding that PCA is not a
classifier in general. For a classification task, a
classifier such as MLP, KNN or etc. is required to be
applied after dimension reduction using PCA.
However, it might be used as a mono classifier
based method when samples with a same label are
almost on a special direction. The limitation of
corresponding assumption does not make PCA an
efficient classifier (VijayaKumar and Negi, 2007).
In this paper, the advantage of detecting the most
informative directions of a dataset using PCA is
applied to increase the accuracy and better
performance of M
2
OR. Both of the code assignment
and feature selection processes are enhanced using
the major orthogonal directions returned by PCA.
After enhancing M
2
OR using PCA during training
phase, there is no need to preserve the information
of principle components. As a result, M
2
OR should
not be considered as an enhanced version of PCA.
3.1 PCA based Code Assignment
It is explained in Sec. 2 that the code assignment
process of M
2
OR is accomplished with respect to the
determined raw codes (Sec. 2.2) and the width of the
optimal regions (Sec. 2.2 & 2.3). In order to estimate
the width of optimal regions (8), one of the objective
terms to increase the generalization ability of the
mapping and to reduce the mapping error depends
on the raw codes. As a result, the process of
determining raw codes plays an important role to
increase the accuracy of M
2
OR.
Using HSOM (Sec. 2.2), the effect of bad
labelling is reduced and the sub-mappings are
enriched with the topological information of
patterns. However, sensitivity of HSOM to the initial
weights of the neurons caused an unwanted variance
in the results of M
2
OR and the bad labelling effect is
still probable. It is demonstrated in this paper that by
applying PCA instead of HSOM the effect of bad
labelling is reduced effectively without imposing
any variance to the accuracy of M
2
OR. In addition,
more control on the generalization ability of the
proposed method, reducing computational
complexity of training phase and optimal solution
are the other advantageous of applying PCA instead
of HSOM.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
540

3.1.1 Enhanced Code Assignment
By projecting samples of a dataset on the major
eigenvector of PCA, the probability of overlapped
projection for different classes is reduced for most of
datasets (Izenman, 2008); (Jolliffe, 2002). Figure 2
demonstrates such situation in
schematically. As
a result, in order to find raw codes for a sub-space
(see Sec. 2.5) using PCA, the major informative
direction of samples (i.e. major eigenvector of
covariance matrix) is more advantageously. By
dividing the projection domain of the major
eigenvector to equal parts, the set of raw codes and
consequently C
raw
are determined (Figure 2).
By applying PCA instead of HSOM, the
computational complexity of training phase of
M
2
OR is reduced. The computational complexity of
code assignment process using HSOM is O(T.l.n.C)
where T is number of training steps and C is the
number of clusters (Kohonen, 1997). In case of
applying PCA, the computational complexity is
O(n
3
+n
2
.l) (Sharma and Paliwal, 2007). Since the
value of T.C is usually more than the dimensionality
of dataset (n), the computational complexity of the
enhanced version of code assignment process is less
than the previous version.
Figure 2: By projecting samples on the major informative
direction of a dataset, the probability of overlapped
projection for different classes is reduced. The set of raw
codes is determined by dividing the projection domain to
equal parts.
3.1.2 Optimality of Solution
Since PCA results in a set of orthonormal basis in
(
Izenman, 2008); (Jolliffe, 2002
)
, the other
mapping directions are the weighted summations of
corresponding basis. By determining the least
overlapped eigenvector of PCA, mapping to each
weighted summation of these bases reduces the
effect of the least overlapped direction. In most
cases, the major eigenvector is the least overlapped
direction. As a result, mapping to the corresponding
direction is the optimal-less overlapped class for
most of datasets.
(a) (b)
Figure 3: There are some exceptional distributions in
which (a) the other eigenvectors are advantageously or (b)
applying a kernel PCA is necessary.
However, there may be some exceptional
distributions in which applying 2
nd
or 3
rd
eigenvector
is advantageously (Figure 3.a) or applying a kernel
PCA is necessary (Figure 3.b). In order to guarantee
the optimality of raw codes in cases similar to Figure
3.a, testing 1
st
, 2
nd
and 3
rd
major eigenvectors is
proposed. For special distributions such as spherical
one (Figure 3.b), with respect to the “No free lunch
theorem” (Schoelkopf and Smola, 2002), meta-
knowledge should be provided to apply the proper
structure of a kernel.
3.1.3 Controllability on V.C. Dimension
By taking the advantage of PCA based code
assignment, the upper bound of V.C. dimension of
M
2
OR and the number of raw codes is more
controllable in comparison to its previous version. In
(Bavafaye Haghighi and Rahmati, XXXX), it is
explained that the upper bound of V.C. dimension of
M
2
OR is equal to
where
is the number of
raw codes and consequently number of optimal
regions for each sub mapping. By applying HSOM,
grows exponentially equal to
where d is the
depth of hierarchy and br is the branching factor.
However, by using PCA based code assignment,
for each sub mapping can be any arbitrary number in
. As a result, the upper bound of V.C. dimension is
more controllable using the proposed enhanced
version of M
2
OR.
3.2 PCA Feature Selection Process
In the first version of M
2
OR, feature partitioning is
accomplished with respect to the natural correlations
in feature space which is determined by a human
expert (Bavafaye Haghighi and Rahmati, XXXX).
EnhancingtheAccuracyofMappingtoMultidimensionalOptimalRegionsusingPCA
541
Corresponding feature partitioning approach is
suggested in (Kumara and Negi, 2008) in order to
solve sub-PCA problem before. An example
illustrates in (Bavafaye Haghighi and Rahmati,
XXXX) in which each two sequence of rows of the
28*28 image of handwritten digits of MNIST
(MNIST) is regarded as the feature of each sub-
mapping.
The problem of feature partitioning is a kind of
graph partitioning which is an NP hard problem.
Instead of partitioning feature space, a greedy
feature selection for each sub-mapping is proposed
in this paper. It increases the accuracy in comparison
to the former method.
3.2.1 Greedy Feature Selection Algorithm
In Sec. 2.5, it is explained that for each new
expansion in a hierarchical method, a special subset
of variables (or features) is more effective. In the
first layers, features which are suitable for a coarse
classification are more important. However, in the
bottom layers, features which contain fine details
play the main role. Finally, a combination of all of
these features is applied for a classification or
clustering task. Such combination is proposed in
M
2
OR by selecting the fine features of the major
principle components.
The importance of variables in each principle
component is different. By sorting the elements of
an eigenvector in increasing order, the effectiveness
of corresponding variables are determined. With
respect to the effect of variable scales on the
covariance matrix and consequently the principle
components, applying PCA on the centered-
normalized version of variables (Izenman, 2008) is
more effective to reduce the effect of variable scales.
Since PCA results in a set of orthonormal basis,
the importance of each variable in an eigenvector is
different from the other eigenvectors. As a result, the
first n/m variables of k
th
major eigenvector, is
considered for f
k
(.). With respect to the different
degree of importance of the selected variables in the
other eigenvectors, it is probable that corresponding
set of features is not selected for the other sub-
mappings. However, in order to guarantee that all of
the features are applied in the classification process,
after feature selection process for the first m-1 sub-
mappings, the residual-non selected variables are
assigned to the last sub-mapping (i.e. f
m
(.)).
According to the explanations about feature
selection process, corresponding algorithm is
summarized as follows:
1- Apply PCA on the centered-normalized dataset.
2- Select the first m-1 major eigenvectors.
3- For 11: Select the first n/m fine
variables of k
th
eigenvector for f
k
(.) and set
11 for the selected variables accordingly.
4- Select the residual features for f
m
(.) and set
1 1 for corresponding variables
accordingly.
By considering the probability of selecting a variable
more than one time in feature selection process, the
condition
∑
1 of (12) should be rewritten as
∑
1. Experimental results confirm that the
probability of selecting a variable more than one
time is infrequent. The number of repeated features
is less than the half of total number of variables in
almost all cases. Applying fine variables of
informative orthonormal directions increases the
accuracy of M
2
OR considerably.
3.3 Enhanced M
2
OR Algorithms
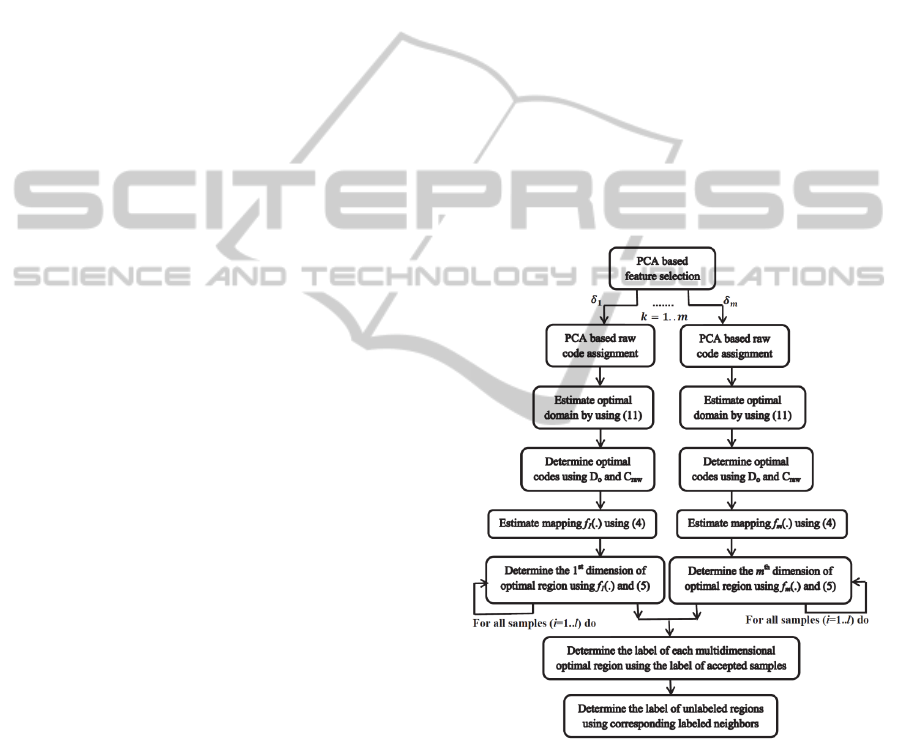
Figure 4: The Algorithm of training enhanced M
2
OR.
Estimating the sub-mappings can take the advantage of
parallel computing.
According to the enhancements in code 1 process
and feature selection, the enhanced training process
of M
2
OR is summarized in Figure 4. After
determining the multidimensional optimal region of
each training sample, corresponding region is
labeled with respect to the major lable which is
accepted by it. For unlabeled regions which have
labeld neighbours, their label is detemined with
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
542

respect to the most frequent labels of the neighbours.
By determining sub-mappings after training, they are
applied in the test phase as illustrated in Figure 5.
Figure 5: The Algorithm of testing enhanced M
2
OR.
Applying sub-mappings can take the advantage of parallel
computing.
4 EXPERIMENTAL RESULTS
In (Bavafaye Haghighi et al., XXXX), the concept of
Mapping to Optimal Regions as a multi-classifier is
presented by which a considerable number of
linearly separable classes are classified by applying
only one inner product in feature space. Mapping to
Multidimensional Optimal Regions and related
theorems about solution existence and potential
abilities of learning in terms of V.C. dimension and
growth function are presented in (Bavafaye
Haghighi and Rahmati, XXXX). The focus of
experimental result in this paper is presenting
considerable enhancement in the accuracy of M
2
OR
by applying the least expected computational
complexity.
4.1 Experiments Setup
Table 1 presents the specification of datasets which
are applied in this paper. MNIST (MNIST) is the set
of handwritten digits. Each digit has been size-
normalized and cantered in a fixed size (28*28)
image. COIL100 (Nene et al., 1996) contains colour
images of 100 different objects which are turned by
5
°
. As a result, there are 72 images from different
views for each object. In COIL-A, 18 images from
each object (which are turned 20
°
) are applied to
train and the 54 remaining images are used to test. In
COIL-B, 36 images (by turning each object 10
°
) are
applied to train and the remaining 36 images are
used to test.
Similar to (Kietzmann et al., 2008), from each
image of COIL100, 292 dimensional features are
extracted. Each extracted feature contains 64*3
dimension for the histograms of Lab channels, 64
dimensional histogram of Discrete Cosine
Transformation (DCT), 8 dimension for Hu
moments in addition to the logarithm form of their
absolute values, 10 dimensional shape information
which contains centroid, compactness, perimeter,
eccentricity, circularity, aspect ratio, elongation,
maximum and minimum diameters in addition to the
logarithm of their absolute values.
Table 1: Specifications of the applied datasets.
n C l-train l-test
MNIST
784 10 60000 10000
Forest
54 7 290321 290321
COIL-A
292 100 1800 5400
COIL-B
292 100 3600 3600
Robot
24 4 4911 546
Segment
19 7 210 2100
MFeat
649 10 1800 200
* The abbreviations are given in the text.
Other datasets which are Forest Cover Type
(Forest), Wall Following Robot (Robot),
Segmentation (Segment) and Multiple Feature Digit
(MFeat), are downloaded from UCI repository (UCI
repository). No feature extraction is applied on the
UCI datasets and also on MNIST digits.
Table 2 presents the parameter settings for the
enhanced M
2
OR for different datasets. In most
cases, applying the 1
st
principle component
optimizes the set of raw codes in 66% of datasets.
Table 2: The parameters of the enhanced M
2
OR.
m
N
c
Principle
Component No.
MNIST
16 4 1
s
t
Forest
12 8 1
s
t
COIL-A
8 14 1
s
t
COIL-B
8 14 1
s
t
Robot
9 12 1
s
t
Segment
8 9 2
nd
MFeat
8 10 2
nd
4.2 Increasing the Accuracy of Results
Table 3 presents the error rate and the computational
complexity (CC) of (1) M
2
OR with HSOM based
code assignment and sequential feature partitioning
(M
2
OR+HSOM+SP), (2) enhanced M
2
OR with PCA
based code assignment and sequential partitioning
(M
2
OR+ PCA+SP), (3) enhanced M
2
OR with PCA
based code assignment and the proposed feature
selection process (M
2
OR+PCA+FS) and (4) other
classifiers (Yang et al., 2002); (Fu et al., 2010);
(Bala and Agrawal, 2009); (Sen and Erdogan, 2011);
(Villegas and Paredes, 2011); (LeCun, et al., 1986;
MNIST). Since HSOM is sensitive to the initial
weights of neurons, its least, mean and variance of
error rates are reported. According to the
EnhancingtheAccuracyofMappingtoMultidimensionalOptimalRegionsusingPCA
543

enhancements of M
2
OR, the error rate of
corresponding method is reduced considerably in
comparison to its previous versions. It eliminates the
unwanted variance of the results.
According to Table 3, the error rates of enhanced
M
2
OR for Forest and Robot datasets are comparable
with the state of the art methods (Fu et al., 2010);
(Sen and Erdogan, 2011). The accuracy of
classification for COIL100 and Segment is not better
than Support Vector Machine (SVM) approaches
(Yang et al., 2002); (Bala and Agrawal, 2009);
however, enhanced M
2
OR has an acceptable
difference with corresponding methods. It seems that
the distribution of patterns in MNIST and MFeat are
not proper to be applied by the current version of
M
2
OR (with inner product kernel) (LeCun, et al.,
1986); (MNIST); (Villegas and Paredes, 2011).
Applying M
2
OR in Reproducing Kernel Hilbert
Space (RKHS) (Hofmann et al., 2008); (Schoelkopf
and Smola, 2002); (Ben-Hur et al., 2001) can be
more advantageously which is recommended in Sec.
5.
4.3 Computational Complexity
The main advantage of the M
2
OR as a multi-
classifier is reducing computational complexity
which is outstanding in comparison to the other
concepts of classifiers. By considering total number
of inner products in
as Computational
Complexity (CC), corresponding value for M
2
OR is
given as follows (Bavafaye Haghighi and Rahmati,
XXXX):
∑
/.
(13)
In (13),
∑
is total number of multiplies of
sub-mappings and m is the number of divisions to
find the index of optimal code. It is assumed here
that the cost of division and multiply is the same. r is
the cost of retrieving the label of optimal region.
Retrieving each label requires m-1 number of
multiplies which is a compiler task. As a result, r is
not more than m-1. It is worth reminding that by
applying the advantage of parallel computing (El-
Rewini and Abd-El-Barr, 2005), CC is reduced in
comparison to (13).
The values of CC for other methods are
presented with respect to the number of hidden
neurons, support vectors or the given complexities.
If the exact number of support vectors is not given in
a paper, the minimum and maximum number of
support vectors for each hyperplane are considered
as n/2 and n respectively. As a result, upper and
lower bounds of CC are given in Table 3 for two
datasets. In (MNIST), a complete list of the error
rates of the previous and state of the art methods is
presented. By applying a Multi-Layer Perceptron
(MLP) with 1000 hidden neurons (CC>1000), the
error rate is approximately equal to 4. Although CC
of enhanced M
2
OR (i.e. CC=1.6) is considerably
less than MLP, the importance of more increasing
the accuracy of M
2
OR is not diminished for
corresponding dataset.
5 CONCLUSION AND FUTURE
WORKS
Since Mapping to Multidimensional Optimal
Regions (M
2
OR) is a special purposed method for
multi-classification task, it reduces computational
complexity considerably in comparison to the other
concepts. By enriching the code assignment process
using the major informative directions of samples
(i.e. principle components), the probability of
overlapped mapping for different classes decreases
and the accuracy of M
2
OR increases. Additionally,
the unwanted variance of the results which is the
result of the sensitivity of Hierarchical Self Organi-
Table 3: The error rate and the CC of enhanced M
2
OR in comparison to the previous versions and other methods.
M
2
OR+HSOM+SP M
2
OR+PCA+SP M
2
OR+PCA+FS Other methods
L. Err. M. Err. CC Err. CC Err. CC Err. CC Method
MNIST
22.3 27.5±5.3 1.03 20.7 1.03 18.04
1.6 4.5 >
1000 < MLP
Forest
34.48
35.7±1.3
1.42
30.05
1.42
22.5
2.16
22.66 113< <227 MLSVM
23.81 5028.6 LSVM
COIL-A
19 23.2±5.1 1.05 16.6 1.05 14.6
1.49 8.7
5050 < LSVM
COIL-B
16.5 19.5±2.7 1.05 13.38 1.05 10.13
1.49 3.96
5050 < LSVM
Robot
4.4
4.8±1.9
1.7
4.21
1.7
3.9
2.5
2.5
38480
Combination
of Classifiers
Segment
19.8 27.3±5.1 1.78 25.81 1.78 19.76
2.7 10.48
149< <843 NLSVM
MFeat
30.1 36.5±5.4 1.02 29.75 1.02 18.5
1.29 0.8
66 LDPP
CC: Computational Complexity; SP: Sequential Partitioning; FS: Feature Selection using PCA; Err.: Error; L. Err.: Least Error;
M. Err.: Mean Error. MLP: Multi-Layer Perceptron; (N)LSVM: (Non) Linear Support Vector Machine; MLSVM: Mixing LSVMs;
LDPP: Learning Discriminant Projections and Prototypes.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
544

zing Map (HSOM) to the initial weights of its
neurons, is removed. Increasing the controllability
on the upper bound of Vapnik-Chervonenkis (V.C.)
dimension and lower complexity during training
phase in comparison to HSOM are other advantages
of applying PCA based code assignment. Since
principle components are orthogonal set of basis,
testing the first major components guarantees
optimizing the set of raw codes for each sub-
mapping.
In addition, applying the fine variables of the
major principle components, increase the accuracy
of the results in comparison to sequential feature
partitioning approach. The orthogonality of the
components reduces the probability of selecting a
variable more than one time. It is demonstrated that
the accuracy of enhanced M
2
OR is comparable with
the state of the art methods for Forest Cover Type
and Wall Following Robot datasets with
incomparable lower computational complexity;
however, it requires more enhancements in the line
of accuracy for other datasets. Therefore, we
propose to apply enhanced M
2
OR in Reproducing
Kernel Hilbert Space (RKHS) for future works.
Online learning is another important aspect to
improve the abilities of M
2
OR.
ACKNOWLEDGEMENTS
This paper is supported in part by Information and
Communication Technology (ICT) under grant T-
19259-500 and by National Elites of Foundation of
Iran.
REFERENCES
Bala, M., Agrawal, R. K., 2009, Evaluation of Decision
Tree SVM Framework Using Different Statistical
Measures, International Conference on Advances in
Recent Technologies in Communication and
Computing, 341-345.
Bavafa, E., Yazdanpanah, M. J., Kalaghchi, B., Soltanian-
Zadeh, H., 2009, Multiscale Cancer Modeling: in the
Line of Fast Simulation and Chemotherapy,
Mathematical and Computer Modelling 49,
1449_1464.
Bavafaye Haghighi, E., Rahmati, M., Shiry Gh., S.,
XXXX, Mapping to Optimal Regions; a New Concept
for Multiclassification Task to Reduce Complexity, is
submitted to the journal of Experimental &
Theoretical Artificial Intelligence.
Bavafaye Haghighi, E., Rahmati, M., XXXX, Theoretical
Aspects of Mapping to Multidimensional Optimal
Regions as a Multiclassifier, is submitted to the
journal of Intelligent Data Analysis.
Bazaraa, M., Sherali, H. D., Shetty, C. M., 2006,
Nonlinear Programming, theory and Algorithms, 3
rd
ed., John Wiley and Sons.
Ben-Hur, A., Horn, D., Ziegelmann, H. T., Vapnik, V.,
2001, Support Vector Clustering, Journal of Machine
Learning Research 2, 125-137.
Ditenbach, M., Rauber A., Merkel, D., 2002, Uncovering
hierarchical structure in data using the growing
hierarchical self-organizing map, Neurocomputing 48,
199-216.
El-Rewini, H., Abd-El-Barr, M., 2005, Advanced
Computer Architechture and Parallel Processing,
John Willey and Sons.
Fu, Zh., Robles-Kelly, A., Zhou, J., 2010, Mixing Linear
SVMs for Nonlinear Classification, IEEE
Transactions On Neural Networks 21, 1963-1975.
Heath, M. T., 1997, Scientific Computing: An Introductory
Survey, Mc Graw Hill.
Hofmann, T., Scheolkopf, B., Smola, A. J., 2008, Kernel
Methods in Machine Learning, The Annals of
Statistics 36, 1171–1220.
Izenman, A. J., 2008, Modern Multivariate Statistical
Technics, Springer.
Jolliffe, I. T., 2002, Principle Component Analysis, 2
nd
ed.,
Springer.
Kacprzyk, J., 2007, Challenges for Computational
Intelligence, in: A Trend on Regularization and Model
Selection in Statistical Learning: A Bayesian Ying
Yang Learning Perspective, Springer, 343-406.
Kietzmann, T. C., Lange, S., M., Riedmiller, 2008,
Increamental GRLVQ: Learning Relevant Features for
3D Object Recognition, Neurocomputing 71, 2868-
2879.
Kohonen, T., 1997, Self Organizing Maps, Springer Series
in Information Science, 2
nd
ed., Springer.
Kumara, K. V., Negi, A., 2008, SubXPCA and a
generalized feature partitioning approach to principal
component analysis, Pattern Recognition, 1398-1409.
LeCun, Y., Bottou, L., Bengio Y., Haffner, P., 1986,
Gradient-Based Learning Applied to Document
Recognition, Proceedings of IEEE, 86, 2278-2324.
Martin, C., Diaz, N. N., Ontrup, J., Nattkemper, T. W.,
2008, Hyperbolic SOM-based Clustering of DNA
Fragment Features for Taxonomic Visualization and
Classification, Bioinformatics 24, 1568–1574.
Meyer, C. D., 2000, Matrix Analysis and Applied Linear
Algebra, SIAM.
MNIST: http://yann.lecun.com/exdb/mnist/.
Nene, S. A., Nayar, Sh. K., Murase, H., 1996, Columbia
Object Image Library (COIL 100), Technical Report
No. CUCS-006-96, Department of Computer Science,
Columbia University.
Ontrup, J., Ritter, H., 2006, Large-Scale data exploration
with the hierarchically growing hyperbolic SOM,
Neural Networks 19, 751-761.
Sawaragi, Y., Nakayama, H., Tanino, T., 1985, Theory of
Multiobjective Optimization, Academic Press.
Schoelkopf, B., Smola, A. J., 2002, Learning with
EnhancingtheAccuracyofMappingtoMultidimensionalOptimalRegionsusingPCA
545

Kernels, MIT press.
Sen, M. U., Erdogan, H., 2011, Max-Margin Stacking and
Sparse Regularization for Linear Classifier
Combination and Selection, Cornell University
Library, arXiv:1106.1684v1 [cs.LG].
Sharma, A., Paliwal, K. K., 2007, Fast principal
component analysis using fixed-point algorithm,
Pattern Rcognition Letters, 1151-1155.
Stoer, J., Bulirsch, R., 2002, Introduction to numerical
analysis, Springer.
Tarantola, A., 2005, Inverse Problem Theory and Methods
for Model Parameter Estimation, SIAM.
Theodoridis, S., Koutroumbas, K., 2003, Pattern
Recognition, 2
nd
ed., Elsevier Academic Press.
UCI Repository: http://archive.ics.uci.edu/ml/.
Vapnik, V. N., 2000, The Nature of Statistical Learning
Theory, 2
nd
ed., Springer.
Vijaya Kumar, K., Negi, A., 2007, A Feature Partitioning
Approach to Subspace Classification, IEEE TENCON
2007, 1-4.
Villegas, M., Paredes, R., 2011, Dimensionality reduction
by minimizing nearest-neighbor classification error,
Pattern Recognition Letters 32, 633-639.
Yang, M. H., Roth, D., Ahuja, N., 2002, Learning to
Recognize 3D Objects with SNoW, Neural
Computation 14, 1071-1104.
Zurada, J., 1992, Introduction to Artificial Neural Systems,
West Publishing Company.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
546
