Predicting Fault-proneness of Object-Oriented System Developed

with Agile Process using Learned Bayesian Network

Lianfa Li

1,2

and Hareton Leung

LREIS, Inst. of Geog. Sciences and Resources Research, CAS, Beijing, China

Department of Computing, The Hong Kong Polytechnic University, Kowloon, Hong Kong

Keywords: Object-Oriented Systems, Fault-proneness, Software Quality, Data Mining.

Abstract: In the prediction of fault-proneness in object-oriented (OO) systems, it is essential to have a good prediction

method and a set of informative predictive factors. Although logistic regression (LR) and naïve Bayes (NB)

have been used successfully for prediction of fault-proneness, they have some shortcomings. In this paper,

we proposed the Bayesian network (BN) with data mining techniques as a predictive model. Based on the

Chidamber and Kemerer’s (C-K) metric suite and the cyclomatic complexity metrics, we examine the

difference in the performance of LR, NB and BN models for the fault-proneness prediction at the class level

in continual releases (five versions) of Rhino, an open-source implementation of JavaScript written in Java.

From the viewpoint of modern software development, Rhino uses a highly iterative or agile development

methodology. Our study demonstrates that the proposed BN can achieve a better prediction than LR and NB

for the agile software.

1 INTRODUCTION

In the prediction of fault-proneness (the probability a

software component contains at least one fault) as a

critical indicator of software quality in object-

oriented systems, it is essential to have informative

predictive factors (D'Ambros et al., 2012) and a

good prediction model. There are many choices for

predictive factors, including product metrics,

processing and external metrics, and other

combinations of factors (Pai and Dugan, 2007).

There are also many choices for the prediction

model which is as important as the predictive factors

in determining the accuracy of the fault-proneness

prediction (Menzies et al., 2007).

Logistic regression has been extendedly used for

the fault-proneness prediction as a benchmark

method. Recently other learners such as decision

tree (Singh et al., 2009), random forest (Guo et al.,

2004), naive Bayes (NB) (Menzies et al., 2007),

neural network (Singh et al., 2008) and support

vector machine (Singh et al., 2009) have been

successfully used to predict fault-proneness.

These prediction methods have some

shortcomings. For example, logistic regression

(Hosmer and Lemeshow, 2000) assumes a linear and

addictive relationship between predictors and the

dependent variable (fault-proneness) on a logistic

scale. This assumption is simplistic and presents a

critical constraint on the model (Gokhale and Lyn,

1997). Further, the form of logistic regression also

makes it difficult to combine qualitative predictors

such as processing or external factors with numeric

product metrics. NB has the constraints of assuming

the conditional independence of predictors and the

normal distribution of continuous product metrics as

predictors (John and Langley, 1995). Recently, Pai

and Dugan (Pai and Dugan, 2007) used LR to

construct and parameterize their BN model which

did not avoid the typical constraints associated with

LR. Other approaches such as random forest and

neural network were black-box models and less

interpretable although having a good prediction

performance.

In this paper, we present a Bayesian network as a

learning model. In this model, we examine the

performance of BN against the LR and NB using the

continual versions of the open-source JavaScript tool,

Rhino which has been developed using the agile

software development processes. Our study shows

that the learned BN was mostly better than the LR

and NB from the cross-validation test and from the

validation of the continual Rhino versions. The

results suggest that our proposed BN is valuable as a

Li L. and Leung H..

Predicting Fault-proneness of Object-Oriented System Developed with Agile Process using Learned Bayesian Network .

DOI: 10.5220/0004392900050016

In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 5-16

ISBN: 978-989-8565-60-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

prediction model of fault-proneness.

The agile software development strategy is an

iterative and incremental approach to software

development which is performed in a highly

collaborative manner that is cost effective and meets

the changing needs of its stakeholders (Ambler and

R., 2002; Cohn, 2006; Herbsleb, 2001). Agile

Alliance defined 12 principles for the agile

development process (Cohn, 2006 ). Olague et al.

argued that Rhino was a typical software product

using the agile development strategy (Olague et al.,

2007). Also, their study showed that product metrics

(e.g. C-K metrics) at the class level were useful for

the fault-proneness prediction of the agile OO

systems. Therefore, our case study uses the C-K

metrics and the cyclomatic complexity metrics to

examine the difference in performance of the

prediction methods (LR, NB and our proposed BN)

for fault-proneness.

This paper makes the following contributions. First,

we present the BN with data mining techniques for

learning and optimization and demonstrate its

distinguishing features and advantages (more

flexible network topology for including quantitative

and qualitative predictors, and wide choices of

optimal learning algorithms) in comparison to the

LR and NB models. Second, based on the cross-

validation and the validation of the continual

versions of Rhino, we show the superior

performance of the learned BN. Third, our study

adds to the body of empirical knowledge about the

prediction models of fault-proneness.

The rest of this paper is organized as follows. In

section 2, we introduce the metrics used, the system

under study and the collection of predictors. In

section 3, we describe the modelling techniques of

LR, NB and BN and compare them. Section 4

presents data analysis procedures and methods

employed. The experimental results are reported and

discussed in section 5. In section 6, we draw

conclusions and suggest some future work.

2 BACKGROUND

2.1 Metrics used

We use the Chidamber and Kemerer’s (C-K) metric

suite and the cyclomatic complexity metrics at the

class level as predictors. The C-K metric suite has

been empirically validated to be useful for the fault-

proneness prediction in many studies (Basili et al.,

1996; Briand et al., 2000; Olague et al., 2007) and so

are the cyclomatic complexity metrics (Cardoso,

2006). It is assumed that the higher the metric value,

the more fault-prone is the class.

In the C-K metrics implemented for our research

(Chidamber and Kemerer, 1994), LCOM represents

a later variation of the original LCOM that has been

shown to have a better predictability (Harrison et al.,

1998). These metrics are listed below:

 WMC (Weighted Methods per Class): The

number of methods implemented in a class.

 DIT (Depth of Inheritance Tree): Maximum

number of edges between a given class and a

root class in an inheritance graph (0 for a

class which has no base class).

 NOC (Num. Children): A count of the

number of direct children of a given class.

 CBO (Coupling Between Objects): Counts

other classes whose attributes or methods are

used by the given class plus those that use the

attributes or methods of the given class.

 RFC (Response For a Class): A count of all

local methods of a class plus all methods of

other classes directly called by any of the

methods of the class.

 LCOM (Lack of Cohesion of Methods):

Number of disjoint sets of local methods, no

two sets intersect, and any two methods on

the same set share at least one local variable

(1998 definition).

The cyclomatic complexity can be extracted from

each of the methods (McCabe, 1976).

 CCMIN: Minimum of all cyclomatic

complexity values of the methods for a class.

 CCMAX: Maximum of all cyclomatic

complexity values of the methods for a class.

 CCMEAN: Arithmetic average of all

cyclomatic complexity values of the methods

for a class.

 CCSUM: Sum of all cyclomatic complexity

values of the methods for a class.

2.2 System under Study

Mozilla’s Rhino (Boyd, 2007) was used in our study.

Rhino is an open-source implementation of

JavaScript completely written in Java. This system

has been developed by three programmers, all in

separate locations worldwide, following an iterative

cycle from 2 to 16 months. The core components

and their related bug data of versions 1.5R3, 1.5R4,

1.5R5, 1.6R1, and 1.6R2 of Rhino were analyzed in

our study. Fault reports of Rhino exist in the online

Bugzilla repository (Bugzilla, 2005). We examined

the change logs of each version of Rhino which

listed the post-release bugs that were resolved for

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

the next version. Bug fixes were cross-referenced

with classes affected by each bug/fix.

2.3 Collection of Metrics

In our study, we mainly used the open-source Java

metric toolkits for extracting the product metrics

from Rhino. Spinellis’s CKJM (Spinellis, 2006) has

been integrated in our program to collect the C-K

metrics, and CYVIS, a software complexity

visualiser (CYVIS, 2007) has been adapted to

extract the cyclomatic complexity metrics (CCMAX,

CCMEAN, CCSUM and CCMIN) at the class level

from the Java class files.

Table 1: Descriptive Statistics of Predictive Factors Used.

Note that our initial analysis shows that, among the

complexity metrics, CCMIN has little contribution

to the fault-proneness prediction and hence it is

removed from the set of predictors. Also, there is a

large correlation between CCMAX, CCMEAN and

CCSUM. This leads to the problem of

multicollinearity (Olague et al., 2007). After

comparing their correlation with the C-K metrics,

we select the complexity metric with a good

predictability and less redundancy of information.

Consequently, CCMAX is chosen in our case study,

as shown in Table 1.

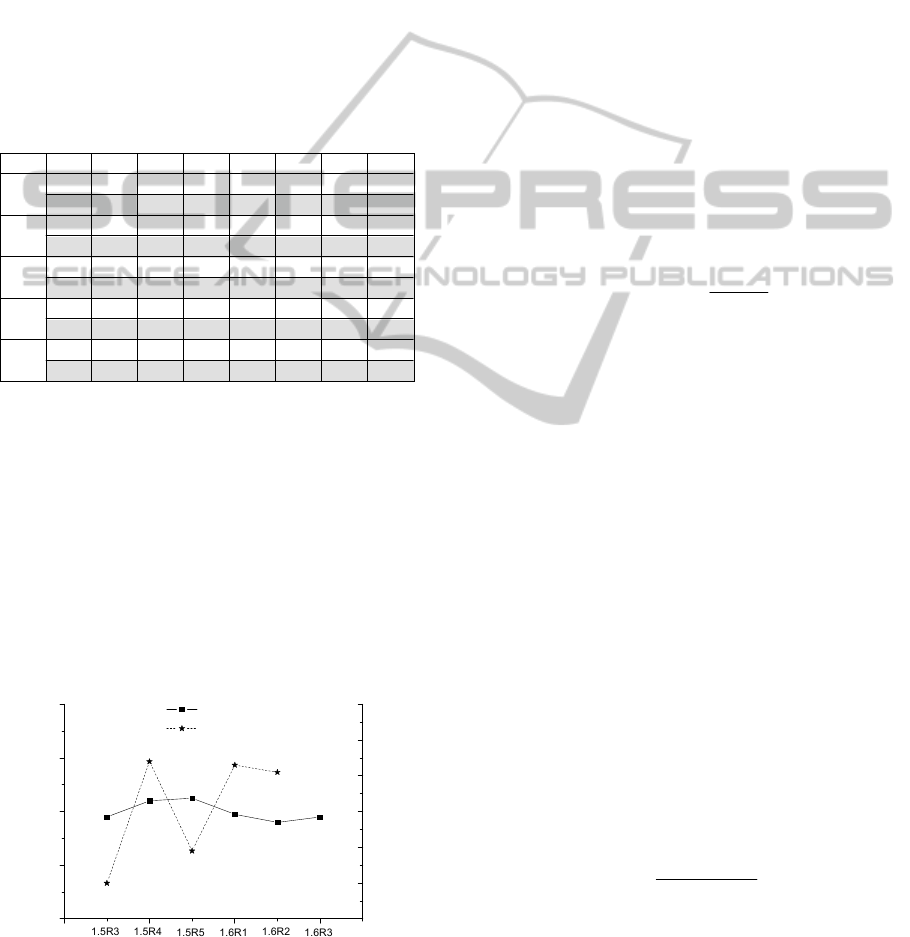
Figure 1: Number of classes and number of faulty classes

for core components of the chosen Rhino versions.

As we mainly focus on the fault data of Rhino’s core

components, the metric data were generated from

the same core components only. Table 1 presents the

descriptive statistics of predictive factors and Fig. 1

shows the number of classes and the number of

faulty classes reported for the core components of

the chosen Rhino’s versions.

3 MODELING TECHNIQUES

3.1 Logistic Regression

Logistic regression is a technique of probability

estimation based on maximum likelihood estimation.

In this model, let Y be the fault-proneness of a class

as the dependent variable (Y=1 indicating “faulty”

and Y=0 “fault-free”) and X

(i=1, 2, …, n) be the

predictive factors. LR assumes that Y follows a

Bernnouli distribution and the link function relating

and Y is the logit or log-odds:











),|1(

(1)

where X=(1, X

, X

, …, X

), β=(β

, β

, …, β

)

and β can be estimated by the maximum likelihood

estimator that would make the observed data most

likely (Hosmer and Lemeshow, 2000).

The LR curve between p and X

takes on an S

shape. When X

is not significant, the curve

approximates a horizontal line; conversely, the curve

presents a steep rise. This S shape is consistent with

the assumption about the empirical relationship

between predictors and the dependent variable

(Briand et al., 2000).

As shown in equation (1), LR assumes that the

predictive factors, X, are linearly and addictively

related to Y on a logistic scale. This may be too

simplistic and can introduce bias (Gokhale and Lyn,

1997). Further, LR uses only quantitative factors for

the prediction and constrains the inclusion of other

factors such as processing or external factors.

3.2 Naïve Bayes

The Bayes theorem is the theoretic foundation of the

naïve Bayes (NB) and also the Bayesian network:

)(

)()|(

)|(

CPCXP

XCP 

(2)

here C refers to the hypothesis (for the fault-

proneness prediction of a class, it denotes the

“faulty” or “fault-free” state of the class), X is the

evidence, i.e. the predictive factors. P(X) and P(C)

respectively refer to a prior probability of X and C.

Version

Items WMC DIT NOC CBO RFC LCOM

CCMAX

1.5R3

Mean 14.79 0.81 0.35 6.04 37.29 228.27 20.75

STDEV

19.55 0.84 1.29 7.24 47.13 811.40 43.88

1.5R4

Mean 14.76 0.85 0.32 6.08 26.91 236.45 21.58

STDEV

20.06 0.81 1.28 7.61 48.13 851.95 47.72

1.5R5

Mean 14.85 0.86 0.34 5.96 36.86 234.21 19.24

STDEV

19.93 0.85 1.34 6.84 47.68 914.97 42.29

1.6R1

Mean 15.53 0.82 0.33 6.12 38.87 300.16 20.50

STDEV

22.84 0.82 1.56 7.54 53.70

1475.65

44.82

1.6R2

Mean 15.84 0.73 0.34 6.33 39.64 303.44 20.77

STDEV

22.82 0.65 1.58 7.64 54.24

1482.48

46.25

100

120

140

160

Number of classes

Num of faulty classes

Number of classes

Number of faulty classes

118

116

119

125

124

118

Version

PredictingFault-pronenessofObject-OrientedSystemDevelopedwithAgileProcessusingLearnedBayesianNetwork

P(X|C) is the likelihood of X given C, and P(C|X) is

the posterior probability of C conditional to any

evidence, X.

Naïve Bayes is the simplest BN with a single

structure of a target node and multiple evidence

nodes (as shown in Figure 2) with the simplistic

assumption that the predictive factors are

conditionally independent given the class attribute

(C=“fault-free” or “faulty”, see the modeling

equation (3)).



1n



... ...

Figure 2: Naïve Bayes: the simplest BN.





CXP

XXCP )|(

)(

),,|(



(3)

If a predictive factor is continuous, the naïve

Bayes approach often assumes that within each class,

the numeric predictors are normally distributed

(Menzies et al., 2007). Such a distribution can be

represented in terms of its mean (μ) and standard

deviation (σ). Thus, we can estimate the probability

of an observed value from such estimates:

),;()|(

xgcCxXp





(4)

where

)(

))2/(1(),;(











exg

(5)

Equation 5 denotes the probability density

function (pdf) for a normal (Gaussian) distribution.

For the parameters (μ, σ) of the distribution of the

continuous metric predictor, we can use the

maximum likelihood estimates of the mean and

standard deviation (the sample average and the

sample standard deviation of the predictor within

each class).

The two assumptions of naïve Bayes, namely,

the conditional independence and the normal

distribution of continuous predictors, may not hold

for some domains (predictive metrics) (John and

Langley, 1995), thus affecting its prediction

performance.

3.3 Learned Bayesian Network

Different from the LR and NB models, Bayesian

network (BN) has a flexible network topology. We

can use techniques of data mining and optimization

to search for an optimal network and parameters to

generate a better model. Further, we can use optimal

discretization techniques to convert continuous

metrics into discrete inputs for the BN.

3.3.1 Basic Model

Definition 1. A Bayesian Network B over the set of

variables, V, is an ordered pair (B

, B

) such that

1. B

=G(V, E) is a directed acyclic graph, called the

network structure of B (

VVE 

is the set of

directed edges, representing the probabilistically

conditional dependence relationship between

random variable (rv) nodes that satisfies the

Markov property, i.e. there are no direct

dependency in B

which are not already

explicitly shown via edges, E) and

2. B

}|]1...0[:{ Vu













is a set of

assessment functions, where the state space Ω

the finite set of values for the variable u; π

is the

set of parent nodes of variables for u, indicated

by B

; if X is a set of variable, Ω

is the Cartesian

product of all state spaces of the variables in X;

uniquely defines the joint probability

distribution P(u|π

) of u conditional on its parent

set, π

Let c be the “FAULT” rv of a class and its state

space Ω

be binary, then Ω

={“faulty”, “faultless”}.

In a specified BN, if some evidences are given, we

can get the posterior probability or belief of

c=“faulty” as the fault-proneness by calculating the

marginal probability:







cuVu

ucuupcBel

),...,,...,,()"faulty"(

(6)

where







uin

upuup )|(),...,(



is the joint

probability over V.

In practice, we often use the efficient algorithm

of exact inference or approximate inference rather

than the marginalization of the joint probability to

compute Bel.

3.3.2 Optimal Discretization by Learning

According to Definition 1, we need to generate the

discrete state space Ω

of u as inputs to the BN when

the predictor u is continuous. As the predictive

factors used in our study are quantitative metrics,

discretization is necessary. There are two classes of

discretization methods: supervised and

unsupervised. Supervised methods can often achieve

a better result than unsupervised methods. Since we

have training instances with fault data, we use a

supervised method, the optimal multi-splits

algorithm proposed by Elomaa and Rousu (Elomaa

and Rousu, 1996), which is based on the information

theory. This algorithm finds the optimal cut-points

of a continuous predictor based on the

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

discretization’s contribution to the classification

prediction (“faulty” or “fault-free”). This algorithm

can achieve good splits with the optimal number of

numeric intervals adaptively adjusted, although we

need to set the maximum number of intervals

(Elomaa and Rousu, 1996).

The algorithm uses the following as the goodness

criterion:

( , 1, ) min ( ( 1,1, ) (1, 1, ) )

Impurity k i impurity k j impurity j i





(7)

where impurity(k, j, i) denotes the minimum

impurity that results when the training instances j

through i are partitioned into k intervals. The best k-

split is the one that minimizes impurity(k,1, N),

where N is the cardinality of the set of values of the

continuous predictor. The measure impurity (1, j+1,

i) is the average class entropy of the partition (the

conditional entropy given the partition). The

minimization of impurity makes minimum the

number of bits to encode the splits for the class

prediction, thus satisfying Occam's MDL principle

of the information theory (Elomaa and Rousu, 1996).

The algorithm is recursively run to identify the

optimal splits.

3.3.3 GA Learning of the Network Structure

There are two kinds of learning methods for a BN

structure: the conditional independence test and the

search of the scoring space. Since our goal is to

obtain a BN with the best performance, we prefer

the latter because it can generate a BN satisfying the

Markov property and has an optimal prediction

performance. In learning of an optimal BN, a quality

score is required to measure the network’s quality.

There are three kinds of score measures that bear a

close resemblance (Bouckaert, 1995): Bayesian

approach, information criterion approach, and

minimum description length approach. We used the

Bayesian approach that uses the posterior probability

of the learned network structure given the training

instances as a measure of the structure’s quality.

There are different algorithms for searching the

optimal Bayesian network. In our study, we used the

genetic algorithm (GA) because it can better explore

the search space and therefore has a lower chance of

getting stuck in local optima (Kabli et al., 2007). It is

more likely to find the globally optimal solution.

GA is based on the mechanics of natural

selection and genetics (“survival of the fittest”) and

it aims to find the optimum with structured yet

randomized information exchange among encoded

string structures. It evolves by repeating the

following steps: initialization or re-formation of the

population, evaluation and selection of individuals,

crossover and mutation for generation of offspring

until the maximum quality score is obtained or the

maximum evolution time is used up. To learn an

optimal BN, a connectivity matrix C=(c

)

i,j=1,…,n

used to encode the BN: if j is a parent node of i and

i>j, c

=1; otherwise, c

=0. Then the BN can be

represented by the string that consists of the

elements of C (Larranaga et al., 1996). The

inequality i>j ensures the assumed ancestral order

between the variables. Using the general GA for the

strings that encode the network structures, we can

find the optimal BN. For details of the algorithm, see

(Kabli et al., 2007; Larranaga et al., 1996).

In our study, the GA parameters were set as

follows: descendant population size=100, population

size=20, crossover probability=1, mutation

probability=0.1, random seed=1, and run time=50.

3.3.4 Learning of the Network Parameters

After the network structure is found, the conditional

probability table (CPT), i.e. implementation of

assessment functions in B

of the BN (Definition 1)

needs to be estimated from the database of instances.

We used the Bayesian estimator which assumes that

the conditional probability of each rv node

corresponding to its parent instantiation conforms to

the Dirichlet distribution (Korb and Nicholson,

2004) with local parameter independence:

),,,,(







with



being the hyperparameter

for state i.

The Dirichlet-based parameter estimator assumes

independence of local parameters which may not be

true in practice. This can result in biased parameters.

We can use the classification tree to improve the

learning while avoiding this assumption (Korb and

Nicholson, 2004).

3.3.5 Probabilistic Inference

The constructed BN model can be used to make an

inference of the probability prediction of the query

(target) variable (“faulty” or “fault-free”), given the

nodes of predictors. There are two kinds of

inference: exact inference and approximate

inference. Exact inference uses all the information of

nodes in the BN to make the probability inference. It

has a higher prediction accuracy than the

approximate inference, which makes the inference

through sampling (Korb and Nicholson, 2004). For a

large-scale connected BN, the exact inference is a

NP problem and the approximate inference is

preferred. But, in our study, as the learned network

PredictingFault-pronenessofObject-OrientedSystemDevelopedwithAgileProcessusingLearnedBayesianNetwork

is relatively simple (with less than 8 nodes), the

exact inference of the BN’s polytree (Korb and

Nicholson, 2004) is used, partly because it is more

efficient than the marginalization of the joint

probability.

4 DATA ANALYSIS

The data analysis mainly consists of four steps:

feature selection, multicollinearity analysis,

modeling and prediction, and evaluation.

4.1 Feature Selection

This step selects the correlative and informative

features (factors) for learning and prediction. As

Pearson’s correlation only measures the linear

correlation and may omit nonlinear information, we

use the information-based feature selector defined

by Quinlan (Quinlan, 1993): Information Gain Ratio

(GR). GR takes into account the information that

each feature contains and measures the gain ratio

given the feature to be assessed.

)(/))|()((),( fHfcHfHfcGR 

(8)

where H(c|f) is the conditional entropy of the target

class c given the feature f (MacKay, 2003).

If a predictor is continuous, it is necessary to

discretize the predictor. We used the algorithm

presented in section 3.3.2 to discretize the

continuous predictor before computing its GR

according to equation (8). Table 2 shows the GR of

the metrics used for each of the chosen Rhino

versions. CCMIN with GR of 0 will be removed

from the set of predictors.

Table 2: GR of C-K and Cyclomatic Complexity.

Metrics 1.5R3 1.5R4 1.5R5 1.6R1 1.6R2

WMC 0.23 0.21 0.14 0.23 0.26

DIT 0 0.09 0 0.18 0.12

CBO 0.36 0.24 0.13 0.22 0.20

RFC 0.49 0.24 0.22 0.30 0.26

LCOM 0.28 0.29 0.26 0.20 0.13

NOC 0 0.18 0 0 0

CCMIN 0 0 0 0 0

CCMAX 0.51 0.21 0.12 0.18 0.16

CCMEA N

0.29 0.18 0.12 0.17 0.12

CCSUM

0.11 0.22 0 0.16 0.13

4.2 Multicollinearity Analysis

For multicollinearity analysis, we can use the

combination of predictive factors with less

redundancy information for a better learning and

prediction for LR and NB. The variance inflation

factor (VIF) is often used to diagnose the

multicollinearity and weaken it (Dirk and Bart,

2004). If multicollinearity exists, by comparing the

Pearson’s correlation and removing one of the

strongly correlative independent variables, or

removing the predictor with the maximum VIF value,

the multicollinearity can be gradually weakened

until VIFs of all the predictors are equal to or

smaller than 3. We directly used the result of

multicollinearity analysis in (Olague et al., 2007)

since it analyzed the same system (Rhino) and

similar versions (1.5R3, 1.5R4 and 1.5R5) as ours.

Thus, two combinations of C-K metrics were chosen

as sets of predictive factors (with VIF<3):

 C-K model 1: CBO, DIT, LCOM, NOC, and

WMC;

 C-K model 2: CBO, DIT, LCOM, NOC, and

RFC.

For the cyclomatic complexity metrics, Table 2

shows that CCMAX has a larger GR for almost all

the Rhino versions, which indicates its higher

contribution to the prediction. Further, there are

large correlations between CCMAX, CCSUM and

CCMEAN (CCMIN is removed as its GR is 0).

Since we only need to select the one with a better

GR value as the predictor of complexity, we chose

CCMAX which also had a weak correlation with the

C-K metrics (as shown in Table 3). Thus, CCMAX

will be combined with those metrics in C-K model 1

and model 2 to generate new sets of predictors.

Table 3: CCMAX’s Correlation with CK-Metrics.

Version WMC DIT CBO RFC LCOM NOC

1.5R3 0.45* -0.21* 0.47* 0.56* 0.25* 0.22*

1.5R4 0.46* -0.09* 0.44* 0.57* 0.25* 0.04*

1.5R5 0.50* -0.07* 0.36* 0.55* 0.29* 0.023

1.6R1 0.46* -0.05 0.37* 0.53* 0.21* 0.072

1.6R2 0.47* 0 0.38* 0.54* 0.22* 0.074

*: Correlation is significant at the 0.01 level (2-tailed).

4.3 Modeling and Prediction

For LR and NB, we chose informative combinations

(Table 4) of predictive factors with less redundancy

information according to Table 2 and the above

multicollinearity analysis. As BN can model the

complex probabilistic dependent (conditional)

relationships between predictors with its flexible

network topology, we do not consider the

multicollinearity issue and choose all the predictors

with nonzero GR values.

The procedure of modeling and predictio

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

n follows the techniques described earlier in section

3. For the LR, the continuous product metrics are

directly used as inputs since its model (equation 1) is

based on continuous attributes; for the NB, we use

the pdf of a normal (Gaussian) distribution (equation

5) for estimation (equation 3). But for the BN, the

algorithm of section 3.3.2 is first used to discretize

the continuous predictors and then the modeling is

based on the discretized predictors and fault data.

Table 4: Combinations of predictors.

We evaluate the performance of these prediction

methods in two ways. The first method applied the

usual 10x10 cross-folder validation. In this

validation, the dataset was randomly divided into 10

buckets of equal size. 9 buckets were used for

training and the last bucket was used for the test.

The procedure was iterated 10 times and the final

result was averaged. For the construction of model,

we used all the instances for learning. The second

method used the prediction model of one version to

predict the fault-proneness of the relevant classes of

the next version (i.e. 1.5R3 for 1.5R4, 1.5R4 for

1.5R5, 1.5R5 for 1.6R1, and 1.6R1 for 1.6R2).

4.4 Evaluation Methods

We use the receiver operative characteristic (ROC)

as the evaluation method. ROC was originated from

the signal detection theory and statistical decision

theory. It assumes that the binary signal is corrupted

by Gaussian noise and the recognition accuracy

depends on the strength of signal, noise variance,

and desired hit rate or false alarm rate. We can set

different discrimination thresholds (p

) to test the

sensitivity of the recognition performance of the

learner for lowering the effect of noise variance.

ROC has been widely used in evaluation of binary

classifications as a relatively objective measure.

In a ROC graph, the horizontal axis represents 1-

specificity and the vertical axis the sensitivity. If we

signal (0 regarded as “fault-free” and 1 as “faulty”),

the 1-specificity refers to the ratio of the instances

detected as “faulty” among all the fault-free

instances (a.k.a.

probability of false alarms, pf) and

the sensitivity refers to the ratio of the instances also

detected as “faulty” among all the faulty instances

(a.k.a. probability of fault detection, pd). Precision

(p) is the proportion of the correctly predicted cases.

Table 5: A Confusion Matrix.

Predicted

fault-free faulty

Actual

fault-free

a b

faulty

c d

pd, pf, and precision can be calculated from the

confusion matrix (Table 5). The confusion matrix

contains information about actual and predicted

classifications from a learner. Each column of this

matrix represents the instances in a predicted class,

while each row represents the instances in an actual

class. From Table 5, we have:

pd=d/(c+d), pf= b/(a+b), p=d/(b+d)

As p is an unstable index for measuring the

prediction performance (Menzies et al., 2007b), we

regard it as a secondary reference.

According to the definition of pd and pf, their

range must be within the interval [0, 1]. A larger pd

with a lower pf indicates a good prediction

performance. When the ROC point (pf, pd) is closer

to the upper-left corner (0, 1), called “sweet spot”

where pf=0 and pd=1, the prediction model has a

better performance. Often we cannot simultaneously

achieve a high pd and low pf. The balance is based

on the Euclidean distance from the sweet spot (0,1)

to a pair of (pf, pd):

2/))1()0((1

 pdpfbalance

(9)

A higher balance indicates being closer to the

sweet spot and a better prediction performance.

ROC curve corresponds to a sensitivity analysis.

We can set different values of the threshold of the

fault-proneness, p

from 0 to 1, to calculate the

value pairs (pf, pd) for each threshold. Then we use

these pairs to construct a curve with pf varying from

0 to 1. If the curve is closer to the sweet spot and

more convex than another curve, then its

performance is better; if the curve is close to the

diagonal line from (0, 0) to (1, 1), its prediction

performance is no better than a random guess

(Heeger, 1998).

Version Method Combination of predictive factors

1.5R3

LR/NB

Model 1: CBO, LCOM, WMC, CCMAX

Model 2: CBO, LCOM, RFC, CCMAX

BN WMC, CBO, LCOM, RFC, CCMX

1.5R4

LR/NB

Model 1: CBO, DIT, LCOM, NOC, WMC, CCMAX

Model 2: CBO, DIT, LCOM, NOC, RFC, CCMAX

BN WMC, CBO, DIT, LCOM, NOC, RFC, CCMAX

1.5R5

LR/NB

Model 1: CBO, LCOM, WMC, CCMAX

Model 2: CBO, LCOM, RFC, CCMAX

BN WMC, CBO, LCOM, RFC, CCMX

1.6R1

LR/NB

Model 1: CBO, DIT, LCOM, WMC, CCMAX

Model 2: CBO, DIT, LCOM, RFC, CCMAX

BN WMC, CBO, DIT, LCOM, RFC, CCMAX

1.6R2

LR/NB

Model 1: CBO, DIT, LCOM, WMC, CCMAX

Model 2: CBO, DIT, LCOM, RFC, CCMAX

BN WMC, CBO, DIT, LCOM, RFC, CCMAX

PredictingFault-pronenessofObject-OrientedSystemDevelopedwithAgileProcessusingLearnedBayesianNetwork

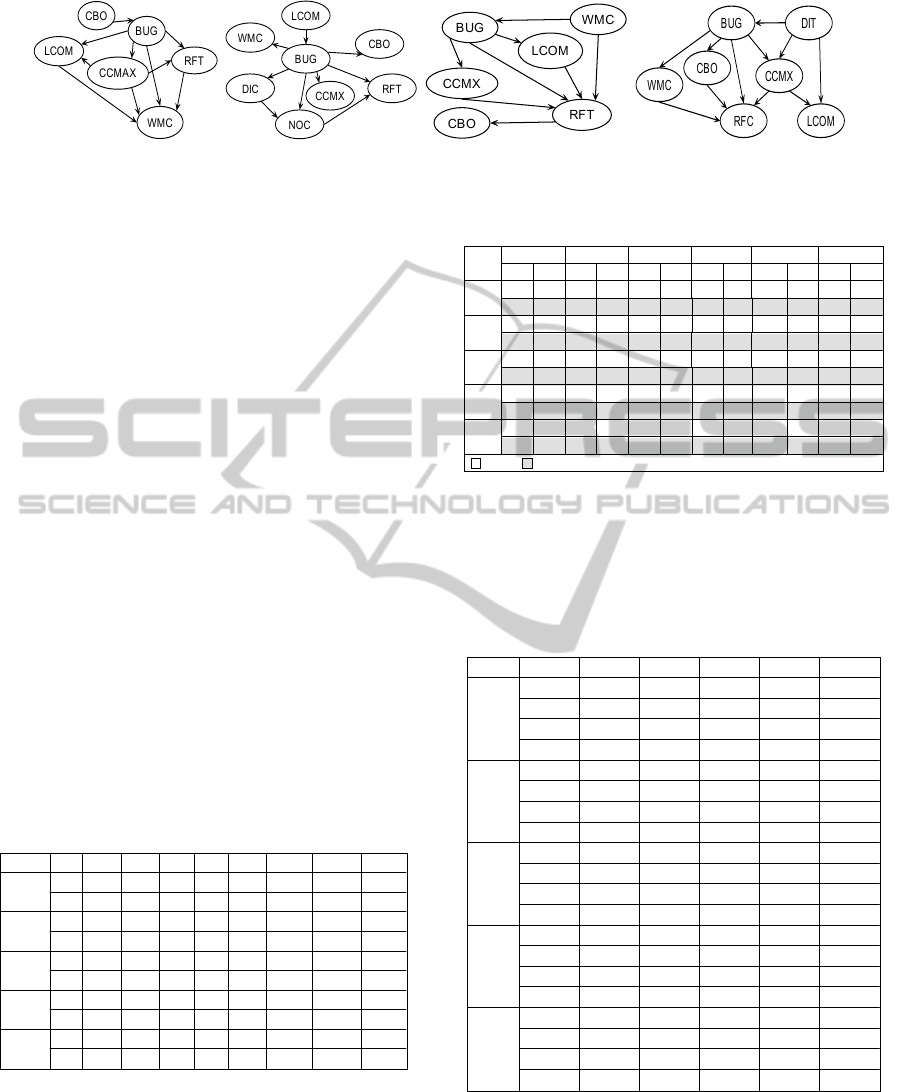
1.5R3 1.5R4 1.5R5 1.6R1

Figure 3: Network topologies of the learned BN for the chosen Rhino versions.

ROC area represents the area between the horizontal

axis and the ROC curve and it reflects the precision

of sensitivity analysis. Its value should be between

0.5 and 1. A value close to 0.5 indicates

completely invaluable, a value between 0.5 and 0.7

means lowly valuable, a value between 0.7 and 0.9

means moderately valuable, and a value above 0.9

indicates highly precise (Heeger, 1998).

5 RESULTS AND DISCUSSION

5.1 Learned Models

Table 6 lists the coefficients of model 1 and 2

learned by the LR. Our result shows that model 2 of

NB had a better performance than model 1. Thus, it

will be used for comparison against the LR and BN

models. Table 7 presents the parameters (mean and

standard deviation) of pdf for the “faulty” classes

(marked with 1) and “fault-free” classes (marked

with 0) of model 2 of the NB.

Figure 3 shows the network topology of the

learned BN for each of the four test versions (1.5R3,

1.5R4, 1.5R5, 1.6R1).

Table 6: Coefficients (β) Learned by LR.

Version

Model

WMC DIT NOC CBO RFC LCOM

CCMAX

Intercept

1.5R3

1 0.02 - - 0.05 - 0.000 0.02 -3.08

2 - - - 0.10 -0.01 0.002 0.02 -2.93

1.5R4

1 0.02 0.08 1.45 0.26 - 0.002 0.006 -2.4

2 - 0.04 1.46 0.22 0.02 -0.000 0.004 -2.32

1.5R5

1 0.06 - - 0.10 - -0.001 -0.004 -2.63

2 - - - 0.03 0.03 -0.001 -0.005 -2.40

1.6R1

1 0.03 -0.25 - 0.24 - -0.001 0.001 -1.67

2 - -0.26 - 0.20 0.02 -0.001 0 -1.00

1.6R2

1 0.03 -1.0 - 0.17 - -0.000 0.004 -1.57

2 - -1.09 - 0.09 0.03 -0.001 -0.00 -0.91

5.2 Comparison by Cross Validation

Table 8 gives the comparison of the prediction

models (LR, NB and BN) from the 10x10 cross-

folder validation. The BN achieves a better pd (0.55-

0.792) than the NB, LR-model 1 and LR-model 2 for

Table 7: Pdf’s Parameters for NB-Model 2.

the chosen Rhino versions (1.5R3, 1.5R4, 1.5R5,

1.6R1 and 1.6R2). Further, for each version, the

proposed BN keeps its pd above 0.5 which

demonstrates a high stability of prediction

performance.

Table 8: Comparison of the Models by Cross Validation.

Relatively, for the test versions, both LR and NB

have a lower and unstable pd value (the LR’s pd

ranges from 0.31 to 0.648 and the NB’s pd ranges

from 0.345 to 0.519). Also, the BN’s balance is

better and more stable than that of both LR and NB

although its precision is slightly lower than theirs.

Version

DIT NOC CBO RFC LCOM CCMAX

1 0 1 0 1 0 1 0 1 0 1 0

1.5R3

- - - -

13.44

4.48

90.58

25.9

1032.5

61.28 69.30 10.78

- - - -

12.13

4.62

73.65

29.23 1701.0

179.9 83.52 17.74

1.5R4

0.61 1.03 0.48 0.03

10.56

2.52

65.49

14.89 519.26

14.19 36.97

9.40

0.78 0.77 1.84 0.33 9.33 3.25

58.80

15.98 1232.1

58.78 58.82 32.11

1.5R5

- - - -

11.42

4.15

78.78

23.80

751.4

69.84 35.18 13.76

- - - - 9.93 4.59

67.24

29.80 1739.2

257.9 53.93 36.94

1.6R1

0.58 1.02 - - 9.75 2.90

63.67

19.13 599.43

40.11 30.68 12.26

0.90 0.69 - - 9.53 3.08

66.43

26.95 2154.1

239.1 51.81 36.60

1.6R2

0.49 0.92 - - 9.98 3.32

65.32

18.77 601.83

49.51 32.32 11.47

0.61 0.62 - - 9.83 3.34

68.33

25.29 2176.3

250.2

54.7

35.51

:mean; :standard deviation

Version Model pd pf

precision

ROC A rea

balance

1.5R3

LR-model1

0.4 0.031 0.727 0.784 0.399

LR-model2

0.4 0.031 0.727 0.755 0.399

NB-model2

0.55 0.061 0.647 0.778 0.546

BN 0.55 0.061 0.647 0.867 0.546

1.5R4

LR-model1

0.63 0.157 0.756 0.834 0.598

LR-model2

0.648 0.143 0.778 0.832 0.620

NB-model2

0.519 0.071 0.848 0.803 0.514

BN 0.722 0.129 0.813 0.89 0.694

1.5R5

LR-model1

0.276 0.052 0.615 0.756 0.274

LR-model2

0.31 0.052 0.643 0.767 0.308

NB-model2

0.345 0.063 0.625 0.697 0.342

BN 0.552 0.042 0.8 0.806 0.550

1.6R1

LR-model1

0.623 0.152 0.767 0.785 0.594

LR-model2

0.642 0.182 0.739 0.79 0.598

NB-model2

0.377 0.061 0.833 0.785 0.374

BN 0.792 0.242 0.724 0.84 0.681

1.5R2

LR-model1

0.627 0.231 0.681 0.796 0.561

LR-model2

0.609 0.185 0.721 0.804 0.567

NB-model2

0.392 0.046 0.87 0.77 0.390

BN 0.784 0.323 0.656 0.824 0.611

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

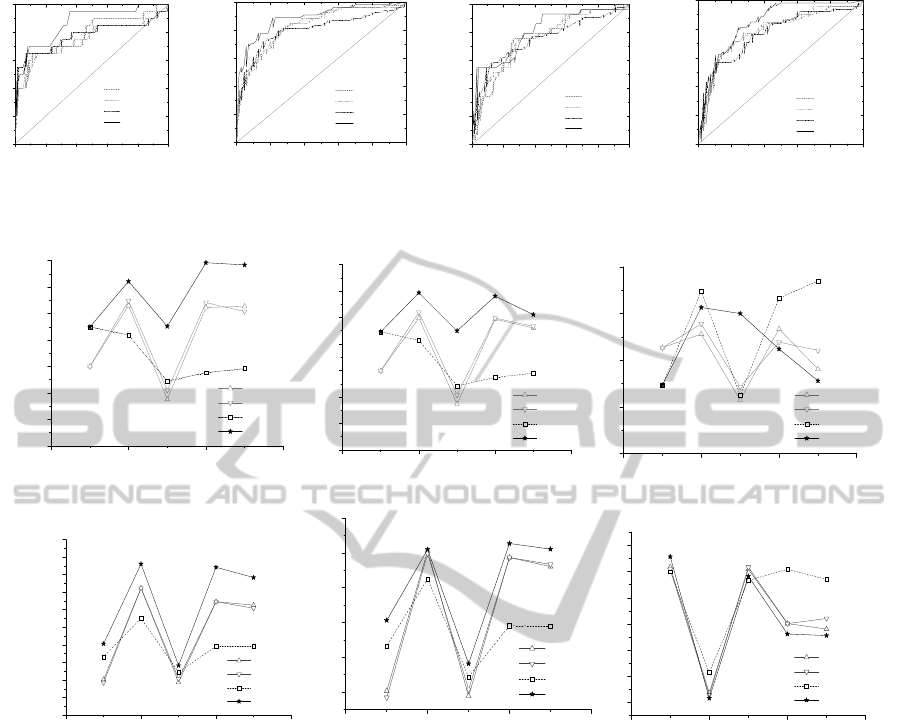
1.5R3 1.5R4 1.5R5 1.6R1

Figure 4: ROC curves of the prediction models (LR, NB and BN) for the chosen Rhino versions.

a) b) c)

d) e) f)

Figure 5: Changes of pd, balance and precision by the cross-validation (a, b, c) and the validations of continual versions (d,

e, f).

Figure 4 shows ROC curves of the prediction

models for the chosen Rhino versions. The ROC of

the BN is mostly closer to the sweet spot and more

convex than those of the LR or NB, which further

indicates its better performance.

5.3 Validation by Continual Versions

For the fault-proneness prediction, a better method

of validation is to use the prediction model learned

from one version to test the next version. This

validation by continual versions is more useful for

testing software developed with a highly-iterative or

agile evolutional strategy (Olague et al., 2007). We

used the models of LR-model 1, LR-model 2, NB-

model 2 and BN learned with the class instances of

the core components of one version to test those of

the next version with the same predictors (1.5R3 for

1.5R4, 1.5R4 for 1.5R5, 1.5R5 for 1.6R1 and 1.6R1

for 1.6R2). Table 9 shows the results.

For Rhino versions 1.5R3 and 1.5R5, all LR, NB

and BN models present a low pd and balance.

However, for these two versions, the BN has a

higher pd and balance than those of LR and NB. For

the other versions (1.5R4 and 1.6R1), the BN

achieves a much better pd and balance. The ROC

areas of all the models are above 0.7, indicating

moderate to high precision.

Figure 5 shows changes of pd, balance and

precision of the prediction models in the cross-folder

validation (a, b and c) and the validation of continual

versions (d, e and f). As seen in Figure 5a vs. 5d, 5b

vs. 5e, the pd and balance curves of the models keep

the same shape (two linked “V”) and trend. The

0.0 0.2 0.4 0.6 0.8 1.0

0.0

0.2

0.4

0.6

0.8

1.0

0.0 0.2 0.4 0.6 0.8 1.0

0.0

0.2

0.4

0.6

0.8

1.0

LR Model1

LR Model2

Sensitivity (pd)

1-Specificity (pf)

0.0 0.2 0.4 0.6 0.8 1.0

0.0

0.2

0.4

0.6

0.8

1.0

0.0 0.2 0.4 0.6 0.8 1.0

0.0

0.2

0.4

0.6

0.8

1.0

LR Model1

LR Model2

Sensitivity (pd)

1-Specificity (pf)

0.0 0.2 0.4 0.6 0.8 1.0

0.0

0.2

0.4

0.6

0.8

1.0

0.0 0.2 0.4 0.6 0.8 1.0

0.0

0.2

0.4

0.6

0.8

1.0

LR-Model1

LR-Model2

Sensitivity (pd)

1-Specificity (pf)

0.00.20.40.60.81.0

0.0

0.2

0.4

0.6

0.8

1.0

0.00.20.40.60.81.0

0.0

0.2

0.4

0.6

0.8

1.0

LR Model1

LR Model2

Sensitivity (pd)

1-Specificity (pf)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

LR-M1

LR-M2

Version

1.5R3

1.5R4

1.5R5

1.6R1

1.6R2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

LRm1

LRm2

Balance

Version

1.5R3

1.5R4 1.5R5

1.6R1

1.6R2

0.5

0.6

0.7

0.8

0.9

LRm1

LRm2

Precision

Version

1.5R3

1.5R4 1.5R5

1.6R1

1.6R2

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

Version

LR-M1

LR-M2

1.5R3

1.5R4

1.5R5

1.6R1

1.6R2

0.2

0.3

0.4

0.5

0.6

0.7

LRM1

LRM2

Balance

Version

1.5R3

1.5R4

1.5R5

1.6R1

1.6R2

0.4

0.5

0.6

0.7

0.8

0.9

1.0

Precision

LRm1

LRm2

Version

1.5R3

1.5R4 1.5R5

1.6R1

1.6R2

PredictingFault-pronenessofObject-OrientedSystemDevelopedwithAgileProcessusingLearnedBayesianNetwork

Table 9: Validation of the Models by Continual Versions.

Version Model pd pf

precision

ROC A rea

balance

1.5R3

LR-model1

0.204 0.014 0.917 0.842 0.204

LR-model2

0.185 0.014 0.909 0.847 0.185

NB-model2

0.333 0.029 0.9 0.779 0.332

BN 0.407 0.014 0.957 0.79 0.407

1.5R4

LR-model1

0.724 0.281 0.438 0.795 0.606

LR-model2

0.724 0.292 0.429 0.795 0.598

NB-model2

0.552 0.156 0.516 0.745 0.526

BN 0.862 0.365 0.417 0.806 0.610

1.5R5

LR-model1

0.189 0.015 0.909 0.822 0.189

LR-model2

0.208 0.015 0.917 0.825 0.208

NB-model2

0.245 0.03 0.867 0.78 0.244

BN 0.283 0.03 0.882 0.758 0.282

1.6R1

LR-model1

0.647 0.215 0.702 0.816 0.587

LR-model2

0.647 0.215 0.702 0.827 0.587

NB-model2

0.392 0.031 0.909 0.818 0.391

BN 0.843 0.338 0.662 0.832 0.627

difference in shape between the pd and balance

curves is not large. Further, the core components of

Rhino version 1.5R5 have the worst prediction

performance either by the cross-folder validation or

the validation of continual versions. According to

the change log of Rhino (Bugzilla, 2005), since

version 1.6R1, there was a major revision (to

support ECMAScript for XML (E4X) as specified

by ECMA 357 standard) which represents a large

change from the earlier versions. This additional

functionality (non-fault cause) may result in the low

pd and balance of the models for this version 1.5R5

when making prediction for the next version, 1.6R1

(Figure 5d and 5e).

As can be seen in Figure 5 (5a vs. 5d, 5b vs. 5e),

the performance of the prediction models (LR-model

1, LR-model 2, NB-model 2 and BN) by the cross-

folder validation is similar to that by the validation

of continual versions. Overall, the performance by

the cross-folder validation is slightly better than that

by the continual validation but for the BN model,

this is not the case for version 1.5R4 and 1.6R1.

Further, the difference in performance of the

prediction models between the cross-folder

validation and the validation of continual versions is

similar. The BN has achieved a better prediction

performance (a larger pd and balance) for each of

the chosen Rhino versions either by the cross-folder

validation or by the validation of continual versions.

The performance of the NB and LR models is

inconsistent (for version 1.5R3 and 1.5R5, NB is

better than LR; but for version 1.5R4 and 1.6R1, LR

is better than NB).

On the other hand, the precision curves of the

prediction models present an unstable trend either by

the cross-folder validation (Figure 5c) or by the

validation of continual versions (Figure 5f). There is

no one model whose precision always keeps a better

value across the releases of the continual versions.

Our analysis suggests that precision is not a good

measure for evaluation of the prediction models due

to its large standard deviations (unstablility)

(Menzies et al., 2007b). Although the BN’s

precision is sometimes not as good as the LR or NB,

it’s larger and more stable pd and balance show that

it is valuable for fault-proneness prediction.

6 CONCLUSIONS

This paper presents a learned BN that is based on the

data mining techniques (i.e. the optimal

discretization and the genetic algorithm) for the

prediction of fault-proneness of the agile OO

systems. D'Ambros et al. (D'Ambros et al., 2012)

illustrated the importance of predictors and Menzies

et. al. (Menzies et al., 2007) showed the importance

of learners such as naïve Bayes. We extended the

previous work by illustrating the improvement of

fault-proneness prediction by learning algorithms for

feature selection and flexible network structure.

Using the continual versions of the open-source

system Rhino, we empirically validated the proposed

prediction model and compare its performance with

LR and NB.

The BN has the advantages of a flexible network

structure and wide choices of the learning and

optimization algorithms. It also avoids the

constraints of LR (logistical-scale linear and

addictive relationships between predictors and the

dependent variable (fault-proneness)), and the

assumptions of NB (the conditional independence

and the normal distributions of predictors). Based on

the 10х10 cross-validation and the validation of

continual versions of the test system, the prediction

results of the BN learned by the GA are positively

encouraging: compared with the NB and LR, the BN

has a better and stable pd and balance. The

comparison between the ROC curves (Figure 4) of

the prediction models also strengthened this

conclusion.

In the previous studies on using BN for fault-

proneness, Liu et al. (Liu et al., 2008 ) used

spanning tree to construct their BN, Fenton et al.

(Fenton et al., 2008) constructed the network based

on the domain knowledge, and Pai and Dugan (Pai

and Dugan, 2007) used LR to construct and

parameterize their BN model. Compared with the

previous studies, we adopted optimal discretization

and genetic algorithm (GA) to improve the network

(avoiding missing of domain knowledge for

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

construction of network and local optimization since

GA is a globally optimal solution).

By the validation of continual versions, the

learned BN method is particularly valuable for the

quality evaluation of the OO systems developed with

the highly-iterative or agile strategy.

There are several threats to validity. The first

threat is that only version series of one software

product (Rhino) were used to train and test the

model. But the paper’s focus is on examination of

the learners in agile process software (not

generalization of the method to general software

modules). We have examined our models across

other different software products and statistically

demonstrated our approach’s advantages in a

previous study (Li and Leung, 2011). The second

threat is that selection of different predictive factors

for different models may damage the validity of the

models. But learning was conducted to get the

optimal prediction performance. Using the same

methods of feature selection and optimal learning

algorithms for different models, the prediction

performance of the models could be comparable no

matter what different predictors were used.

In the future, we will explore the following aspects:

 Using additional benchmark datasets (Basili et

al., 1996; Menzies et al., 2007; Pai and Dugan,

2007) from public domain, we will conduct more

empirical validation of the BN in comparison

with other models for the fault-proneness

prediction. This can determine the superiority

and stability of BN for the quality assessment of

agile software.

 Given the many data mining and optimization

algorithms, we will explore the effects of

different algorithms on the prediction.

 We will investigate the applicability of BN for

the prediction of other aspects (e.g. reliability) of

software quality, using additional metrics (e.g.

slice-based cohesion and coupling) and

qualitative factors.

ACKNOWLEDGEMENTS

This research is partly supported by the Hong Kong

CERG grant PolyU5225/08E, NSFC grant

1171344/D010703, MOST grants (2012CB955503

and 2011AA120305–1).

REFERENCES

Ambler, S. W., R., J., 2002. Agile Modeling: Effective

Practices for Extreme Programming and the Unified

Process. John Wiley & Sons.

Basili, V. R., Briand, L. C., Melo, W. L., 1996. A

validation of object-oriented design metrics as quality

indicators. IEEE Transactions on Software

Engineering 22, 751-761.

Bouckaert, R. R., 1995. Bayesian Belief Network: from

Construction to Inference.

Boyd, N., 2007. Rhino home page.

Briand, L. C., Wust, J., Daly, J. W., Porter, D. V., 2000.

Exploring the relationships between design measures

and software quality in object-oriented systems.

Journal of Systems and Software 51, 245-273.

Bugzilla, D., 2005. Mozilla Foundation.

Cardoso, J., 2006. Process Control-flow Complexity

Metric: An Empirical Validation, IEEE International

Conference on Services Computing (IEEE SCC 06).

IEEE Computer Society, Chicago, pp. 167-173.

Chidamber, S. R., Kemerer, C. F., 1994. A metrics suite

for object-oriented design IEEE Transactions on

Software Engineering 20, 476-493.

Cohn, C., 2006 Agile Alliance Home Page.

CYVIS, 2007. CYVIS.

D'Ambros, M., Lanza, M., Robbes, R., 2012. Evaluating

defect prediction approaches: a benchmark and an

extensive comparison. Empirical Software

Engineering 17, 531-577.

Dirk, V. P., Bart, L., 2004. Customer Attrition Analysis

for Financial Services Using Proportional Hazard

Models. European Journal of Operational Research

157, 196-127.

Elomaa, T., Rousu, J., 1996. Finding optimal multi-splits

for numerical attributes in decision tree learning,

ESPRIT Working Group, NeuroCOLT Technical

Report Series, pp. 1-16.

Fenton, N., Neil, M., Marsh, W., Hearty, P., Radlinski, L.,

Krause, P., 2008. On the effectiveness of early life

cycle defect prediction with Bayesian nets Empirical

Software Engineering 13, 499-537.

Gokhale, S. S., Lyn, M. R., 1997. Regression tree

modeling for the prediction of software quality, Proc.

Of Third ISSAT Intl. Conference on Reliability,

Anaheim, CA, pp. 31-36.

Guo, L., Ma, Y., Cukic, B., Singh, H., 2004. Robust

prediction of faultproneness by random forests, the

15th International Symposium on Software Reliability

Engineering. IEEE Computer Society, Washington,

DC, pp. 417- 428.

Harrison, R., Counsell, S., Nithi, R., 1998. An Evaluation

of the MOOD Set of Object Oriented Software Metrics.

IEEE Transaction on Software Engineering 24, 150-

157.

Heeger, D., 1998. Signal Detection Theory.

Herbsleb, J. D., 2001. Global software development. IEEE

Software 18, 16-20.

Hosmer, D., Lemeshow, S., 2000. Applied Logistic

Regression, 2 ed. John Wiley and Sons.

PredictingFault-pronenessofObject-OrientedSystemDevelopedwithAgileProcessusingLearnedBayesianNetwork

John, G. H., Langley, P., 1995. Estimating continuous

distributions in Bayesian classifiers, the Eleventh

Conference on Uncertainty in Artificial Intelligence,

San Mateo, pp. 338-346.

Kabli, R., Herrmann, F., McCall, J., 2007. A Chain-Model

Genetic Algorithm for Bayesian Network Structure

Learning, GECCO, London.

Korb, K. B., Nicholson, A. E., 2004. Bayesian Artificial

Intelligence. Chapman & Hall/CRC.

Larranaga, P., Murga, R., Poza, M., Kuijpers, C., 1996.

Structure Learning of Bayesian Network by Hybrid

Genetic Algorithms, in: Fisher, D., Lenz, H.J. (Eds.),

Learning from Data: AI and Statistics. Springer-

Verglag.

Li, L., Leung, H., 2011. Mining Static Code Metrics for a

Robust Prediction of Software Defect-Proneness,

ACM /IEEE International Symposium on Empirical

Software Engineering and Measurement Aneheim, CA

Liu, Y., Cheah, W., Kim, B., Park, H., 2008 Predict

softare failure-prone by learning bayesian network

International Journal of Advanced Science and

Technology 1, 33-42.

MacKay, D., 2003. Information Theory, Inference and

Learning Algorithms. Cambridge University Press.

McCabe, T. J., 1976. A complexity measure. IEEE

Transactions on Software Engineering 2, 308 - 320.

Menzies, T., Dekhtyar, A., Distefano, J., Greenwald, J.,

2007b. Problems with precision: a response to

"comments on 'data mining static code attributes to

learn defect predictors'". IEEE Transactions on

Software Engineering 33, 637-640.

Menzies, T., Greenwald, J., Frank, A., 2007. Data mining

static code attributes to learn defect predictors. IEEE

Transactions on Software Engineering 33, 2-13.

Olague, H. M., Etzkorn, L. H., Gholston, S., Quattlebaum,

S., 2007. Empirical validation of three software

metrics suites to predict fault-proneness of object-

oriented classes developed using highly iterative or

agile software development processes. IEEE

Transactions on Software Engineering 33, 402-419.

Pai, G. J., Dugan, J. B., 2007. Empirical analysis of

software fault content and fault proneness using

Bayesian methods. IEEE Transactions on Software

Engineering 33, 675-686.

Quinlan, J. R., 1993. C4.5: Programs for Machine

Learning. Morgan Kauffman.

Singh, Y., Kaur, A., Malhotra, R., 2008. Predicting

software fault proneness model using neural network

Lecture Notes in Computer Science 5089, 204-214.

Singh, Y., Kaur, A., Malhotra, R., 2009. Software fault

proneness prediction using support vector machines,

Proceedings of the World Congress on Engineering

London, UK.

Singh Y., Kaur, A., Malhotra, R., 2009. Application of

Decision Trees for Predicting Fault Proneness,

International Conference on Information Systems,

Technology and Management-Information Technology,

Ghaziabad, India.

Spinellis, D., 2006. Code Quality: The Open Source

Perspective. Addison Wesley.

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems