
A Faster Algorithm for Checking the Dynamic Controllability
of Simple Temporal Networks with Uncertainty
Luke Hunsberger
Computer Science Department, Vassar College, Poughkeepsie, NY, 12604-0444, U.S.A.
Keywords:
Temporal Networks, Uncertainty, Dynamic Controllability.
Abstract:
A Simple Temporal Network (STN) is a structure containing time-points and temporal constraints that an agent
can use to manage its activities. A Simple Temporal Network with Uncertainty (STNU) augments an STN to
include contingent links that can be used to represent actions with uncertain durations. The most important
property of an STNU is whether it is dynamically controllable (DC)—that is, whether there exists a strategy
for executing its time-points such that all constraints will necessarily be satisfied no matter how the contingent
durations happen to turn out (within their known bounds). The fastest algorithm for checking the dynamic
controllability of STNUs reported in the literature so far is the O(N
4
)-time algorithm due to Morris. This
paper presents a new DC-checking algorithm that empirical results confirm is faster than Morris’ algorithm, in
many cases showing an order of magnitude speed-up. The algorithm employs two novel techniques. First, new
constraints generated by propagation are immediately incorporated into the network using a technique called
rotating Dijkstra. Second, a heuristic that exploits the nesting structure of certain paths in the STNU graph is
used to determine a good order in which to process the contingent links during constraint propagation.
1 INTRODUCTION
An intelligent agent needs to be able to plan, sched-
ule and manage the execution of its activities. Invari-
ably, those activities are subject to a variety of tem-
poral constraints, such as release times, deadlines and
precedence constraints. In addition, in some domains,
the agent may control the starting times for actions,
but not their durations (Chien et al., 2002; Hunsberger
et al., 2012). For a simple example, I may control the
starting time for my taxi ride to the airport, but not its
duration. Although I may know that the ride will last
between 15 and 30 minutes, I only discover the ac-
tual duration in real time, when I arrive at the airport.
Thus, if I need to ensure that I arrive at the airport no
later than 10:00, I must start my taxi ride no later than
9:30, in case the ride happens to last 30 minutes. In
more complicated examples involving large numbers
of actions with uncertain durations, generating a suc-
cesful execution strategy becomes more challenging.
A Simple Temporal Network with Uncertainty
(STNU) is a data structure that an agent can use to
support the planning, scheduling and executing of its
activities, some of which may have uncertain dura-
tions (Morris et al., 2001). The most important prop-
erty of an STNU is whether it is dynamically con-
trollable (DC)—that is, whether there exists a strat-
egy for executing the constituent actions such that
all temporal constraints are guaranteed to be satis-
fied no matter how the uncertain action durations hap-
pen to turn out in real time. Algorithms for deter-
mining whether STNUs are dynamically controllable
are called DC-checking algorithms. The fastest DC-
checking algorithm reported so far in the literature is
Morris’ O(N
4
)-time algorithm, where N is the num-
ber of time-points in the network (Morris, 2006).
For any given STNU, a DC-checking algorithm
only determines whether a dynamic execution strat-
egy exists for that network. However, if the network
is DC, then the information computed by the DC-
checking algorithm—which is collected into the so-
called AllMax matrix—can be used to incrementally
construct the desired execution strategy, one decision
at a time. In particular, after each execution event,
the AllMax matrix is updated and then used to gener-
ate the next execution decision. The computations re-
quired to incrementally generate an execution strategy
in this way can be done in O(N
3
) time (Hunsberger,
2013a). However, those computations cannot begin
until after the DC-checking algorithm produces the
AllMax matrix. Thus, DC-checking algorithms are of
central importance for STNUs.
63
Hunsberger L..
A Faster Algorithm for Checking the Dynamic Controllability of Simple Temporal Networks with Uncertainty.
DOI: 10.5220/0004758100630073
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 63-73
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Y
3
X
−2
−5
10
A
C
Y
3
X
−2
−5
−2
8
10
A
C
Figure 1: The graph for the STN discussed in the text.
This paper presents a new DC-checking algorithm
that empirical results confirm is faster than Morris’
DC-checking algorithm, in many cases showing an
order of magnitude speed-up. The algorithm em-
ploys two novel techniques. First, new constraints
generated by propagation are immediately incorpo-
rated into the network using a technique called ro-
tating Dijkstra. Second, a heuristic that exploits the
nesting structure of certain paths in the STNU graph
is used to determine a good order in which to carry
out the propagation of constraints.
2 BACKGROUND
This section presents relevant background about Sim-
ple Temporal Networks (STNs) and Simple Tempo-
ral Networks with Uncertainty (STNUs). The presen-
tation highlights the strong analogies between STNs
and STNUs, culminating in the analogous Fundamen-
tal Theorems that explicate the relationships between
an STN/STNU, its associated graph, and its associ-
ated shortest-paths matrix.
2.1 Simple Temporal Networks
A Simple Temporal Network is a pair, (T , C), where
T is a set of real-valued variables called time-points,
and C is a set of binary constraints of the form,
Y − X ≤ δ, where X,Y ∈ T and δ ∈ R (Dechter et al.,
1991). An STN is called consistent if it has a solution
(i.e., a set of values for the time-points that jointly sat-
isfy the constraints). Consider the STN defined by:
• T = {A,C, X ,Y }
• C = {(C − A ≤ 10), (A −C ≤ −5),
(C −Y ≤ 3), (X −C ≤ −2)}
It is consistent since, for example, it has the following
solution: {(A = 0), (C = 6), (X = 3), (Y = 4)}.
STN Graphs. Each STN, S = (T , C ), has an asso-
ciated graph, G = hT , Ei, where the time-points in T
serve as the nodes for the graph, and the constraints
in C correspond one-to-one to its edges. In particular,
each constraint, Y − X ≤ δ, in C corresponds to an
edge, X
δ
Y , in E. The graph for the STN above is
shown on the lefthand side of Fig. 1. For convenience,
the constraints and edges associated with an STN are
called ordinary constraints and ordinary edges.
Each path in an STN graph, G, corresponds to a
constraint that must be satisfied by any solution for
the associated STN, S. In particular, if P is a path
from X to Y of length |P | in G, then the constraint,
Y − X ≤ |P |, must be satisfied by any solution to S.
For example, in the STN from Fig. 1, the path from
Y to C to A of length −2 represents the constraint,
A −Y ≤ −2 (i.e., Y ≥ A + 2). The righthand graph in
Fig. 1 includes a dashed edge from Y to A that makes
this constraint explicit. Note that this derived con-
straint is satisfied by the solution given earlier. Simi-
lar remarks apply to the edge from A to X.
Due to these sorts of connections, the all-pairs,
shortest-paths (APSP) matrix—called the distance
matrix, D—plays an important role in the theory of
STNs. In fact, the Fundamental Theorem of STNs
states that the following are equivalent: (1) S is con-
sistent; (2) each loop in G has non-negative length;
and (3) D has only non-negative entries down its main
diagonal (Dechter et al., 1991; Hunsberger, 2013a).
2.2 STNs with Uncertainty
A Simple Temporal Network with Uncertainty aug-
ments an STN to include a set, L, of contingent
links that represent temporal intervals whose dura-
tions are bounded but uncontrollable (Morris et al.,
2001). Each contingent link has the form, (A, x, y,C),
where A,C ∈ T and 0 < x < y < ∞. A is called the
activation time-point; C is the contingent time-point.
Although the link’s duration, C − A, is uncontrollable,
it is guaranteed to lie within the interval, [x, y]. When
an agent uses an STNU to manage its activities, con-
tingent links typically represent actions with uncer-
tain durations. The agent may control the action’s
starting time (i.e., when A executes), but only ob-
serves, in real time, the action’s ending time (i.e.,
when C executes).
1
For example, consider the STNU defined by:
• T = {A,C, X ,Y }
• C = {(C −Y ≤ 3), (X −C ≤ −2)}
• L = {(A, 5, 10,C)}
It is similar to the STN seen earlier, except for one
important difference. In the STN, the duration, C − A,
was constrained to lie within the interval [5, 10], but
the agent was free to choose any values for A and C
that satisfied that constraint. In contrast, in the STNU,
1
Agents are not part of the semantics of STNUs. They
are used here only for expository convenience.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
64

C − A is the duration of a contingent link. This dura-
tion is guaranteed to lie within [5, 10], but the agent
does not get to choose this value. For example, if A is
executed at 0, then the agent only gets to observe the
execution of C when it happens, sometime between 5
and 10. In this sense, the contingent duration is un-
controllable, but bounded.
Dynamic Controllability. For an STNU,
(T , C , L), the most important property is whether it
is dynamically controllable (DC)—that is, whether
there exists a strategy for executing the controllable
(i.e., non-contingent) time-points in T such that all
constraints in C are guaranteed to be satisfied no
matter how the durations of the contingent links
in L turn out in real time—within their specified
bounds (Morris et al., 2001). Such strategies, if
they exist, are called dynamic execution strategies—
dynamic in that their execution decisions may depend
on the observation of past execution events, but not
on advance knowledge of future events.
It is not hard to verify that the following is a dy-
namic execution strategy for the sample STNU.
Execute A at 0; and execute X at 3.
If C executes before time 7, then execute Y at time
C + 1; otherwise, execute Y at 7.
Thus, the sample STNU is dynamically controllable.
This strategy is dynamic in that the decision to exe-
cute Y depends on observations about C.
STNU Graphs. Each STNU, (T , C , L), has an as-
sociated graph, hT , E
+
i, where the time-points in T
serve as the nodes in the graph; and the constraints
in C and the contingent links in L together give rise
to the edges in E
+
(Morris and Muscettola, 2005). To
capture the difference between constraints and con-
tingent links, the edges in E
+
come in two varieties:
ordinary and labeled. As with an STN, each con-
straint, Y − X ≤ δ, in C corresponds to an ordinary
edge, X
δ
Y , in E
+
. In addition, each contingent
link, (A, x, y,C), in L gives rise to two ordinary edges
that together represent the constraint, C − A ∈ [x, y].
Finally, each contingent link, (A, x, y,C), also gives
rise to the following labeled edges:
• a lower-case edge, A
c:x
C, and
• an upper-case edge, A
C:−y
C.
The lower-case (LC) edge represents the uncontrol-
lable possibility that the duration, C − A, might as-
sume its lower bound, x. The upper-case (UC) edge
represents the uncontrollable possibility that C − A
might assume its upper-bound, y. The graph for the
sample STNU is shown on the lefthand side of Fig. 2.
C
A
Y
3
X
−2
−5
10
c : 5
C : −10
C
A
Y
3
X
−2
−5
10
3
C : −7
c : 5
C : −10
Figure 2: The graph for the sample STNU before (left) and
after (right) generating new edges.
Table 1: Edge-generation rules for STNUs.
(No Case) A
x
C
y
D adds: A
x+y
D
(Lower Case) A
x
C
c:y
D adds: A
x+y
D
(Upper Case) A
B:x
C
y
D adds: A
B:x+y
D
(Cross Case) A
B:x
C
c:y
D adds: A
B:x+y
D
(Label Rem.) B
b:x
A
B:z
C adds: A
z
C
Edge Generation for STNUs. Because the labeled
edges in an STNU graph represent uncontrollable
possibilities, edge generation (equiv., constraint prop-
agation) for STNUs is more complex than for STNs.
In particular, a variety of rules are required to handle
the interactions between different kinds of edges.
Table 1, below, lists the edge-generation rules
for STNUs given by Morris and Muscettola (2005).
2
The No Case rule encodes ordinary STN con-
straint propagation. The Lower Case rule generates
edges/constraints that guard against the possibility of
a contingent link taking on its minimum duration.
The Upper Case rule generates edges/constraints that
guard against the possibility of a contingent link tak-
ing on its maximum duration. The Cross Case rule
addresses the interaction of LC and UC edges from
different contingent links. Note that the rules gener-
ate only ordinary or upper-case edges.
The rules are sound in the sense that the edges
they generate correspond to constraints that must be
satisfied by any dynamic execution strategy. Gen-
erated upper-case edges represent conditional con-
straints. For example, Y
C:−2
A represents a con-
ditional constraint that can be glossed as, “While (the
contingent time-point) C remains unexecuted, Y must
wait at least 2 units after the execution of A.”
To illustrate these rules, consider the righthand
graph in Fig. 2. For ease of exposition, assume that
2
The rules are shown using Morris and Muscettola’s no-
tation. Note that: the x’s and y’s here are not necessarily
bounds for contingent links; C is only required to be con-
tingent in the Lower Case and Cross Case rules, where its
activation time-point is D and its lower bound is y; and in
the Upper Case and Cross Case rules, B is contingent, with
activation time-point A. The Lower Case rule only applies
when x ≤ 0 and A 6= C; the Cross Case rule only when x ≤ 0
and B 6= C; and the Label Removal rule only when z ≥ −x.
AFasterAlgorithmforCheckingtheDynamicControllabilityofSimpleTemporalNetworkswithUncertainty
65

e
e
2
e
1
P
P
0
Figure 3: Path transformation in an STNU graph.
A is executed at 0. The edge, C
−2
X, represents
the constraint, X − C ≤ −2 (i.e., X ≤ C − 2), which
requires X to be executed before the contingent time-
point C. To ensure that this constraint will be satisfied
even if C eventually happens to execute at its mini-
mum value of 5, X must be executed no later than 3
units after A, whence the dashed edge from A to X .
This dashed edge can be generated by applying the
Lower Case rule to the path from A to C to X.
Next, consider the edge, Y
3
C, which repre-
sents the constraint, C −Y ≤ 3 (i.e., Y ≥ C−3). To en-
sure that this constraint is satisfied, the following con-
ditional constraint must be satisfied: While C remains
unexecuted, Y must occur at or after 7. This con-
ditional constraint—called a wait—effectively guards
against C taking on its maximum value, 10. It is rep-
resented by the upper-case edge, Y
C:−7
A. This
edge can be generated by applying the Upper Case
rule to the path from Y to C to A.
It is not hard to verify that the constraints corre-
sponding to these generated edges are satisfied by the
sample dynamic execution strategy given earlier.
Semi-reducible Paths. Recall that each path in an
STN graph corresponds to a constraint that must be
satisfied by any solution for the associated STN. In
STNU graphs, it is the semi-reducible paths—defined
below—that correspond to the (possibly conditional)
constraints that must be satisfied by any dynamic ex-
ecution strategy for the associated STNU (Morris,
2006). Whereas an STN is consistent if and only if
its graph has no negative-length loops, an STNU is
dynamically controllable if and only if its graph has
no semi-reducible negative-length loops.
Before defining semi-reducible paths, it is useful
to view the edge-generation rules from Table 1 as
path-transformation rules, as follows. Suppose e
1
and
e
2
are consecutive edges in a path P , and that one of
the first four rules can be applied to e
1
and e
2
to gener-
ate a new edge e, as illustrated in Fig. 3. Further, let P
0
be the path obtained from P by replacing the edges,
e
1
and e
2
, with e. We say that P has been transformed
into P
0
. Similar remarks apply to the Label Removal
rule, which operates on a single edge.
A path in an STNU graph is called semi-reducible
if it can be transformed into a path that has only
ordinary or upper-case edges (Morris, 2006). The
soundness of the edge-generation rules ensures that
the constraints represented by semi-reducible paths
must be satisfied by any dynamic execution strat-
egy. Since shorter paths correspond to stronger con-
straints, the all-pairs, shortest-semi-reducible-paths
(APSSRP) matrix, D
∗
, plays an important role in the
theory of STNUs. In fact, the Fundamental Theo-
rem of STNUs states that the following are equivalent
for any STNU S: (1) S is dynamically controllable;
(2) every semi-reducible loop in its associated graph
has non-negative length; and (3) its APSSRP matrix,
D
∗
, has only non-negative entries along its main di-
agonal (Morris, 2006; Hunsberger, 2013b).
2.3 DC-Checking Algorithms
Algorithms for determining whether STNUs are dy-
namically controllable are called DC-checking al-
gorithms. The fastest DC-checking algorithm re-
ported so far is the O(N
4
)-time algorithm due to Mor-
ris (2006). Given an STNU graph G, Morris’ algo-
rithm uses the edge-generation rules from Table 1 to
generate new edges. Each newly generated edge is
added not only to G, but also, in a stripped down form,
to a related STN graph, called the AllMax graph. If the
AllMax graph ever exhibits a negative-length loop, the
original STNU is declared to be non-DC. Morris’ al-
gorithm achieves its efficiency by carefully restricting
its edge-generation activity. The rest of this section
describes the theory behind Morris’ algorithm.
Let S be an STNU and G its associated graph. The
lengths of all shortest semi-reducible paths in G can
be determined as follows. First, let G
ou
be the graph
consisting of the ordinary and upper-case edges from
G. G
ou
shall be called the OU-graph for G. Since
the edges in G
ou
are drawn from G, any path in G
ou
also appears in G. In addition, since each path in G
ou
contains only ordinary or upper-case edges, it is nec-
essarily semi-reducible. Thus, the paths in G
ou
are
a subset of the semi-reducible paths in G. Further-
more, since the edge-generation rules from Table 1
only generate ordinary or upper-case edges, inserting
any edges generated by these rules into both G
ou
and
G will necessarily preserve the property of the paths
in G
ou
being a subset of the semi-reducible paths in
G. Fig. 4 shows the OU-graph for the sample STNU
from Fig. 2 before (left) and after (right) the insertion
of two newly generated edges.
Next, since the goal is to compute the lengths
of the paths in G
ou
, let G
x
be the graph obtained
by removing the alphabetic labels from all upper-
case edges in G
ou
. G
x
is called the AllMax graph
because it can be obtained from the original STNU
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
66
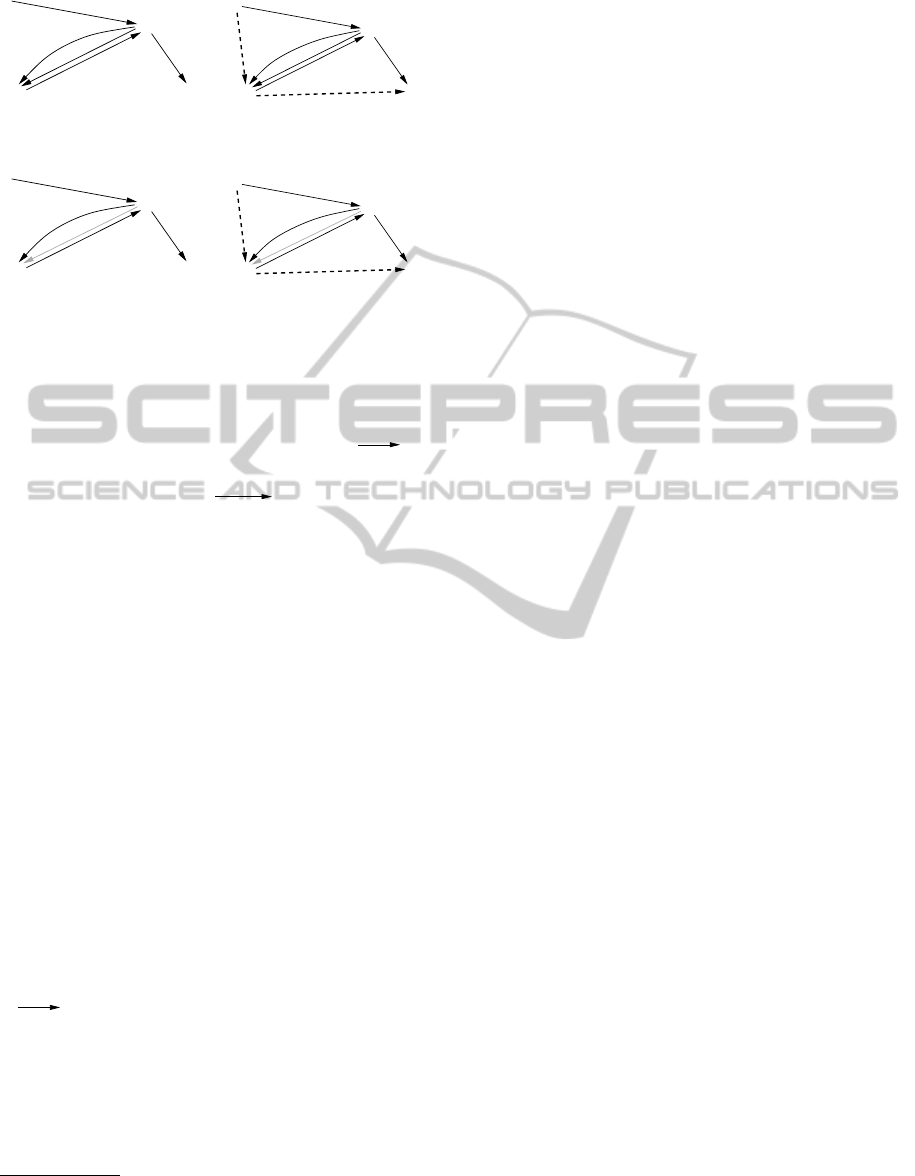
C
A
Y
3
X
−2
10
−5
C : −10
C
A
Y
3
X
−2
10
C : −7
3
−5
C : −10
Figure 4: The OU-graph, G
ou
, for the STNU from Fig. 2
before (left) and after (right) adding newly generated edges.
C
A
Y
3
X
−2
10
−10
−5
C
A
Y
3
X
−2
10
3
−10
−7
−5
Figure 5: The AllMax graph, G
x
, for the STNU from Fig. 2
before (left) and after (right) adding newly generated edges.
by forcing each contingent link to take on its maxi-
mum value (Morris and Muscettola, 2005). The All-
Max graph for the STNU from Fig. 2 is shown in
Fig. 5. In the figure, the ordinary edge, C
−5
A,
is drawn in light gray because it represents a weaker
constraint than the edge, C
−10
A, and thus can be
ignored. Note that if the edge-generation rules pro-
duce an upper-case edge (e.g., the UC edge from Y to
A in Fig. 4), then that edge is stripped of its alphabetic
label before being added to the AllMax graph, G
x
.
Since the AllMax graph contains only ordinary
edges, it is an STN graph. Its associated distance ma-
trix, D
x
, is called the AllMax matrix. For any X and Y ,
D
x
(X,Y ) equals the length of a shortest path from
X to Y in G
x
. D
x
(X,Y ) also equals the length of a
shortest semi-reducible path from X to Y in the OU-
graph, G
ou
. Because G
ou
may contain only a subset
of the semi-reducible paths from G, D
x
(X,Y ) only
provides an upper bound on the length of the short-
est semi-reducible path from X to Y in G. However,
as newly generated edges are inserted into the ap-
propriate graphs, the upper bounds on shortest semi-
reducible path-lengths provided by D
x
may tighten.
Morris’ DC-checking algorithm focuses on edges
that can be generated using the Lower Case and Cross
Case rules (i.e., the two rules that involve lower-case
edges). For example, suppose e is a lower-case edge,
A
c:x
C, in G. Morris’ algorithm searches through
the space of shortest allowable paths emanating from
C.
3
An allowable path with non-positive length is
called an extension sub-path for e. It is not hard to
show that any extension sub-path for e can be trans-
formed into a single edge, e
0
, using the rules from
Table 1. Then either the Lower Case or Cross Case
3
An allowable path for C is any loopless path P in G
ou
emanating from C such that P has no upper-case edges la-
beled by C and all proper prefixes of P have positive length.
Table 2: Pseudo-code for Morris’ DC-checking algorithm.
Input: G, a graph for an STNU with K contingent links.
Output: True if the corresponding STNU is dynamically
controllable; False otherwise.
-1. Gou := OU-graph for G.
0. Gx := AllMax graph for G.
1. for i = 1, K: (Outer Loop)
2. result := Bellman_Ford_SSSP(Gx).
3. if (result == inconsistent) return False.
4. else generate_potential_function(result).
5. newEdges := {}.
6. for j = 1, K: (Inner Loop)
7. Let C
j
be the j
th
contingent time-point.
8. Traverse shortest allowable paths in G
ou
emanat-
ing from C
j
, searching for extension sub-paths that
generate new edges. Add new edges to newEdges.
9. end for j = 1, K.
10. if newEdges empty, return True.
11. else insert newEdges into Gou and Gx.
12. end for i = 1, K.
13. result := Bellman_Ford_SSSP(Gx).
14. if (result == inconsistent) return False.
15. else return True.
rule can be used to transform e and e
0
into a sin-
gle edge, e
00
. The edge, e
00
, is then inserted into
G
ou
and—after removing any alphabetic label—G
x
.
Morris (2006) provides a detailed analysis showing
that, for an STNU with K contingent links, at most
K rounds of this kind of edge generation is required
to determine whether the original graph, G, contains
any semi-reducible negative loops.
Pseudo-code for Morris’ DC-checking algorithm
is given in Table 2. Its most important features are:
• The outer loop (Lines 1–12) runs at most K times.
• Each outer iteration begins (Line 2) by applying
the Bellman-Ford single-source, shortest-paths
(SSSP) algorithm (Cormen et al., 2009) to the All-
Max graph G
x
. This serves two purposes. First, if
Bellman-Ford determines that the AllMax graph
is inconsistent, then Morris’ algorithm immedi-
ately returns False. However if G
x
is consis-
tent, then the shortest-path information generated
by Bellman-Ford can be used to create a potential
function (Line 4) to transform the lengths of all
edges in G
x
—and hence all edges in G
ou
—to non-
negative values, as in Johnson’s algorithm (Cor-
men et al., 2009).
• During each iteration of the outer loop, the inner
loop (Lines 6–9) runs exactly K times, once per
contingent link.
• The j
th
iteration of the inner loop (Lines 7–8) fo-
cuses on C
j
, the contingent time-point for the j
th
AFasterAlgorithmforCheckingtheDynamicControllabilityofSimpleTemporalNetworkswithUncertainty
67

contingent link. The algorithm uses the potential
function generated in Line 4 to enable a Dijkstra-
like traversal of shortest allowable paths emanat-
ing from C
j
in the graph G
ou
.
• New edges generated by K iterations of the inner
loop are accumulated in a set, newEdges (Line 8).
If, after the completion of the inner loop, it is
discovered that no new edges have been gener-
ated, then the algorithm immediately returns True
(Line 10). On the other hand, if some new edges
were generated by the inner loop, then they are in-
serted into the graphs (Line 11) in preparation for
the running of Bellman-Ford at the beginning of
the next iteration of the outer loop (Line 2).
• If, after completing K iterations of the outer loop,
the AllMax graph remains consistent (Lines 14–
15), then the network must be DC.
4
The complexity of Morris’ algorithm is dominated by
the O(N
3
)-time complexity of the Bellman-Ford algo-
rithm (Line 2), as well as the Dijkstra-like traversals
of shortest allowable paths (Line 8). Since Bellman-
Ford is run a maximum of K times, and O(K) = O(N),
the overall complexity due to the use of Bellman-Ford
is O(N
4
). Each Dijkstra-like traversal of shortest al-
lowable paths (Line 8) is O(N
2
) in the worst case.
Since these traversals are run a maximum of K
2
times,
the overall contribution is again O(N
4
).
3 SPEEDING UP DC CHECKING
As discussed above, Morris’ algorithm uses the
Bellman-Ford algorithm to compute a potential func-
tion at the beginning of each iteration of the outer
loop (Lines 2–4). This same potential function is then
used for all K iterations of the inner loop (Lines 6–
9). For this reason, any new edges discovered during
the K iterations of the inner loop cannot be inserted
into G
ou
or G
x
until preparing for the next iteration
of the outer loop (Line 11). To see this, consider that
the Dijkstra-like traversal of shortest allowable paths
(Line 8) depends on all edge-lengths having been con-
verted into non-negative values by the potential func-
tion. Incorporating new edges into this traversal with-
out recomputing the potential function could intro-
duce negative-length edges, violating the conditions
4
This conclusion is justified by Morris’ theorem that an
STNU contains a semi-reducible negative loop if and only
if it contains a breach-free semi-reducible negative loop in
which the extension sub-paths are nested to a depth of at
most K (Morris, 2006). However, the details of that theorem
are beyond the scope of this paper.
of a Dijkstra-like traversal. A second important con-
sequence of delaying the integration of new edges un-
til the next outer iteration, is that the order in which
the contingent links are processed by the inner loop
cannot make any difference to Morris’ algorithm.
The new DC-checking algorithm presented in this
paper uses two inter-related techniques to speed up
the process of DC checking. First, it uses a novel tech-
nique called rotating Dijkstra that permits the new
edges generated by one iteration of the inner loop to
be immediately inserted into the graphs for use during
the next iteration of the inner loop. Second, because
each iteration of the inner loop can use all edges gen-
erated by any prior iteration, the new algorithm uses
a heuristic function, H, to choose a “good” order in
which to visit the contingent links processed by the
inner loop. The heuristic is inspired by the graphical
structure of so-called magic loops analysed in prior
work (Hunsberger, 2013b). In some networks, these
two changes work together to produce an order-of-
magnitude speed-up in DC checking.
Recalling Johnson’s Algorithm. Johnson’s algo-
rithm (Cormen et al., 2009) is an all-pairs, shortest-
paths algorithm that can be used on graphs whose
edges have any numerical lengths: positive, negative
or zero. It begins by using the Bellman-Ford single-
source, shortest-paths algorithm to generate a poten-
tial function, h. In particular, for any node X , h(X)
is defined to be the length of the shortest path from
some source node S to X . Johnson’s algorithm then
uses that potential function to convert edge lengths
to non-negative values, as follows. For any edge,
U
δ
V , the converted length is h(U ) + δ − h(V ).
This is guaranteed to be non-negative since the path
from S to V via U cannot be shorter than the short-
est path from S to V . Then, for each time-point X in
the graph, Johnson’s algorithm runs Dijkstra’s single-
source, shortest-paths algorithm on the re-weighted
edges using X as the source. This works because
shortest paths in the re-weighted graph correspond to
shortest paths in the original graph. In particular, for
any X and Y , the length of the shortest path from X
to Y in the original graph is h(Y ) + D(X,Y ) − h(X),
where D(X ,Y ) is the length of the shortest path from
X to Y in the re-weighted graph.
Rotating Dijkstra. The rotating Dijkstra technique
is based on several observations.
First, just as single-source, shortest-paths infor-
mation can be used to generate a potential function
to support the conversion of edge-lengths to non-
negative values, so too can single-sink, shortest-paths
information be used in this way (Hunsberger, 2013a).
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
68

For example, suppose that S
0
is a given sink node, and
that for each node X , the length of the shortest path
from X to S
0
is available as h
0
(X). Then the conver-
sion of edge lengths to non-negative values can be ac-
complished as follows. For any edge U
δ
V , the
converted length is δ + h
0
(V ) − h
0
(U). Furthermore,
whether the re-weighting of edges is done using a
source-based or sink-based potential function, Dijk-
stra’s algorithm can be run on the re-weighted graph
to find either single-source or single-sink shortest-
paths information. This paper refers to the different
combinations as source-Dijkstra/sink-potential, sink-
Dijkstra/sink-potential, and so on.
Second, when a contingent link, (A, x, y,C), is be-
ing processed during one iteration of the inner loop
of Morris’ algorithm, any new edge generated dur-
ing that iteration must have that link’s activation time-
point, A, as its source.
5
However, adding edges whose
source time-point is A cannot cause changes to the
lengths of shortest paths terminating in A.
6
Thus,
adding new edges whose source is A cannot cause any
changes to entries of the form, D
x
(T, A), for any time-
point T . As a result, if the potential function used to
re-weight the edges for this Dijkstra-like traversal is a
sink-based potential function with A as its sink, then
adding new edges generated by that traversal cannot
cause any changes to that potential function. Thus,
that same potential function can be used along with
Dijkstra’s single-sink, shortest-paths algorithm to re-
compute the values, D
x
(T, A
0
), for any time-point T ,
in preparation for the next iteration of the inner loop,
where A
0
is the activation time-point for the next con-
tingent link to be processed.
Given these observations, the rotating Dijkstra
technique takes the following steps to support the
Dijkstra-like traversal of shortest allowable paths em-
anating from the contingent time-point C associated
with the contingent link (A, x, y,C).
(1) Given: All entries, D
x
(T, A), for all time-points
T . This collection of entries provides a sink-based
potential function, h
A
, where A is the sink.
(2) Use h
A
to convert all edge-lengths in G
ou
to
5
This follows immediately from how new edges are gen-
erated (Morris, 2006). In particular, each new edge is gener-
ated by reducing the path consisting of the lower-case edge,
A
c:x
C, and some extension sub-path into a single new
edge. Since such a reduction preserves the endpoints of the
path, the generated edge must have A as its source.
6
This observation follows from the fact that if X and
Z are distinct time-points in an STN, and P is a short-
est path from X to Z, then there exists a shortest path
from X to Z that does not include any edges of the form,
Z
δ
Y (Hunsberger, 2013a).
C
3
A
3
A
2
C
2
4
X
3
X
2
A
1
C
1
X
1
E
2
E
3
E
1
c
1
: 1
e
3
e
2
−2
−3
3
−2
0
−3
c
2
: 1
c
3
: 1
e
1
−8
Figure 6: A path with nested extension sub-paths
non-negative values in preparation for a source-
Dijkstra traversal of shortest allowable paths em-
anating from C, as in Morris’ algorithm (Line 8).
(3) Since any new edge generated by this traversal
must have A as its source, the edges generated
by this traversal cannot cause changes to the sink-
based potential function, h
A
. Thus, the same func-
tion, h
A
, can be used to support a sink-Dijkstra
computation of all entries of the form D
x
(T, A
0
),
for any T , where A
0
is the activation time-point
for the next contingent link to be processed. This
computation is abbreviated as sink-Dijkstra/sink-
potential(A
0
, A), since A
0
is the sink for Dijkstra,
and A is the sink for the potential function.
For the very first iteration of the inner loop, the en-
tries, D
x
(T, A), needed in Step 1 are provided by an
initial run of Johnson’s algorithm. For every subse-
quent iteration, the information needed in Step 1 is
obtained from Step 3 of the preceding iteration.
Choosing an Order for the Contingent Links.
Because the rotating Dijkstra technique enables newly
generated edges to be inserted into the network imme-
diately, rather than waiting for the next iteration of the
outer loop, edges generated by one iteration of the in-
ner loop can be used by the very next iteration. Thus,
subsequent iterations of the inner loop may generate
new edges sooner than they would in Morris’ algo-
rithm, which can significantly improve performance.
Consider the path shown in Fig. 6. The innermost
sub-path, from A
1
to X
1
, reduces to (i.e., can be trans-
formed into) a new edge, E
1
, from A
1
to X
1
. In turn,
that enables the next innermost sub-path, from A
2
to
X
2
, to be reduced to a new edge, E
2
, from A
2
to X
2
.
Finally, that then enables the outermost path, from A
3
to X
3
, to be reduced to a single new edge, E
3
, from A
3
to X
3
. Thus, in this example, if the contingent links
are processed in the order, C
1
,C
2
,C
3
, then all three
edges, E
1
, E
2
and E
3
, will be generated in one itera-
tion of the outer loop—involving three iterations of
AFasterAlgorithmforCheckingtheDynamicControllabilityofSimpleTemporalNetworkswithUncertainty
69

the inner loop. However, if the contingent links are
processed in the opposite order, then three iterations
of the outer loop—involving nine iterations of the in-
ner loop—will be required to generate E
1
, E
2
and E
3
.
To see this, notice that if C
3
is processed first, then
the edges E
1
and E
2
will not have been generated yet.
And, since allowable paths do not include lower-case
edges, the initial search through allowable paths em-
anating from C
3
will not yield any new edges. Sim-
ilarly, the initial search through allowable paths em-
anating from C
2
will not yield any new edges. Only
the processing of C
1
will yield a new edge—namely,
E
1
—during the first iteration of the outer loop. Dur-
ing the second iteration of the outer loop, the process-
ing of C
2
will yield the edge E
2
. Finally, during the
third iteration of the outer loop, the processing of C
3
will yield the edge E
3
. Crucially, since Morris’ algo-
rithm does not insert new edges until the beginning of
the next iteration of the outer loop, Morris’ algorithm
would exhibit the same behavior for this path.
⇒ In general, Morris’ algorithm requires d itera-
tions of the outer loop to generate new edges aris-
ing from semi-reducible paths in which extension
sub-paths are nested to a depth d.
Nesting Order. Prior work (Hunsberger, 2013b)
has defined a nesting order for semi-reducible paths
as follows. Suppose e
1
, e
2
, . . . , e
n
are the lower-case
edges that appear in a semi-reducible path P . Then
that ordering of those edges constitutes a nesting or-
der for P if i < j implies that no extension sub-path
for e
j
is nested within an extension sub-path for e
i
in
P . For example, the path shown in Fig. 6 has a nest-
ing order e
1
, e
2
, e
3
. The relevance of a nesting order
to DC checking is revealed by the following:
⇒ If a semi-reducible path P has extension sub-
paths nested to a depth d, with a nesting order,
e
1
, e
2
, . . . , e
d
, and the lower-case edges (i.e., the
contingent links) are processed in that order using
the rotating Dijkstra technique, then only one iter-
ation of the outer loop will be necessary to gener-
ate all edges derivable from P .
For the purposes of this paper, it is not necessary
to prove this result—although it follows quite eas-
ily from the definitions involved—because it is not
claimed that for any STNU graph there is a single
nesting order that applies to all semi-reducible paths
in that graph. However, it does suggest that it might
be worthwhile to spend some modest computational
effort to find a “good” order in which to process the
contingent links in the inner loop of the algorithm.
Toward that end, suppose that e
1
and e
2
are lower-
case edges corresponding to the contingent links,
(A
1
, x
1
, y
1
,C
1
) and (A
2
, x
2
, y
2
,C
2
). If e
1
is nested in-
side e
2
in a semi-reducible path, P (e.g., as in Fig. 6),
then there must exist a path from C
2
to A
1
consist-
ing of ordinary or upper-case edges whose length is
positive. (This is part of the definition of an allow-
able path.) Now, allowable paths for the lower-case
edge e
2
cannot include any upper-case edges labeled
by C
2
7
, whereas the OU-graph invariably includes at
least one upper-case edge labeled by C
2
. Thus, the
corresponding AllMax matrix entry, D
x
(C
2
, A
1
), is not
a perfect substitute for the length of the shortest al-
lowable path from C
2
to A
1
. Instead, D
x
(C
2
, A
1
) is a
lower bound on that length. Nonetheless, the heuristic
presented below uses it as an imperfect substitute.
The Heuristic, H. Let G be the graph for an STNU
with K contingent links, and G
x
the corresponding
AllMax graph. Run Johnson’s algorithm on G
x
to gen-
erate the AllMax matrix D
x
. For each i, let Q(i) be the
number of entries of the form D
x
(C
i
, A
j
) that are non-
positive. Let H(G) be a permutation, σ
1
, σ
2
, . . . , σ
K
,
such that r < s implies Q(σ
r
) ≤ Q(σ
s
). In other
words, H(G) is obtained by sorting the numbers
1, 2, . . . , K according to the corresponding Q values.
The Algorithm. Pseudo-code for the new DC-
checking algorithm is given in Table 3. The algorithm
first constructs the OU-graph, G
ou
, and the AllMax
graph, G
x
(Lines -1 and 0). It then uses Johnson’s al-
gorithm to compute the AllMax matrix, D
x
(Line 1).
As discussed above, D
x
is used during the computa-
tion of the heuristic function, H (Line 2), which de-
termines the processing order for the contingent links.
These D
x
entries also provide the potential function in
Line 9 during the very first iteration of the inner loop.
GlobalIters, initially 0 (Line 3), counts the total
number of iterations of the inner loop. If this counter
ever reaches K
2
, the algorithm terminates, returning
True (Line 13).
8
LocalIters, initially 0 (Line 4),
counts the number of consecutive iterations of the in-
ner loop since the last time a new edge was generated.
If this counter ever reaches K, then the algorithm ter-
minates, returning True (Line 16).
9
In the new algorithm, the inner loop (Lines 6–
19) cycles through the contingent links in the order
given by the heuristic until a termination condition is
reached. Since potential functions are re-computed
7
Morris calls such edges breaches. The allowable paths
traversed by his algorithm are breach-free.
8
This termination condition is analogous to Morris’ al-
gorithm terminating after K iterations of the outer loop.
9
This termination condition is analogous to Morris’ al-
gorithm terminating whenever any iteration of the outer
loop fails to generate a new edge.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
70

Table 3: Pseudo-code for the new DC-checking algorithm.
Input: G, a graph for an STNU with K contingent links.
Output: True if the corresponding STNU is dynamically
controllable; False otherwise.
-1. Gou := OU-graph for G;
0. Gx := AllMax graph for G;
1. Dx := Johnson(Gx);
2. Order := Heuristic(Dx);
3. GlobalIters := 0;
4. LocalIters := 0;
5. for i = 1, K: (Outer Loop)
6. for j = 1, K: (Inner Loop)
7. newEdges := {};
8. Let (A
j
, x
j
, y
j
,C
j
) be the j
th
contingent link
according to Order.
9. Use the values, D
x
(T, A
j
), as a sink-based poten-
tial function, h
A
j
, to transform the edge-lengths in
Gx and Gou to non-negative values.
10. Traverse shortest allowable paths in G
ou
emanat-
ing from C
j
, searching for extension sub-paths that
generate new edges. Add such edges to newEdges.
11. for each edge A
j
δ
X in newEdges:
if (δ < −D
x
(X, A
j
)) return False;
12. GlobalIters++;
13. if (GlobalIters ≥ K
2
) return True;
14. elseif newEdges empty:
15. LocalIters++;
16. if (LocalIters ≥ K) return True;
17. else LocalIters := 0;
18. run sinkDijkSinkPot(A’,Aj), where A
0
is the
activation time-point for the next contingent link.
19. end for j = 1, K.
20. end for i = 1, K.
21. return True.
after each inner iteration (Line 18), the outer loop is
provided only for counting purposes.
One iteration of the inner loop spans Lines 7–18.
(A
j
, x
j
, y
j
,C
j
) is the contingent link to be processed,
as determined by Order. For the very first iteration
of the inner loop, the values, D
x
(X, A
j
), that con-
stitute a sink-based potential function (Line 9), are
provided by Johnson’s algorithm (Line 1); for every
other iteration of the inner loop, these values are pro-
vided by the sink-Dijkstra/sink-potential computation
from Line 18 of the previous iteration. This potential
function is then used in Line 10 to support a source-
Dijkstra traversal of shortest allowable paths emanat-
ing from C
j
. Because the values, D
x
(X, A
j
), are avail-
able for all time-points X, any new edge from A
j
to
some X can be immediately checked for consistency
(Line 11). If all new edges are judged to be consistent,
then the algorithm increments the global counter and
checks the two termination conditions (Lines 13 and
16). If no termination condition is reached yet, then a
sink-Dijkstra/sink-potential computation is run (Line
18), to compute all entries of the form, D
x
(X, A
0
),
where A
0
is the activation time-point for the contin-
gent link to be processed during the next iteration of
the inner loop. These values will form the potential
function in Line 9 during the next iteration.
4 EMPIRICAL EVALUATION
The new DC-checking algorithm was evaluated by
comparing it against Morris’ DC-checking algorithm.
Both algorithms were implemented in Allegro Com-
mon Lisp using the same data structures and support-
ing functions.
Testing on Magic Loops. The purpose of the first
test was to verify that on so-called magic loops,
which represent one kind of worst-case scenario for
DC-checking algorithms (Hunsberger, 2013b), Mor-
ris’ algorithm requires K iterations of the outer loop,
whereas the new algorithm requires only one itera-
tion of the outer loop. For each K ∈ {1, 2, . . . , 13},
an STNU containing a magic loop involving K con-
tingent links was generated using the parameter val-
ues given in prior work (Hunsberger, 2013b). For
each network, the heuristic, H, correctly generated
the unique nesting order for the contingent links in
that network’s magic loop. In terms of iterations of
the inner-loop, Morris’ algorithm required K
2
itera-
tions to process a magic loop of order K, whereas the
new algorithm requires only K iterations—an order-
of-magnitude improvement.
Testing on Randomly Generated Networks. The
next set of tests compared the performance of the
two DC-checking algorithms on a variety of randomly
generated, dynamically controllable STNUs. Since
both algorithms perform extremely well on networks
having little nesting of extension sub-paths, the net-
works in these tests were intentionally created to have
significant levels of such nesting. The goal of the tests
was to determine whether the new algorithm would be
able to take advantage of its heuristic ordering func-
tion and the rotating Dijkstra technique to speed up
DC checking in the presence of significant levels of
nesting of extension sub-paths.
Each network was created by, first, seeding it
with several semi-reducible paths with different lev-
els of nesting, and then randomly inserting edges
among different pairs of time-points. For example,
in the test, test(40)(24-12-6-3)(500), each net-
work was initially seeded with semi-reducible paths
AFasterAlgorithmforCheckingtheDynamicControllabilityofSimpleTemporalNetworkswithUncertainty
71

of depths 24, 12, 6 and 3, involving a total of 45 con-
tingent links and 139 time-points, and then up to 500
edges were inserted among random pairs of time-
points.
10
A total of 40 such networks were gener-
ated for this test. Each network was given as in-
put to both algorithms. For each network/algorithm
combination, the run-time (in milliseconds) and the
number of iterations of the inner loop were recorded.
In addition, the ratio of run-times,
MorrisTime
NewAlgTime
, and
the ratio of iterations-used,
MorrisNumIters
NewAlgNumIters
, were com-
puted. Although the run-times of each algorithm var-
ied markedly across different networks, these ratios
were quite stable. For example, in the test described
above, the average run-time for Morris’ algorithm
was 330 ± 1308 msec and the average run-time for
the new algorithm was 228 ± 352 msec, but the aver-
age ratio of run-times was 1.47 ± 0.03, a very sig-
nificant result that indicates that Morris’ algorithm
took almost fifty percent longer to compute its an-
swer. The average numbers of iterations of the in-
ner loops used by each algorithm were similarly quite
varied, but the ratio of these numbers was very stable:
2.12±0.05, a very significant result that indicates that
Morris’ algorithm required over twice as many itera-
tions of the inner loop to compute its answer.
11
In
view of the above, the results for each test given be-
low provide the much more stable ratios of run-times
and numbers-of-iterations, instead of the much more
volatile raw numbers.
The tests in this set are notated,
test(Trials)(D1-D2-D3-D4)(Edges), where Trials
specifies the number of networks generated, D1,
D2, D3 and D4 specify the depths of nesting of the
semi-reducible paths used to seed the network, and
Edges specifies an upper bound on the number of
additional edges that were randomly generated for
the network. For each test, the following charac-
teristics of the randomly generated networks are
reported: number of time-points (N), number of
contingent links (K), average number of edges (E),
average maximum depth (D) of nesting of extension
sub-paths in the network. Finally, the run-time (RT)
and number-of-iterations (It) ratios are also reported.
The test results are shown in Table 4. The results
clearly demonstrate that the new algorithm performs
significantly better than Morris’ algorithm. Further-
10
To ensure the dynamic controllability of the resulting
generated network, some of the randomly generated edges
were discarded. On average, each network in this test had
446 ± 78 edges.
11
The timing ratio and the iterations ratio are different be-
cause Morris’ algorithm runs Bellman Ford once per outer
iteration, whereas the new algorithm runs an extra sink-
Dijkstra/sink-potential routine once per inner iteration.
Table 4: DC checking test results.
Test N K E D RT ratio It ratio
T0 58 18 295 ± 146 6.7 ± 0.6 1.29 ± .07 1.82 ± .04
T1 139 45 446 ± 78 11.5 ± 1.2 1.47 ± .03 2.12 ± .05
T2 139 45 321 ± 27 12.8 ± 1.9 1.58 ± .03 2.33 ± .06
T3 184 60 713 ± 219 14.7 ± 2.0 1.63 ± .04 2.36 ± .08
T4 229 75 569 ± 115 17.6 ± 3.5 1.80 ± .04 2.51 ± .07
T0 = test(40)(8-4-4-2)(400)
T1 = test(40)(24-12-6-3)(500)
T2 = test(100)(24-12-6-3)(300)
T3 = test(40)(32-16-8-4)(900)
T4 = test(40)(40-20-10-5)(600)
more, as the nesting depth, D, of extension sub-paths
increases, the ratio of improvement increases. For ex-
ample, the run-time ratio (RT ratio) increased from
1.29 to 1.80 as the average nesting depth increased
from 6.7 to 17.6. Stated differently, Morris’ algorithm
took 29 percent longer on average for the networks
having an average nesting depth of 6.7, but took 80
percent longer on average for the networks having an
average nesting depth of 17.6.
5 CONCLUSIONS
This paper presented a new DC-checking algorithm
for STNUs that is demonstrated to outperform, on av-
erage, the state-of-the-art DC-checking algorithm due
to Morris, especially for networks with a substantial
amount of nesting of extension sub-paths. The new
algorithm combines two new techniques: the rotating
Dijkstra technique that enables newly generated edges
to be immediately incorporated into the network, and
a heuristic function that determines a “good” order in
which to process the contingent links.
Future work will carry out a more exhaustive em-
pirical evaluation, with an eye toward improving the
ordering heuristic. Further work will explore the po-
tential of using these kinds of techniques to provide a
lower bound on the worst-case complexity of the DC-
checking problem.
REFERENCES
Chien, S., Sherwood, R., Rabideau, G., Zetocha, P., Wain-
wright, R., Klupar, P., Gaasbeck, J. V., Castano, R.,
Davies, A., Burl, M., Knight, R., Stough, T., and Ro-
den, J. (2002). The techsat-21 autonomous space sci-
ence agent. In The First International Joint Confer-
ence on Autonomous Agents and Multiagent Systems
(AAMAS-2002), pages 570–577. ACM Press.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C.
(2009). Introduction to Algorithms. MIT Press.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
72

Dechter, R., Meiri, I., and Pearl, J. (1991). Temporal con-
straint networks. Artificial Intelligence, 49:61–95.
Hunsberger, L. (2013a). A faster execution algorithm for
dynamically controllable STNUs. In Proceedings of
the 20th Symposium on Temporal Representation and
Reasoning (TIME-2013).
Hunsberger, L. (2013b). Magic loops in simple temporal
networks with uncertainty. In Proceedings of the Fifth
International Conference on Agents and Artificial In-
telligence (ICAART-2013).
Hunsberger, L., Posenato, R., and Combi, C. (2012). The
dynamic controllability of conditional stns with un-
certainty. In Proceedings of the PlanEx Workshop at
ICAPS-2012, pages 121–128.
Morris, P. (2006). A structural characterization of temporal
dynamic controllability. In Principles and Practice of
Constraint Programming (CP 2006), volume 4204 of
Lecture Notes in Computer Science, pages 375–389.
Springer.
Morris, P., Muscettola, N., and Vidal, T. (2001). Dynamic
control of plans with temporal uncertainty. In Nebel,
B., editor, 17th International Joint Conference on Ar-
tificial Intelligence (IJCAI-01), pages 494–499. Mor-
gan Kaufmann.
Morris, P. H. and Muscettola, N. (2005). Temporal dynamic
controllability revisited. In Veloso, M. M. and Kamb-
hampati, S., editors, The 20th National Conference on
Artificial Intelligence (AAAI-2005), pages 1193–1198.
MIT Press.
AFasterAlgorithmforCheckingtheDynamicControllabilityofSimpleTemporalNetworkswithUncertainty
73
