
Investment Lags
A Numerical Approach
M. Al-Foraih, P. Johnson and P. Duck
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, U.K.
Keywords:
Real Option, Stochastic Models, Time-Varying Demand, Investment Lag.
Abstract:
In this paper we use a mixture of numerical methods including finite difference and body fitted co-ordinates
to form a robust stable numerical scheme to solve the investment lag model presented in the paper by Bar-Ilan
and Strange (1996). This allows us to apply our methodology to models with different stochastic processes
that does not have analytic solutions.
1 INTRODUCTION
Most investment projects take a long time to become
operational so there are often periods where a firm
will incur losses before the project starts generating
income. Such a period might be referred to as the
“construction lag”, “time to build ” or “Investment
Lag” (Costeniuc et al., 2008). These investment lags
can be quite lengthy which can result in a serious cost
for the investor, an example of which is described by
(MacRae, 1989) where it could take up to 10 years
to see the positive income when investing in a power
generating plant – similar situations can be found in
investment projects on natural resources. For exam-
ple, when an oil company buys a license from a gov-
ernment, it takes time to search fields and estimate
the fields’ reserve quantity before the beginning of oil
production. Thus, when evaluating a project such as
this the “lag” should be taken into consideration. If
the sale price of a firm’s product is modelled by a
stochastic process, then the lag brings added risk to
the project since the price may rise or fall during this
lag, resulting in a negative cash flow. This situation
and its effect on an investment has been studied by
(Gauthier and Morellec, 2000) and they implied that
it a has significant consequences on investment deci-
sions.
The use of option theory to value and assess in-
vestment decisions has a long history going back to
(Myers, 1977), but it was (Brennan and Schwartz,
1985) that first allowed the project to be mothballed
rather than abandoned so that it could be reopened at a
later date. They showed that if there was a fixed cost
to move between the states, the decision to start the
project would happen at a price higher than the deci-
sion to mothball. Following on from this, (Bar-Ilan
and Strange, 1996) applied investment lags on irre-
versible investments and they found that a lag can re-
duce the effects of uncertainty in an investment, since
the investor has more time to act on an unexpected
fall in the price or changes in the investment. In order
to generate the results for their model, they present an
analytic technique,(see Brekke and Øksendal, 1994,
for more details. The method as described by (Bar-
Ilan and Strange, 1996) is flawed in that it relies on the
particular form of the process, so they can only solve
the problem with a simple geometric Brownian mo-
tion. The contribution of this paper is to apply a more
generic numerical approach which can be extended to
many classes of stochastic processes. We present a
robust numerical technique for solving generic prob-
lems of this type.
2 MODEL FRAMEWORK
We follow the general framework as laid down by
(Bar-Ilan and Strange, 1996) in valuing a firm that
can pay (on delivery) k ≥ 0 units to exercise an ir-
reversible option to produce and sell 1 unit of product
per unit time forever. The marginal cost of production
is ω per unit, and both the future revenues and costs
are discounted at the rate of ρ. The project can later be
abandoned at a cost of l ≥0. The price of the product
P
t
follows a standard geometric Brownian motion
dP
P
= µdt + σdz. (1)
282
Al-Foraih M., Johnson P. and Duck P..
Investment Lags - A Numerical Approach.
DOI: 10.5220/0004920702820287
In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 282-287
ISBN: 978-989-758-017-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

where
• µ is the rate of return of the product P
t
,
• σ is the volatility of the product price P
t
,
• dz is the increment of the standard Wiener pro-
cess.
When the investment starts, in many cases, it takes
time from the decision to invest until the time the
project begins to generate revenue. For example, if
a firm wishes to build an oil refinery it will make that
decision depending on today’s oil price but it usually
takes around 6 −7 years to start producing oil (Sen-
ate, 2002). We shall denote h ≥0 to be the investment
lag in our model.
As a result the firm at any one time may be in three
different states. The states are characterised as
• V
0
(P) Inactive firm.
In this stage there is no money invested and
no revenue.
• V
2
(P,t) the firm in the process of construction
where t is the clock that starts after the decision
is made (0 ≤ t ≤ h).
In this stage the firm has made the decision
to invest and is waiting until time h when the firm
will pay k and start production.
• V
1
(P) Active firm and generating revenue.
In this state we have invested the amount k
and it is working and generating the amount of P
for each unit produced.
Our goal is to find at what price of the product should
we invest and for what price should we leave the
project. We shall denote P
H
as the price at which it
is high enough to start construction at a cost of ke
−ρh
(discounted value of the payment at time t = 0), and
P
L
as the price of product which is low enough to
abandon the project for cost of l.
2.1 Calculating the Firm’s Value at
Different Situations
Suppose it is not optimal to invest at an infinitesimal
period of dt, then
V
0
(P
t
) = e
−ρdt
E
t
[V
0
(P
t+dt
)], (2)
where P
t
is the price at time t. Using Ito’s Lemma we
can write
σ
2
2
P
2
V
′′
0
(P) + µPV
′
0
(P) −ρV
0
(P) = 0. (3)
The boundary condition for P = 0 is simply
lim
P→0
V
0
(P) = 0, (4)
and given that we optimally decide to invest the fol-
lowing must hold
V
0
(P
H
) = V
2
(P
H
) −ke
−ρh
(5)
V
′
0
(P
H
) = V
′
2
(P
H
). (6)
General solutions to the ODE in (3) can be found
of the form
V
0
(P) = BP
β
(7)
where B is a constant and β is the positive solution of
the characteristic equation of
σ
2
2
ξ(ξ−1) + µξ−ρ = 0. (8)
For V
1
(P), if we assume it is optimal to sell prod-
ucts over the next small period in time we have
V
1
(P
t
) = e
−ρdt
E
t
[V
1
(P
t+dt
)]
+ E
t
Z
t+dt
t
(P
t
−ω)e
−ρ(τ−t)
dτ
,
where the extra term here is the total amount of profit
from selling at the rate one product per unit time. We
calculate the value of the active firm in the same man-
ner as we did in the inactive case to arrive at
σ
2
2
P
2
V
′′
1
(P) + µPV
′
1
(P) −ρV
1
(P) = ω −P. (9)
The boundary condition as P → ∞ takes the form
lim
P→∞
V
1
(P) = lim
P→∞
P
ρ−µ
−
ω
ρ
. (10)
Therefore, solutions of equation (9) can be written
V
1
(P) = AP
α
+
P
ρ−µ
−
w
ρ
, (11)
where A is yet to be determined and α is the nega-
tive solution of equation (8). Since we can optimally
decide to shut down operations we also have
V
1
(P
L
) = V
0
(P
L
) −l (12)
V
′
1
(P
L
) = V
′
0
(P
L
). (13)
These form the solution of the investment and
disinvestment problem in Pindyck and Dixit (1996),
where the time to build is not considered. For the in-
vestment lag problem, we must now consider the extra
state of the firm V
2
(P,t) during the lag. Giving that we
are waiting for production to start we can write
V
2
(P
t
,t) = e
−ρdt
E
t
[V
2
(P
t+dt
,t + dt)], (14)
and following standard procedure we obtain
∂V
2
∂t
+
1
2
σ
2
P
2
∂
2
V
2
∂P
2
(15)
+ µP
∂V
2
∂P
−ρV
2
= 0
InvestmentLags-ANumericalApproach
283

where the boundary conditions are
lim
P→0
V
2
(P,t) = −le
−ρ(h−t)
, (16)
lim
P→∞
V
2
(P,t) = lim
P→∞
Pe
(ρ−µ)(h−t)
ρ−µ
−
ωe
−ρ(h−t)
ρ
, (17)
and
lim
t→h
V
2
(P,t) =
AP
α
+
P
ρ−µ
−
ω
ρ
if P ≥P
L
BP
β
−l if P < P
L
.
These equations describe the three states of the firm,
which all need to be solved to determine P
L
and P
H
.
3 NUMERICAL APPROACH
Although this problem has been solved in (Bar-Ilan
and Strange, 1996) and later again by (Sødal, 2006),
in this paper we present a new methodology which
gives more flexibility to the practitioner. The idea is to
solve the problem using finite differences with body-
fitted co-ordinates to quickly solve for P
H
and P
L
. To
simplify the algebra in the method we first apply a log
transformation to the ODEs (3) and (9) and the PDE
(15).
3.1 Derivation
To solve the problem we define two grids of x and y
each of which have m+ 1 points. We apply log trans-
forms to the equations involving V
1
and V
2
by setting
P = P
L
e
y
=⇒ y = ln
P
P
L
, (18)
The grid itself is generated from
∆y =
y
min
−y
max
m
. (19)
using the parameters
y
min
= 0 and y
max
= 10σ
√
h. (20)
Likewise, for equation involving V
0
we apply a log
transform
P = P
H
e
x
=⇒ x = ln
P
P
H
. (21)
The grid becomes
∆x =
x
min
−x
max
m
. (22)
such that
x
min
= −10σ
√
h and x
max
= 0. (23)
First we can apply the log transform (18) to the
equation of the active firm value (9) to get
σ
2
2
∂
2
V
1
∂y
2
+ (µ−
σ
2
2
)
∂V
1
∂y
−ρV
1
= ω−P
L
e
y
. (24)
Using the notation
v
i
1
= V
1
(P = P
L
e
i∆y
) = V
1
(e
y
i
) (25)
we apply standard finite differencing and a Newton
linearisation with
v
i,k+1
1
≃ v
i,k
1
+ δv
i
1
and P
k+1
L
≃ P
k
L
+ δP
L
(26)
where k is the number of iterations. The resulting
scheme is given by
σ
2
2(∆y)
2
−
2µ−σ
2
4∆y
δv
i−1
1
+
−
σ
2
2(∆y)
2
−ρ
δv
i
1
(27)
+
σ
2
2∆y
+
2µ−σ
2
4∆y
δv
i+1
1
+ e
y
i
δP
L
= F (P) (28)
where
F (P) = −
1
2
σ
2
v
i−1
1
−2v
i
1
+ v
i+1
1
2(∆y)
2
(29)
−(µ−
1
2
σ
2
)
v
i+1
1
−v
i−1
1
2∆y
+ ρv
i
1
−P
i
L
e
y
i
+ ω.
Now for the smooth pasting boundary conditions we
use a one sided difference of the form
V
′
1
(P = P
L
) =
−3(v
0
1
+ δv
0
1
) + 4(v
1
1
+ δv
1
1
) −(v
2
1
+ δv
2
1
)
2∆yP
L
(30)
and to calculateV
′
0
(P
L
) we use central differencing
V
′
0
(P
L
) =
V
0
(P
L
(1+ ∆y)) −V
0
(P
L
(1−∆y))
2∆yP
L
(31)
where the values of V
0
(P
L
(1 + ∆y)) and
V
0
(P
L
(1−∆y)) must be interpolated. For the
contact boundary condition at P = P
L
we expand with
a Taylor series to get
δv
0
1
−V
′
0
(P
L
)δP
L
= V
0
(P
L
) −v
0
1
(32)
Similarly, for the inactive or mothballed firm
V
0
(P) defined in equation(3), we apply a log transfor-
mation on P
H
with standard differencing and a New-
ton linearisation. The result is the same left hand side
as in (28) with δv
i
1
and δP
L
replaced by δv
i
0
and δP
H
,
and the right hand side is now given by
F (P) = −
1
2
σ
2
v
i−1
0
−2v
i
0
+ v
i+1
0
2(∆x)
2
− (33)
(µ−
1
2
σ
2
)
v
i+1
0
−v
i−1
0
2∆x
+ ρv
i
0
.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
284

As before the boundary conditions become
δv
m
0
−V
′
2
(P
H
)δP
H
= V
2
(P
H
) −ke
−ρh
−v
m
0
(34)
and
3δv
m
0
−4δv
m−1
0
+ δv
m−2
0
2∆xP
H
= V
′
2
(P
H
)−
3v
m
0
−4v
m−1
0
+ v
m−2
0
2∆xP
H
(35)
where V
2
(P
H
) here is V
2
(P
H
,t = 0) which must be
calculated from (15).
We can use either quadrature integration (Andri-
copoulos et al., 2003) or finite difference to solve
for V
2
in (15). For any point x of the n points on
V
2
(x,t = 0) we have
V
2
(x,t = 0) = A(x)
Z
∞
−∞
B(x,y)V
2
(y,t = h)dy, (36)
then we calculate the value of V
2
using
A(x) =
1
√
2σ
2
πh
e
−
1
2
kx−
1
8
σ
2
k
2
h−ρh
, (37)
and
B(x,y) = e
−(x−y)
2
/2σ
2
h+1/ky
, (38)
and
k =
2(ρ−d)
σ
2
−1 (39)
where d is the dividends (d = ρ −µ). The reason we
calculate V
2
(y,t = 0) usingV
2
(y,t = h) that is because
we solve the problem backwards in time where
V
2
(y,t = h) =
V
1
(y) if e
y
> 1(P > P
L
)
V
0
(y) −l if e
y
≤ 1(P ≤ P
L
)
.
(40)
Given the fact we have applied a different transforma-
tions on V
0
andV
1
we must interpolateV
0
to get values
in the y grid points using the relation
x = y
i
+ log(
P
H
P
L
). (41)
We may use the asymptotic form of the solution to fill
in the gaps outside the grid, then we write
V
2
(x,t = 0) = A(x)(
Z
y
max
y
min
B(x,y)V
2
(y,t = h)dy+ I
1
+ I
3
)
(42)
where
I
1
= −
Z
y
min
−∞
B(x,y)le
h
dy (43)
and
I
3
=
Z
∞
y
max
B(x,y)(
e
y−(ρ−µ)h
ρ−µ
−
we
−ρh
ρ
)dy (44)
4 Cox-Ingersoll-Ross MODEL
In a novel extension to the problem, we set the pro-
cess followed by the sale price as a Cox-Ingersoll-
Ross (CIR) process. These sort of processes are often
appropriate when modelling commodity prices as the
price tends to a mean value over a long time scale. We
can write the new price process as
dP = κ(Φ−P)dt + σ
√
Pdz (45)
such that
• κ is the speed of reversion
• Φ : is the long term mean level
and σ and P are as defined previously. Now the equa-
tions of V
0
(P), V
1
(P) and V
2
(P) will become
σ
2
2
PV
′′
0
(P) + κ(Φ−P)V
′
0
(P) −ρV
0
(P) = 0, (46)
σ
2
2
PV
′′
1
(P)+κ(Φ−P)V
′
1
(P)−ρV
1
(P) = w−P. (47)
and
∂V
2
∂t
+
P
2
σ
2
∂
2
V
2
∂P
2
(48)
+ κ(Φ−P)
∂V
2
∂P
−ρV
2
= 0.
At P = 0 we solve the degenerate ODE for V
0
κΦV
′
0
−ρV
0
= 0 (49)
and the degenerate PDE for V
2
∂V
2
∂t
+ κΦ
∂V
2
∂P
−ρV
2
= 0 (50)
For large P we set
V
1
∼P
−
ρ
κ
+
P
ρ+ κ
+
κΦ
ρ(ρ+ κ)
−
ω
ρ
, as P → ∞, (51)
and assume a linear solution for V
2
so solve
∂V
2
∂t
+ κΦ
∂V
2
∂P
−ρV
2
= 0. (52)
The terminal condition for V
2
is as before given by
V
2
(P,t = h) =
V
1
(P) if P ≥P
L
V
0
(P) −l if P < P
L
The smooth pasting conditions are the same as
those defined in equations (5), (6) and (12), (13). We
now transform the P-grid with a linear stretch get x
and y grids
P = yP
L
for V
1
(P) = V
1
(yP
L
)
P = xP
H
for V
0
(P) = V
0
(xP
H
). (53)
InvestmentLags-ANumericalApproach
285
0
2
4
6
8
10
12
0 0.2 0.4 0.6 0.8 1
V0
V1
V2
V
P
Figure 1: the Prices of V
0
, V
1
and V
2
with σ
2
= 0.1,ρ =
0.025,µ = 0, ω = 1., l = 0,k = 1, h = 6 years grid size of
1000.
and
x ∈[0, 1]
y ∈[1,y
max
]. (54)
Therefore, equation (47) will be transformed to
1
2
σ
2
yV
′′
1
+ κ(Φ−yP
L
)V
′
1
−ρP
L
V
1
= P
L
(ω−yP
L
)
(55)
and (46) will be transformed to
1
2
σ
2
xV
′′
0
+ κ(Φ−xP
H
)V
′
0
−ρP
H
V
0
= 0. (56)
We can follow the same method using a finite differ-
ence scheme with Newton linearisation. To calcu-
late V
2
, we must now solve the PDE using a Crank-
Nicolson scheme since the kernel does not exist for
this price process.
5 RESULTS
In figure 1, the switch from closed to in-construction
(V
0
→V
2
−ke
−ρh
) happenswhen P
H
= 1.14632 which
is the optimal price to start construction, while at
P
L
= 0.793442 the price is so low that it is not worth
continuing production (V
1
→ V
0
−l). We can notice
in this figure that P
H
is higher than P
L
, which is to
be expected since we should only invest if the price
is higher than the abandon price. Now we compare
our results to those of (Sødal, 2006) in figure 3, and
we find that our method generates values of P
L
and P
H
that are very close to the previous method. To demon-
strate the integrity of our scheme, in figure 2 we plot
the value of P
L
for an increasing number of nodes.
The convergence of the scheme can be shown empiri-
cally to be second order which matches with the finite
difference methods used.
0.059
0.0595
0.06
0.0605
0.061
0.0615
0.062
0.0625
0 500 1000 1500 2000 2500 3000
price
nodes
PL
Figure 2: The convergence of P
L
as we increase the
nodes to calculate P
L
using the numerical method with
ρ = 0.035,µ = 0.5, ω = 2., l = 3,k = 2,h = 4, σ
2
= 0.02.
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
0 0.2 0.4 0.6 0.8 1
Pl Quad
Ph Quad
pl paper
Ph paper
P
σ
2
Figure 3: The values of P
L
of P
H
with µ = 0,ρ = .025,l =
0,k = 1, ω = 1, σ
2
= 0.01 using Algebraic equations vs the
numerical method.
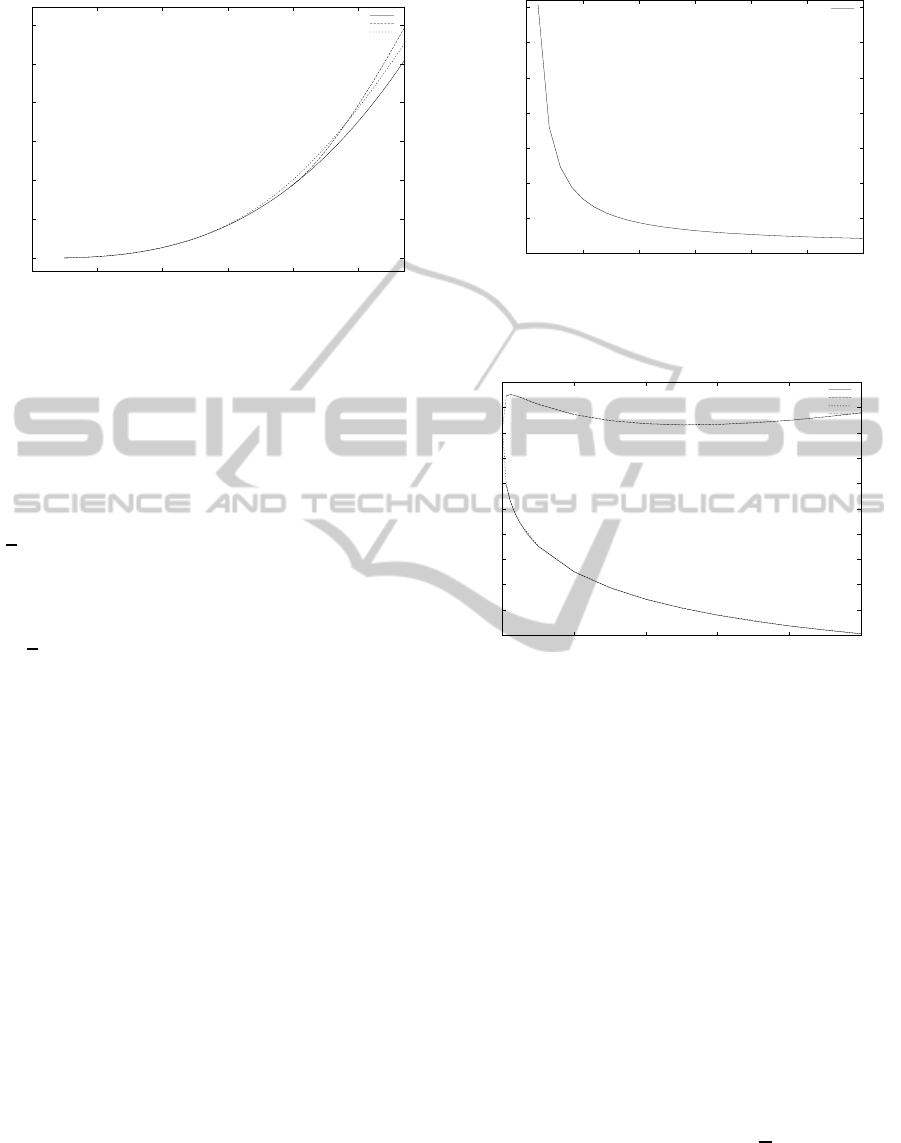
Next we show results for when we apply our
method to the CIR process. In figure 4, we plot the
values of P
L
and P
H
for varying values of h. We
have noticed that the change in the values of P
H
and
P
L
are not high as we increase h and that is because
of the behaviour of the CIR process, since no mat-
ter how long is the lag period, the price will always
return to the mean therefore the effect of P
L
and P
H
does not change significantly as we increase h, where
both P
L
and P
H
decreases slowly, since as we increase
h it is more likely to reach the mean. On the other
hand, the effect of σ we can see in figure 5 on the
prices of P
H
and P
L
is relatively higher than h, since
as we increase the volatility, the price increases. Con-
sequently the values P
L
and P
H
decreases, where as
we increase σ significently, both P
L
and P
H
goes to
zero because of the CIR property (σ
√
Pdt). However,
we believe that to model mean reversion process like
some commodities, the price of the product P will re-
turn to the mean eventually. Therefore, the investor
must not start the investment once it reaches the price
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
286

0.75
0.8
0.85
0.9
0.95
1
1.05
1.1
1.15
1.2
1.25
0 2 4 6 8 10
PL
PH
P
h
Figure 4: The values of P
L
of P
H
on CIR process using for
different values of h with κ = 0.01,Φ = 1.,ρ = .025,l =
0,k = 1,ω = 1,σ = 0.1.
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
PL
PH
P
σ
2
Figure 5: The values of P
L
of P
H
on CIR process using for
different values of σ
2
with κ = 0.01,Φ = 1., ρ = .025,l =
0,k = 1,ω = 1,h = 6.
of P
H
, before the price of the product stays around this
price for a longer period. In otherwords, the invest-
ment lag model with mean reversion process should
be modelled as Parisian option rather than European
option as we did in this paper. The application of the
Parisian option will be studied in future time.
6 CONCLUSIONS
In conclusion, we solved the problem for we have
showed a new methodology using a mixture of
Quadrature method and finite difference method with
a body-fitted co-ordinate algorithm to solve an invest-
ment lag problem presented in (Bar-Ilan and Strange,
1996) and with a very high convergence rate and
an acceptable speed of computing. Additionally, we
have shown the the results presented in this paper are
as accurate as the results presented in (Sødal, 2006)
for the GBM process. Moreover, we have applied this
model on other stochastic process such as CIR mean
reversion process and have shown the results.
REFERENCES
Andricopoulos, A. D., Widdicks, M., Duck, P.W., and New-
ton, D. P. (2003). Universal option valuation using
quadrature methods. Journal of Financial Economics,
67(3):447–471.
Bar-Ilan, A. and Strange, W. C. (1996). Investment lags.
The American Economic Review, 86(3):pp. 610–622.
Brekke, K. A. and Øksendal, B. (1994). Optimal switching
in an economic activity under uncertainty. SIAM Jour-
nal on Control and Optimization, 32(4):1021–1036.
Brennan, M. J. and Schwartz, E. S. (1985). Evaluating nat-
ural resource investments. The Journal of Business,
58(2):pp. 135–157.
Costeniuc, M., Schnetzer, M., and Taschini, L. (2008). En-
try and exit decision problem with implementation de-
lay. Journal of Applied Probability, 45(4):1039–1059.
Gauthier, L. and Morellec, E. (2000). Investment under un-
certainty with implementation delay. New Develop-
ments and Applications in Real Options.
MacRae, K. (1989). Critical issues in electric power plan-
ning in the 1990s: executive summary. Canadian En-
ergy Research Institute, 1(1):42–105.
Myers, S. C. (1977). Determinants of corporate borrowing.
Journal of financial economics, 5(2):147–175.
Senate, U. (2002). Gas prices: How are they really set. Re-
port prepared by the Majority Staff of the Permanent
Subcommittee on Investigations, released in conjunc-
tion with the Permanent Subcommittee on Investiga-
tions? Hearings on April, 30.
Sødal, S. (2006). Entry and exit decisions based on a dis-
count factor approach. Journal of Economic Dynam-
ics and Control, 30(11):1963–1986.
InvestmentLags-ANumericalApproach
287
