Dynamic Heterogeneous Multi-Population Cultural Algorithm for Large

Scale Global Optimization

Mohammad R. Raeesi N. and Ziad Kobti

School of Computer Science, University of Windsor, Windsor, ON, Canada

Keywords:

Cultural Algorithm, Multi-Population, Heterogeneous Sub-population, Dynamic Decomposition, Large Scale

Global Optimization.

Abstract:

Dynamic Heterogeneous Multi-Population Cultural Algorithm (D-HMP-CA) is a novel algorithm to solve

global optimization problems. It incorporates a number of local Cultural Algorithms (CAs) and a shared

belief space. D-HMP-CA beneﬁts from its dynamic decomposition techniques including the bottom-up and

top-down strategies. These techniques divide the problem dimensions into a number of groups which will be

assigned to different local CAs. The goal of this article is to evaluate the algorithm scalability. In order to do

so, D-HMP-CA is applied on a benchmark of large scale global optimization problems. The results show that

the top-down strategy outperforms the bottom-up technique by offering better solutions, while within lower

size optimization problems the bottom-up approach presents a better performance. Generally, this evaluation

reveals that D-HMP-CA is an efﬁcient method for high dimensional optimization problems due to its compu-

tational complexity for both CPU time and memory usage. Furthermore, it is an effective method such that it

offers competitive solutions compared to the state-of-the-art methods.

1 INTRODUCTION

Optimization problems are a set of problems where

the goal is to make a system as effective as possible.

Minimizing the total assembly cost of a huge com-

puter system and maximizing the resource utilization

within a manufacturing system are two samples of op-

timization problems. The goal of this research area is

to design an algorithm to be able to ﬁnd the optimal

solution within an acceptable time. In other words, an

optimization algorithm should be effective in terms of

ﬁnding optimal solutions and it is expected to be efﬁ-

cient in terms of the resources it requires to converge

to the optimal solution.

The research area of optimization is very well-

known due to its wide range of applications within

both continuous and discrete problem domains. The

problems within continuous domains are called global

optimization problems. The focus of this paper is to

deal with large scale global optimization problems in

which the number of problem dimensions is a large

number.

To solve optimization problems, different kinds of

algorithms are introduced in the literature. Cultural

Algorithm (CA) developed by Reynolds (Reynolds,

1994) is a subset of population-based methods which

are successfully applied to deal with optimization

problems. CA incorporates knowledge to guide its

search mechanism. CA incorporates two spaces in-

cluding population space and belief space such that

the former one is responsible for evolving solutions

and the latter one is designed to extract, update and

record the knowledge over generations.

The most recent architecture to implement CAs

is Heterogenous Multi-Population Cultural Algorithm

(HMP-CA) (Raeesi N. and Kobti, 2013) in which

the given problem is decomposed into a number of

sub-problems and sub-problems are assigned to dif-

ferent local CAs to get optimized separately in paral-

lel. HMP-CA (Raeesi N. et al., 2014) is designed to

deal with only static dimension decomposition tech-

niques, but its improved version, Dynamic HMP-CA

(D-HMP-CA) (Raeesi N. and Kobti, 2014), covers

dynamic decomposition techniques as well. Although

D-HMP-CA offers a great performance to solve nu-

merical optimization functions, there is no informa-

tion reported regarding its scalability to show its per-

formance on high dimensional problems. In this ar-

ticle, the performance of D-HMP-CA on large scale

global optimization problems is evaluated in terms of

both effectiveness and efﬁciency.

The remaining of this article is structured as fol-

184

Raeesi N. M. and Kobti Z..

Dynamic Heterogeneous Multi-Population Cultural Algorithm for Large Scale Global Optimization.

DOI: 10.5220/0005068801840191

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 184-191

ISBN: 978-989-758-052-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

lows. Section 2 brieﬂy describes HMP-CA and the

existing dimension decomposition techniques, fol-

lowed by representing large scale global optimization

in Section 3. D-HMP-CA and its dynamic decompo-

sition techniques are characterized with more details

in Section 4. Section 5 illustrates conducted experi-

ments, results and their corresponding discussion. Fi-

nally Section 6 represents concluding remarks and fu-

ture directions.

2 RELATED WORK

HMP-CA (Raeesi N. and Kobti, 2013) incorporates

only one belief space which is shared among its local

CAs instead of one local belief space for each local

CA. The shared belief space records the best parame-

ters found for each dimension.

The local CAs within this architecture are de-

signed to optimize different subsets of problem di-

mensions. Therefore, HMP-CA requires a dimension

decomposition technique which has a major effect

on the algorithm performance. The ﬁrst HMP-CA

(Raeesi N. and Kobti, 2013) incorporates a static di-

mension decomposition approach. The static decom-

position techniques are the ones in which the number

of dimension groups is predeﬁned and the dimensions

are assigned to a group initially such that they are not

going to be re-assigned to another group later.

The effects of different decomposition techniques

on the algorithm performance are also evaluated by

incorporating a number of static decomposition tech-

niques which can be categorized into two groups

of balanced and imbalanced approaches (Raeesi N.

et al., 2014). The former approaches assign the same

number of dimensions to the local CAs, while the

techniques in the latter group assign different num-

bers of problem dimensions to different local CAs.

The results of this evaluation reveal that the im-

balanced techniques highly outperform the balanced

ones in terms of both effectiveness and efﬁciency. The

point is that assigning one dimension to each local

CA results in a better performance in solving fully-

separable problems, while assigning a number of di-

mensions to each local CA works better for solving

non-separable problems. Therefore, the imbalanced

techniques which cover both types of assignments re-

sult in a better performance compared to the balanced

techniques.

HMP-CA is further improved by incorporat-

ing dynamic dimension decomposition techniques

(Raeesi N. and Kobti, 2014). D-HMP-CA introduces

two different dynamic approaches called top-down

and bottom-up strategies. In this article, the perfor-

mance of these techniques to solve high dimensional

problems is evaluated and compared with the state-of-

the-art methods.

Dimension decomposition is also incorporated by

another MP-CAs called Cultural Cooperative Parti-

cle Swarm Optimization (CCPSO) (Lin et al., 2009).

In CCPSO, each dimension is assigned to one local

CA such that it needs D local CAs to solve a D-

dimensional optimization problem. CCPSO incorpo-

rates Particle Swarm Optimization (PSO) within each

local CA to evolve its sub-population.

Dimension decomposition techniques are also

well-known in other research areas specially in the

area of Cooperative Coevolution (CC) (Potter and

De Jong, 1994). CC introduces a framework incor-

porating a divide-and-conquer approach such that it

decomposes a problem into a number of smaller sub-

problems. Then each sub-problem is getting opti-

mized by an EA separately in parallel. Although

both CC and HMP-CA have the similar frameworks,

HMP-CA has an additional component compared

to CC, namely its belief space, which incorporates

knowledge to improve the search mechanism.

The ﬁrst CC algorithm which is called Coop-

erative Co-evolutionary Genetic Algorithm (CCGA)

(Potter and De Jong, 1994) incorporates the same

dimension decomposition technique as CCPSO (Lin

et al., 2009). This approach is also used in the ﬁrst at-

tempt for applying CC to large scale global optimiza-

tion (Liu et al., 2001).

Another well-known decomposition technique is

cooperative split algorithm (van den Bergh and Engel-

brecht, 2000; Olorunda and Engelbrecht, 2009) which

initially decomposes a problem into K sub-problems

by considering almost the same number of dimen-

sions for each sub-problem. The K parameter is re-

ferred by split factor in this algorithm.

Random grouping is also another decomposition

technique which is introduced in DECC-G algo-

rithm (Yang et al., 2008a). In random grouping,

a D-dimensional problem is decomposed into m s-

dimensional problems satisfying m×s = D. Although

the number of dimension groups is constant in this

strategy, the groups are dynamic such that the dimen-

sions are re-assigned to different groups every cycle.

Since it is using a constant group size, selecting the

best group size is the main limitation of DECC-G due

to the fact that for separable problems it works bet-

ter with a smaller group size, while for non-separable

problems it works better with a larger group size.

Multilevel Cooperative Coevolution (MLCC)

(Yang et al., 2008b; Li and Yao, 2012) solved the

limitation of DECC-G by incorporating a multilevel

strategy for selecting a group size. A pool of different

DynamicHeterogeneousMulti-PopulationCulturalAlgorithmforLargeScaleGlobalOptimization

185

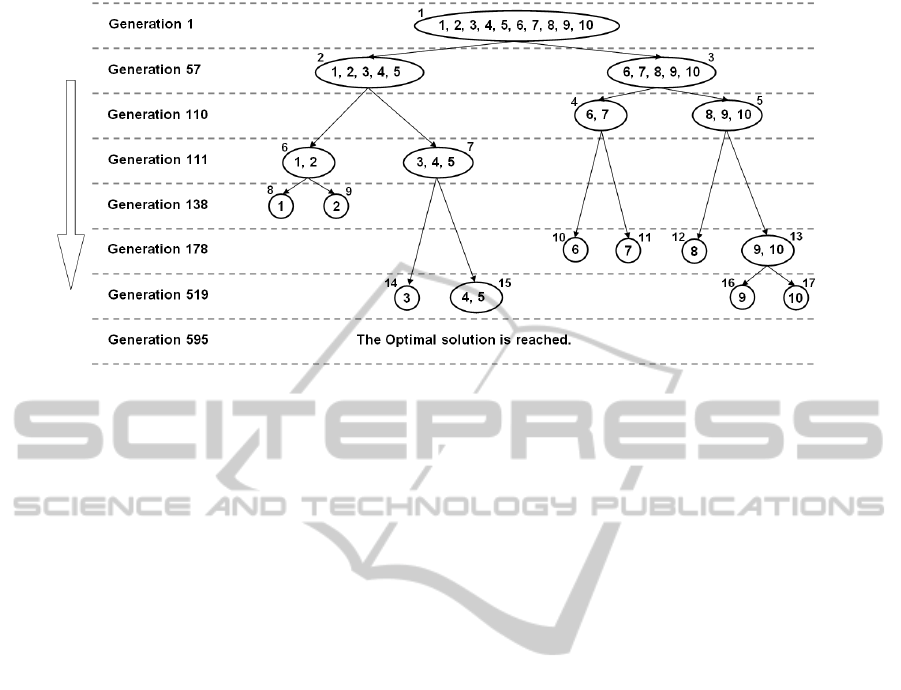
Figure 1: A sample run of the dynamic top-down approach on a 10-dimensional generalized Rosenbrock’s function ( f

group sizes are deﬁned within MLCC and it selects

one group size based on the problem under investiga-

tion and the stage of the evolution. Incorporating the

pool strategy outperforms DECC-G, but determining

a good pool of group sizes is remained as an issue

with MLCC.

Considering variable interactions in designing di-

mension decomposition technique may results in a

better performance. Cooperative Coevolution with

Variable Interaction Learning (CCVIL) (Chen et al.,

2010) beneﬁts from a module called Variable Interac-

tion Learning (VIL) to detect the dimensions interde-

pendencies. Although VIL module improves the op-

timization process by merging interdependent dimen-

sions into one group and preserve the independent di-

mensions within different groups, it is computation-

ally expensive which limits its applicability.

Omidvar et al. (Omidvar et al., 2010) introduced

a systematic approach to detect interacting variables

in their proposed DECC-DML algorithm. Their pro-

posed module which is called delta grouping consid-

ers the low-improved dimensions to be interacting.

Although this kind of detection is not precise, there

is no major computational cost associated with it.

3 LARGE SCALE GLOBAL

OPTIMIZATION

As described before, numerical optimization is a sub-

set of global optimization problems in which there is a

mathematical function to be optimized. In numerical

optimization, the given function should be considered

as a black box such that it gets a D-dimensional vec-

tor of real numbers as input and returns a real num-

ber as the objective value for the given vector. Gen-

eralized Rosenbrock’s function which is presented in

Equation 1 is a sample numerical optimization func-

tion with both upper and lower bounds constraints on

each dimension.

(X) =

D−1

∑

i=1



100



i+1

− x



+ (x

− 1)



(1)

Constraints : ∀i ∈

{

1,...,D

}

− 30 ≤ x

≤ 30

Optimum : min( f

) = f

(< 1, ..., 1 >) = 0

The high dimensional numerical optimization

problems are also known as large scale global op-

timization. One of the well-known benchmarks for

high dimensional problems is the benchmark of the

CEC’2010 competition on large scale global opti-

mization (Tang et al., 2009) which includes twenty

1000-dimensional numerical optimization functions.

Although recently other benchmarks are introduced

for high dimensional problems, this benchmark is se-

lected due to its usage in evaluating related methods.

4 DYNAMIC HMP-CA

Dynamic HMP-CA (D-HMP-CA) (Raeesi N. and

Kobti, 2014) is the improved version of HMP-CA

which is capable to deal with dynamic decomposi-

tion techniques. During the process of evolution, it

generates new local CAs and assigns them different

dimension subsets. D-HMP-CA incorporates two dif-

ferent dynamic approaches including bottom-up and

top-down techniques which are further characterized

with examples in the following sub-sections.

D-HMP-CA is evaluated over twelve 30-

dimensional benchmark functions (Raeesi N. and

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

186

Figure 2: A sample run of the dynamic bottom-up approach on a 10-dimensional generalized Rosenbrock’s function ( f

Kobti, 2014). The evaluation results reveal that for

both dynamic techniques, D-HMP-CA presents a

very good performance such that it is able to ﬁnd the

optimal solutions for every single run. However, in

terms of algorithm efﬁciency, the results show that

the bottom-up approach is more efﬁcient due to its

better convergence rate. In this article, D-HMP-CA is

applied on large scale global optimization problems

to be evaluated in terms of algorithm scalability.

D-HMP-CA incorporates two algorithm parame-

ters which are as follows:

• PopSize: The sub-population size of local CAs.

• NoImpT : A threshold for the number of genera-

tions a local CA cannot ﬁnd a better solution.

These parameters are adjusted by conducting exten-

sive experiments, the results of which show that the

algorithm works better generally over all the consid-

ered problems by assigning 10 and 5 to PopSize and

NoImpT , respectively (Raeesi N. and Kobti, 2014).

4.1 Dynamic Top-Down Dimension

Decomposition Technique

The top-down technique starts with a local CA de-

signed to optimize all the problem dimensions to-

gether. When the local CA cannot ﬁnd a better so-

lution after NoImpT generations, it will be split and

two new local CAs will be generated, each of which is

designed to optimize one half of the dimensions of its

parent. It should be noted here that the decomposed

local CA cooperates with the two new local CAs for

the next generations such that the decomposed local

CA will not be split again. Local CAs with only one

assigned dimension will not be decomposed as well.

Figure 1 illustrates a sample run of D-HMP-

CA with the proposed top-down dimension decom-

position approach on a 10-dimensional generalized

Rosenbrock’s function ( f

) represented in Equation 1.

In this experiment, PopSize and NoImpT parameters

are set to 10 and 5, respectively. The ﬁgure shows that

the proposed method starts with a local CA designed

to optimize all the 10 dimensions. In generation 57,

the local CA reaches to its 5

generation that it can-

not ﬁnd a better solution. Therefore, it will be split

into two new local CAs 2 and 3 with assigned dimen-

sions (1,2,3,4,5) and (6,7,8,9,10), respectively. These

three local CAs continue to optimize their assigned

dimensions until generation 110 in which the 3rd lo-

cal CA gets ready to be split. This routine continues

until generation 595 in which the optimal solution is

obtained. It should be noted that the optimal solution

is reached without requiring local CA 15 to be split.

4.2 Dynamic Bottom-Up Dimension

Decomposition Technique

The bottom-up approach starts with a number of lo-

cal CAs, each of which is designed to optimize only

one dimension. The number of initially generated lo-

cal CAs equals to the number of problem dimensions.

These local CAs starts to optimize their assigned di-

mensions until two of them reach to the no improve-

ment threshold. In this stage, a new local CA is gener-

ated to optimize all the dimensions of those two local

CAs. Like the top-down approach, each local CA is

merged only one time. Therefore, a local CA with all

the problem dimensions never get merged.

Similar to the top-down technique, D-HMP-CA

with the bottom-up approach is applied on a 10-

dimensional generalized Rosenbrock’s function ( f

)

with the same parameters. As illustrated in Figure 2,

the proposed HMP-CA starts with 10 local CAs, each

of which is designed to optimize only one dimension.

DynamicHeterogeneousMulti-PopulationCulturalAlgorithmforLargeScaleGlobalOptimization

187

Table 1: The results of applying D-HMP-CA incorporating two different dynamic approaches on CEC’2010 benchmark

functions for large scale global optimization (Tang et al., 2009)

Functions

Bottom-Up Top-Down

Evolved Dimensions

Mean Std Dev

Evolved Dimensions

Mean Std Dev

Total In Average Total In Average

1.36E+07 4.54 4.04E-06 1.23E-05 1.95E+07 6.51 3.69E+05 1.43E+06

1.28E+07 4.28 1.99E-10 2.15E-10 2.00E+07 6.67 9.68E-11 8.93E-11

1.16E+07 3.88 1.92E-07 1.32E-07 1.94E+07 6.46 6.90E-06 2.59E-05

1.35E+07 4.51 3.01E+12 1.18E+12 2.01E+07 6.70 1.42E+11 3.75E+11

1.43E+07 4.76 1.94E+08 1.68E+08 1.96E+07 6.54 3.72E+07 2.79E+07

1.43E+07 4.78 5.32E+06 8.10E+05 1.93E+07 6.43 4.80E+06 5.24E+05

1.38E+07 4.59 4.98E+08 2.92E+08 2.02E+07 6.73 3.91E+06 9.09E+06

1.50E+07 5.00 5.94E+07 5.38E+07 2.02E+07 6.74 2.29E+07 3.42E+07

1.38E+07 4.59 2.93E+07 2.91E+06 2.02E+07 6.74 2.11E+05 3.70E+04

1.43E+07 4.76 4.13E+03 2.06E+02 2.01E+07 6.71 7.68E+01 3.03E+01

1.43E+07 4.78 5.82E+01 6.64E+00 1.90E+07 6.35 5.46E+01 6.35E-01

8.94E+06 2.98 1.23E+04 2.08E+03 1.99E+07 6.63 1.17E+01 4.43E+00

1.39E+07 4.63 9.96E+02 5.77E+02 2.09E+07 6.96 3.75E+02 1.57E+02

9.30E+06 3.10 6.89E+07 5.32E+06 2.01E+07 6.72 4.43E+05 5.24E+04

1.43E+07 4.77 1.19E+03 2.38E+03 2.01E+07 6.70 1.86E+02 1.70E+02

1.44E+07 4.79 1.13E+02 7.86E+00 1.90E+07 6.33 1.09E+02 1.25E+00

8.46E+06 2.82 3.50E+04 4.97E+03 1.98E+07 6.60 5.07E+01 2.19E+01

1.34E+07 4.48 1.82E+03 2.45E+02 2.09E+07 6.98 6.52E+02 2.11E+02

9.89E+06 3.30 3.79E+05 5.17E+04 2.01E+07 6.71 8.88E+03 8.86E+03

1.35E+07 4.48 1.24E+03 1.41E+02 2.11E+07 7.02 1.04E+03 2.52E+02

Average 1.29E+07 4.29 2.00E+07 6.66

They continue optimizing their assigned dimension

until generation 40 when local CAs 9 and 10 reach

to their no improvement threshold. Therefore, a new

local CA is generated to optimize their assigned di-

mensions concurrently which would be local CA 11

with dimensions (9,10). In the next generation, local

CAs 1 and 2, 3 and 4, and 5 and 6 are merged together

and generate local CAs 12, 13, and 14, respectively.

This routine continues until generation 65 in which a

local CA with all the 10 problem dimensions is gen-

erated. These 19 local CAs continue to optimize their

own assigned dimensions until generation 650 when

an optimal solution is found.

In addition to these dynamic decomposition tech-

niques, D-HMP-CA incorporates a shared belief

space of size 3 which inﬂuences the search mecha-

nism only by providing complement parameters for

evaluating partial solutions. In D-HMP-CA, each lo-

cal CA uses a simple DE incorporating DE/rand/1

mutation operator, binomial crossover operator and a

selection mechanism (Raeesi N. and Kobti, 2013).

5 EXPERIMENTS AND RESULTS

The D-HMP-CA incorporating both dynamic decom-

position techniques is experimented on the CEC’2010

benchmark for large scale global optimization prob-

lems (Tang et al., 2009). This benchmark provides

some rules and regulations which are as follows. The

number of dimensions for all 20 optimization func-

tions should be set to 1000. Although the maximum

number of ﬁtness evaluations is 3.00E+6, the obtained

solutions for 1.20E+5 and 6.00E+5 ﬁtness evaluations

should be recorded. Furthermore, it is declared that

each experiment should be conducted for 25 indepen-

dent runs.

The results of applying D-HMP-CA on CEC’2010

benchmark (Tang et al., 2009) are presented in Ta-

ble 1 illustrating the mean and the standard devia-

tion of the solutions obtained for 25 independent runs.

The better mean value is emphasized with bold face

The results presented in these tables reveal that the

top-down approach offers better results such that it

can ﬁnd better solutions for all optimization functions

except two functions f

and f

. Therefore, the re-

sults indicate that although the bottom-up approach

presents better performance in small scale optimiza-

tion problems (Raeesi N. and Kobti, 2014), the top-

down approach is a more effective method in high di-

mensional problems. This could be due to the fact

that in the earlier generations the local CAs are look-

ing for the promising regions and this is happening

by lower number of local CAs with higher number

To see the more detailed results includ-

ing the solutions obtained by 1.20E+5 and

6.00E+5 ﬁtness evaluations please refer to

http://cs.uwindsor.ca/~raeesim/ECTA2014/AllResults.pdf

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

188

of dimensions in the top-down approach, while in the

bottom-up approach it takes the resources of higher

number of local CAs with lower number of dimen-

sions. Therefore, it is expected for the top-down ap-

proach to have more resources (ﬁtness evaluations)

for exploiting the promising regions which results in

its better performance for non-separable optimization

functions. Conversely for the fully separable func-

tions, the top-down approach uses too much resources

to generate the local CAs with only one assigned di-

mensions, while the bottom-up approach starts by ini-

tializing these local CAs. This could be the main

reason which makes the bottom-up approach a bet-

ter strategy for functions f

and f

and a competitive

approach for function f

D-HMP-CA is also evaluated in terms of efﬁ-

ciency to deal with high dimensional problems. D-

HMP-CA incorporates the concept of partial solution

which is a solution including values for a number of

dimensions instead of for all the problem dimensions.

D-HMP-CA design each sub-population to handle the

partial solutions including the values for the dimen-

sions assigned to the corresponding local CA. In these

experiments, 3.00E+6 partial solutions are evolved

over various generations such that the numbers of di-

mensions within these partial solutions are different.

One partial solution, for instance, may have only one

dimension while another one may have up to 1000 di-

mensions.

The total number of dimensions within 3.00E+6

partial solutions are counted for all the experiments.

The total number of dimensions is averaged over the

25 independent runs which is represented in Table 1.

For instance, the average total number of dimensions

incorporated by the bottom-up strategy to solve opti-

mization function f

is 1.36E+07. Since this number

of dimensions are incorporated by 3.00E+6 partial so-

lutions, it can be said that a partial solution in these

experiments incorporates 4.54 dimensions in average.

Table 1 also illustrates the average number of dimen-

sions for one partial solution.

Averaged over all the optimization functions, the

bottom-up strategy in average incorporates 4.29 di-

mensions within one partial solution, while the top-

down approach incorporates 6.66 dimensions. This

difference is mainly due to the fact the top-down strat-

egy starts with partial solutions with higher number of

dimensions compared to the bottom-up approach.

Considering 3 operations to be calculated for the

DE/rand/1 mutation operator and 3.00E+6 solu-

tions to be mutated, an algorithm requires to execute

6.00E + 6 × #Dimensions operations in total where

#Dimensions denotes the number of dimensions of a

sample solution.

#TotalOperations

= 3 Operations × #TotalDimensions

= 3 × (3.00E + 6) Solutions × #Dimensions

= 9.00E + 6 × #Dimensions

Therefore, based on this calculation if an algorithm

works with only complete solutions, it needs to calcu-

late 9.00E+9 operations, while the number of opera-

tions required by the bottom-up and top-down strate-

gies are only 3.86E+7 and 6.00E+7, respectively.

Comparing 9.00E+9 operations with 3.87E+7 and

5.99E+7 operations shows that the efﬁciency of calcu-

lating the mutation operator is improved by more than

99%. The same improvement is also obtained for the

crossover operator. Conversely, the concept of partial

solutions does not affect the efﬁciency of the selection

mechanism in which the new partial solutions are re-

quired to be completed for their evaluation.

In order to evaluate the effectiveness of D-HMP-

CA, its results on large scale global optimization

problems are compared with the results of the state-

of-the-art methods including DECC-G (Yang et al.,

2008a), MLCC (Yang et al., 2008b), DECC-DML

(Omidvar et al., 2010) and CCVIL (Chen et al., 2010).

These methods are considered for the comparison due

to the fact that they are the most recent methods in-

troducing new dimension decomposition techniques.

The results of this comparison which is represented in

Table 2 illustrate the corresponding rank obtained by

both versions of D-HMP-CA compared to the state-

of-the-art methods. The best results are also empha-

sized with bold face. In order to statistically evalu-

ate this comparison, a non-parametric procedure is in-

corporated (Garca et al., 2009) which includes Fried-

man’s ranking test followed by Bonferroni-Dunns test

with the two most common signiﬁcance levels in the

literature which are α = 0.05 and α = 0.10.

The Friedman’s statistic value of Friedman’s rank-

ing test is 28.57, for which the p-value in a chi-

squared distribution is less than 0.0001. It means

that there are signiﬁcant differences between the com-

pared algorithms. These differences will be deter-

mined by the second part of this statistical analysis.

In order to do so, the algorithm with the minimum av-

erage rank should be selected as the control algorithm.

In this case, the control algorithm would be our pro-

posed D-HMP-CA with the top-down strategy. With

respect to each signiﬁcance level, Bonferroni-Dunns

test calculates a critical difference (CD) for the con-

trol algorithm, the results of which are as follows:

CD =



1.5240 for α = 0.05

1.3761 for α = 0.10

DynamicHeterogeneousMulti-PopulationCulturalAlgorithmforLargeScaleGlobalOptimization

189

Table 2: Comparing the results of applying D-HMP-CA with both dynamic approaches on CEC’2010 benchmark functions

for large scale global optimization (Tang et al., 2009) with state-of-the-art methods.

Functions

DECC-G MLCC DECC-DML CCVIL

D-HMP-CA

Bottom-Up Top-Down

Mean Mean Mean Mean Mean Rank Mean Rank

2.93E-07 1.53E-27 1.93E-25 1.55E-17 4.04E-06 5 3.69E+05 6

1.31E+03 5.55E-01 2.17E+02 6.71E-09 1.99E-10 2 9.68E-11 1

1.39E+00 9.86E-13 1.18E-13 7.52E-11 1.92E-07 4 6.90E-06 5

5.00E+12 1.70E+13 3.58E+12 9.62E+12 3.01E+12 2 1.42E+11 1

2.63E+08 3.84E+08 2.99E+08 1.76E+08 1.94E+08 3 3.72E+07 1

4.96E+06 1.62E+07 7.93E+05 2.94E+05 5.32E+06 5 4.80E+06 3

1.63E+08 6.89E+05 1.39E+08 8.00E+08 4.98E+08 5 3.91E+06 2

6.44E+07 4.38E+07 3.46E+07 6.50E+07 5.94E+07 4 2.29E+07 1

3.21E+08 1.23E+08 5.92E+07 6.66E+07 2.93E+07 2 2.11E+05 1

1.06E+04 3.43E+03 1.25E+04 1.28E+03 4.13E+03 4 7.68E+01 1

2.34E+01 1.98E+02 1.80E-13 3.48E+00 5.82E+01 5 5.46E+01 4

8.93E+04 3.48E+04 3.80E+06 8.95E+03 1.23E+04 3 1.17E+01 1

5.12E+03 2.08E+03 1.14E+03 5.72E+02 9.96E+02 3 3.75E+02 1

8.08E+08 3.16E+08 1.89E+08 1.74E+08 6.89E+07 2 4.43E+05 1

1.22E+04 7.10E+03 1.54E+04 2.65E+03 1.19E+03 2 1.86E+02 1

7.66E+01 3.77E+02 5.08E-02 7.18E+00 1.13E+02 5 1.09E+02 4

2.87E+05 1.59E+05 6.54E+06 2.13E+04 3.50E+04 3 5.07E+01 1

2.46E+04 7.09E+03 2.47E+03 1.33E+04 1.82E+03 2 6.52E+02 1

1.11E+06 1.36E+06 1.59E+07 3.52E+05 3.79E+05 3 8.88E+03 1

4.06E+03 2.05E+03 9.91E+02 1.11E+03 1.24E+03 4 1.04E+03 2

Avg Rank 4.85 4.25 3.50 3.05 3.40 1.95

The summation of a CD and the average rank of

the control algorithm deﬁnes the threshold ranks with

respect to the corresponding signiﬁcance levels which

are as follows:

T hreshold Rank =



3.4740 for α = 0.05

3.3261 for α = 0.10

A threshold rank determines the algorithms which

are signiﬁcantly outperformed by the control algo-

rithm with respect to the corresponding signiﬁcance

level. In other words, this statistical procedure states

that the algorithms with average rank higher than a

threshold rank are signiﬁcantly outperformed by the

control algorithm with respect to the corresponding

signiﬁcance level. Figure 3 graphically depicts the re-

sults of this statistical analysis. In this ﬁgure, the solid

line and the dashed line represent the threshold ranks

for the signiﬁcance levels α = 0.05 and α = 0.10, re-

spectively. This ﬁgure indicates that the control algo-

rithm signiﬁcantly outperforms the algorithms whose

bar exceeds the threshold lines.

Therefore based on the Friedman’s ranking test

and Bonferroni-Dunn’s method, it can be stated that

the proposed D-HMP-CA with top-down strategy out-

performs DECC-G, MLCC and DECC-DML with the

signiﬁcance level α = 0.05 and it also outperforms

D-HMP-CA with bottom-up strategy with the signif-

icance level α = 0.10. Furthermore, this statistical

analysis states that although the results obtained by

D-HMP-CA with top-down strategy is better than the

results of CCVIL, the improvement is not signiﬁcant.

6 CONCLUSIONS

HMP-CA (Raeesi N. and Kobti, 2013) incorporates

a number of heterogeneous local CAs and a shared

belief space to deal with optimization problems. In

HMP-CA, the given problem is decomposed into a

number of sub-problems which are assigned to differ-

ent local CAs to be optimized separately in parallel.

HMP-CA is improved by incorporating dynamic

decomposition techniques (Raeesi N. and Kobti,

2014). The improved version which is called D-

HMP-CA introduces two dynamic techniques in-

cluding bottom-up and top-down strategies. It has

been shown that D-HMP-CA is an effective as well

as efﬁcient method to solve optimization problems

(Raeesi N. and Kobti, 2014).

In this article, the performance of D-HMP-CA is

evaluated over large scale global optimization. The

interesting point of this research study is that the top-

down strategy outperforms the bottom-up technique

by offering better solutions, while within lower size

problems the bottom-up approach presents a better

performance. Generally, the results of this evalua-

tion reveal that D-HMP-CA is an efﬁcient method

due to its computational complexity. Furthermore, it

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

190

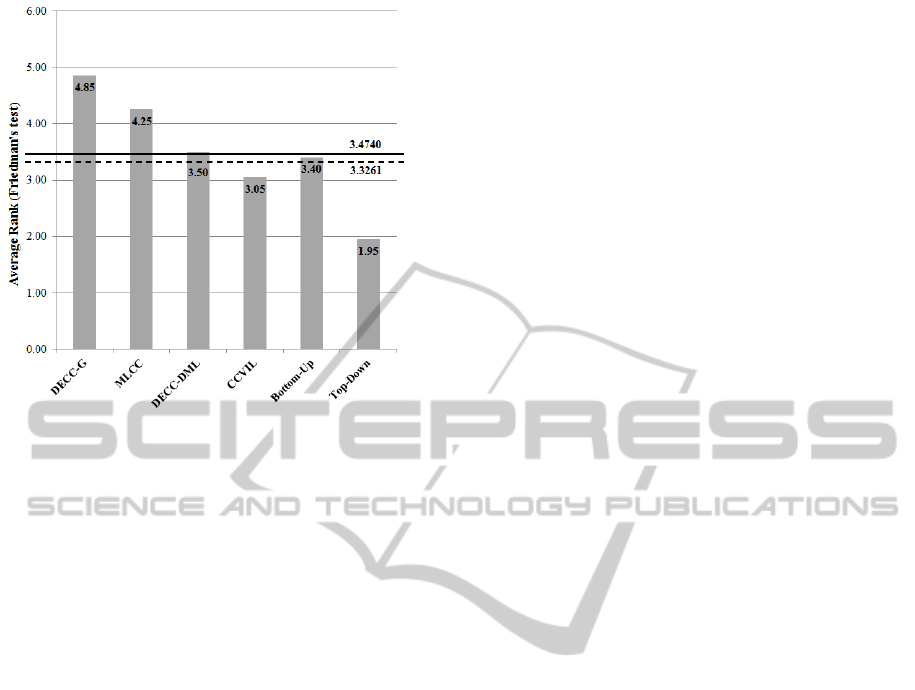
Figure 3: The Graphical Representation of Statistical Anal-

ysis with Friedman’s test and Bonferroni-Dunn’s method.

is proved that the proposed D-HMP-CA is a scalable

method such that it offers competitive performance to

solve large scale global optimization problems com-

pared to the state-of-the-art methods.

Although D-HMP-CA offers a great performance

to solve large scale global optimization problems, it

can be further improved by incorporating more ad-

vanced decomposition strategies. Detecting variable

interactions in dimension decomposition approach is

considered as future direction for this research.

ACKNOWLEDGEMENTS

This work is made possible by the support from

the National Science Foundation under Grant DEB-

0816400 and NSERC Discovery under Grant No.

327482.

REFERENCES

Chen, W., Weise, T., Yang, Z., and Tang, K. (2010). Large-

scale global optimization using cooperative coevo-

lution with variable interaction learning. In Paral-

lel Problem Solving from Nature (PPSN XI), volume

6239, pages 300–309.

Garca, S., Molina, D., Lozano, M., and Herrera, F. (2009).

A study on the use of non-parametric tests for ana-

lyzing the evolutionary algorithms’ behaviour: A case

study on the cec’2005 special session on real parame-

ter optimization. Journal of Heuristics, 15:617–644.

Li, X. and Yao, X. (2012). Cooperatively coevolving parti-

cle swarms for large scale optimization. IEEE Trans-

actions on Evolutionary Computation, 16 (2):210–

224.

Lin, C.-J., Weng, C.-C., Lee, C.-L., and Lee, C.-Y.

(2009). Using an efﬁcient hybrid of cooperative par-

ticle swarm optimization and cultural algorithm for

neural fuzzy network design. In International Con-

ference on Machine Learning and Cybernetics, pages

3076–3082.

Liu, Y., Yao, X., Zhao, Q., and Higuchi, T. (2001). Scal-

ing up fast evolutionary programming with coopera-

tive coevolution. In IEEE Congress on Evolutionary

Computation (CEC), pages 1101–1108.

Olorunda, O. and Engelbrecht, A. (2009). An analysis

of heterogeneous cooperative algorithms. In IEEE

Congress on Evolutionary Computation (CEC), pages

1562–1569.

Omidvar, M. N., Li, X., and Yao, X. (2010). Cooperative

co-evolution with delta grouping for large scale non-

separable function optimization. In IEEE Congress on

Computational Intelligence (CEC), pages 1–8.

Potter, M. and De Jong, K. (1994). A cooperative coevolu-

tionary approach to function optimization. In The 3rd

Conference on Parallel Problem Solving from Nature

(PPSN), volume 2, pages 249–257.

Raeesi N., M. R., Chittle, J., and Kobti, Z. (2014). A new

dimension division scheme for heterogenous multi-

population cultural algorithm. In The 27th Florida

Artiﬁcial Intelligence Research Society Conference

(FLAIRS-27), Pensacola Beach, FL, USA.

Raeesi N., M. R. and Kobti, Z. (2013). Heteroge-

neous multi-population cultural algorithm. In IEEE

Congress on Evolutionary Computation (CEC), pages

292–299, Cancun, Mexico.

Raeesi N., M. R. and Kobti, Z. (2014). Heterogeneous

multi-population cultural algorithm with a dynamic

dimension decomposition strategy. In The 27th Cana-

dian Conference on Artiﬁcial Intelligence (Canadian

AI), Montreal, QC, Canada. (To Be Appeared).

Reynolds, R. G. (1994). An introduction to cultural algo-

rithms. In Sebald, A. V. and Fogel, L. J., editors,

Thirs Annual Conference on Evolutionary Program-

ming, pages 131–139, River Edge, New Jersey. World

Scientiﬁc.

Tang, K., Li, X., P.N., S., Yang, Z., and Weise, T. (2009).

Benchmark functions for the CEC’2010 special ses-

sion and competition on large scale global optimiza-

tion. Technical report, NICAL, USTC, Hefei, Anhui,

China.

van den Bergh, F. and Engelbrecht, A. (2000). Coopera-

tive learning in neural networks using particle swarm

optimizers. South African Computer Journal, pages

84–90.

Yang, Z., Tang, K., and Yao, X. (2008a). Large scale evo-

lutionary optimization using cooperative coevolution.

Information Sciences, 178 (15):2985–2999.

Yang, Z., Tang, K., and Yao, X. (2008b). Multilevel co-

operative coevolution for large scale optimization. In

IEEE Congress on Evolutionary Computation (CEC),

pages 1663–1670.

DynamicHeterogeneousMulti-PopulationCulturalAlgorithmforLargeScaleGlobalOptimization

191