Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes

Rapha

el Groscot and Laurent D. Cohen

University Paris-Dauphine, PSL Research University, CEREMADE, CNRS UMR 7534, 75016 Paris, France

Keywords:

Shape Space, Deformable Models, Generative 3D Modeling.

Abstract:

The systematic study of morphings for non parametric shapes suffers from ambiguities in deﬁning good general

morphings, such as the trade-off between plausibility and smoothness, above all under large topology changes.

In the recent years, only neural networks have offered a generic solution, using their latent space as a shape

prior. But these models are optimized for single shape reconstruction, giving little control on the generated

morphings. In this paper, we show how qualitatively similar results can be achieved when replacing neural

networks with a set of carefully crafted components: a style-content separation method via the ﬁtting of a

Deformable Voxel Grid, a similarity metric adapted to the extracted content, and a formulation of morphings

as minimal paths in a graph. While forgoing the automatic learning of a generative model, we still achieve

similar morphing capabilities. We performed various evaluations, quantitative analysis on the robustness of our

proposed method and on the quality of the results, and demonstrate the usefulness of each component. Finally,

we provide guidance on how manual intervention can improve quality. This is indeed possible since, unlike

neural networks, each component in our method is interpretable.

1 INTRODUCTION

In the literature, the study of shape morphings typi-

cally follows one of two assumptions: (a) both shapes

have a shared connectivity, generally because they em-

body the same type of shape (e.g. human or animal

bodies), and the goal is to ﬁnd a plausible movement

between two conﬁgurations; or (b) the two shapes are

considered in a vacuum, without external shape priors,

and the goal is to ﬁnd a deformation from one to the

other, which minimizes a certain distortion criteria (e.g.

for pairs of arbitrary shapes).

Given the creative opportunities of morphing for

computer graphics, it is desirable to develop methods

with a wider applicability. In the recent years, genera-

tive neural networks such as auto encoders and GANs

have not only proven powerful to generate realistic

3D shapes, in various formats (voxels, pointclouds,

or meshes), but also offer a latent space amenable to

shape interpolations. By design, this learned represen-

tation provides a shape prior, constraining generated

shapes to be similar to the training set. However, they

are generally not built nor trained towards the end of

producing meaningful morphings. Rather, their mor-

phing capabilities appear as a mere byproduct of latent

space interpolation. Most works relying on them fo-

cus their efforts on the quality and expressivity of the

outputs, as they are generally mainly evaluated on the

reconstruction of known shapes.

These generative models beneﬁt from their ability

to learn, without supervision, an invertible encoding

which brings similar shapes close together. We ex-

plore the possibility of achieving similar results with

traditional, explicit methods. Doing so, we simultane-

ously address the typical limitations of deep learning;

namely, the lack of interpretability, and the need for

expensive and powerful hardware capable of parallel

computing.

As a matter of fact, the present work stems from the

intuition that medium-sized datasets contain enough

shapes to express novel shapes as simple combina-

tions and deformations of the existing ones. As a

result, we seek to generate “good” morphings whose

intermediate states are existing shapes, up to a small

deformation. Moreover, we do not want to rely on any

class-speciﬁc parameterization.

To this end, we propose three interconnected com-

ponents:

a class-independent shape descriptor, relying on

a particular case of style and content separation,

which we named “cubiﬁction”;

a deformation metric compatible with this content

descriptor;

Groscot, R. and Cohen, L.

Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes.

DOI: 10.5220/0011680200003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 1: GRAPP, pages

98-109

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

a graph-based framework for ﬁnding minimal-

energy shape morphings.

The ﬁrst and second steps respectively provide

nodes and links to ultimately build a shape graph. It

can be seen as a discretized version of a latent space,

where the intermediate representation is not learned

but handcrafted in accordance with the strong symme-

tries found in certain shapes, such as chairs or tables.

As a matter of fact, our content descriptor derives from

a cubiﬁction of the shapes, which appears to consis-

tently locate the semantical parts of different shapes.

This is performed via the optimization of a De-

formable Voxel Grid (DVG), presented in Section 3.

Then, Section 4 explains the construction of a graph

shape-space which encapsulates the similarities in

terms of shape content. We then present experimental

results and evaluations in Section 5. Finally, Section 6

provides an extensive analysis of many design ele-

ments of our method, discussing the inﬂuence and

interactions of its different components.

2 RELATED WORK

Deep Learning and Shape Latent Spaces

In this area, use cases typically include one of the fol-

lowing tasks: shape processing and data augmentation

(Park et al., 2017; Fish et al., 2014; Kalogerakis et al.,

2012; Haibin et al., 2015; Li et al., 2017), shape pre-

diction from 2D data (Shin et al., 2018; Haibin et al.,

2015; Wu et al., 2016; Wang et al., 2018; Fan et al.,

2016), shape completion (Allen et al., 2003; Groueix

et al., 2018; Park et al., 2019), and latent space explo-

ration (Tulsiani et al., 2017; Wu et al., 2016; Li et al.,

2017; Achlioptas et al., 2017; Groscot et al., 2019;

Dubrovina et al., 2019).

Over the past years, generative models, using ar-

chitectures inspired by Variational Auto Encoders

(Kingma and Welling, 2013) and GANs (Goodfellow

et al., 2014), have been used for shape morphing, via

linear interpolations in the latent space. Works can

represent shapes in various formats, such as point-

clouds (Qi et al., 2016; Qi et al., 2017; Fan et al.,

2016; Achlioptas et al., 2017; Groscot et al., 2019),

voxels (Wu et al., 2016; Li et al., 2017; Dubrovina

et al., 2019), octrees (Tatarchenko et al., 2017), or 4D

particle dynamics (Niemeyer et al., 2019).

Other works, focusing on the prediction of a 3D

shape from a given image, used more speciﬁc represen-

tations such as surface patches (Groueix et al., 2018)

or deformed ellipsoids (Wang et al., 2018), but they

do not appear to offer a direct way of producing shape

morphings. More recently, networks predicting im-

plicit functions (Park et al., 2019; Hao et al., 2020)

appeared to allow smooth, arbitrary-topology meshes,

while being compatible with latent space interpola-

tions.

Deep learning approaches are based on the assump-

tion that learned descriptors, as opposed to handcrafted

ones, are better suited to capture the variability of natu-

ral signals. Moreover, generative models offer a latent

space amenable to the generation of new shapes. How-

ever, neural networks come with known limitations:

their lack of interpretability and their constraints to

converge to visually-pleasing results. As a matter of

fact, they typically require rich databases, powerful

GPUs, and suffer from long training times and difﬁcult

parameters tuning. All this makes reproducing the re-

sults of deep learning based methods hard, even when

a portion of the code is public.

Our work takes quite an opposite view, exploring

the possibility of achieving similar results without any

neural network. We show in fact that we can obtain

the same capabilities offered by generative networks’

latent spaces, by carefully handcrafting and designing

every component. As a result, we already generate

satisfying results even with modest datasets (around

500 shapes), and because every component has a clear

meaning, one can easily improve the desired outcome

by manual intervention.

In a way, this work ultimately consists in investigat-

ing what remains once those applications are stripped

from neural networks, in order to better understand the

speciﬁcities they bring.

Morphing Based on Deformations

The problem of realistic shape morphing was tackled

by (Gao et al., 2013) for human and animal bodies,

interpreting a collection of shapes as a deformation

space. By establishing shape correspondences, they

obtain a shape distance allowing them to express mor-

phings as a minimal path among clusters of similar

body poses. We adopt a framework similar to theirs,

while focusing on shapes which have varied topolo-

gies and no natural parameterization, such as chairs

and sofas, such that a morphing cannot be interpreted

as a mere deformation. Our work can be seen as a

derivation of the same ideas, but adapted to different

modalities, typically addressed by deep learning meth-

ods.

As far as they are concerned, instead of relying

on geometric generative models, shape deformation

is another popular choice to generate realistic shapes

at a small cost, leveraging the similarity between ob-

jects belonging to the same class. To parameterize

these deformations, most approaches (Hanocka et al.,

2018; Kurenkov et al., 2017) use the Free Form Defor-

Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes

mation (Sederberg and Parry, 1986), which arranges

control points on a regular volumetric grid, and then

uses cubic interpolation to distort the object as the

points move. The key differences with our model

are the following. First, they tackle different prob-

lems, such as partial shape alignment (Hanocka et al.,

2018) or shape reconstruction by deforming a tem-

plate (Kurenkov et al., 2017). Second, and most im-

portantly, their shape deformations are pair-speciﬁc,

trained to predict deformations between pairs (

(A,B)

where

is deformed into

). On the contrary, our

model provides a consistent shape cubiﬁction, without

any learning, allowing to compare all shapes (in terms

of similarity measure); and we use this representation

to estimate minimal-energy morphings.

More recently, (Zheng et al., 2020) showed how

to reconstruct shapes by deforming an implicit tem-

plate, predicted by a neural network, giving shape

correspondences and deformations. In our method, we

can see the cubiﬁction step as a template deformation,

where the template is the unit cube, and where the

deformation is not learned but computed. We try to

achieve similar results, in surface quality and inter-

polation smoothness, but without the constraints and

limitations of deep learning as explained above.

Parametric and Statistical Shapes Descriptors

Describing a shape class by a given set of param-

eters (also referred to as a dictionary) is a funda-

mental operation for applications such as classiﬁca-

tion, model retrieval, or similarity search. Some ap-

proaches (Kalogerakis et al., 2012; Haibin et al., 2015)

learn probabilistic distributions of shapes from the

properties of their semantical parts, or even from the

relations between parts simpliﬁed into simpler geo-

metric primitives (Tulsiani et al., 2017). Others learn

explicit parameterizations, typically possible on shapes

representing body poses (Allen et al., 2003).

Our method relies on shape cubiﬁction, serving as a

shape descriptor which, while being class-independent,

is more adapted to shapes having strong reﬂection sym-

metries. The key difference with these other methods

is twofold. First, we show how traversing the space of

plausible shapes does not require statistical inference

but can be expressed as a minimal-path problem in

a graph, whose structure captures the geometric rela-

tions between existing shapes. Second, our descriptor

is invertible, which allows us to generate new shapes

(for the intermediate states of morphings), without any

neural network.

r = 0 r = 1 r = 2 r = 3

Figure 1: Optimization of DVGs at progressive resolutions

(constant number of steps per r).

Deformable Voxel Grids

Our cubiﬁction relies on Deformable Voxel Grids

(Groscot, 2021; Groscot and Cohen, 2022), a model in-

spired by the Topological Active Volume (TAV) from

(Barreira et al., 2003), which is a volumetric exten-

sion of active contours (Kass et al., 1988; Cohen,

1991). The unfamiliar reader can think of active con-

tours as parametric curves which minimize a given

energy, typically used for segmenting objects in im-

ages (Hemalatha et al., 2018). In the case of DVGs, the

energy ensures that after an initialization as a regular

voxel grid around the input shape, the grid is optimized

until it tightly and smoothly embraces the shape (see

Figure 1).

3 INVERTIBLE CUBIFICTION

VIA DVGs

The purpose of cubiﬁction is to offer a consistent rep-

resentation basis for several shapes belonging to the

same class (e.g. chair or car): the same semantical

parts of different objects tend to occupy the same re-

gion of the cube, allowing for easier shape compar-

isons (see how we deﬁne a distance between cubiﬁed

shapes in Section 4). In order to do so, we optimize a

DVG and interpret it as a smooth deformation of the

unit cube

adapted to a given shape

, and apply the

inverse deformation to S.

3.1 Forward DVG Projection

For a given DVG cell

, a point

inside can be ex-

pressed by its local coordinates, a triplet in [0,1]

˜u, ˜v, ˜w ∈ [0,1]

s.t. f

( ˜u, ˜v, ˜w) = q (1)

where

, p

,..., p

are the positions of the eight

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

100

(a) Bilinear interpola-

tion

(b) DVG-voxel correspon-

dence

Figure 2: A natural way of setting grid coordinates on a

quadrilateral is via bilinear interpolation, which maps reg-

ular subdivisons of

[0,1]

onto the quad cell (left to right).

Determining the local coordinates of a given point within

the cell corresponds to inverting this interpolation (right to

left). The same is done for registering a point inside a DVG,

but in 3D, with the inversion of a trilinear interpolation.

vertices of

. The interpolator

can be linear or

smooth (we use, respectively, a trilinear

tri

and a Thin

Plate Spline

t ps

interpolators). Both can be deﬁned

by matching the control points

of a regular cube to

V , those of a given DVG.

Then, an afﬁne transformation maps the cell to its

correct location within the whole DVG grid system

(see Figure 2).

3.2 Backward DVG Projection

We suppose the signed distance ﬁeld (SDF) of shape

is given. Each cell of

is subdivided into smaller

subcells, and the value of the SDF is queried at the

locations of each subcell centroid, which naturally

have

(u,v,w)

coordinates, coming from the index-

ing of

: vertex index

(i, j,k)

has local coordinates

(u,v,w) = (

r−1

)

. The cubiﬁed SDF can be

used in two ways.

Shape Cubiﬁction and Reconstruction: Using

marching cubes (Lorensen and Cline, 1987), we obtain

, the mesh of the cubiﬁed shape, where the precision

of the geometry is limited by the grid resolution of the

DVG and the number of cell subdivisions. The original

shape can be recovered by projecting

into

using

the spline projector

t ps

. This operation is important

because it gives the baseline shape representation ca-

pacity for the morphings we generate: as a matter of

fact, our morphings are done in

-space and

-space

separately, and use the

t ps

projector to effectively cre-

ate the intermediate shapes. The intuition is that the

DVG separates style and conﬁguration, respectively

into

and

. This way, we ﬁnd morphings that min-

imize the amount of displaced mass to transfer style

(

), while the deformation abilities of the grid allow

to interpolate the conﬁgurations V .

Figure 4 shows examples of such cubiﬁctions and

reconstructions using both p

tri

and p

t ps

Content Descriptor: We can extract the volume in-

dicator function

by thresholding the SDF. Its av-

erage value is binned within each DVG cell, in order

to obtain an

voxel image which serves as a shape

content descriptor. Each cell value, between 0 and 1,

represents the proportion of the cell which intersects

the shape. This descriptor allows to regroup models by

similarity in order to build a shape graph, as explained

in the following Section.

4 GRAPH-BASED SHAPE SPACE

After all shapes of a dataset are consistently cubiﬁed,

we propose to discretize the global shape space in the

form of a weighted graph, whose edges derive from

a similarity measure between cubiﬁed shapes. This

graph formalizes the notion of shape morphing, as

a morphing from shape

will correspond to a

minimal path from node

. This choice is

motivated by the fact that for a large enough shape

dataset, most intermediate steps of a morphing are

close to existing shapes.

This is why we explore the possibility of discrete

morphings, restricted to known shapes, effectively

bypassing the necessity to learn how to sample new

shapes; while imposing them a minimal energy crite-

ria.

We ﬁrst present a general framework for shape

morphings as minimal paths in a shape graph, for any

arbitrary shape embedding. Then, we show how it can

be used with cubiﬁed shapes and how our invertible

cubiﬁction actually allows to easily extrapolate the

discrete morphings to continuous ones.

4.1 Morphings as Minimal Paths

In this part, we consider the problem of morphings

with shape priors, that is to say, morphings such that

intermediate states are plausible. We operate under

the minimal assumption that the shape prior is given

by a ﬁnite set of exemplars,

S = {S

,··· ,S

}

, where

the shapes are given in an arbitrary embedding. A

morphing corresponds to a sequence of shapes from

, but we want a metric to evaluate the quality of a

morphing. In order to do so, we impose a cost (or an

energy) to a morphing:

E(M = (S

,··· ,S

)) ≜

k−1

∑

i=1

E(S

i+1

) (2)

Where

E(S

)

is the energy of the transition

→

. Such energies can be evaluated as paths length in a

weighted graph G deﬁned by:

Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes

101

•

nodes

,··· ,N

}

, corresponding to the shapes

in S;

•

positive weighted edges

i, j

}

where

i j

can be

interpreted as a similarity between shapes

and

By convention, an absent edge

(i, j)

is equivalent

to w

i j

= ∞.

We call a morphing

A →B

minimal if it is achieved

by a shortest path in

from

. In order to

consider symmetric morphings (i.e. equal to the time-

reversed morphing), we assume

in an undirected

graph, i.e, ∀i, j,w

i, j

= w

j,i

4.2 Graph of Cubiﬁed Shapes

We can apply the previous formalism to the space of

cubiﬁed shapes. We propose a metric between shapes

cubiﬁed via a DVG (according to the method described

in Section 3), which interprets as an approximate trans-

port cost.

We ﬁrst compute the volumetric DVG descriptor

(see 3.2), where each cell of the DVG is attributed a

value between 0 and 1, corresponding to the proportion

of the cell which is occupied by the shape. This pro-

vides a voxel image of a cubiﬁed shape. With a DVG

resolution

r = 8

, this leads to a representation space

with

= 512

dimensions, enough for the curse of

dimensionality to prevent Euclidian distances from be-

ing meaningful. This naive approach does not leverage

the proximity of the cells, which is why we propose a

method based on the morphological dilation operator.

Atypical Models Detection and Removal

A preliminary step is to exclude models for which the

aforementioned volumetric descriptor is inadequate,

that is to say, when the density of presence inside the

cells is not homogeneous. To detect such models, we

simply compute and sum all the inner-cell standard

deviations of the discrete

obtained in Section 3.2.

Figure 3 shows the most adequate and inadequate mod-

els for the chair dataset: unsurprisingly, sofas and

armchairs, which admit blocky cubiﬁctions, are the

most adequate models; while chairs with many intri-

cate details are the least. Because our descriptor, and

the subsequent similarity metric, are blind to these er-

rors, removing these inadequate shapes from the graph

shape space prevents them from appearing in shape

morphings.

Similarity Metric

Using the cross structuring element, real-valued di-

lation allows to add a one-voxel margin to a shape.

Thus, the added voxels all correspond to cells whose

Adequate models Inadequate models

Figure 3: Examples of adequate and inadequate models, with

respect to our volumetric descriptor which averages density

of presence within 8 ×8 ×8 DVG cells.

distance to the shape is

. We can deﬁne a forward

similarity metric

from descriptor

, which

penalizes the mass of

located outside the dilation of

= min(dilation(A) −B, 0)

= min(dilation(B) −A, 0)

d(A, B) ≜ ∥D

∥

+ ∥D

∥

(3)

Note that for all locations outside of

dilation(A)

the penalty imposed by

∥D

∥

is the same as the

voxel distance. Thus, for dissimilar models (e.g., if

is mostly located outside of

dilation(A)

), this metric

becomes less interpretable, because of the curse of

dimensionality. We use this metric to build a shape

graph

, after all pairwise distances are evaluated.

In general, each shape is connected to its k-nearest

neighbors. However, the linking rules can vary for

several reasons:

•

Certain shapes may be particularly different from

the rest of the dataset. In order to prevent them

from being considered in morphings, we trim off

links whose weights are above a threshold τ

•

To ensure that the ﬁnal graph

is made of only

one connected component, we can also decide to

keep at least

min

connections for every node, even

if their weights are above τ

The impact of such trade-offs is discussed in Sec-

tion 6.3.

4.3 Continuous Morphings

To ﬁnd a minimal path in

, we use Dijkstra’s algo-

rithm. The returned length corresponds to the energy

of the minimal morphing, while the sequence of nodes

provides a discrete morphing. Thanks to our invertible

cubiﬁction, this shape sequence can be prolonged to a

continuous morphing, by interpolating separately the

style and content

(V,C)

of each shape. For the control

points positions

, the interpolation is trivial and can

just be linear; as for the interpolation of content values,

we also propose linear interpolation. More precisely,

we interpolate the cubiﬁed SDFs, and generate the

geometry with marching cubes.

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

102

Because each edge in the path has a known length,

the continuous path can be parameterized by arc length

(see Discussion 6.6). For an arbitrary number of

frames, whose positions are equally spaced along the

path, this grants more interpolation frames in between

less similar shapes, which are the most likely to have

topology changes.

For a given sequence of style-content separated

shapes (

)

, ...,

)

), and their corresponding

edge lengths

L = (l

, ...,

k−1

)

, we can formalize

the continuous morphing using a time parameter

t ∈

[0,1]:

i,i + 1,

t = s

(t)

V = (1 −t) ·V

+t ·V

y(t) = p

tps

((1 −

t) ·C

t ·C

i+1

)

(4)

Where

(t)

is the discrete arc lenth parameteri-

zation function, returning the indices

(i,i + 1)

of the

edge nodes and the local time parameter

. Note that

the interpolation on

is straight from

: the

graph G is only used for interpolating the content C.

The same framework can be used to morph be-

tween new, unknown shapes, by embedding them into

graph

, following all the steps: DVG optimization,

shape cubiﬁction, links creation to connect these new

shapes to the already-existing graph.

5 RESULTS

We conducted our experiments using shapes from the

ShapeNet (Chang et al., 2015) dataset; more speciﬁ-

cally using 500 from the chair category and 200 from

the car category. Because the continuous morphings

require all shapes to be closed manifolds, and for fair

comparisons against (Kleineberg et al., 2020) which

preprocesses shapes the same way, we ﬁrst converted

them into manifolds using the same method as (Park

et al., 2019). We then sampled

l = 4096

points to be

used as the DVG input pointclouds.

5.1 Shape Morphings

To produce shape morphings, we randomly picked

pairs of nodes in

, and applied the method explained

in Section 4.3. Following Equation

(4)

, each morphing

consists in a sequence of triplets

(

V ,

C, y)

. While we

are typically only interested in the ﬁnal geometry

observing

and

provides, along with the found

minimal path in

, an explanation for the generated

geometries. We show such triplets in Figure 5.

5.2 Robustness to Misalignment

We assume all our shapes are consistently aligned,

as standard among generative models. However, be-

ing a deformable model, we tested the ability of the

DVG to converge to the correct conﬁguration when

the input shape has been rotated. Given the hierarchi-

cal subdivisions and the centrality of the ﬁrst levels

(see discussion in Section 6), we compared the de-

termined ﬁrst level for two conditions: ground truth

alignment, and noisy alignment (rotation with random

Euler angles, according to

N (0, σ = 0.2rad ≈ 12

◦

)

For fairness, we kept a constant number of gradient

descent steps. The error is then measured as the Eu-

clidean distance between the control points of the two

grids,

∥GT −pred∥

. Figure 6 shows an example of a

misaligned grid

We also estimated, for any given

max

≤τ

(∥GT −pred∥

)

, the empirical expectancy on

datasets where the maximum angular error is smaller

than a threshold

(see plot in Figure 6). We observe

that it increases at a reasonably low pace, conﬁrming

the advantages of a deformable model. As for high

angular errors (more than

◦

), the predicted grid can

be ﬂipped: a control point which should be at the top

is now located on the side. For a single shape, this

is not a problem. However, on a whole dataset, this

would break the consistent cubiﬁction we require to

build our similarity measure.

5.3 Qualitative Analysis: Comparison

with Deep Learning

In our work, one of the main objectives was to produce

results comparable in quality to those obtained via

deep learning. We chose to compare our results to the

adversarial neural network developed by (Kleineberg

et al., 2020), as it also relies on an SDF representation,

and has published the weights of a pre-trained network,

allowing us to produce new morphings.

For fair comparisons, we adopted the following

methodology:

•

We kept our graph

untouched, built from the

same 500 chair examples as in the previous experi-

ments;

•

We ﬁrst generated baseline morphings as latent

space interpolations between random codes corre-

sponding to chairs (about 4k examples);

•

For each of these morphings, we extracted the ﬁrst

and last states: these provided query shapes that

we embedded in

(as explained in Section 4.3) in

order to generate our morphings;

Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes

103

Input

DVG VCube C

tri

(C)p

tps

(C)

Figure 4: (Zoom in to see details) Qualitative results for shape reconstruction via DVGs: estimating

for each shape allows to

cubify it (

), and this can be reprojected into

by a trilinear

tri

or a spline

tps

projector (see 3.1), the latter yielding smoother

surfaces. The cubiﬁed shapes are color-coded by assigning a value in [0,1]

to an RGB color.

•

To match the surface quality of (Kleineberg et al.,

2020), we decreased the resolution of our SDFs be-

fore the mesh reconstruction via marching cubes.

Figure 7 presents some comparative results, se-

lected for their representativity. Here are our observa-

tions for each of the ﬁve shown examples:

These shapes happened to have a direct link when

embedded in

: the morphing entirely comes from

the DVG.

While the morphing of the seat is visually pleasing,

the SDF interpolation is responsible for a hole in

the leg (frames 4–10).

The armrests removal looks less pleasing, but on

the ﬂip side, the progressive rounding of the back

is more natural.

Most of the artifacts (frames 7–12) come from the

short-circuit effect, discussed in 6.5.

Apart from similar surface artifacts, it exempli-

ﬁes the impact of our minimal paths for chair-to-

armchair morphings. Indeed, they appear to fa-

vor transitions which add thin armrests halfway

through.

When watched as videos, our morphings also ap-

pear generally less smooth. This is due to our SDF

interpolations: when new mass appears within the 1-

voxel margin, it can look sudden, and then less pleasant

to the eye. Despite these imperfections, we found it

pretty remarkable to achieve such results while only

relying on a much smaller dataset. It would indeed

seem hard, if not impossible, to train a neural network

with such limited data.

6 DISCUSSION

Our overall method comprises many components, each

requiring design choices which inﬂuence the quality

of the results. Because the systematic analysis of gen-

eral shape morphing (for non-parametric shapes) is

still uncharted territory, we presented quantitative and

qualitative results where each component is designed

in the minimally-viable way. However, our system

admits many local improvements.

Hence the following observations and suggestions,

noted from our experiments.

6.1

Importance of the First Hierarchical

Levels

While (Groscot and Cohen, 2022) establishes the im-

portance of the progressive reﬁnement of DVGs, our

experiments further emphasize the greater importance

of the ﬁrst levels. If the second level is unfrozen before

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

104

1a 2a

1b 2b

1c 2c

3a 4a

3b 4b

3c 4c

t 0 3 6 9 12 15 t 0 3 6 9 12 15

Figure 5: (Zoom in to see details) Examples of morphings generated with our method. Rows

(a)

(b)

, and

(c)

respectively

correspond to the interpolation of cubes C, ﬁnal shapes, and DVG grids V .

the ﬁrst level has correctly converged, the misalign-

ment of the cube edge with the dominant features of

the shape will remain. This problem can arise when

optimizing a batch of DVGs on many shapes, with a

constant number of epochs per level. To prevent this

from happening, one has to make sure the ﬁrst level

has enough time to converge on all the training shapes,

or resort to an adaptive gradient descent scheme.

6.2 Manual Edition of a DVG

In a real use case scenario, a determined DVG can

be manually corrected. For instance, it can easily be

symmetrized – by averaging with its symmetric. This

could be useful for shape reconstructions and mor-

phings, to ensure that the generated geometries are

indeed symmetric. All the results we show did not

resort to any manual correction, in order to exhibit the

bare abilities of our model. Yet it would be interesting,

for future work, to investigate the usefulness of ad-hoc

post-processing.

6.3 Graph Connectivity

The quality of the morphings generated by our method

depends on the graph building procedure, and more

speciﬁcally, the node linking rule. Ordinarily, these

graphs can be built obeying either a k-nearest neighbor

condition, or a distance threshold condition. By design,

our metric becomes less interpretable as the estimated

distance increases. This is why we need to impose a

distance threshold criteria. Doing so, the graph can

however have several connected components, limiting

the ability to interpolate between shapes of distinct

modes (say, between an ofﬁce chair and a sofa).

In practice, ﬁnding threshold values can be hard,

given the non-uniform distribution of pairwise dis-

tances (for instance, we observed that the distances

Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes

105

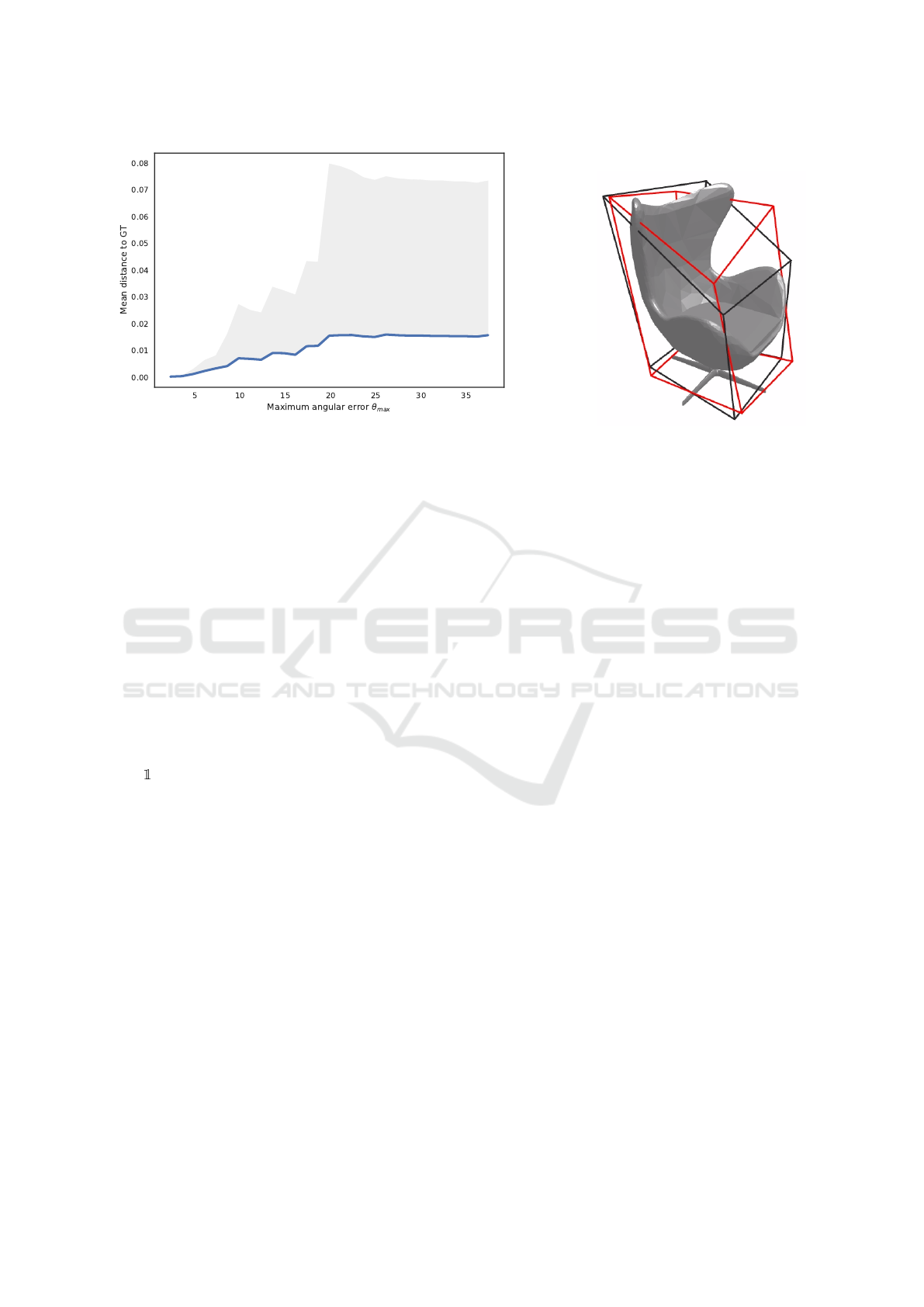
(a) Prediction error against shape misalignment (b) Misaligned v

Figure 6: (a) Mean error against maximum rotation angle θ

max

, grey area is the standard deviation; (b) Ground truth in black,

misaligned prediction in red, where θ

max

≈ 20

◦

, error = 0.078. Refer to Section 5.2 for a discussion on these ﬁgures.

between many sofas are disproportionately small). To

mitigate the potential mistakes, we build the k-nearest

neighbor graph with three constraints, in decreasing

priority: for node i,

1. k

≥ k

min

2. k

≤ k

max

3. ∀j ↔ i,d(S

) ≤ τ

6.4 Volumetric Descriptor Sensitivity

and Speciﬁcity

In order to preserve ﬁne information in the volumetric

descriptor, we decided to average the indicator func-

tion

within each DVG cell, instead of keeping all

cells where it is non null (which would correspond to

a classical voxelization). However, the values can be

small, and have a negligible inﬂuence on the similar-

ity measure, even where there is non-negligible mass.

Take the example of a half cube within a DVG cell, its

average presence density is

/8 = 0.125

. This is

why we propose to apply the cubic root as a contrast

function to increase sensitivity to low values – before

feeding the descriptors to the similarity metric

d(A, B)

We also performed experiments where the resolu-

tion of the volumetric descriptor is

r = 16

, effectively

halving the one-voxel margin tolerance. With this in-

creased speciﬁcity, neighbors are more similar than

before; but dissimilar models are further away than be-

fore. This led to discrete morphings which all contain

many intermediate steps. Overall, the generated mor-

phings were unpleasantly convoluted. We then settled

for

r = 8

as it appeared to be the best compromise, on

our chair dataset.

6.5 Misleadingly Low Similarity and

Short Circuits

Models whose topology is not adequately represented

by our metric are, as explained in Section 4.2, not

included in the graph. More precisely, we exclude the

20% most inadequate models.

But some models, not excluded from previous con-

siderations, can badly inﬂuence the quality of mor-

phings: those which display sharp surface features,

not captured by our descriptor. They are typically not

amongst the most adequate models, but still passed

the aforementioned 20% threshold. Such a situation is

depicted in Figure 7, rows (a).

Another interesting phenomenon appears when a

pair of unwanted models hijacks many morphings. If

they are each connected to distinct regions of

, they

provide a short circuit to many minimal paths.

This is the case for models at locations (1a,11)

and (1a,12). They indeed appeared in many of our

randomly generated morphings, creating unwanted

surface artifacts. We show, in rows (b), that manually

discarding these undesired models and short circuits

can enhance the quality of the outputs. However, we

kept all the other morphings we show in this paper

untouched, in order to exhibit the results without any

manual intervention.

6.6 Metric and Arc-Length

Parameterization

Because our similarity measure

d(A, B)

only penalizes

difference in shapes beyond a one-voxel margin, many

pairs of shapes have a low distance, sometimes even

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

106

t 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Figure 7: (Zoom in to see details) Manual intervention on morphings: some generated morphings can display unsightly

intermediate shapes because of the found minimal path (see

(a)

rows, at times 10 through 12). Manually discarding the

unwanted models from the graph allows to redetermine an alternative, more pleasing, morphing ((b) rows).

null. This is due to the fact that the dataset contains

many redundant shapes, with similar content

(for

instance, many chairs resembling the model on Fig-

ure 7 at (1a,0). Contrary to the previous discussion 6.5

(on misleadingly low similarity), this is the case where

similarities ought to be low. Conversely, for dissimilar

shapes, the edge length can be disproportionately large,

accounting for most of the total path length.

Since the discrete paths make continuous morph-

ings by arc-length parameterization, this issue can lead

to unpleasing morphings. It could have ben addressed

in two ways:

Regrouping, like (Gao et al., 2013), cliques of

interconnected shapes; and allowing at most one

representative of a clique within a morphing;

Applying a non-linear transformation on the path

length, before the generation of the continuous

morphing.

We opted for the second option as it is the simplest

and provides the baseline we are aiming for. We apply

the function

x 7→ 1 +

√

, where the square root rebal-

ances low and high values, and the constant 1 corrects

for the almost-null edge lengths.

7 CONCLUSION

The idea presented in this paper is, essentially, to con-

nect shapes similar in content, so that morphing be-

tween them is “simple”: the DVG cubiﬁction trick

makes such a simple formulation of morphings pos-

sible. As we have shown, performing a simple linear

interpolation on cubiﬁed SDFs already generates qual-

itatively pleasing morphings, therefore establishing a

strong baseline. More complex approaches, based for

instance on optimal-transport, could probably yield

better results. Yet, we produced results qualitatively

similar to the state-of-the-art deep learning methods,

while relying on limited data.

Even if our DVG shape parameterization is not spe-

ciﬁc to any class, we restricted our analysis to chairs,

because of the challenges posed by their varied topolo-

gies, and also showed initial results on cars. Moreover,

their strong reﬂection symmetries are compatible with

cubiﬁction.

For future work, we would like to investigate the

use of this model on shape categories displaying less

symmetries. It would also be interesting to reproduce

these results at a larger scale, say with the complete

chair subset of ShapeNet, or even when adding other

categories to the same graph: would we ﬁnd different

shape types separated in different clusters?

Finally, we could bridge the gap between our

method and neural networks. Indeed, the SDFs in-

terpolations are inherently limited and may not be able

to fully capture shape priors, even in a large scale ap-

plication. In this case, a generative model, trained

only on cubiﬁed shapes for instance, could provide an

interesting solution.

ACKNOWLEDGEMENTS

This work was funded in part by the French govern-

ment under management of Agence Nationale de la

Recherche as part of the “Investissements d’avenir”

program, reference ANR-19-P3IA-0001 (PRAIRIE

3IA Institute).

Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes

107

REFERENCES

Achlioptas, P., Diamanti, O., Mitliagkas, I., and Guibas,

L. J. (2017). Learning representations and generative

models for 3D point clouds.

Allen, B., Curless, B., Curless, B., and Popovi

c, Z. (2003).

The space of human body shapes: Reconstruction

and parameterization from range scans. ACM Trans.

Graph., 22(3):587–594.

Barreira, N., Penedo, M. G., Mari

no, C., and Ansia, F. M.

(2003). Topological active volumes. In Petkov, N. and

Westenberg, M. A., editors, Computer Analysis of Im-

ages and Patterns, pages 337–344, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Chang, A. X., Funkhouser, T., Guibas, L., Hanrahan, P.,

Huang, Q., Li, Z., Savarese, S., Savva, M., Song, S.,

Su, H., Xiao, J., Yi, L., and Yu, F. (2015). ShapeNet:

An Information-Rich 3D Model Repository. Technical

Report arXiv:1512.03012 [cs.GR], Stanford Univer-

sity — Princeton University — Toyota Technological

Institute at Chicago.

Cohen, L. D. (1991). On active contour models and balloons.

CVGIP: Image Understanding, 53(2):211 – 218.

Dubrovina, A., Xia, F., Achlioptas, P., Shalah, M., Groscot,

R., and Guibas, L. J. (2019). Composite shape model-

ing via latent space factorization. In The IEEE Interna-

tional Conference on Computer Vision (ICCV).

Fan, H., Su, H., and Guibas, L. J. (2016). A point set

generation network for 3D object reconstruction from

a single image. CoRR, abs/1612.00603.

Fish, N., Averkiou, M., van Kaick, O., Sorkine-Hornung,

O., Cohen-Or, D., and Mitra, N. J. (2014). Meta-

representation of shape families. ACM Trans. Graph.,

33(4):34:1–34:11.

Gao, L., Lai, Y.-K., Huang, Q., and Hu, S. (2013). A data-

driven approach to realistic shape morphing. Computer

Graphics Forum, 32.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Bengio,

Y. (2014). Generative adversarial networks.

Groscot, R. (2021). Separable 3D Shape Representations

for Shape Processing. PhD thesis. Th

ese de doctorat

dirig

ee par Cohen, Laurent David Math

ematiques ap-

pliqu

ees Universit

e Paris sciences et lettres 2021.

Groscot, R., Cohen, L., and Guibas, L. (2019). Shape part

transfer via semantic latent space factorization. In

Nielsen, F. and Barbaresco, F., editors, Geometric Sci-

ence of Information, pages 511–519, Cham. Springer

International Publishing.

Groscot, R. and Cohen, L. D. (2022). Deformable voxel

grids for shape comparisons. In Jiang, X., Tao, W.,

Zeng, D., and Xie, Y., editors, Fourteenth International

Conference on Digital Image Processing (ICDIP 2022),

volume 12342, page 123423G. International Society

for Optics and Photonics, SPIE.

Groueix, T., Fisher, M., Kim, V. G., Russell, B., and Aubry,

M. (2018). AtlasNet: A Papier-M

ach

e Approach to

Learning 3D Surface Generation. In CVPR 2018, Salt

Lake City, United States.

Haibin, H., Kalogerakis, E., and Marlin, B. (2015). Analysis

and synthesis of 3D shape families via deep-learned

generative models of surfaces. Computer Graphics

Forum, 34.

Hanocka, R., Fish, N., Wang, Z., Giryes, R., Fleishman,

S., and Cohen-Or, D. (2018). Alignet: Partial-shape

agnostic alignment via unsupervised learning.

Hao, Z., Averbuch-Elor, H., Snavely, N., and Belongie, S.

(2020). Dualsdf: Semantic shape manipulation us-

ing a two-level representation. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition (CVPR).

Hemalatha, R., Thamizhvani, T., Dhivya, A. J. A., Joseph,

J. E., Babu, B., and Chandrasekaran, R. (2018). Active

contour based segmentation techniques for medical

image analysis. In Koprowski, R., editor, Medical

and Biological Image Analysis, chapter 2. IntechOpen,

Rijeka.

Kalogerakis, E., Chaudhuri, S., Koller, D., and Koltun, V.

(2012). A probabilistic model for component-based

shape synthesis. ACM Trans. Graph., 31(4):55:1–

55:11.

Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:

Active contour models. International Journal of Com-

puter Vision, 1(4):321–331.

Kingma, D. P. and Welling, M. (2013). Auto-Encoding Vari-

ational Bayes. arXiv e-prints, page arXiv:1312.6114.

Kleineberg, M., Fey, M., and Weichert, F. (2020). Adversar-

ial generation of continuous implicit shape representa-

tions.

Kurenkov, A., Ji, J., Garg, A., Mehta, V., Gwak, J., Choy,

C., and Savarese, S. (2017). Deformnet: Free-form

deformation network for 3d shape reconstruction from

a single image.

Li, J., Xu, K., Chaudhuri, S., Yumer, E., Zhang, H., and

Guibas, L. J. (2017). GRASS: Generative recursive

autoencoders for shape structures. ACM Transactions

on Graphics (Proceedings of SIGGRAPH 2017).

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3d surface construction algorithm.

SIGGRAPH ’87, New York, NY, USA.

Niemeyer, M., Mescheder, L., Oechsle, M., and Geiger, A.

(2019). Occupancy ﬂow: 4d reconstruction by learning

particle dynamics. In International Conference on

Computer Vision.

Park, E., Yang, J., Yumer, E., Ceylan, D., and Berg, A. C.

(2017). Transformation-grounded image generation

network for novel 3d view synthesis. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition (CVPR).

Park, J. J., Florence, P., Straub, J., Newcombe, R., and Love-

grove, S. (2019). Deepsdf: Learning continuous signed

distance functions for shape representation. In Proceed-

ings of the IEEE/CVF Conference on Computer Vision

and Pattern Recognition (CVPR).

Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2016). Pointnet:

Deep learning on point sets for 3D classiﬁcation and

segmentation.

Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017). Pointnet++:

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

108

Deep hierarchical feature learning on point sets in a

metric space. CoRR, abs/1706.02413.

Sederberg, T. W. and Parry, S. R. (1986). Free-form deforma-

tion of solid geometric models. SIGGRAPH Comput.

Graph., 20(4):151–160.

Shin, D., Fowlkes, C. C., and Hoiem, D. (2018). Pixels,

voxels, and views: A study of shape representations

for single view 3d object shape prediction. In 2018

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 3061–3069.

Tatarchenko, M., Dosovitskiy, A., and Brox, T. (2017). Oc-

tree generating networks: Efﬁcient convolutional ar-

chitectures for high-resolution 3D outputs. CoRR,

abs/1703.09438.

Tulsiani, S., Su, H., Guibas, L. J., Efros, A. A., and Malik,

J. (2017). Learning shape abstractions by assembling

volumetric primitives. In Computer Vision and Pattern

Regognition (CVPR).

Wang, N., Zhang, Y., Li, Z., Fu, Y., Liu, W., and Jiang, Y.-G.

(2018). Pixel2mesh: Generating 3d mesh models from

single rgb images. In ECCV.

Wu, J., Zhang, C., Xue, T., Freeman, W. T., and Tenenbaum,

J. B. (2016). Learning a probabilistic latent space of

object shapes via 3D generative-adversarial modeling.

In Proceedings of the 30th International Conference

on Neural Information Processing Systems, NIPS’16,

pages 82–90, USA. Curran Associates Inc.

Zheng, Z., Yu, T., Dai, Q., and Liu, Y. (2020). Deep implicit

templates for 3d shape representation.

Shape Morphing as a Minimal Path in the Graph of Cubiﬁed Shapes

109