Assessment of Digital and Mathematical Problem-Solving

Competences Development

Alice Barana

, Cecilia Fissore

, Anna Lepre

and Marina Marchisio

Department of Foreign Languages, Literatures and Modern Culture, Via Giuseppe Verdi Fronte 41, 10124 Turin, Italy

Department of Molecular Biotechnology and Health Sciences, University of Turin, Via Nizza 52, 10126, Turin, Italy

Keywords: Advanced Computing Environment, Digital Competences, Problem Solving, Problem-Solving Skills.

Abstract: Problem-solving and digital competences assume an essential role in developing students' life-long learning

competences. An effective tool to support problem-solving activities is an Advanced Computing Environment

(ACE). An ACE is a system that allows to perform numerical and symbolic calculation, make graphical

representations, and create mathematical simulations through interactive components. Moreover, it is able to

support students in reasoning processes, in the formulation of exit strategies and in the generalization of the

solution. The main goal of this paper is to study the development of problem-solving and digital competences

of secondary school students solving problems with an ACE in a Digital Learning Environment (DLE). The

research question is: "How can we evaluate the evolution of students' problem solving and digital competences

during the online training?”. To answer the research question, the resolutions of 158 grade 12 students to ten

problems carried out during an online training were analyzed. The research methodology was divided into

three phases: the analysis of a case study; the analysis of all student evaluations; the analysis of students'

answers to a final questionnaire. The results show that solving contextualized problems with the ACE in a

DLE enhanced the students' problem-solving and digital competences.

1 INTRODUCTION

Every individual needs to develop skills that can be

used throughout their lives: to respond to the

challenges of a world in which technologies influence

society, teaching and education, to improve as a

person and as a worker, and to be an active citizen. In

the recommendations relating to the key competences

for lifelong learning, the Council of the European

Union includes the problem-solving competence and

the digital competence (European Parliament and

Council, 2018). According to the European

Parliament and Council (2018): "Competences, such

as problem solving, critical thinking, ability to

cooperate, creativity, computational thinking, self-

regulation are more essential than ever before in our

quickly changing society. They are the tools to make

what has been learned work in real time, in order to

generate new ideas, new theories, new products, and

new knowledge". The Digital competence involves

https://orcid.org/0000-0001-9947-5580

https://orcid.org/0000-0001-8398-265X

https://orcid.org/0000-0002-1332-2442

https://orcid.org/0000-0003-1007-5404

the confident, critical and responsible use of, and

engagement with, digital technologies for learning, at

work, and for participation in society. These aspects

are also mentioned in the Italian National Guidelines

(MIUR, 2010), according to which students at the end

of upper secondary school should be able to apply

mathematical concepts to solve problems, also with

the help of technologies. Therefore, proposing

problem-solving activities with the use of digital

technologies is a teaching methodology that responds

to institutional objectives.

This research work has the main goal of

evaluating the development of problem-solving and

digital competences of secondary school students

who carry out problem-solving activities with an

Advanced Computing Environment (ACE), during an

online training in a Digital Learning Environment

(DLE). An ACE, with a special programming

language, allows for performing numerical and

symbolic computations, plotting two- and three-

318

Barana, A., Fissore, C., Lepre, A. and Marchisio, M.

Assessment of Digital and Mathematical Problem-Solving Competences Development.

DOI: 10.5220/0011987800003470

In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023) - Volume 2, pages 318-329

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

dimensional static or dynamic graphs and

programming interactive components in order to

generalize a resolution process. An ACE also allows

students to approach a problematic situation in the

way that best suits their thinking, to use different

types of representations according to the chosen

strategy and to display the whole reasoning together

with verbal explanation in the same page (Barana et

al., 2019). All of this makes it an effective tool to

support problem solving and mathematics teaching

and learning (Brancaccio et al., 2015; Barana et al.,

2021). A DLE has been defined as an ecosystem in

which teaching, learning, and the development of

competence are fostered in classroom-based, online

or blended settings. It is made up of a human

component, a technological component, and the

interrelations between the two (Barana & Marchisio,

2022). According to Suhonen (2005), a DLE is a

“technical solution for supporting learning, teaching

and studying activities”.

The context of our research is the Digital Math

Training (DMT) project funded by the Fondazione

CRT within the Diderot Project and organized by the

Delta Research Group of the University of Turin in

Italy. The DMT project every year involves about

3000 upper secondary school Italian students. The

main goal of the project is to allow students to

develop digital and problem-solving competences by

solving contextualized problems with an ACE and

collaborating with each other remotely within an

integrated DLE (available at the link:

https://digitalmatetraining.i-learn.unito.it/) (Barana

& Marchisio, 2016; Barana, Boetti & Marchisio,

2022).

This study is guided by the following research

question: "How can we evaluate the evolution of

students' problem-solving and digital competences

during the online training?”. To answer the research

question, the course of the 12

grade students of the

DMT edition of the 2021/2022 school year was

analyzed. The submissions and all data relating to the

assessments obtained by 158 students during the

online training were collected and analyzed. The

students' answers to the final questionnaire that they

filled out at the end of the online training were also

analyzed.

This paper is structured as follows. In the section

“Theoretical framework” the methodology of

problem solving and problem solving with an ACE

are discussed, followed by a brief presentation of the

DMT project. In the section "Methodology" the

research methodology with which the analysis was

carried out is presented. The main results obtained

from the analyses are presented in the "Results"

section. In the "Conclusions" section some reflections

on the results obtained and possible further

developments for the research are presented.

2 THEORETICAL FRAMEWORK

2.1 Problem Solving and Problem

Solving with an ACE

One of the fundamental skills in Mathematics is the

ability to solve problems in everyday situations,

which includes the ability to understand the problem,

devise a mathematical model, develop the solving

process and interpret the obtained solution (Samo et

al., 2017). The term “problem solving” refers to

mathematical tasks which provide intellectual

challenges that improve students’ understanding and

mathematical development (National Council of

Teachers of Mathematics, 2000). Problem solving is

a real challenge for students. It involves the use of

multiple rules, notions and operations whose choice

is a strategic and creative act of the students

(D'Amore & Pinilla, 2006). Its value lies not only in

being able to find the final solution but also in

developing ideas, strategies, skills and attitudes. The

focus then shifts from the final solution to the

problem-solving process. Solving problems that are

contextualized in everyday life activates modeling

skills in students and teaches them to recognize how

and when to use their knowledge, as well as getting

them accustomed to solving problems in real world

situations (Baroni & Bonotto, 2015; Samo et al.,

2017). Challenging problems should be used, whose

content topics have been studied in class or will soon

be, with open data in order to offer students a vast

range of possibilities to choose from and make

decisions about, and that suggest more than one

solving strategy (Barana et al., 2022). Through

problem solving it is also possible to develop social

and civic competences. For example, by solving

problems in small groups, students learn to work

together, to discuss, to support their own opinions and

respect those of others, to discuss and present their

ideas. Therefore, by learning problem solving in

Mathematics, students acquire ways of thinking,

creativity, curiosity, collaborative competences and

confidence in unfamiliar situations (Barana et al.,

2019).

The resolution of a problem by students can be

used to assess progress in problem-solving

competences, using an assessment rubric with a score

scale (Leong & Janjaruporn, 2015). The score scale

describes the reason why a performance was placed

Assessment of Digital and Mathematical Problem-Solving Competences Development

319

in a certain level. The next level guidance provides

students with an idea of what should be achieved and

what needs to be done to improve. The rubric is one

of the best ways to assess problem-solving

competence (Jonassen, 2014). It can be used to

evaluate problems on different mathematical topics

and the evaluations can be compared. Moreover,

through rubric assessment, students are provided with

relevant feedback on the problem-solving process,

since they receive an evaluation on each indicator

(Jonassen, 2014). Sharing rubrics with detailed

descriptors of the levels is a relevant formative

assessment strategy, since it helps students

understand the quality criteria (Black & Wiliam,

2009). In fact, through rubric assessment they can

understand their actual level, the reference level, and

in which area they should work more to reach the

goals: these are the three main processes of formative

assessment identified by Black and Wiliam (2009)

and by Hattie and Timperley (2007). Thus, feedback

provided through rubrics can help them bridge the

gap between current and desired performance in

problem solving (Hattie & Timperley, 2007).

Problem solving is characterized by four

fundamental phases described by Polya (1945) in

"How to solve it": understanding the problem,

devising a plan, carrying out the plan, looking back.

The looking back phase consists of reviewing and

reconsidering the results obtained and the process that

led to them. This allows one to consolidate

knowledge, better understand the solution and

possibly use the result, or the method, for some other

problem. Generalizing is an important process by

which the specifics of a solution are examined and

questions as to why it worked are investigated

(Liljedahl et al., 2016). This process can be compared

to the Polya looking back phase, and consists of a

verification and elaboration stages of invention and

creativity. This makes it possible to move from the

single case to all possible cases, to extend and readapt

the model developed and to consolidate what has

been learned through problem solving (Malara,

2012).

Technologies play a fundamental role in problem

solving and make it possible to amplify all phases of

the process. An ACE allows to perform numerical and

symbolic computations, make graphical

representations (static and animated) in 2 and 3

dimensions, create mathematical simulations, write

procedures in a simple language, programming, and

finally elegantly connect all the different

representation registers also with verbal language in

a single worksheet (Barana et al., 2020). An important

aspect of an ACE for problem solving is the design

and programming of interactive components (such as

sliders, buttons, checkboxes, text areas, tables and

graphics). They enable to visualize how the results

change when the input parameters are changed and

thus they allow to generalize the solving process of a

problem. The use of an ACE for problem solving

profoundly affects the entire problem-solving

practice and the nature of the problems that can be

posed. For example, problems may require difficult

pen-and-paper calculations, dynamic explorations,

algorithmic solutions to approximate results, and

much more. Without having to engage in calculations,

students can focus on understanding, exploring and

discussing the solving process and the obtained

results. The possibility of combining different types

of representation in the same worksheet influences

the way students approach problems and their

strategic choices, favoring high levels of clarity and

understanding (Barana et al., 2022). In this way, the

ACE is not only a tool, but it becomes an effective

methodology that can support problem solving and

the learning of Mathematics (Fissore et al., 2019).

Another technology that can enhance the

problem-solving methodology is a Digital Learning

Environment, i.e., an ecosystem in which teachers

and students can share resources and carry out

educational activities. In a DLE both the

technological component and the human component

are important, together with how the activities are

designed for the interactions between students,

teachers and peers. In a DLE, teachers can propose

many different types of activities in a single shared

environment; this aspect is essential in an online

teaching context, but it can also integrate the teaching

experience into ordinary teaching in classroom-based

or in a blended mode. In a DLE students can create,

share and compare their own works and always be in

contact with each other, exchanging opinions and

ideas (Barana & Marchisio, 2022).

2.2 The Digital Math Training Project

The DMT Project was funded by the Fondazione

CRT within the Diderot Project and was organized by

the University of Turin. The DMT was born in 2014

with the aim of developing and strengthening the

mathematical, digital and problem-solving

competences of secondary school students. The main

part of the project consists of an online training in a

DLE. The technological component of the DLE is a

Moodle platform integrated with the Maple ACE

(https://www.maplesoft.com/), developed by the

Computer Science Department of the University of

Turin. The activities of the DMT project are mainly

CSEDU 2023 - 15th International Conference on Computer Supported Education

320

based on the resolution, with the use of an ACE, of

non-routine problems, contextualized in reality and

open to different solving strategies. Students solve the

problem individually, collaborating asynchronously

online with other students. Students are also offered

training activities and tools that enable self-learning

and collaborative learning to understand how to use

an ACE and solve problems. Students from grade 9 to

grade 13 participate in the project. The students are

divided by grade, then five online training sessions

are designed and set up on the platform. During the

online training, a problem is proposed to the students

every ten days, for a total of 8 problems. The degree

of difficulty of the problems gradually increases

during the training. Increasing the difficulty of the

problems allows students to prepare for a final

competition and win a prize. All problems include

several requests. The first requests guide students to

understand, explore, identify a model and the solution

strategy of the problematic situation. The last

problem request requires a generalization of the

solution through the creation of interactive

components.

The problems’ solutions worked out by the

students are assessed by tutors according to a rubric

designed to evaluate the competences in problem-

solving while using an ACE. The rubric is an

adaptation of the one proposed by the Italian Ministry

of Education to assess the national written exam in

Mathematics at the end of Scientific Lyceum,

developed by experts in pedagogy and assessment.

The rubric has 5 indicators, each of which can be

graded with a level from 1 to 4. The first four

indicators have been drawn from Polya’s model and

refer to the four phases of problem solving; they are

the same included in the ministerial rubric. The

project’s adaptation mainly involves the fifth

indicator, and entails the use of the ACE, which we

chose to separate from the other indicators in order to

have and be able to provide students with precise

information about how the ACE was used to solve the

problem. Since the objective of the project is

developing problem solving with technologies, it has

been considered appropriate to evaluate the

improvements also in the use of the ACE in relation

to the problem to solve (Barana et al., 2022). The five

indicators are the following:

 Comprehension: Analyze the problematic

situation, represent, and interpret the data and

then turn them into mathematical language

(score between 0 and 18);

 Identification of a solving strategy: Employ

solving strategies by modeling the problem and

by using the most suitable strategy (score

between 0 and 21);

 Development of the solving process: Solve the

problematic situation consistently, completely,

and correctly by applying mathematical rules

and by performing the necessary calculations

(score between 0 and 21);

 Argumentation: Explain and comment on the

chosen strategy, the key steps of the building

process and the consistency of the results (score

between 0 and 15);

 Use of an ACE: Use the ACE commands

appropriately and effectively in order to solve

the problem (score between 0 and 25).

A total score (maximum of 100) is given to each

resolution. Finally, each evaluation is integrated with

personalized feedback from the tutors, relating to the

evaluation obtained and containing advice on how

and what to improve. At the end of the training, all

participants are asked to fill out a satisfaction

questionnaire.

3 METHODOLOGY

The research question is: "How can we evaluate the

evolution of students' problem-solving and digital

competences during the online training?”. To answer

the research question, the course of the 12th grade

students of the DMT edition of the 2021/2022 school

year was analyzed. The submissions and all data

relating to the assessments obtained by 158 students

during the online training were collected and

analysed. The analysis was divided into three phases:

the analysis of how digital and problem-solving

competences vary in an exemplary case study; the

analysis of all student evaluations from the beginning

to the end of the online training; the analysis of the

students' answers to the final questionnaire. The

average number of submissions was 92 in the first

half of the training (first four problems) and 49 in the

second half (last four problems). The data collected

were organized in a table containing, for each student

and for each of the 8 problems, the evaluations

relating to the five indicators of the assessment rubric

and the total score. The table was important both for

the analysis of the case study and for the analysis of

student assessments (the trend of total assessments

and the trend of assessments of individual indicators).

A significant and exemplary case study was

selected which showed an overall improvement in the

scores of the five indicators and whose competences

showed significant changes during the training. For

Assessment of Digital and Mathematical Problem-Solving Competences Development

321

the analysis of the case study, all the solutions to the

problems made by the student were analysed, and

some explanatory examples were reported. The

assessment rubric was used to analyze the

submissions, paying particular attention to the level

descriptors of each indicator. A correspondence was

sought between the assessments given by the tutors

and the competences achieved by the student, to

analyze in detail how they changed over time.

Furthermore, the educational value of personalized

feedback from tutors was examined. All of these

investigations made it possible to make a global

assessment of the progress of problem-solving and

digital competences in the selected case study.

A second level of analysis concerned all the

evaluations of the students in the sample, in order to

obtain a global vision and a more complete study of

the evolution of the students' competences. In order

to be able to effectively evaluate any improvement

between an initial and a final phase of the training, it

was necessary to examine the students who had

actively participated. For this reason, the analysis

sample was restricted to students who had solved at

least five problems (66 students in total), regardless

of what they were. After that, it was necessary to

identify a submission that represented the initial level

of competences and a final submission that

represented the level of competences achieved by

participating in the training. As the initial submission,

the one relating to the second problem was chosen,

because the first problem had fewer requests as it did

not ask for the generalization of the solution. This

further narrowed the sample to students who had

solved the second problem (61 students in total). The

last assignment completed by each student was

chosen as the final submission. For this part of the

analysis, we will call the second problem the “initial

problem” and the last submission problem the “final

problem”. We will call the total scores relating to the

initial problem "initial assessments" and those

relating to the final problem "final assessments". The

Wilcoxon signed rank test for paired samples was

then carried out with RStudio, to compare the initial

and final evaluations and measure any increases or

decreases. The Wilcoxon test was chosen because the

data did not represent a normal distribution. The test

made it possible to verify whether the difference

between the median of the initial evaluations and that

of the final evaluations was zero. Finally, to confirm

the results obtained from the test, the box-plots

relating to the initial evaluations and final evaluations

were created, which made it possible to deepen the

study.

To continue and further the analysis, we moved

on to study the development of the competences of

the 158 students of the initial sample during the entire

training. To carry out this analysis, the trend of the

arithmetic averages of the evaluations in the

individual indicators and in the total was studied.

Since the sample of the population on which the

averages were carried out varied over time and since

the outliers had a great influence on the arithmetic

mean, the box-plots relating to the evaluations were

created and analyzed, comparing the results of the

two analyses.

The students' answers to the final questionnaire

were analyzed to also consider the students' point of

view and to draw the final conclusions. 69 students

replied to the questionnaire. The questionnaire

contained questions relating to various aspects of the

project, such as: the degree of appreciation of the use

of ACE for problem solving; the usefulness of having

learned to use it; the difficulties encountered in

solving problems; the usefulness of developing

digital and problem-solving competences in the world

of work; a self-assessment of mathematical, problem-

solving and digital competences at the end of the

training. The typology of the questions is mainly

Likert scale questions, where students can select an

answer from 1 = “not at all” to 5 = “very much”. All

analyses were performed using Excel software and

RStudio statistical software.

4 RESULTS

4.1 Analysis of the Case Study

Through the analysis of the case study, it was possible

to observe a general improvement in problem-solving

and digital competences in the case of a student who

obtained a low score (below 50) in the first problem

and a high score in the last. The scores of the case

study (see Figure 1) start with a low initial evaluation

of 33/100, in the first half of the training it remains

approximately constant while, subsequently, there is

a significant improvement which sees an evaluation

of 93/100 in its last submission. The increase in the

degree of difficulty of the problems made it possible

to consider these results as particularly significant and

to select the student as a case study.

From the graph of the evaluation trends relating to

the individual indicators (see Figure 2) it is possible

to observe that all the indicators show a significant

improvement. They reflect the trend of the total

CSEDU 2023 - 15th International Conference on Computer Supported Education

322

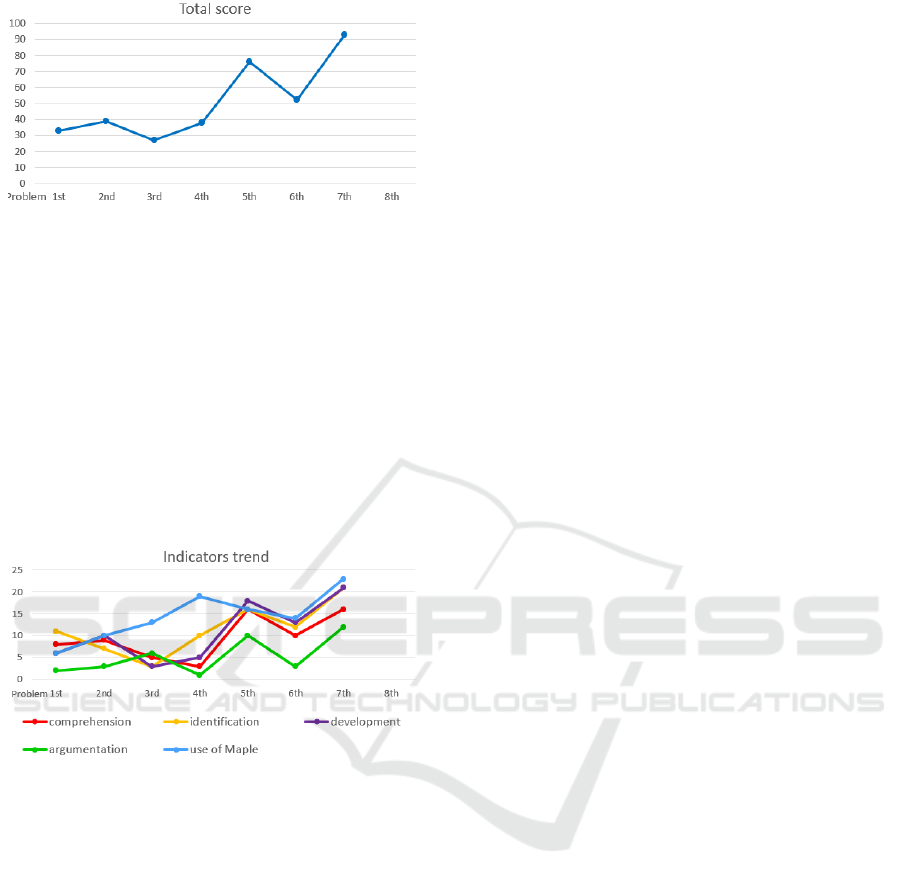
Figure 1: Trend of the overall assessments of the case study.

scores: starting from low evaluations, they show a

notable improvement in the second half of the

training, with the exception of the "use of Maple"

indicator which shows a progressive even if not linear

improvement during the entire training. As well as the

overall evaluations, also the evaluations of the single

indicators do not show a continuous and linear

improvement. Many factors influence this aspect: the

non-compulsory nature of the extracurricular project,

the progressive increase in the complexity of the

problems, school and personal commitments, the

mathematical knowledge possessed by the student.

Figure 2: Trend of the evaluations of the case study divided

by indicators.

The graph in Figure 2 shows an initial lowering of the

scores in the indicators "understanding the

problematic situation", "identifying a solution

strategy" and "developing the resolution process".

This may be due to the fact that the student is initially

not completely accustomed solving contextualized

problems and finds it difficult to solve problems with

increasing difficulty. At the same time, the

improvement of the indicators in the last submissions,

when the problems have a higher degree of

complexity, is particularly relevant. In the submission

of the first problem, the case study does not fully

develop the solution process. The student carries out

some calculations without arguing the steps taken and

the strategies chosen and provides a short final

answer to one of the questions in the problem. The

student uses the worksheet as a simple writing sheet

and is not familiar with Maple commands yet. In the

submission of the second problem the student still

does not develop and does not fully discuss the

proposed resolution. In this case, however, the

student tries to use the ACE to create an array of point

coordinates and to open packages with more

advanced commands (see Figure 3). Feedback from

tutors has been effective for student improvement.

The feedback for the resolution of the first problem

was: “The solution is only partially correct. The use

of Maple and the argument are poor but don't give up,

for the next problems it will be better! I advise you to

comment more on both the results found and the

individual steps". In the resolution of the second

problem, the student begins to comment on the

chosen strategies, such as: "I include "plots" to be

able to use the "pointplot" command"; "Imagining

that we have an exponential curve, the value that we

will have on the tenth day will be around 1600 new

cases"; "If you draw a line between the three points,

the new cases on the 19th day will be around 2500."

From the student's resolution and these last

comments, it is possible to notice how the student is

still unable to identify a solution strategy to model the

problem and to develop the resolution. The student

shows that they confuses exponential trend and linear

trend and demonstrates that he does not know how to

make the best use of the ACE. In fact, the student does

not obtain a mathematical expression that models the

problematic situation, and is not able to use the

commands to show a graph that adequately describes

it and for this reason he/she tries to "imagine" it.

In the submission of the third problem there is an

improvement in the use of Maple and in identifying

and implementing solution strategies for modeling

the problem. The student is still unable to identify the

correct strategies for modeling the problematic

situation, however he demonstrates originality and

creativity in developing the entire resolution through

an interactive component (see Figure 4). The

interactive component consists of an interactive table,

a slider and a text area. As the values of the slider

vary, the values of the last column of the table and the

result of the problem in the text area change. The

programming code to create the interactive

component (top right in Figure 4), shows the correct

use of the commands to take input data (for example:

parameter:=Do(%Slider0)) and return output values

(for example: Do(%TextArea0=parameter)). The

code also includes a nested loop. This represents an

improvement in programming proficiency. Despite

the originality of the problem-solving idea, it is not an

effective strategy due to a poor understanding of the

problem situation and the lack of identification of a

correct modeling.

Assessment of Digital and Mathematical Problem-Solving Competences Development

323

Figure 3: Solution of the second problem submitted by the

case study.

Figure 4: Resolution of the third problem submitted by the

case study.

During the training, the student's digital competences

gradually improve and it is possible to observe an

improvement also in the indicators "understanding

the problematic situation", "identifying a solution

strategy" and "developing the resolution process"

starting from the fifth problem. In the last submission,

despite a small error of understanding, the student

fully develops the resolution and implements

effective strategies, through modeling consistent with

the interpretation of the problem. The proposed

problem is contextualized in the advertising field, and

speaks of a disco that advertises its sound system.

Given the formula that describes the sound intensity

expressed in decibels (dB) as a function of the sound

intensity expressed in W/m2, the question was:

 to calculate the total sound intensity in dB of

four 100 dB loudspeakers, the one in dB of

each single loudspeaker knowing the total

loudness of 400 dB and to state whether the

declaration of the disco regarding its sound

system is capable of diffusing music at 400 dB

having four speakers of 100 dB each, correct or

tendentious;

 to construct an example that would show how,

given several speakers to which a different

sound intensity is associated, the total sound

intensity in dB could be approximated with that

of the speaker to which the greater intensity is

associated;

 to create a system of interactive components

which, given two loudspeakers to which two

sound intensities in dB are associated, would

return the total sound intensity in dB and at

least two graphs;

The student incorrectly understands the intensity

formula provided by the text, replacing the sound

intensity expressed in W/m2 with that expressed in

dB. Despite this, the development of the resolution of

the problem is interesting. For example, to find the

intensity of each single loudspeaker, the student

constructs a while loop which increases the total

intensity at each cycle, checking that the decibels

obtained with it do not exceed the maximum

threshold indicated by the problem. When the latter is

exceeded, the cycle returns the total intensity that

caused the maximum value to be exceeded. The total

intensity is then divided by 4 to obtain the intensity of

each individual speaker. This strategy allows to solve

the problem in a clear, schematic and effective way

by exploiting a piece of code that automatically

controls the steps to be carried out in order to obtain

the desired result under the conditions required by the

problem. For this reason, the student obtained the

highest marks for the indicators "identifying a

solution strategy" and "developing the solution

process" but not in "understanding the problematic

situation". The indicators in fact, as components of

problem solving, are closely related but, at the same

time, each of them has its own "identity" which

characterizes and distinguishes it from the others.

CSEDU 2023 - 15th International Conference on Computer Supported Education

324

During the training, the student’s argumentative

ability also improves: in the last submission the

student discusses the steps taken and the strategies

chosen, leading the reader to follow the reasoning

made. The results show that solving contextualized

problems with the ACE enhanced the student's

problem-solving and digital competences.

4.2 Analysis of the Assessments of all

Students

For the analysis of the evaluations of all the students,

the Wilcoxon test was carried out to evaluate any

improvement between an initial phase and a final

phase of the training. The p-value of 0.89>0.05 did

not allow us to reject the null hypothesis according to

which the medians of the initial evaluations and of the

final evaluations were equal. This result is

satisfactory for the purpose of this research. In fact,

since the final evaluations relate to problems of

greater difficulty, the equality or a non-significant

difference in the evaluations shows that the students

have developed competences to solve problems of

greater difficulty, suggesting an improvement in these

competences. This result was confirmed by the box-

plots relating to the initial and final evaluations (see

Figure 5).

Indeed, they show that the medians are the same,

with a value of 84/100, indicating a high starting level

(above 70) which becomes more significant when

related to the final submission, reflecting more

developed problem-solving and digital competences.

In the initial problem, the median is very close to the

third quartile indicating a high number of evaluations

between 84 and 89, while in the final problem 50% of

the evaluations are distributed symmetrically with

respect to the median with evaluations between 74

and 95. These results satisfy expectations: 25% of the

evaluations with a value greater than 84, which

initially was between 84 and 89, in the final problem

are distributed between 84 and 95, indicating that a

greater number of students took evaluations greater

than 89. At the same time, the first quartile passes

from corresponding to an evaluation of 72 to an

evaluation of 74, indicating that a greater number of

students have obtained an evaluation higher than 74.

The greater dispersion found in the final problem

compared to the initial problem can be justified by the

increase in the difficulty of the problems, which

therefore led to a greater variability of the

evaluations. At the same time, however, the

dispersion to the right of the median and the increase

in the value of the first quartile show a general

improvement in students' competences.

Figure 5: Box-plot of the overall evaluations related to the

initial and final problem.

By studying the trend of the average evaluations

during the entire training, it was possible to expand

the analysis and obtain a more complete vision of the

development of the students' problem-solving and

digital competences. The investigation of average

ratings showed an overall improvement in problem-

solving and digital competences. In fact, from the

graphs of the trend of the average evaluations of the

individual indicators and of the total ones (see Figure

6), a slight improvement can be observed for all the

indicators, even though not continuous or linear, with

a general decrease in the sixth problem. In particular,

the "argumentation" indicator shows a more evident

improvement, with a more regular trend and a

progressive improvement. This aspect indicates that,

although it was complex to understand, identify and

develop a solution strategy, the students were able to

explain and justify their resolution in an even more

precise, complete and pertinent way. In problem six

there is a drop in scores on all indicators. The

students' difficulties can also be seen in the

discussions in the forum on the platform: "Hi, I didn't

quite understand the third request"; "I wanted to ask

what was the exp function in the formula that I didn't

understand"; “Hi, regarding point 2 of the problem,

how did you do it (in a very general way)? Did you

use a more algebraic or graphical approach? Because

graphically it seems to me very complex to visualize,

while algebraically I find it more it difficult to find

the right commands". A slight worsening of all

Assessment of Digital and Mathematical Problem-Solving Competences Development

325

indicators in the second problem can also be

observed. This aspect is not surprising since the first

problem, being at the beginning of the training, had a

lower difficulty as it did not require the

generalization phase of the resolution, thus leading to

generally higher scores.

Since the arithmetic mean is influenced by

outliers, the latter may not effectively represent the

assessment of students' results during training. We

therefore decided to also analyze the median of the

total scores obtained during the training.

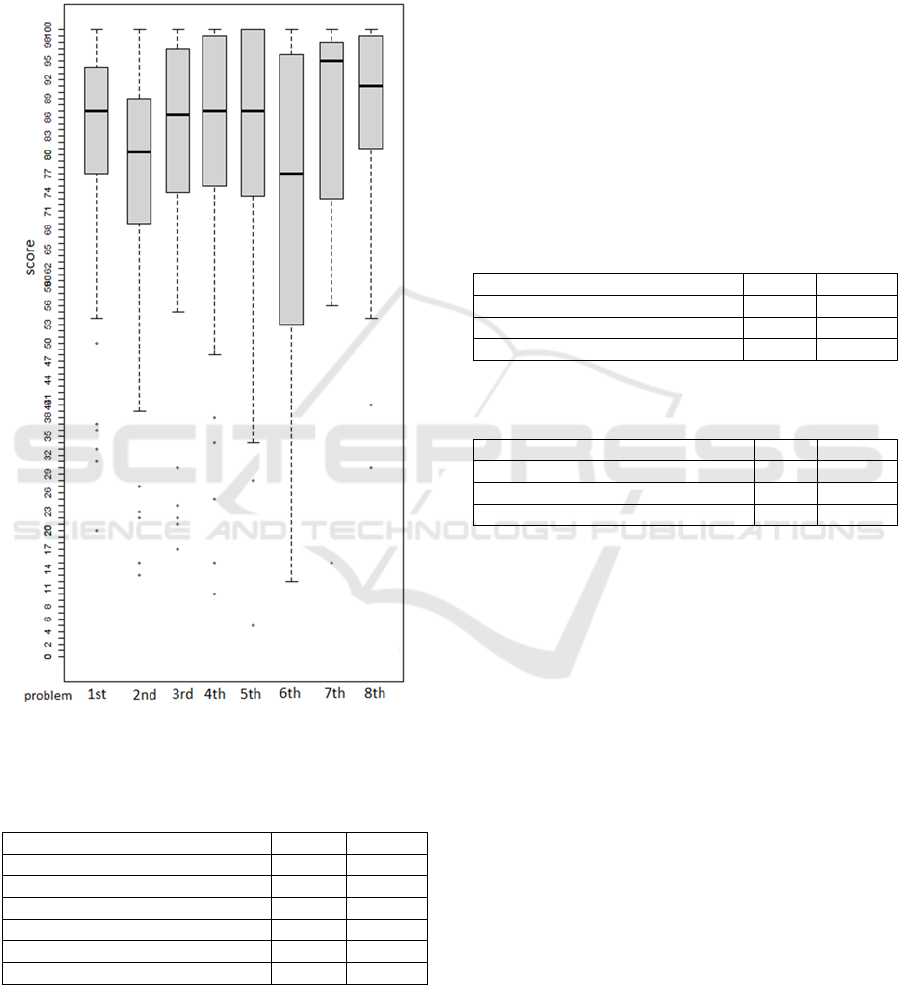
From the box-plots of the evaluations relating to

the total score (see Figure 7) it can be observed, for

each problem, a distribution of half of the evaluations

approximately symmetrical with respect to the

median and a generally reduced width of the

interquartile ranges, indicating a concentration of the

evaluations around the median. This indicates that the

median gives a good representation of the evaluation

obtained by the students.

In the sixth problem, the interquartile range is

instead wider, indicating a wider distribution of

evaluations. This implies that the median, in this case,

is less representative of the evaluations obtained by

all the students for that problem. This may be due to

the considerations made previously on the difficulty

encountered by the students in solving that problem.

In the seventh problem, however, the median

corresponds to an evaluation of 95/100 and is close to

the third quartile, indicating a large number of

submissions with a very high evaluation (above 95).

This justifies the peak that is also found in the graph

of average ratings. The trend of the medians is very

similar to that of the average evaluations of the

various indicators and of the total. For this reason, it

was possible to confirm what emerged from our the

analysis of the average ratings.

4.3 Analysis of Students' Answers to

the Final Questionnaire

The last part of the analysis concerned the students'

answers to the satisfaction questionnaire, to

understand their point of view on some aspects of

online training and on the development of their

competences. The first question examined was: "In

solving problems, which of the following aspects

gave you difficulty?". The answers (see Table 1)

show that the students found approximately the same

degree of difficulty in developing all the competences

related to the five indicators of the evaluation grid.

The average values of the answers are all between

3.13 and 3.20. Only the "argumentation" indicator

has an average response of 2.70, so students had less

Figure 6: Graphs of the trends of the average evaluations of

the single indicators.

CSEDU 2023 - 15th International Conference on Computer Supported Education

326

difficulty developing this skill. This is also confirmed

by the constant increase in ratings for this indicator.

These results reflect what was observed in the

analysis of the assessments of all students. In

particular, students experienced a slightly greater

difficulty in generalizing the problem, indicated by an

average of 3.48 out of 5.

Figure 7: Boxplot of the overall evaluations of all the

students.

Table 1: Students' answers to the question about the

difficulties encountered in solving problems.

Mean St.Dev.

Interpret the text 3.20 1.1

Identif

a solution strate

3.13 0.87

Com

lete the resolution

rocess 3.16 1.04

Discuss the solution 2.70 1.06

Generalize the problem 3.48 1.02

Use Maple 3.17 0.79

The second question examined was: "Please indicate

to what extent you think you have acquired the

following competences in online training". The

responses (see Table 2) indicate that, from the

students' point of view, participating in an online

training in a DLE and using an ACE for problem

solving fostered the development of their math,

digital and problem solving (with an average of 3.12,

3.46, 3.52 respectively). The third question examined

was: "Please indicate to what extent you think these

competences will be useful in the world of work".

Table 3 shows the results. It is interesting to observe

how students find mathematical competences (with

an average of 3.60) and problem-solving and digital

competences (with an average of 4.19 and 4.25

respectively) useful in the world of work, revealing

the strong awareness of importance of these

competences for their future, even outside the school

context.

Table 2: Students' answers to the question on the

development of their competences.

uired com

etences Mean St.Dev.

Mathematical com

etences 3.12 0.72

ital com

etences 3.46 0.70

Problem-solving competences 3.52 0.85

Table 3: Students' answers to the question on the usefulness

of the competences in the world of work.

Utility in the world of wor

Mean St.Dev.

Mathematical competences 3.60 0.89

Digital competences 4.25 0.72

Problem-solvin

com

etences 4.19 0.81

The last question analyzed concerned the school

average of the students in mathematics (expressed by

the students in a grade from 1 to 10) at the beginning

and at the end of the online training. For 30% of the

students the average improved, for 67% of the

students the average remained unchanged and for 3%

of the students the average worsened. In particular,

the average decreased only in two students who went

respectively from 10 to 9.5 and from 8 to 6.

Furthermore, 55% of the students whose average

remained unchanged had a high starting average

(above 8) . For this reason, the results obtained are

satisfactory and show a general improvement in the

mathematical competence of the students

participating in the online training.

5 CONCLUSIONS

This research work had the main objective of

evaluating the development of problem-solving and

digital competences of secondary school students

who carry out problem-solving activities with an

Assessment of Digital and Mathematical Problem-Solving Competences Development

327

ACE during an online training in a DLE. To answer

the research question, the online training of grade 12

students from the 2021/2022 school year edition of

the DMT project was examined. The analysis was

developed following three phases: the analysis of an

exemplary case study; the analysis of all student

evaluations; the analysis of the students' answers to

the final questionnaire submitted at the end of the

training. The results show that the problem-solving

activities with an ACE carried out during the online

training allowed the development of all problem-

solving competences (in particular argumentation)

and digital competences. In fact, the use of an ACE in

problem solving has made it possible to support all

phases of problem solving, allowing to focus on the

resolution process, on exploration and on the results

obtained, and to exploit different types of

representation in the same environment. Furthermore,

the ACE, with the creation of interactive components,

has favored the process of generalization of the

problem, an important phase of problem solving

which, from what emerged from the questionnaire, is

considered difficult to tackle by students. In the

generalization phase students have to design and

program the interactive components in such a way

that they take data as input, process a result and return

an output of the results of the problem. In this way, it

is possible to generalize the initial situation and see

how the solution of the problem changes as the initial

data vary. This is not easy but it allows them to

develop abstraction and programming competences

using a specific language. The growing difficulty of

the problems has also helped to foster the

development of problem-solving and digital

competences, stimulating the commitment,

participation and training of the students, who in this

way have developed and consolidated their

competences.

The analysis of the case study submissions

showed that the evaluation system had a positive

impact on the development of students' competences.

The personalized feedback from the tutors and the

comparison of the evaluations obtained with the

shared assessment rubric have allowed the students to

establish their own level of competence and to

understand what and how to improve, which are the

three important processes of formative assessment

(Black & Wiliam, 2009).

Since the development of problem-solving and

digital competences, key competences for lifelong

learning and problem-solving activities with an ACE

are also part of the institutional objectives, it is

desirable to promote these activities within the school

context, entrusting the competences of problem-

solving and digital skills a central role in teaching.

A limitation of this study is the variation in the

number of students who turned in problem resolutions

over the course of training. Future research could

propose problem-solving activities with an ACE

during lessons at school, in order to carry out the

analysis on a sample of students that does not vary

over time. It would be interesting to compare the

development of problem-solving and digital

competences using a control sample of the same

education level, made up of students who do not

participate in the activities. In this way it would be

possible to further evaluate the effectiveness of

problem-solving activities with an ACE for the

development of these competences. However, this is

not easy because some problem requests would be

difficult to implement without the use of

technologies. This type of project shows how

technology can be used naturally in ordinary

teaching. It allows the teacher to rethink the teaching

methods, and at the same allows the student to

develop mathematical, digital and problem-solving

competences.

REFERENCES

Barana, A., Boetti, G., & Marchisio, M. (2022). Self-

Assessment in the Development of Mathematical

Problem-Solving Skills. Education Sciences, 12(2), 81.

https://doi.org/10.3390/educsci12020081

Barana, A., Brancaccio, A., Conte, A., Fissore, C., Floris,

F., Marchisio, M., & Pardini, C. (2019). The Role of an

Advanced Computing Environment in Teaching and

Learning Mathematics through Problem Posing and

Solving. Proceedings of the 15th International

Scientific Conference ELearning and Software for

Education, 2, 11–18. https://doi.org/10.12753/2066-

026X-19-070

Barana, A., Conte, A., Fissore, C., Floris, F., Marchisio, M.,

& Sacchet, M. (2020). The Creation of Animated

Graphs to Develop Computational Thinking and

Support STEM Education. In J. Gerhard & I. Kotsireas

(Eds.), Maple in Mathematics Education and Research

(pp. 189–204). Springer. https://doi.org/10.1007/978-3-

030-41258-6_14

Barana, A., & Marchisio, M. (2022). A Model for the

Analysis of the Interactions in a Digital Learning

Environment During Mathematical Activities. In B.

Csapó & J. Uhomoibhi (Eds.), Computer Supported

Education (Vol. 1624, pp. 429–448). Springer

International Publishing. https://doi.org/10.1007/978-

3-031-14756-2_21

Barana, A., & Marchisio, M. (2016). From digital mate

training experience to alternating school work

activities. Mondo Digitale, 15(64), 63–82.

CSEDU 2023 - 15th International Conference on Computer Supported Education

328

Barana, A., Marchisio, M., & Sacchet, M. (2021).

Interactive Feedback for Learning Mathematics in a

Digital Learning Environment. Education Sciences,

11(6), 279. https://doi.org/10.3390/educsci11060279

Black, P., & Wiliam, D. (2009). Developing the theory of

formative assessment. Educational Assessment,

Evaluation and Accountability, 21(1), 5–31.

https://doi.org/10.1007/s11092-008-9068-5

Brancaccio, A., Marchisio, M., Meneghini, C., & Pardini,

C. (2015). More SMART Mathematics and Science for

teaching and learning. Mondo Digitale, 14(58), 1-8.

Baroni, M., & Bonotto, C. (2015). Problem posing e

problem solving nella scuola dell’obbligo. 62.

Fondazione Giovanni Agnelli. (2010). Rapporto sulla

Scuola in Italia.

D’Amore, B., & Fandiño Pinilla, M. I. (2006). Che

problema i problemi. L’insegnamento della matematica

e delle scienze integrate, 6(29), 645-664.

European Parliament and Council. (2018). Council

Recommendation of 22 May 2018 on key competences

for lifelong learning. Official Journal of the European

Union, 1–13.

Hattie, J., & Timperley, H. (2007). The Power of Feedback.

Review of Educational Research, 77(1), 81–112.

https://doi.org/10.3102/003465430298487

Jonassen, D. H. (2014). Assessing Problem Solving. In J.

M. Spector, M. D. Merrill, J. Elen, & M. J. Bishop

(Eds.), Handbook of Research on Educational

Communications and Technology (pp. 269–288).

Springer New York. https://doi.org/10.1007/978-1-

4614-3185-5_22

Leong, Y. H., & Janjaruporn, R. (2015). Teaching of

Problem Solving in School Mathematics Classrooms.

In S. J. Cho (Ed.), The Proceedings of the 12th

International Congress on Mathematical Education

(pp. 645–648). Springer International Publishing.

https://doi.org/10.1007/978-3-319-12688-3_79

Liljedahl, P.; Santos-Trigo, M.; Malaspina, U.; Bruder, R.

(2016). Problem Solving in Mathematics Education,

New York, NY: Springer Berlin Heidelberg.

Malara, N. A. (2012). Processi di generalizzazione

nell’insegnamento-apprendimento dell’algebra. Annali

online della Didattica e della Formazione Docente,

4(4), 13-35.

MIUR (2010). Schema di regolamento recante “Indicazioni

nazionali riguardanti gli obiettivi specifici di

apprendimento concernenti le attività e gli

insegnamenti compresi nei piani degli studi previsti per

i percorsi liceali". Roma.

National Council of Teachers of Mathematics (2000).

Executive Summary Principles and standards for school

Mathematics.

Polya, G. (1945). How to solve it. Princeton university

press.

Samo, D. D., Darhim, D., & Kartasasmita, B. (2017).

Culture-Based Contextual Learning to Increase

Problem-Solving Ability of First Year University

Student. Journal on Mathematics Education, 9(1), 81–

94. https://doi.org/10.22342/jme.9.1.4125.81-94

Suhonen, J. (2005). A formative development method for

digital learning environments in sparse learning

communities [University of Joensuu]. http://

epublications.uef.fi/pub/urn_isbn_952-458-663-

0/index_en.html.

Assessment of Digital and Mathematical Problem-Solving Competences Development

329