Privacy-Preserving Algorithms for Data Cooperatives with Directed

Graphs

Mark Dockendorf and Ram Dantu

Department of Computer Science, University of North Texas, 1155 Union Cir, Denton, TX, U.S.A.

Keywords:

Data Cooperatives, Privacy, Applications of Homomorphic Encryption (HE), Graph Algorithms, Encrypted

Graphs.

Abstract:

A handful of companies currently hold large collections of data about most people. In addition to the question-

able ethics of collecting personal data with few-to-no options to limit what these companies collect, there exist

exceptionally few ways to regulate how your data is stored and used once it is collected. Furthermore, these

data collections cannot be easily cross-referenced to gain insight. Data cooperatives provide an alternative to

these separated collections of data. As a participant-driven organization, similar to a credit union, data cooper-

atives have a vested interest in preserving the privacy of individuals while offering insight similar to other big

data analytics. Another bonus of the data cooperative model is the voluntary (and ethical) sourcing of data. The

downside of giving participants the freedom to choose which data they contribute is incomplete data sets. To

help address this, we adapt label propagation, a semi-supervised learning algorithm for community detection

based on partially labeled data, to work over homomorphically encrypted (HE) graphs. We also adapt triangle

counting and a vertex scoring scheme to work over directed heterogeneous-vertex, heterogeneous-edge HE

graph data.

1 INTRODUCTION

1.1 Data Cooperatives

Data cooperatives provide an alternative to traditional

large data collections. A data cooperative is the vol-

untary collaborative pooling of data by individuals

for the beneﬁt of the group or community (Pentland

and Hardjono, 2020). Unlike current big data solu-

tions, data cooperatives are participant-driven, volun-

tary collections of data. This differs from the cur-

rent “data silos” held by a handful of organizations

(FAANG, governments, etc.) in that data and insights

derived from it can be had by anyone, not just those

that have these data collections. Furthermore, the spe-

ciﬁc insights delivered are custom to the questions

asked by the data consumer, not a set of generic in-

dicators.

As all data collection is voluntary, data coopera-

tives can serve as ethical data sources. If a participant

does not wish to share a particular type of data, they

are not forced to do so.

This leads to mixed levels of data sharing among

participants and contributes to the issue of incomplete

data within the cooperative. This is compounded with

the fact that of the many possible participants, a sig-

niﬁcant number will not be sharing data at all.

1.2 Homomorphic Encryption (HE)

Homomorphic encryption (HE) allows for computa-

tion over ciphertext values using speciﬁc functions.

There exists a homomorphism between these func-

tions and cleartext operators such as addition, mul-

tiplication, etc.

Some common HE schemes include BFV, which

allows for addition and multiplication of encrypted in-

tegers (Fan and Vercauteren, 2012); HEAAN/CKKS,

which allows for addition and multiplication of block

ﬂoating point values (Cheon et al., 2017); and TFHE,

which allows for the evaluation of binary gates over

ciphertext values (Chillotti et al., 2019) (Chillotti

et al., 2016). CHIMERA (Boura et al., 2020) de-

scribes a method of converting between all three of

the aforementioned schemes without decrypting.

We use HE in our data cooperative to protect per-

sonal data in case of a data breach, a snooping 3rd

party, or a cooperative that betrays the participants.

We will achieve this by using a multikey HE (Chen

et al., 2019)(L

opez-Alt et al., 2017) where the key is

876

Dockendorf, M. and Dantu, R.

Privacy-Preserving Algorithms for Data Cooperatives with Directed Graphs.

DOI: 10.5220/0012140200003555

In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 876-884

ISBN: 978-989-758-666-8; ISSN: 2184-7711

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

divided among the participants and the cooperative.

Thus, the cooperative will need the cooperation of the

participants in order to decrypt any query result that

uses private information as described in our previous

work (Dockendorf and Dantu, 2023).

1.3 Related Work

1.3.1 Data Privacy Survey

According to GDMA’s 2022 global data privacy sur-

vey (GDMA and Acxiom, 2022), 48% of US respon-

dents are data pragmatists: willing to share data if

there is a clear beneﬁt to it, and 31% of US respon-

dents are data unconcerned: not caring how their data

is used. Their survey further ﬁnds that “data funda-

mentalists”, those who are unwilling to share data, ac-

count for approximately 21% of US respondents, with

79% of US respondents “willing to engage in the data

economy”.

We would like to note that as an online survey,

GDMA’s research possibly missed the most privacy-

concerned among the populace as such individuals

may not be willing to answer an online survey. Typ-

ically, online surveys have a response rate below

30% (Nayak and Narayan, 2019)(Lindemann, 2023).

While this percentage is not reported in the survey,

the survey shows that among respondents, people are

becoming more willing to share their data.

1.3.2 HE for Data Cooperatives

We have adapted (and benchmarked) several graph

algorithms to work over HE graph data with spe-

cial consideration given to a data cooperative use-

case (Dockendorf et al., 2021) (Dockendorf. et al.,

2022). The algorithms adapted to work over HE

graph data include ring-based BFS, vertex degree,

farness centrality, Bellman-Ford (single-source short-

est path), Floyd-Warshall (all-pairs shortest path),

Kruskal (minimum spanning forest), betweenness

centrality, and random walk.

We use HE in our data cooperative to provide pri-

vacy by encrypting edges that constitute PII. As an

example, an edge representing residence between a

vertex representing a person and and a vertex repre-

senting a plot of land would be encrypted as a home

address is considered PII.

1.3.3 HE Undirected Triangle Counting

The authors of CryptGraph (Xie and Xing, 2014)

showed results for computing the clustering coefﬁ-

cient of an undirected HE graph, which, as a subrou-

tine, requires triangle counting. This year, a paper

detailing structural encryption for graphs with accu-

rate triangle counting is set to publish (Wu and Chen,

2023).

Our results differ from the aforementioned works

as we count directed triangles, where these works

only considered undirected triangles. Distributed tri-

angle counting has also been previously explored with

performance sufﬁcient for “small and medium size

data” (Do and Ng, 2016). This work is also the most

similar to ours conceptually, despite being distributed,

as each party contributes edges from their perspec-

tive as participants in our data cooperative would con-

tribute their outgoing edges from their perspective.

2 MOTIVATION

2.1 Incomplete Data

Naturally, as some potential data cooperative partici-

pants will not join due to privacy concerns, any data

cooperative will have to work with incomplete data.

This is further compounded by the fact that partici-

pants are not required to share all data types. As such,

certain data that some participants are unwilling to

share will be incomplete, even among active partic-

ipants.

This is further compounded by the fact that not

all participants will provide updates at the same rate.

This difference in update rate may lead to temporary

inconsistencies in the data.

2.2 Graph Database

Our model for a data cooperative uses a graph

database. Graph databases provide more ﬂexibility

than rigid-schema databases, allowing the cooperative

to accommodate varying levels of data contribution

from participants and adapt more quickly to chang-

ing data needs of data consumers. Furthermore, many

graph algorithms are useful for extracting metrics and

data insight from the collected data (Robinson et al.,

2015).

Graph algorithms can be used to predict social me-

dia activity (Pitas, 2016), detect money laundering

(Li et al., 2020), optimize supply chains (Robinson

et al., 2015), and much more. To put it plainly, storing

data in graph form facilitates the production of data

insight, the primary product of a data cooperative.

A number of existing graph algorithms have already

been adapted to work over HE graph data (Dock-

endorf. et al., 2022) (Dockendorf et al., 2021)(Xie

and Xing, 2014).

Privacy-Preserving Algorithms for Data Cooperatives with Directed Graphs

877

Finally, since participants submit data from their

point of view, they are effectively submitting directed

graph data (outgoing edges from their perspective).

This is why all of our HE graph algorithms speciﬁ-

cally accommodate directed graph data.

3 OUR CONTRIBUTION

In this paper, we demonstrate three algorithms over

HE graph data: HE label propagation, HE directed

triangle counting, and HE weighted triangle creation

vertex scoring. We touch on issues that data cooper-

atives using HE will face related to incomplete data

and propose HE label propagation for inferring data

without disclosing labels to the cooperative. Label

propagation is an algorithm for inferring communi-

ties given a set of known values (labeled vertices) and

a graph which has edges that are a good indicator of

communities.

We demonstrate a variant of label propagation de-

signed to work over HE graph data given an encrypted

labeled vertex set. This algorithm achieves the same

result as its cleartext counterpart with O(r ∗ S(|V |))

runtime complexity, where S(|V |) is the time com-

plexity of squaring a |V | by |V | matrix, |V | is the

number of vertices in the graph, and r is the re-

peated square count to produce the desired conver-

gence. This algorithm can be used by data cooper-

atives to infer labels of previously unlabeled vertices

given a graph that is a good indicator of the labels

in question, all without disclosing any previously-

unknown information. Thus, HE label propagation

can offer a solution to data cooperatives for certain

types of incomplete data.

We demonstrate directed triangle counting over

HE graph data. We deﬁne three types of directed tri-

angles: true, strong, and weak and benchmark our HE

graph algorithms for counting these.

Finally, we provide an example of weighted trian-

gle creation vertex scoring over HE graph data. This

scoring method places different weights based on the

types of triangles that would be created should an

edge be added between a given vertex and any one of

the candidate vertices. These weights are tuned based

on which shared neighbor vertices and edge types are

more desirable. This algorithm has a variety of appli-

cations, including multi-factor friend suggestion and

network security risk assessments.

4 ALGORITHMS

4.1 HE Label Propagation

4.1.1 Cleartext Algorithm

Cleartext label propagation is as follows (Raghavan

et al., 2007):

1. Initialize the labels at all vertices in the network.

For a given vertex x, C

(0) = x.

2. t := 1

3. Randomize the order of vertices and set it to X.

4. For each x ∈ X chosen in that speciﬁc or-

der, let C

(t) = f (C

(t),...,C

(t),C

i(m+1)

(t −

1),...,C

(t − 1)). Return the label occurring with

the highest frequency among neighbours (select

random label on tie).

5. If every vertex has a label that the maximum num-

ber of their neighbours have, then stop the algo-

rithm. Else, t := t + 1 and goto (3).

Naturally, the conditional jump in 5 above must

be eliminated in order to create a HE algorithm as the

program counter cannot be updated based on an en-

crypted value. Thus t will iterate until the maximum

possible steps for full propagation on a given graph or

will terminate after a user-deﬁned number of steps (if

the user speciﬁes a number of iterations less than the

maximum number of steps).

4.1.2 HE Algorithm

Homomorphic label propagation with weighted prob-

ability for transition works on the same premise as

cleartext label propagation. To initialize, we create a

|V | by |V | matrix, A. For each vertex of the graph,

if the vertex is labeled, place a 1 on the diagonal of

A and zero in all other columns; otherwise, invert all

values, with 0 inverting to 0, and store to A. Next,

sum each row of A and divide all values in the row

by the sum; this normalizes the sum of each row of A

to 1. Finally, repeatedly square A until convergence

(r times). This convergence threshold, which is the

repeated square count, r, is passed as an argument to

homomorphic label propagation.

To get around the conditional termination of clear-

text label propagation, homomorphic label propaga-

tion uses a repeated square count. This value can be

tuned based on the number of values in the graph. For

all experiments in this paper, the value was 5; this

means that the A matrix is repeatedly squared 5 times,

resulting in A

= A

. A good repeated square count

for real-world data may be 7, which would result in

128

SECRYPT 2023 - 20th International Conference on Security and Cryptography

878

While the number of vertices, |V |, is the primary

contributor to the algorithm’s growth rate, the re-

peated square count, r, contributes multiplicatively to

the algorithm’s growth rate. Luckily, a small r value

can still be very effective in converging the labels: this

is due to the fact that convergence is exponential in

nature (due to repeated squaring). Since A is a |V |

by |V | matrix and naive matrix multiply is O(|V |

the overall complexity for label propagation ends up

O(r|V |

). A faster HE matrix multiplication or squar-

ing algorithm will beneﬁt HE label propagation.

Parallel HE Label Propagation

Input: G, the encrypted graph; L, encrypted set of la-

beled vertices; r, repeated square count

Output: A, encrypted label matrix

A, B, are zero-initialized |V| by |V| matrices

#parallel loop

for every edge in G[i,j]:

if i = j:

A[i,j] := (L[i]) ? 1 : A[i,j]

else:

A[i,j] := (!L[i]) ? G[i,j] : A[i,j]

#parallel loop

for each row, i, in A:

row_sum := 0

for each column, j, in A:

A[i,j] := (A[i,j] != 0) ? 1/A[i,j] : 0

row_sum := row_sum + A[i,j]

norm := (row_sum != 0) ? 1/row_sum : 0

for each column, j, in A:

A[i,j] := A[i,j] * norm

for k := 1 to r:

B := parallel_mm(A,A)

pointer swap B <-> A

return A

In the pseudocode above, parallel mm is a par-

allel matrix multiplication algorithm with at least

O(|V |) parallelism. This results in O(r|V |

) growth

complexity with up to O(|V |) parallelism or SIMD as

is possible with packed ciphertexts (a single cipher-

text containing multiple values, resulting in SIMD op-

erations).

We also make use of the HE MUX, similar to our

work in (Dockendorf. et al., 2022), which is repre-

sented in our pseudocode by the ternary operator. The

HE MUX is represented above as a ternary operator.

Given the expression (!L[i])?G[i,j]:A[i,j], ﬁrst

c = !(L[i] != 0) is evaluated. Then the result, c,

a TFHE bit, is fed into the control of a TFHE MUX

circuit, which selects G[i,j] if c is an encrypted 1

and selects A[i,j] otherwise. This enables condi-

tional evaluation under HE so that one could use a

restricted if/else structure in an HE context, but re-

quires evaluation of both the if and else path before

committing results.

4.1.3 Equivalence to Cleartext Label

Propagation

Label propagaion is based on a simple premise: ran-

dom walk. Let us consider all labeled vertices, in set

L, to be absorbing: that is, once they are reached,

the random walk cannot transition to another vertex.

Thus, once a labeled vertex is reached, the walk will

end on that vertex, and a random walk started from a

labeled vertex will end on that same vertex. This is

expected and desired as vertices in L have known la-

bels. We encode this as a 1 on the diagonal of the A

matrix and all other values on that row as 0.

If a walk is started from an unlabeled vertex, a

vertex not in L, we need to determine the probability

that the walk of inﬁnite length will end at any given

vertex. A walk of inﬁnite length could only “end” at

an absorbing state: a vertex in L. To determine this,

we ﬁrst ﬁgure out the probability of transitioning to

all neighbors, then to neighbors of neighbors, and so

on until eventually reaching an absorbing state.

We assemble matrix, A, that contains the probabil-

ity of transition by inverting outgoing edge weights

(assuming higher weights are more prohibitive to

transitioning across the edge, otherwise inversion is

skipped) and then summing the inverted values. The

total weight for each row is then inverted and the en-

tire row is multiplied by this value: this normalizes

the sum of each row to 1 with each entry being the

probability that a transition from vertex i to vertex j

occurring located at A

i j

This A matrix is then repeatedly squared to pro-

duce convergence, where each unlabeled vertex’s

probability of ending up at a labeled vertex is present

in the labeled vertices’ columns.

4.1.4 Data Cooperative Optimization

In producing the A matrix, we assumed encrypted la-

bels to give the algorithm the ability to run over all-

encrypted data. However, if data is either provided

(labeled) or not provided (unlabeled) by a participant,

the cooperative could know whether a vertex was la-

beled or not. This knowledge allows for several small

optimizations.

The ﬁrst parallel loop in the pseudocode could be

optimized to a copy based on a cleartext conditional

rather than a set of HE MUXes: this saves O(|V |

)

TFHE bootstrappings.

In the second parallel loop, we know that every

labeled vertex will have a row that is all 0 other than a

single 1 on the diagonal. This allows us to skip those

rows as they are already normalized to 1: this reduces

required bootstrappings by a factor of |L|/|V |.

Finally, within the matrix squaring algorithm, we

Privacy-Preserving Algorithms for Data Cooperatives with Directed Graphs

879

know that labeled rows will not change: they will

remain a 1 on the diagonal with all other values 0.

This allows for optimization by skipping calculation

of those rows (as they will not change) and storing

those rows as cleartext, which reduces the number of

bootstrappings required in the matrix squaring algo-

rithm (the number of bootstrappings saved is depen-

dent on the squaring algorithm used and proportion of

labeled vertices).

4.2 Directed Triangles

Triangle counting is an important graph metric and

is used as part of calculating certain other metrics,

including clustering coefﬁcients (Holland and Lein-

hardt, 1971)(Watts and Strogatz, 1998). Due to the

nature of a data cooperative accepting data from par-

ticipants, the data submitted to the cooperative will be

from the perspective of each participant. This means

that data submitted to the cooperative is directed, with

each participant supplying their outgoing edges. We

adapt the triangle deﬁnition to directed graphs and im-

plement HE directed triangle counting.

4.2.1 True Triangle

As triangles in an undirected graph are complete sub-

graphs on 3 vertices, a true triangle in a directed

graph is also a complete subgraph on 3 vertices. Con-

sequently, a true triangle can be detected by identify-

ing a reversible 3-cycle. That is to say, any set of 3

vertices forming a triangle with a return link for each

edge in the triangle constitutes a true triangle. Thus,

if a true triangle has vertices v

, v

, and v

, then:

true

i jk

⇒ v

→ v

∧v

→ v

(1)

4.2.2 Strong Triangle

A strong triangle loosens the deﬁnition of a true trian-

gle to a strongly-connected 3-vertex subgraph. A 3-

cycle subgraph in a directed graph that does not share

the same vertex set as any triangle that has already

been counted would then be a unique triangle. That

is to say, each 3-cycle is counted once, but only if its

reverse has not already been counted: this prevents

strong triangle counting from reporting true triangles

as 2 triangles.

strong

i jk

⇒ v

→ v

∨ v

→ v

(2)

4.2.3 Weak Triangle

A weak triangle further loosens the deﬁnition of a

triangle to any weakly-connected 3-vertex subgraph.

For a triangle to be weak, one of its vertices must have

only incoming or only outgoing edges. When data is

expected to have return edges for all edges, the per-

vertex ratio of weak triangles to true triangles can be

used as an indicator for which vertices may have out-

dated or inconsistent data.

4.2.4 Triangle Types

With each deﬁnition including more 3-vertex struc-

tures, the following relationship can be observed for

the different sets of directed triangles:

true

⊆ T

strong

⊆ T

weak

(3)

4.3 HE Weighted Triangle-Creation

Scoring

There are many applications of vertex scoring, includ-

ing friend suggestions (in social networks), risk as-

sessment, and network security. Weighted triangle-

creation scoring is particularly suited for heteroge-

neous graphs, those that have multiple types of ver-

tices and edges, as each type of potential triangle can

have its own associated weight. We call this triangle-

creation scoring as vertices are scored based on the

number and type of triangles that will be created in

the graph should the proposed edge be added.

We demonstrate, as an example, a simple

weighted triangle-creation scoring that can be used

to generate friend suggestions for hobbies and other

in-person activities. The query steps are as follows:

1. Start from a list of all people.

2. Filter out subject’s current friends.

3. Filter out people that do not share at least one

common location with subject.

4. Add points for each activity interest shared with

subject (triangle type a).

5. Add points for each friend shared with subject

(triangle type f ).

6. Return score vector.

If the result is to be disclosed to a 3rd party,

only a short list can be sent. This can be

achieved by making a 2-tuple out of each vector slot:

(person uuid,score). These tuples would then be

sorted by their score and the top-k results returned.

Examples include “top-5 friend recommendations for

SECRYPT 2023 - 20th International Conference on Security and Cryptography

880

Figure 1: An example (in cleartext) of weighted triangle-creation scoring: multi-factor friend suggestion in a social network.

The candidates (in yellow) were selected by ﬁltering all people down to those that shared at least one common location with

our subject (blue circle). Candidates are then scored based on the number and type of edge shared with friends (green) of our

subject and activity interests (in red) of our subject. Three scores and rankings are given in this example, with a being the

value of a shared activity interest and f being the value of a shared friend. Of particular interest are the candidates with a red

arrow as their rankings vary signiﬁcantly when a and f are adjusted. The sum of the coefﬁcients of the considered factors (a’s

and f ’s coefﬁcients in this example) is the number of triangles that will be created if that candidate is selected and an edge is

added. Analysis similar to this could also be applied to network security and risk management.

Figure 2: The two types of triangles considered in our ex-

ample of HE weighted triangle creation scoring. The “pro-

posed edge” is dotted at the bottom of both triangles. Cir-

cles represent people, while squares represent activities;

further, black edges indicate friendship, while orange edges

indicate participation. Type ‘a’ is a heterogeneous-vertex,

heterogeneous-edge weak triangle where both people par-

ticipate in a shared activity. Type ‘f’ is a homogeneous-

vertex, homogeneous-edge true triangle where both the can-

didate (yellow) and the subject (blue) have a shared friend

(green).

hobbies you enjoy”, “top-8 servers by potential ﬁnan-

cial damage if breached by an attacker”, etc.

Importantly, scores for creating different types of

triangles do not have to be and generally should not

be the same. For example, if the subject is looking

for someone to join a tight-knit group of friends for

an activity, shared friendships may be more impor-

tant than shared activity interest. As another example,

the ﬁnancial risk of a breach on a server that handles

payment information is generally higher than one that

only serves images or static web pages.

5 EXPERIMENTAL RESULTS

All experiments were performed using TFHE encryp-

tion with 128-bit equivalent security (Chillotti et al.,

2016) on an AMD 3960X using individual (non-

packed) ciphertexts. We use a single-key scheme to

demonstrate the validity of these algorithms in a gen-

eral TFHE or CHIMERA context. A ﬁnal product

would use a multi-key CHIMERA (or similar) con-

text with threshold decryption to split the key among

participants.

5.1 HE Label Propagation

Label propagation results are slow at this stage,

mostly due to using TFHE. We use TFHE for the in-

version step as inversion is currently unsupported by

the other standardized HE (Albrecht et al., 2018).

HE label propagation’s runtime is dominated by

the naive parallel matrix multiply, which has O(|V |

)

runtime. Using a more efﬁcient matrix multiplica-

tion or matrix squaring algorithm would greatly bene-

Privacy-Preserving Algorithms for Data Cooperatives with Directed Graphs

881

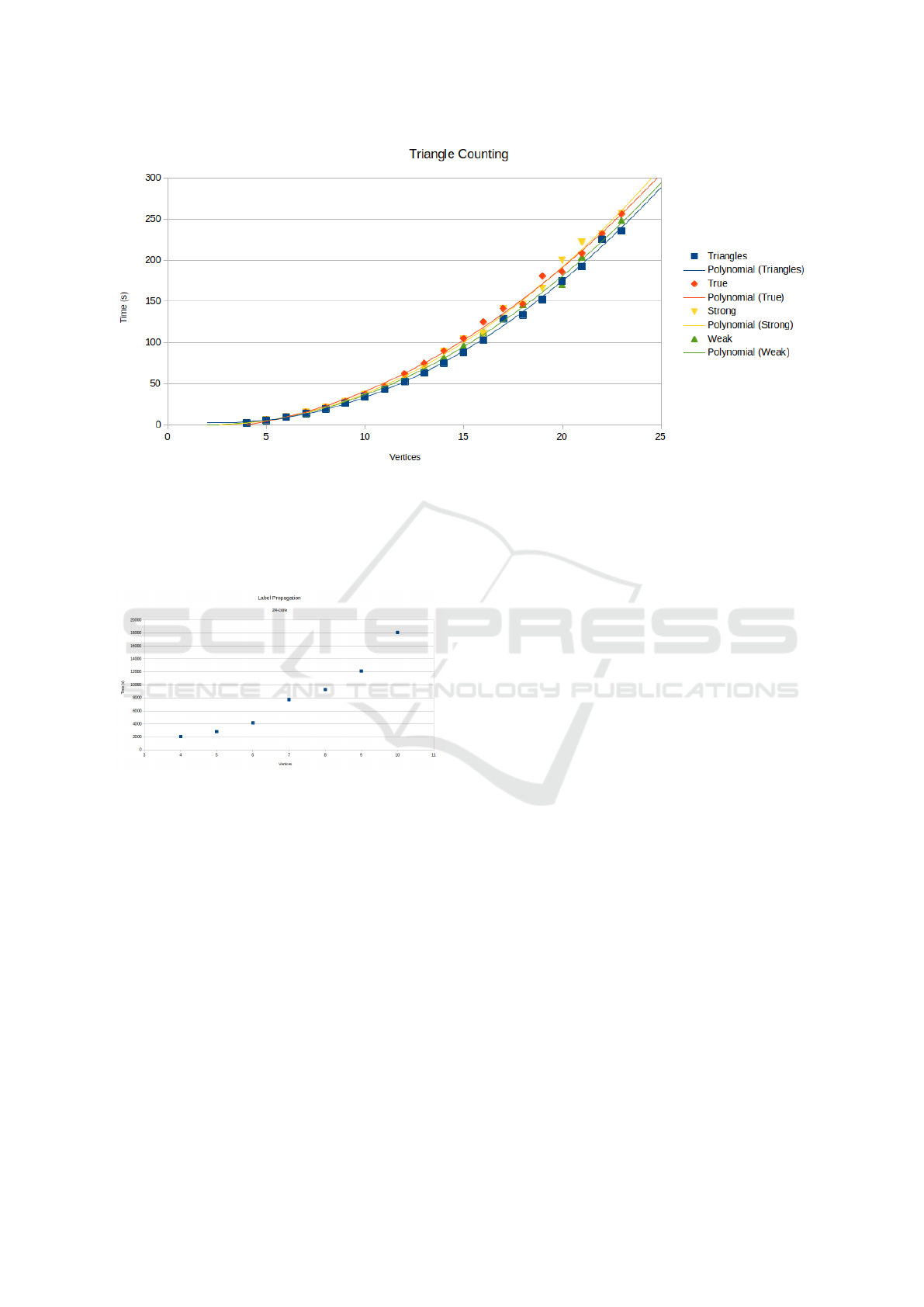
Figure 3: Timing results for all forms of triangle counting over HE graphs. Only “triangles” is performed on an undirected

graph; all others are for directed graphs. All-in-all, other than a scaling factor, the time taken grows with O(|V |

) when O(|V |)

parallelism is available. Linear time (single-thread) growth rate is O(|V |

) as a result of graph sparsity being held constant at

75% (25% of possible edges are present in the graph). Triangle counting in undirected graphs is fastest, with weak triangle

counting on directed graphs being second-fastest. Strong and true triangle counting are roughly tied in terms of performance;

however all grow the same asymptotically.

Figure 4: Label propagation timings. The odd shape can

be attributed to thread saturation at 7x7 matrix; all larger

matrix sizes show the original growth pattern resuming

(O(|V |

), r was held constant at 5).

ﬁt asymptotic runtime, assuming said algorithm does

not result in undue ciphertext bootstrapping.

5.2 HE Directed Triangle Counting

Triangle counting in all forms scales with O(V

) lin-

ear time. Triangle counting of all forms takes ad-

vantage of parallelism with O(V ) threads, reducing

time to O(V

) when O(V ) processors are available. In

all forms, triangle counting is time-invariant with the

number of triangles in the graph, scaling only with the

number of vertices.

5.3 HE Weighted Triangle-Creation

Scoring

We benchmark the query shown in Figure 1 over HE

graph data. This means that unlike the example, the

edges are encrypted and unknown to the cooperative.

In our tests, we hold the number of locations and ac-

tivities/hobbies constant and vary the number of peo-

ple. Realistically, the number of locations will gen-

erally not change given a constant service area for

the data cooperative. Further, the number of activi-

ties/hobbies available for people to do does not vary

with population, so it too is held constant.

Let |P| be the number of people, and let P ⊂

V . With O(|P|) parallelism available, HE weighted

triangle-creation scoring runtime grows at O(|P|)

when sparsity is held constant at 75% (25% of pos-

sible edges exist). Single-thread growth complexity

for this scoring method would be O(|P|

), as we have

near-perfect multithreaded speedup with each vertex

score being calculated independently.

6 CONCLUSION

In this paper, we discuss the fact that data coopera-

tives will, by nature of respecting participants will-

ingness to share data, be forced to work with incom-

plete data. We demonstrate and analyze algorithms

SECRYPT 2023 - 20th International Conference on Security and Cryptography

882

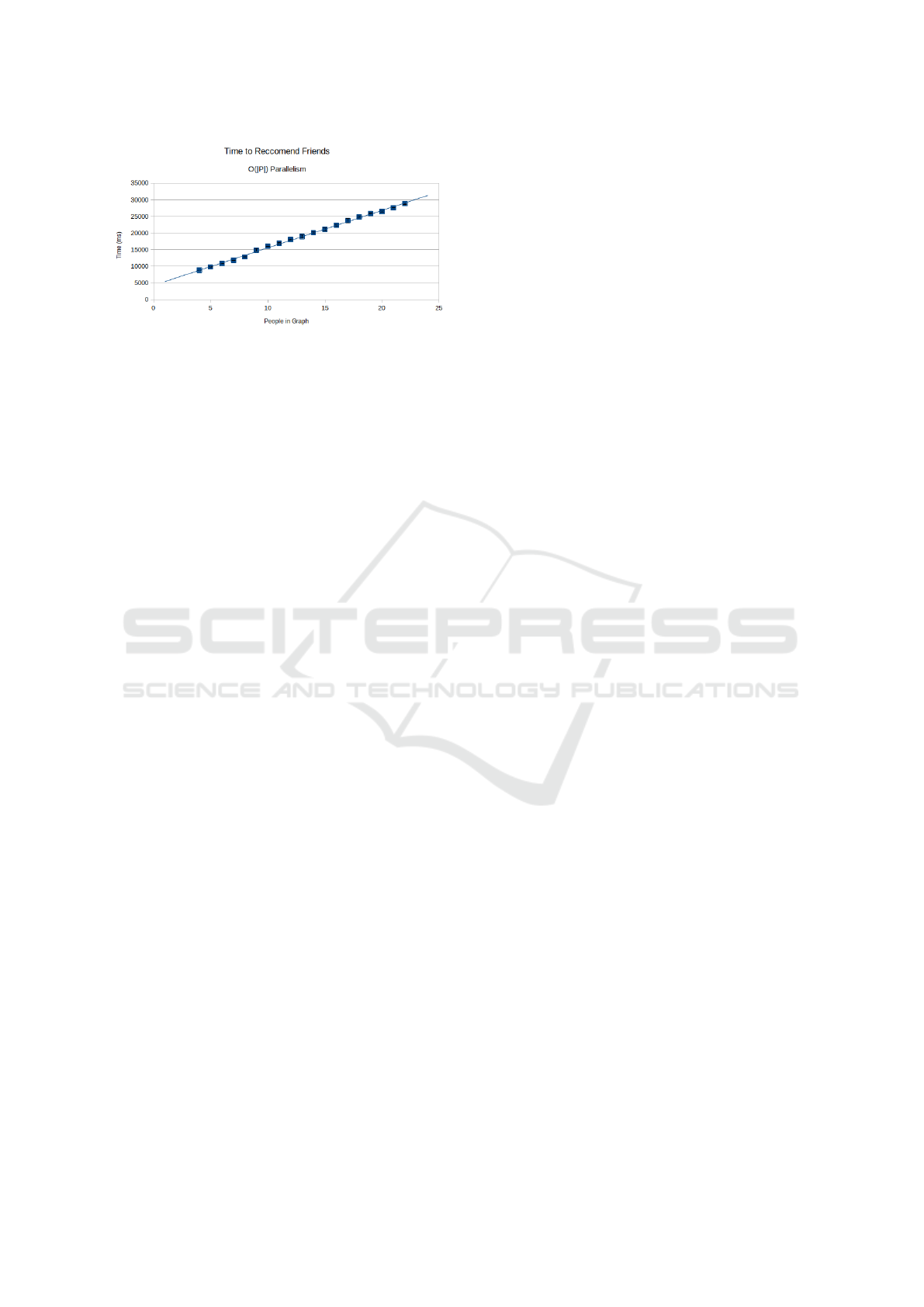
Figure 5: Time (in ms) to complete HE weighted triangle-

creation vertex scoring for the aforementioned friend rec-

ommendation vs number of people in the graph. With

O(|P|) parallelism, and constant sparsity in the graph, the

runtime is O(|P|).

for label propagation and directed triangle counting

over HE graph data. We also provide an example of

weighted triangle-creation scoring, a vertex scoring

scheme effective over HE heterogeneous graphs.

HE label propagation allows the data cooperative

to infer labels for data that is unlabeled, thereby cre-

ating a complete, but inferred, set of labels from a

set of encrypted labels. We demonstrate HE label

propagation in O(r ∗ S(|V |)) runtime, where S(|V |) is

the time complexity of squaring a |V | by |V | matrix,

and O(|V |

) space. Our benchmarked implementation

uses a parallel naive matrix multiply as the squaring

algorithm, resulting in O(r ∗ |V |

) runtime. There is

room for improvement on this front with a more efﬁ-

cient matrix squaring algorithm, so long as the algo-

rithm does not require an asymptotically larger num-

ber of ciphertext bootstrappings.

We expand the deﬁnition of a graph triangle to di-

rected graphs, and demonstrate triangle counting al-

gorithms for various forms of directed triangles over

HE directed graph data. These HE directed triangle

counting algorithms share an O(max(degree(V ))

)

runtime with up to O(|V |) parallelism.

Finally, we explore and benchmark HE weighted

triangle-creation scoring. This allows data coopera-

tives to generate vertex scores while strictly using HE

graph data in O(|V |) runtime given O(|V |) (or possi-

bly less) parallelism. The applications of this vertex-

scoring scheme go beyond the demonstrated hetero-

geneous social network friend recommendations: it

can be applied to network security, risk management,

and much more.

6.1 Future Work

Improvements to all of these can potentially be made

by utilizing CHIMERA (Boura et al., 2020) bridges.

Label propagation can be improved by bridging to

BFV or HEAAN/CKKS after the inversion step of

assembling the A matrix, with matrix squaring being

done in BFV or HEAAN/CKKS. Triangle counting

could potentially be improved by bridging to BFV af-

ter the binary logic and prior to the addition steps.

Although, this assumes the conversion will take

asymptotically less time than keeping the ciphertexts

in TFHE-mode. This is likely to be the case for label

propagation, but could offer questionable speedup for

triangle counting.

ACKNOWLEDGEMENTS

We sincerely acknowledge and thank the National

Centers of Academic Excellence in Cybersecurity,

housed in the Division of Cybersecurity Educa-

tion, Innovation and Outreach, at the National Secu-

rity Agency (NSA) for partially supporting our re-

search through grants H98230-20-1-0329, H98230-

20-1-0414, H98230-21-1-0262, H98230-21-1-0262,

and H98230-22-1-0329.

REFERENCES

Albrecht, M., Chase, M., Chen, H., Ding, J., Goldwasser,

S., Gorbunov, S., Halevi, S., Hoffstein, J., Laine,

K., Lauter, K., Lokam, S., Micciancio, D., Moody,

D., Morrison, T., Sahai, A., and Vaikuntanathan,

V. (2018). Homomorphic encryption security stan-

dard. Technical report, HomomorphicEncryption.org,

Toronto, Canada.

Boura, C., Gama, N., Georgieva, M., and Jetchev, D.

(2020). Chimera: Combining ring-lwe-based fully ho-

momorphic encryption schemes. Journal of Mathe-

matical Cryptology, 14(1):316–338.

Chen, H., Chillotti, I., and Song, Y. (2019). Multi-key ho-

momorphic encryption from tfhe. In Galbraith, S. D.

and Moriai, S., editors, Advances in Cryptology – ASI-

ACRYPT 2019, pages 446–472, Cham. Springer Inter-

national Publishing.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-

momorphic encryption for arithmetic of approximate

numbers. In Takagi, T. and Peyrin, T., editors, Ad-

vances in Cryptology – ASIACRYPT 2017, pages 409–

437, Cham. Springer International Publishing.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene, M.

(August 2016). TFHE: Fast fully homomorphic en-

cryption library. https://tfhe.github.io/tfhe/.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene, M.

(2019). Tfhe: Fast fully homomorphic encryption

over the torus. Journal of Cryptology.

Do, H. G. and Ng, W. K. (2016). Privacy-preserving tri-

angle counting in distributed graphs. In 2016 IEEE

30th International Conference on Advanced Informa-

tion Networking and Applications (AINA), pages 917–

924.

Privacy-Preserving Algorithms for Data Cooperatives with Directed Graphs

883

Dockendorf, M. and Dantu, R. (2023). Heterogeneous

graph storage and leakage prevention for data coop-

eratives. In International Conference on Security and

Cryptography.

Dockendorf., M., Dantu., R., and Long., J. (2022). Graph

algorithms over homomorphic encryption for data

cooperatives. In Proceedings of the 19th Interna-

tional Conference on Security and Cryptography - SE-

CRYPT,, pages 205–214. INSTICC, SciTePress.

Dockendorf, M., Dantu, R., Morozov, K., and Bhowmick,

S. (2021). Investing data with untrusted parties us-

ing he. In International Conference on Security and

Cryptography.

Fan, J. and Vercauteren, F. (2012). Somewhat practical fully

homomorphic encryption. Cryptology ePrint Archive,

Paper 2012/144. https://eprint.iacr.org/2012/144.

GDMA and Acxiom (2022). Us data privacy: What the

consumer really thinks. https://globaldma.com/wp-

content/uploads/2022/03/GDMA-US-Data-Privacy-

2022.pdf.

Holland, P. W. and Leinhardt, S. (1971). Transitivity

in structural models of small groups. Comparative

Group Studies, 2(2):107–124.

Li, X., Liu, S., Li, Z., Han, X., Shi, C., Hooi, B., Huang, H.,

and Cheng, X. (2020). Flowscope: Spotting money

laundering based on graphs. In AAAI.

Lindemann, N. (2023). What’s the average survey response

rate? [2021 benchmark].

opez-Alt, A., Tromer, E., and Vaikuntanathan, V. (2017).

Multikey fully homomorphic encryption and applica-

tions. SIAM Journal on Computing, 46(6):1827–1892.

Nayak, M. and Narayan, K. (2019). Strengths and weak-

nesses of online surveys. Technology, 6(7):0837–

2405053138.

Pentland, A. and Hardjono, T. (2020).

2. Data Cooperatives. 0 edition.

https://wip.mitpress.mit.edu/pub/pnxgvubq.

Pitas, I. (2016). Graph-based social media analysis, vol-

ume 39. CRC Press.

Raghavan, U. N., Albert, R., and Kumara, S. (2007). Near

linear time algorithm to detect community structures

in large-scale networks. Phys. Rev. E, 76:036106.

Robinson, I., Webber, J., and Eifrem, E. (2015). Graph

databases: new opportunities for connected data. ”

O’Reilly Media, Inc.”.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ‘small-world’ networks. nature, 393(6684):440–

442.

Wu, Y. and Chen, L. (2023). Structured encryption for trian-

gle counting on graph data. Future Generation Com-

puter Systems, 145:200–210.

Xie, P. and Xing, E. P. (2014). Cryptgraph: Privacy pre-

serving graph analytics on encrypted graph. CoRR,

abs/1409.5021.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

884