Measuring and Ranking Bipolarity via Orthopairs
Zolt
´
an Ern
˝
o Csajb
´
ok
a
Department of Health informatics, Faculty of Health Sciences, University of Debrecen
Sostoi ut 2-4, HU-4406 Nyıregyhaza, Hungary
Keywords:
Bipolarity, Orthopairs, Rough Set Theory, Interval Arithmetic, Measuring, Ranking.
Abstract:
Orthopairs, i.e., disjoint sets, are reasonable means to represent bipolar information. Bipolarity has different
models; we use the well-known Dubois-Prade typology. Of course, bipolarity can also carry uncertainty. In
this paper, we investigate mainly the bipolarity of type II. In Pawlak’s rough set theory, this bipolarity type,
with its uncertainty, can be modeled naturally. The “positive” and “negative” sets form an orthopair whose two
sets can be approximated by rough sets separately. Rough sets represented by nested sets can be considered
an interval set structure. With the help of counting measure, interval numbers can be assigned to the nested
sets. Then, relying on interval arithmetic, taking into account the uncertain nature of bipolarity, the degree of
bipolarity can be measured, and the positive and negative sets ranked.
1 INTRODUCTION
As Cacioppo, Gardner, and Berntson say in their sem-
inal paper (Cacioppo et al., 1997),
To be sure, there are in fact bipolarities and
dichotomies in the world. (p. 6)
Indeed, bipolarity can be found in many natural and
social science fields, even as a feature of human think-
ing.
Two sides of bipolar information are usually pro-
vided with positive and negative labels. “Positive”
and “negative” claim nothing else that the two sides
are well separated; nevertheless, they cannot com-
pletely be unrelated (Dubois and Prade, 2006). Bipo-
larity may also carry uncertainty.
Orthopair and its different generalizations are rea-
sonable means to represent bipolar information. Of
course, bipolarity may carry uncertainty as well.
Bipolarity arises naturally in Pawlak’s rough set
theory (Pawlak, 1982; Pawlak, 1991; Pawlak and
Skowron, 2007).
According to the Dubois and Prade typology
(Dubois and Prade, 2006; Dubois and Prade, 2008),
orthopair modeling of “Type II: Symmetric bivari-
ate bipolarity” can be interpreted naturally within the
rough set theory (see, also (Ciucci, 2011)).
In Pawlak’s rough set theory, rough sets repre-
sented by nested sets can be considered an interval set
a
https://orcid.org/0000-0002-6357-0233
structure to represent nonnumeric uncertainty on the
model of real interval numbers (Wong et al., 2013;
Yao, 2009; Yao and Wong, 1997; Yao and Li, 1996).
Then, with the help of counting measure, interval
numbers can be assigned to rough sets represented by
nested sets. With these interval numbers, the “size”
of bipolarity can be measured with different methods,
considering its uncertain nature.
In medical practice, it is often the case that one
or more diseases have almost identical clinical symp-
toms. Examples include the common cold and flu.
Likewise, the symptoms of hypothyroidism (caused
by an ”underactive” thyroid gland) and hyperthy-
roidism (caused by an ”overactive” thyroid gland) are
also closely related.
The general practitioner (GP) makes a presump-
tive diagnosis based on the clinical symptoms and
then refers the patient to a specialist. In this paper,
we focus on a possible numerical analysis of the pre-
sumptive diagnoses. It is important to consider the
two presumptive diagnoses, how much they differ,
and how ”stronger” one is than the other.
A set of patients based on two different diagnoses
can be divided into two mutually exclusive sets, i.e.,
they form an orthopair. Then, a numerical compar-
ison of the two presumptive diagnoses can be made
using the proposed calculations. It relies on the com-
bination of rough set theory and interval arithmetic.
In Section 2, basic notations and notions of rough
sets are summarized. Section 3 and Section 4
338
Csajbók, Z.
Measuring and Ranking Bipolarity via Orthopairs.
DOI: 10.5220/0012180800003595
In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 338-347
ISBN: 978-989-758-674-3; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

overview different representations of rough sets and
the basic facts about interval arithmetic. Section 5
presents the typology of bipolarity; the modeling and
measuring of the bipolarity of Type II; the ranking of
positive and negative reference sets; and the model-
ing of the bipolarity of Type III. Section 6 gives an
illustrative example.
2 BASIC NOTATIONS
Let U and V be two nonempty sets.
A function f is denoted by f : U → V , u 7→ f (u)
with domain U and codomain V ; u 7→ f (u) is the as-
signment or mapping rule of f . V
U
denotes the set of
all functions from U into V .
For any S ⊆ U, f (S) = { f (u) | u ∈ S} ⊆ V is the
direct image of S. f (U ) is the range of f .
Let S ⊆ U . S
c
is the complement of S with respect
to U. If f ∈ V
U
, the complement of f (S) with respect
to V is denoted by f
c
(S) instead of ( f (S))
c
.
P (U) is the set of subsets of U, that is the power
set of U.
Let R represent the real numbers.
The sets S
1
and S
2
(S
1
,S
2
∈ P (U)) are commonly
called disjoint if S
1
∩ S
2
=
/
0. The family S of sets is
called disjoint if any two distinct sets in S are disjoint.
In this case, ∪S is referred to as a disjoint union and
specially denoted by ⊎S .
If a,b ∈ R and a ≤ b, [a,b] = {x ∈ R | a ≤ x ≤ b}
and ]a,b[ = {x ∈ R | a < x < b} denote closed and
open intervals. It is easy to interpret the open-closed
]a,b] and closed-open [a,b[ intervals.
(·,·) denotes an ordered pair.
| · | is the cardinality of a set.
3 ROUGH SETS
Let U be a nonempty set.
PAS (U) = (U,B,D
B
,ℓ, u) is a Pawlak’s approxi-
mation space if
• B = Π (U) is a partition of U; its equivalence
classes are called base sets.
• D
B
is defined with the following inductive defini-
tion:
–
/
0 ∈ D
B
, B ⊆ D
B
;
– if D
1
,D
2
∈ D
B
, then D
1
∪ D
2
∈ D
B
.
The members of D
B
are called definable sets.
• Lower and upper approximation operators ℓ and
u are defined as
– ℓ : P (U) → D
B
, S 7→ ∪{B ∈ B | B ⊆ S};
– u : P (U) → D
B
, S 7→ ∪{B ∈ B | B ∩ S ̸=
/
0}.
The boundary operator derived from lower and
upper operators is also defined on P (U):
bnd : P (U) → D
B
,S 7→ u(S) \ ℓ(S).
It is easy to check that bnd(S) is definable indeed.
It is straightforward that u(S) = ℓ(S) ⊎ bnd(S).
The sets in Pawlak’s approximation spaces are
characterized with the following notions. A set S ∈
P (U) is
• crisp (exact) if ℓ(S) =u(S), i.e., bnd(S)=
/
0;
• rough (inexact) if it is not exact, i.e., bnd(S) ̸=
/
0.
An important feature of Pawlak’s approximation
spaces is that the exactness and definability coincide.
Therefore these two terms can be used synonymously.
For each S ∈ P (U ), the lower and upper approx-
imation pair (ℓ,u) divides the universe U into three
mutual disjoint regions:
• POS(S) = ℓ(S) — positive region of S;
if u ∈ POS(S), it is said that u is an positive exam-
ple of S.
• NEG(S)=U \ u(S)=u
c
(S) — negative region of S;
if u ∈ NEG(S), it is said that u is a negative exam-
ple of S.
• BN(S) = bnd(S) — borderline region of S;
if u ∈ BN(S), it is said that u is an abstained ex-
ample of S.
Knowledge of algebraic aspects of rough sets was
summarized by Banerjee and Chakraborty in their
comprehensive study (Banerjee and Chakraborty,
2004). From now on, especially different definitions
of rough sets and partly their formalism are based on
(Banerjee and Chakraborty, 2004).
Let PAS(U) = (U,B,D
B
,ℓ, u) be a finite Pawlak
approximation space.
Let S
1
,S
2
∈ P (U ). It is said that S
1
and S
2
are
roughly equal, in notation S
1
≈ S
2
, if l(S
1
) = l(S
2
)
and u(S
1
) = u(S
2
). It is straightforward that ≈ is an
equivalence relation on P (U). Then the rough sets
are the equivalence classes of P (U)/ ≈.
For the detailed structure of P (U)/ ≈, see (Baner-
jee and Chakraborty, 2004; Bonikowski, 1992). Here
we present below its most relevant properties for this
paper.
The equivalent class containing S ∈ P (U) is de-
noted by JSK. By definition, for all S
′
∈ JSK, S
′
≈ S,
i.e., ℓ(S
′
) = ℓ(S) and u(S
′
) = u(S), consequently
ℓ(S) ⊆ S
′
⊆ u(S).
A set S ∈ P (U) may be exact or rough. Let us see
what happens in these two cases.
Measuring and Ranking Bipolarity via Orthopairs
339

1. S is exact.
Clearly, S is exact if and only if |JSK| = 1 and
JSK = {S}. Moreover, ℓ(S) = S = u(S) ∈ JSK.
2. S is rough.
If S is rough, i.e., ℓ(S) ̸= u(S), then S ∈ JSK by
definition, but
• ℓ(S) ̸∈ JSK, because ℓ(ℓ(S)) = ℓ(S), but
u(ℓ(S)) = ℓ(S) ̸= u(S);
• u(S) ̸∈ JSK, because ℓ(u(S)) = u(S) ̸= ℓ(S),
though u(u(S)) = u(S).
In sum, if S ∈ P (U) is rough, for all S
′
∈ JSK,
ℓ(S) ⊊ S
′
⊊ u(S).
Remark 1. It is worth paying attention to the terms
that have evolved historically. A set is rough if its
boundary is not the empty set. A rough set is an equiv-
alence class from P (U)/ ≈. □
There are additional equivalent representations of
rough sets; namely, for each S ∈ P (U),
(1) JSK ∈ P (U)/ ≈,
(2) (ℓ(S), u(S)),
(3) (ℓ(S), u
c
(S)),
(4) (ℓ(S), bnd(S)).
are rough sets. These four definitions are equiva-
lent to each other in the sense that for any S ∈ P (U )
the equivalent class JSK in P (U)/ ≈, and the enti-
ties (ℓ(S),u(S)), (ℓ(S), u
c
(S)), and (ℓ(S),bnd(S)) are
identifiable ((Banerjee and Chakraborty, 2004), pp.
158-159).
By definition, ℓ(S) ∩ u
c
(S) =
/
0 and ℓ(S) ∩
bnd(S) =
/
0 hold in the cases of representations (2)
and (3). That is, in these approaches, orthopairs
represent rough sets. However, for our purposes,
choosing (2) will be appropriate. In this case, rough
sets are represented by nested pairs of sets. However,
not every pair (S
1
,S
2
) (S
1
,S
2
,∈ P (U),S
1
⊆ S
2
) forms
a rough set.
Proposition 1. Let S
1
,S
2
,∈ P (U), S
1
⊆ S
2
. The pair
(S
1
,S
2
) is a rough set of the form (ℓ(S),u(S)) for a set
S (S
1
⊆ S ⊆ S
2
) if and only if S
1
and S
2
are definable
and S
2
\ S
1
does not contain any singleton base set.
Proof. See, (Marek and Truszczy
´
nski, 1999), Propo-
sition 3.2. □
4 BASIC NOTIONS OF INTERVAL
ARITHMETIC
In this section, basic definitions, notations, facts, and
partly their formalism concerning interval numbers
are based mainly on (Moore et al., 2009), and partly
on (Alefeld and Mayer, 2000; Hickey et al., 2001;
Sengupta and Pal, 2000).
An interval number or interval is simply a closed
real interval of the form
a = [a
l
,a
u
] = {x ∈ R | a
l
≤ x ≤ a
u
},
where a
l
and a
u
denote the left and right endpoints of
the interval a, respectively.
If a
l
= a
u
, i.e., the interval a is degenerate, and it
is identified with the real number a = a
l
= a
u
.
Some frequently used special terms for an interval
number a are the following.
• m(a) =
1
2
(a
l
+ a
u
) is the midpoint or center of a;
• w(a) = a
u
− a
l
is the width or diameter of a.
Two intervals a = [a
l
,a
u
] and b = [b
l
,b
u
] are said
to be equal, in notation a = b, if a
l
= b
l
and a
u
= b
u
.
Let ⊙ ∈ {+,−,·,/} be a binary operation of the
four elementary binary operations on R, i.e., addition,
subtraction, multiplication, and division, respectively.
Then the following general formula
a ⊙ b = {x ⊙ y | x ∈ a, y ∈ b}
defines four binary operations on the set of interval
numbers. Their endpoint formulas are the following
(Moore et al., 2009):
a + b = [a
l
+ b
l
,a
u
+ b
u
]
a − b = a + (−b) = [a
l
− b
u
,a
u
− b
l
],
where − b = [−b
u
,−b
l
]
a · b = [min{a
l
b
l
,a
l
b
u
,a
u
b
l
,a
u
b
u
},
max{a
l
b
l
,a
l
b
u
,a
u
b
l
,a
u
b
u
}]
a/b = a · (1/b),
where 1/b = [1/b
u
,1/b
l
] (0 /∈ b).
For nonnegative intervals a and b (0 ≤ a
l
≤ a
u
,
0 ≤ b
l
≤ b
u
), formulae for multiplication and division
are simplified to:
• a · b = [a
l
b
l
,a
u
b
u
];
• a/b = [a
l
/b
u
,a
u
/b
l
],
provided in addition that 0 < b
l
.
Let λ ∈ R be a real number. Then, multiplication
with a scalar λ can be defined as a special case of the
multiplication: λ · a = λ[a
l
,a
u
] = [λ,λ] · [a
l
,a
u
].
5 MAIN RESULTS: MODELING
AND MEASURING OF
BIPOLARITY
Orthopair and its different generalizations are rea-
sonable means to represent bipolar information, and
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
340

they are widely used to model uncertainty (Cam-
pagner and Ciucci, 2017; Ciucci, 2011; Marek and
Truszczy
´
nski, 1999; Yager and Alajlan, 2017). On the
other hand, in rough set theory, bipolarity arises natu-
rally: positive/negative, positive/boundary, and nega-
tive/boundary regions.
For a comprehensive discussion of orthopairs,
their generalizations, and their connection with rough
sets, see (Ciucci, 2011; Gehrke and Walker, 1992;
Marek and Truszczy
´
nski, 1999; Pagliani, 1998), and
the references therein.
5.1 Typology of Bipolarity
Two sides of bipolar information are called positive
and negative aspects. “Positive” and “negative” just
mean that the two sides are separated in one way or
another. Nevertheless, they cannot be completely un-
related, additional relationships between them may be
supposed as well (Dubois and Prade, 2006).
Bipolarity has several forms depending on the
nature of the link between its two sides. Dubois
and Prade gave the typology of the following forms
(Dubois and Prade, 2006; Dubois and Prade, 2009).
Representation of bipolarity relies on some char-
acteristics (data, information, opinion, response) of
entities (objects, persons, notions).
Bipolarity of Type I Symmetric (homogeneous)
univariate bipolarity:
• the evaluation is either totally positive or totally
negative;
• positive and negative aspects are mutually ex-
clusive and evaluated simultaneously;
• the evaluation relies on same data.
This is the most constrained form.
Bipolarity of Type II Symmetric (homogeneous)
bivariate bipolarity:
• the evaluation is not necessarily totally positive
nor totally negative;
• positive and negative aspects have a duality re-
lation, and they are evaluated separately;
• the evaluation relies on the basis of the same
data.
This is a looser form.
Bipolarity of Type III Asymmetric (heterogeneous)
bivariate bipolarity:
• the evaluation is neither totally positive nor to-
tally negative;
• positive and negative aspects are evaluated sep-
arately, a duality relation between them is not
required;
• the evaluation does not rely on the same data.
This is the loosest form.
5.2 Modeling and Measuring of
Bipolarity of Type II
Bipolarity of type II can be modeled with Pawlak’s
approximation spaces within rough set theory in an
appropriate manner.
Let PAS (U) = (U,B,D
B
,ℓ, u) be a finite
Pawlak’s approximation space.
Let ⟨A
+
,A
−
⟩, be an orthopair, viz. A
+
,A
−
∈ P (U )
and A
+
∩ A
−
=
/
0. A
+
and A
−
are called the positive
reference set and negative reference set, respectively.
Based on A
+
and A
−
as two separate entities, let
us form two distinct rough sets in their own right. Let
us choose the nested pair rough set representation:
RS
A
+
= (ℓ(A
+
),u(A
+
)) and RS
A
−
= (ℓ(A
−
),u(A
−
)).
Measure is a mathematical device which reflects
some sorts of “size” of sets. The simple so-called
counting measure accounts for the size of sets as the
number of their elements. It plays a key role in rough
set theory.
Applying counting measure, interval numbers can
be assigned to the former rough sets:
RS
A
+
7→ [|ℓ(A
+
)|,|u(A
+
)|] = a
+
= [A
ℓ
+
,A
u
+
]
and
RS
A
−
7→ [|ℓ(A
−
)|,|u(A
−
)|] = a
−
= [A
ℓ
−
,A
u
−
]
In the above formulae, to avoid heavy nota-
tions, the simplified symbols A
l
+
, A
u
+
, and A
bnd
+
have
been introduced instead of |ℓ(A
+
)|, |u(A
+
)|, and
|bnd(A
+
)|. Similar notations have been introduced
for A
−
as well. In addition, the intervals [A
ℓ
+
,A
u
+
] and
[A
ℓ
−
,A
u
−
] have been denoted by a
+
and a
−
.
Many diverse methods have been proposed
to compare interval numbers, for their historical
overview, see, (Xu and Chen, 2008). For the com-
parison between two interval numbers, Facchinetti
et al. (Facchinetti et al., 1998), Xu and Da (Xu
and L. Da, 2002), and Wang et al. (Wang et al.,
2005) have been, respectively, proposed three so-
called possibility-degree formulae. It turned out that
these three formulae are equivalent ((Xu and Chen,
2008), Theorem 2). This paper will use the formula
proposed by Xu and Da in (Xu and L. Da, 2002)
because it is the most appropriate for our purposes.
Definition 1 ((Xu and L. Da, 2002), Definition 2.3).
Let a = [a
l
,a
u
] and b = [b
l
,b
u
] be two real interval
numbers. The possibility degree of a over b, in
Measuring and Ranking Bipolarity via Orthopairs
341

notation p(a ≥ b), is defined by
p(a ≥ b)
= max

1 − max

b
u
− a
l
(a
u
− a
l
) + (b
u
− b
l
)
,0

,0

= max

1 − max

b
u
− a
l
w(a) + w(b)
,0

,0

(1)
Similar formula is defined for the possibility degree
of b over a by
p(b ≥ a)
= max

1 − max

a
u
− b
l
(a
u
− a
l
) + (b
u
− b
l
)
,0

,0

= max

1 − max

a
u
− b
l
w(a) + w(b)
,0

,0

(2)
□
The following theorem summarises the most im-
portant properties of the possibility degree just de-
fined.
Theorem 1 ((Xu and L. Da, 2002), Theorem 2.1).
Let a = [a
l
,a
u
] and b = [b
l
,b
u
] be two real interval
numbers. The following properties for the possibility
degree of a over b (b over a) hold:
1. 0 ≤ p(a ≥ b) ≤ 1,
0 ≤ p(b ≥ a) ≤ 1.
2. p(a ≥ b) + p(b ≥ a) = 1
3. p(a ≥ b) = 1 if and only if b
u
≤ a
l
,
p(b ≥ a) = 1 if and only if a
u
≤ b
l
.
4. p(a ≥ b) = 0 if and only if a
u
≤ b
l
,
p(b ≥ a) = 0 if and only if b
u
≤ a
l
.
5. p(a ≥ a) =
1
2
.
6. p(a ≥ b) ≥
1
2
if and only if a
u
+ a
l
≥ b
u
+ b
l
.
Especially, p(a ≥ b) =
1
2
if and only if a
u
+ a
l
=
b
u
+ b
l
.
Properties (3) and (4) mean that the possibility de-
gree of a over b are equal to 0 or 1 if and only if they
do not have a common area regardless of the distance
between a and b. Similar property holds for the pos-
sibility degree of b over a.
Let us consider the possibility degree of reference
sets over each other.
Possibility degree of the positive reference over
negative reference set and the negative reference set
over positive reference set can be calculated. With
the above notations:
p(a
+
≥ a
−
) and p(a
−
≥ a
+
).
Proposition 2. Let PAS(U) be a Pawlak’s approxi-
mation space and (A
+
,A
−
) be an orthopair. Then
1. p(a
+
≥ a
−
) = 1 if and only if |u(A
−
)| ≤ |ℓ(A
+
)|.
2. p(a
+
≥ a
−
) = 0 if and only if |u(A
+
)| ≤ |ℓ(A
−
)|.
Proof.
p(a
+
≥ a
−
) = p([A
ℓ
+
,A
u
+
] ≥ [A
ℓ
−
,A
u
−
])
= p([|ℓ(A
+
)|,|u(A
+
)|]
≥ [|ℓ(A
−
)|,|u(A
−
)|])
Hence, statements 1. and 2. follow from Theorem
1/3, and Theorem 1/4, respectively. □
The statement
p(a
+
≥ a
−
) = 1 if and only if |u(A
−
)| ≤ |ℓ(A
+
)|
means that the possibility degree of the positive refer-
ence set A
+
over negative reference set A
−
is equal to
1 if and only if the cardinality of the upper approxi-
mation of the negative reference set u(A
−
) is less than
or equal to the cardinality of the lower approximation
of the positive reference set ℓ(A
+
).
The statement
p(a
+
≥ a
−
) = 0 if and only if |u(A
+
)| ≤ |ℓ(A
−
)|
means that the possibility degree of the positive refer-
ence set A
+
over negative reference set A
−
is equal to
0 if and only if the cardinality of the upper approxi-
mation of the positive reference set u(A
+
) is less than
or equal to the cardinality of the lower approximation
of the negative reference set ℓ(A
−
).
Proposition 3. Let PAS(U) be a Pawlak’s approxi-
mation space and (A
+
,A
−
) be an orthopair. Then
p(a
+
≥ a
−
) =
1
2
if and only if
|u(A
+
)| − |u(A
−
)| = |ℓ(A
−
)| − |ℓ(A
+
)|.
Proof.
p(a
+
≥ a
−
) = p([A
ℓ
+
,A
u
+
] ≥ [A
ℓ
−
,A
u
−
])
= p([|ℓ(A
+
)|,|u(A
+
)|]
≥ [|ℓ(A
−
)|,|u(A
−
)|]) =
1
2
by Theorem 1/6
⇔ |u(A
+
)| + |ℓ(A
+
)| = |u(A
−
)| + |ℓ(A
−
)|
⇔ |u(A
+
)| − |u(A
−
)| = |ℓ(A
−
)| − |ℓ(A
+
)|
□
Let |u(A
+
)| − |u(A
−
)| = |ℓ(A
−
)| − |ℓ(A
+
)| = K.
Then p(a
+
≥ a
−
) =
1
2
can be interpreted in the
following way:
The possibility degree of the positive reference set
over the negative reference set is equal to
1
2
if
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
342

• provided K = 0:
– The elements of lower approximations of posi-
tive and negative reference sets are equal;
– and the elements of upper approximations of
positive and negative reference sets are also
equal at the same time.
• provided K > 0:
– The upper approximation of the positive ref-
erence set as much many more elements than
the elements of the upper approximation of the
negative reference set
– as the elements of the lower approximation of
the negative reference set has more elements
than the elements of the lower approximation
of the positive reference set.
• provided K < 0: The interpretation in this case can
be done in a similar way as in case K > 0.
The above interpretations are reasonable, and co-
incide with our intuitive approach.
5.3 Ranking of Positive and Negative
Reference Sets
To rank the positive and negative reference sets, both
of them must be compared with themselves and one
with the other. Specifically, the following quantities
must be formed (Xu and L. Da, 2002):
p(a
+
≥ a
+
), p(a
+
≥ a
−
),
p(a
−
≥ a
+
), p(a
−
≥ a
−
).
where
• p(a
+
≥ a
+
), p(a
+
≥ a
−
), p(a
−
≥ a
+
), p(a
−
≥
a
−
) ≥ 0;
• p(a
+
≥ a
+
) = p(a
−
≥ a
−
) =
1
2
(Theorem 1, 5.);
• p = (a
+
≥ a
−
)+ p(a
−
≥ a
+
) = 1 (Theorem 1, 2.).
These quantities can be arranged in the matrix of
the form
P =

p(a
+
≥ a
+
) p(a
+
≥ a
−
)
p(a
−
≥ a
+
) p(a
−
≥ a
−
)

.
Let us sum these quantities lines by lines as fol-
lows:
p
+
= p(a
+
≥ a
+
) + p(a
+
≥ a
−
),
p
−
= p(a
−
≥ a
+
) + p(a
−
≥ a
−
).
Then the positive and negative reference sets can
be ranked in increasing or descending order according
to the quantities p
+
and p
−
naturally.
In (Wang et al., 2005) Wang et al. proposed an-
other ranking method for interval numbers.
Definition 2 ((Wang et al., 2005), Definition 2).
Let a = [a
l
,a
u
] and b = [b
l
,b
u
] be two real interval
numbers.
• If p(a ≥ b)>p(b ≥ a), it is said that a superior to b
to the degree of p(a ≥ b), in notation a ≻
p(a≥b)
b.
• If p(a ≥ b) = p(b ≥ a) =
1
2
, it is said that a is
indifferent to b, in notation a ∼ b.
• If p(b ≥ a)>p(a ≥ b), it is said that a is inferior to
b to the degree p(b ≥ a), in notation a ≺
p(b≥a)
b.
□
The matrix P can be applied to compare the posi-
tive and negative reference sets concerning Definition
2.
Definition 3. The positive reference set is
• superior to the negative reference set to the degree
p(a
+
≥ a
−
) if
a
+
≻
p(a
+
≥a
−
)
a
−
;
• indifferent to the negative reference set if
a
+
∼ a
−
;
• inferior to the negative reference set to the degree
p(a
−
≥ a
+
) if
a
−
≻
p(a
−
≥a
+
)
a
+
.
□
Remark 2. Roughly speaking,
• a
+
≻
p(a
+
≥a
−
)
a
−
means that the possibility degree
of the positive reference set over the negative ref-
erence set is greater than the possibility degree of
the negative reference set over the positive refer-
ence set to the degree p(a
+
≥ a
−
);
• a
+
∼ a
−
means that the possibility degree of the
positive reference set over the negative reference
set is equal to the possibility degree of the nega-
tive reference set over the positive reference set;
• a
−
≻
p(a
−
≥a
+
)
a
+
means that the possibility degree
of the negative reference set over the positive ref-
erence set is greater than the possibility degree of
the positive reference set over the negative refer-
ence set to the degree p(a
−
≥ a
+
). □
5.4 An Illustrative Example
In practice, the equivalence relation of objects comes
from the characteristics of objects. After Pawlak, ob-
jects and their attributes (characteristics) arranged in
a table is called the Information Table or Information
System (Pawlak, 1981; Pawlak, 1982; Ciucci, 2011).
Measuring and Ranking Bipolarity via Orthopairs
343

Definition 4 ((Pawlak, 1981), pp. 205-206). An
Information System is a structure IS = (U,A,V, F),
where
• U is a finite, nonempty set of objects;
• A is a finite, nonempty set of attributes;
• V = ∪
a∈A
V
a
, where V
a
is the set of all possible
values that can be observed for an attribute a ∈ A
concerning all objects from U;
• F is an information function F : U ×A → V , where
F assigns a value F(u,a) ∈ V to any pair (u, a)
(u ∈ U,a ∈ A).
If the function F is total, the system is called com-
plete, otherwise, it is incomplete. □
Due to the finiteness of the information system,
the information function can be given by a finite table.
The columns of the table are labeled with attributes,
and the rows with objects. Of course, the order of
columns and rows in the table is insignificant. In ad-
dition, some attributes can share a set of values.
Next, we define a binary relation on U.
Definition 5. Let B ⊆ A be a subset of attributes.
Two objects x,y ∈ U are called indiscernible with
respect to B, in notation xI
B
y, if F(x,a) = F(y,a)(a ∈
B). □
It is easy to check that the indiscernibility relation
I
B
is an equivalence one. The equivalence class con-
taining x is JxK
I
B
= {y ∈ U | xI
B
y}. The partition gen-
erated by I
B
is denoted by Π
B
, and the set of definable
sets is D
B
. Thus Pawlak’s approximation space is
PAS(U ) = (U,Π
B
,D
B
,ℓ
B
,u
B
).
Turning to the example, let us consider the symp-
toms of thyroid dysfunctions. We deal with only hy-
pothyroidism and hyperthyroidism thyroid disorders
(Ladenson and Kim, 2011).
An ”underactive” thyroid gland (which releases
too much hormone) causes the symptoms of hypothy-
roidism, and an ”overactive” thyroid gland (which
does not produce enough hormone) causes the symp-
toms of hyperthyroidism. Their clinical symptoms are
closely related.
Table 1, Information Table, summarizes some pa-
tients’ observed clinical symptoms concerning thy-
roid dysfunction. Expanding this table, the last two
columns, based on these clinical symptoms, con-
tain presumptive diagnoses made by a general prac-
titioner. A patient may develop a hypothyroidism or
hyperthyroidism thyroid disorder, perhaps neither of
them. The possible symptoms have been compiled
based on GP experiences but simplified here for illus-
trative purposes.
The set of objects, here patients, is:
U = {P
1
,P
2
,P
3
,P
4
,P
5
,P
6
,P
7
,P
8
,P
9
,P
10
}.
The possibly presumptive diagnoses are:
Hypothyroidism: yes, no, Hyperthyroidism:
yes, no.
The observed clinical symptoms are included in
the attribute set
A = {Weight change,Oedema,Tachycardia,
Increased sweating, Weakness,
Morbid psychomotor activity}. (3)
The possible values of the attributes are
• V
Weight change
= {loss,gain, unchanged}.
• V
Oedema
= {yes,no}.
• V
Tachycardia
= {yes,no}.
• V
Increased sweating
= {yes,no}.
• V
Weakness
= {yes,no}.
• V
Morbid psychomotor activity
= {excitement,slowness, unchanged}.
V =V
Weight change
∪V
Oedema
∪V
Tachycardia
∪V
Increased sweating
∪V
Weakness
∪V
Morbid psychomotor activity
= {loss,gain, unchanged,yes,no,
excitement,slowness}
Let S
hypo
(“positive reference set”) and S
hyper
(“negative reference set”) be the sets of patients who
demonstrably suffer from hypothyroidism and hyper-
thyroidism:
S
hypo
= {P
1
,P
2
,P
4
,P
7
,P
8
},S
hyper
= {P
3
,P
5
,P
6
,P
9
}.
The sets S
hypo
and S
hyper
form an orthopair because
S
hypo
∩ S
hyper
=
/
0.
Let choose the attribute set
B = {Weight change} ⊆ A.
Then the equivalence relation with respect to
B is I
B
with P
i
I
B
P
j
if F(P
i
,Weight change) =
F(P
j
,Weight change) (i, j = 1,2,.. .,10). Hence,
the partition of U generated by I
B
is
Π
B
= {{P
1
,P
6
,P
7
},{P
5
,P
9
},{P
2
,P
3
,P
4
,P
8
,P
10
}},
reflecting the weight change being “gain,” “loss,” and
“unchanged”, respectively.
Let consider RS
S
hypo
= (ℓ
B
(S
hypo
),u
B
(S
hypo
)).
ℓ
B
(S
hypo
) =
/
0,
u
B
(S
hypo
) = {P
1
,P
6
,P
7
} ∪ {P
2
,P
3
,P
4
,P
8
,P
10
}
= {P
1
,P
2
,P
3
,P
4
,P
6
,P
7
,P
8
,P
10
},
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
344

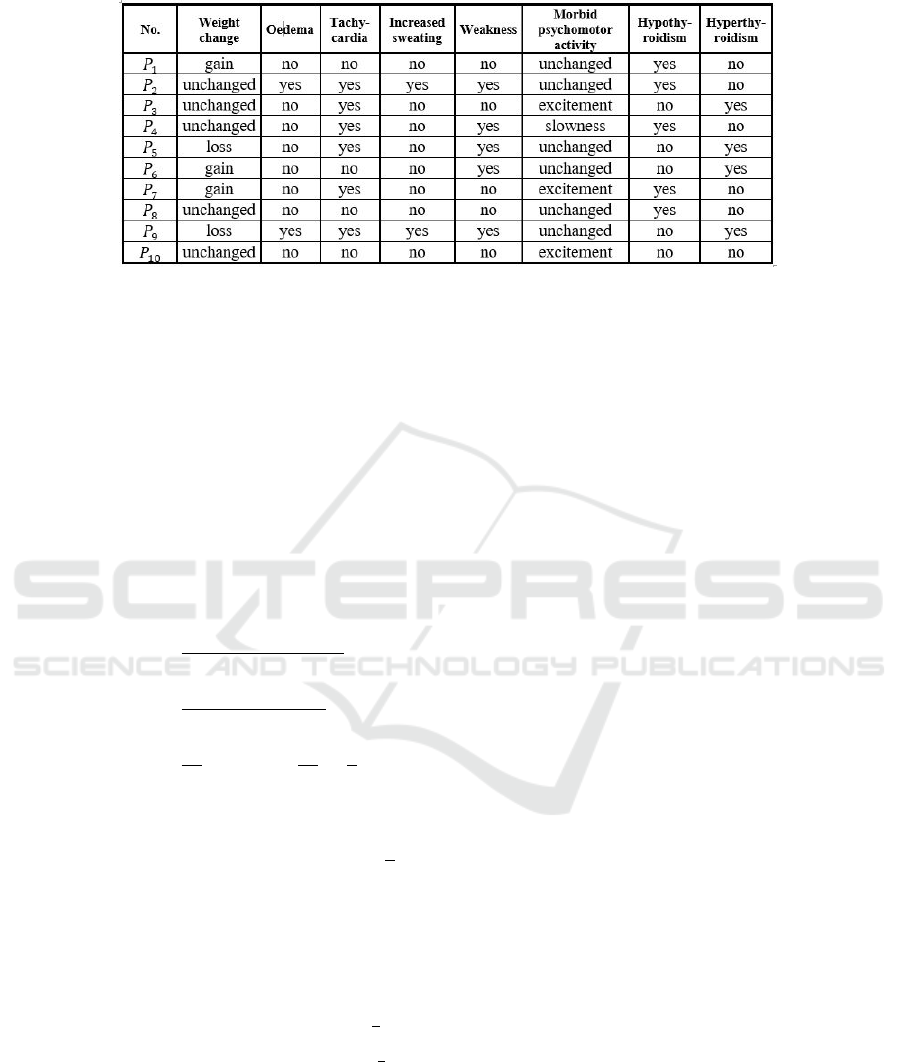
Table 1: Clinical symptoms of thyroid dysfunction and presumptive diagnoses.
Then,
a
hypo
= [a
l
,a
u
] = [|ℓ
B
(S
hypo
)|,|u
B
(S
hypo
)|] = [0,8].
Let consider RS
S
hyper
= (ℓ
B
(S
hyper
),u
B
(S
hyper
)).
ℓ
B
(S
hyper
) = {P
5
,P
9
},
u
B
(S
hyper
) = U.
Then,
b
hyper
= [b
l
,b
u
] = [|ℓ
B
(S
hyper
)|,|u
B
(S
hyper
)|] = [2,10].
With the Eqn. (1), we can calculate:
p(a
hypo
≥ b
hyper
)
= max

1 − max

b
u
− a
l
(a
u
− a
l
) + (b
u
− b
l
)
,0

,0

= max

1 − max

10 − 0
(8 − 0) + (10 − 2)
,0

,0

= max

1 − max

10
16
,0

,0

=
6
10
=
3
5
.
According to Theorem 1, Properties 2,
p(b
hyper
≥ a
hypo
) = 1 − p(a
hypo
≥ b
hyper
) =
2
5
.
These results can be interpreted as follows. With
respect to our knowledge represented in Table 1 and
partitioning U by Weight change, the overall contri-
bution of the clinical symptoms weight change to the
presence of
• hypothyroidism has the possibility degree
3
5
,
• hyperthyroidism has the possibility degree
2
5
.
It must be noted that, at this stage of the study,
this interpretation focuses purely on the mathematical
relationships without entering into medical issues.
5.5 Modeling Bipolarity of Type III
Type III bipolarity can be modeled by two distinct
general set approximation spaces over the same uni-
verse. Pawlak’s approximation space is a classical
one and has many generalizations. Here we only de-
scribe the generalisation that we need.
GAS(U) = (U,B ,D
B
,ℓ, u) is a finite general
approximation space if
• U is finite nonempty set;
• B is not a partition of U but covers it: ∪B = U;
• base system D
B
is strictly union type defined with
the following inductive definition:
–
/
0 ∈ D
B
, B ⊆ D
B
;
– if D
1
,D
2
∈ D
B
, then D
1
∪ D
2
∈ D
B
.
• Lower and upper approximation operators ℓ and u
are defined as
– ℓ : P (U) → D
B
, S 7→ ∪{B ∈ B | B ⊆ S};
– u : P (U) → D
B
, S 7→ ∪{B ∈ B | B ∩ S ̸=
/
0}.
To model Type III Bipolarity, let us define two dis-
tinct base systems for the independent description of
positive and negative reference sets on the universe
U. Applying the creation rules of GAS (U), we obtain
two approximation spaces with different structures:
• GAS
+
(U) =

U,B
+
,D
B
+
,ℓ
+
,u
+

,
• GAS
−
(U) =

U,B
−
,D
B
−
,ℓ
−
,u
−

.
The measuring and ranking of positive and nega-
tive reference sets can be done by accordingly mod-
ifying the general procedure in the two different
approximation spaces.
6 CONCLUSION
In this paper, measuring the extent of bipolarity has
been proposed with the help of interval arithmetic.
Measuring and Ranking Bipolarity via Orthopairs
345

Working in finite Pawlak approximation space, the
uncertain nature of bipolarity approximating the pos-
itive and negative reference sets with rough sets has
also been modeled. The proposed methods can be ex-
tended to any family of mutual disjoint sets.
ACKNOWLEDGEMENTS
The author would like to thank the anonymous
referees for their useful comments and suggestions.
REFERENCES
Alefeld, G. and Mayer, G. (2000). Interval analy-
sis: theory and applications. Journal of Compu-
tational and Applied Mathematics, 121(1):421–
464.
Banerjee, M. and Chakraborty, M. (2004). Alge-
bras from rough sets. In Pal, S., Polkowski, L.,
and Skowron, A., editors, Rough-Neuro Com-
puting: Techniques for Computing with Words,
pages 157–184. Springer.
Bonikowski, Z. (1992). A certain conception of the
calculus of rough sets. Notre Dame Journal of
Formal Logic, 33(3):412–421.
Cacioppo, J. T., Gardner, W. L., and Berntson, G. G.
(1997). Beyond bipolar conceptualizations and
measures: The case of attitudes and evaluative
space. Personality and Social Psychology Re-
view, 1(1):3–25.
Campagner, A. and Ciucci, D. (2017). Measuring
uncertainty in orthopairs. In Antonucci, A.,
Cholvy, L., and Papini, O., editors, Symbolic
and Quantitative Approaches to Reasoning with
Uncertainty - 14th European Conference, EC-
SQARU 2017, Lugano, Switzerland, July 10-
14, 2017, Proceedings, volume 10369 of LNCS,
pages 423–432. Springer.
Ciucci, D. (2011). Orthopairs: A simple and widely
used way to model uncertainty. Fundam. Inf.,
108(3-4):287–304.
Dubois, D. and Prade, H. (2006). Bipolar represen-
tations in reasoning, knowledge extraction and
decision processes. In Greco, S. and et al., edi-
tors, Proceedings of RSCTC 2006, volume 4259
of LNCS, pages 15–26. Springer.
Dubois, D. and Prade, H. (2008). An introduction to
bipolar representations of information and pref-
erence. International Journal of Intelligent Sys-
tems, 23(8):866–877.
Dubois, D. and Prade, H. (2009). An overview of
the asymmetric bipolar representation of positive
and negative information in possibility theory.
Fuzzy Sets and Systems, 160(10):1355–1366.
Facchinetti, G., Ghiselli Ricci, R., and Muzzioli,
S. (1998). Note on fuzzy triangular numbers.
13:613 – 622.
Gehrke, M. and Walker, E. (1992). On the structure
of rough sets. Bulletin of Polish Academy of Sci-
ences. Mathematics, 40:235–245.
Hickey, T., Ju, Q., and Van Emden, M. H. (2001). In-
terval arithmetic: From principles to implemen-
tation. Journal of the ACM, 48(5):1038–1068.
Ladenson, P. and Kim, M. (2011). Thyroid. In Gold-
man, L. and Schafer, A. I., editors, Goldman’s
Cecil Medicine, page Chap. 233, Philadelphia,
Pa. Saunders Elsevier.
Marek, V. W. and Truszczy
´
nski, M. (1999). Contribu-
tions to the theory of rough sets. Fundam. Inf.,
39(4):389–409.
Moore, R. E., Kearfott, R. B., and Cloud, M. J.
(2009). Introduction to Interval Analysis. So-
ciety for Industrial and Applied Mathematics
(SIAM), Philadelphia, PA, USA.
Pagliani, P. (1998). Rough set theory and logic-
algebraic structures. In Orłowska, E., editor, In-
complete Information: Rough Set Analysis, vol-
ume 13 of Studies in Fuzziness and Soft Comput-
ing, pages 109–190, Heidelberg. Physica-Verlag.
Pawlak, Z. (1981). Information systems theoreti-
cal foundations. Information Systems, 6(3):205–
218.
Pawlak, Z. (1982). Rough sets. International
Journal of Computer and Information Sciences,
11(5):341–356.
Pawlak, Z. (1991). Rough Sets: Theoretical Aspects
of Reasoning about Data. Kluwer Academic
Publishers, Dordrecht.
Pawlak, Z. and Skowron, A. (2007). Rudiments of
rough sets. Information Sciences, 177(1):3–27.
Sengupta, A. and Pal, T. K. (2000). On comparing
interval numbers. European Journal of Opera-
tional Research, 127(1):28–43.
Wang, Y.-M., Yang, J.-B., and Xu, D.-L. (2005). A
preference aggregation method through the esti-
mation of utility intervals. Comput. Oper. Res.,
32(8):2027–2049.
Wong, S. K. M., Wang, L., and Yao, Y. Y. (2013).
Interval structure: A framework for representing
uncertain information. CoRR, abs/1303.5437.
Xu, Z. and Chen, J. (2008). Some models for deriving
the priority weights from interval fuzzy prefer-
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
346

ence relations. European Journal of Operational
Research, 184(1):266–280.
Xu, Z. and L. Da, Q. (2002). The uncertain OWA
operator. 17:569–575.
Yager, R. R. and Alajlan, N. (2017). Approximate
reasoning with generalized orthopair fuzzy sets.
Information Fusion, 38(C):65–73.
Yao, Y. and Li, X. (1996). Comparison of rough-set
and interval-set models for uncertain reasoning.
Fundamenta Informaticae, 27(2,3):289–298.
Yao, Y. Y. (2009). Interval sets and interval-set alge-
bras. In 2009 8th IEEE International Conference
on Cognitive Informatics, pages 307–314.
Yao, Y. Y. and Wong, S. K. M. (1997). Interval
approaches for uncertain reasoning. In Pro-
ceedings of the 10th International Symposium
on Foundations of Intelligent Systems, ISMIS
’97, pages 381–390, London, UK, UK. Springer-
Verlag.
Measuring and Ranking Bipolarity via Orthopairs
347