Modelling Expressions of Physical Quantities
Blair D. Hall
a
Measurement Standards Laboratory of New Zealand, 69 Gracefield Road, Lower Hutt, New Zealand
Keywords:
Measurement Unit, Physical Quantity, Dimension, Quantity Calculus, Level of Measurement.
Abstract:
To express a quantity in conventional scientific notation, a number is paired with a unit of measurement,
like 10 m · s
−1
. However, this notation can be ambiguous and may require people to understand the context
in order to resolve interpretation difficulties. Also, the notation is intended to describe a certain type of
scientific data and is ill-equipped to express other kinds of measurement results. This paper discusses an
alternative formalism that is suitable for digital systems and overcomes many of the difficulties associated
with conventional written notation. We present the proposal using modelling elements that are closely related
to scientific concepts that underpin a wide range measurements. The alternative format for expressions is a
triplet: a number and a pair of references to information stored centrally. The mathematical properties of data
and, in a general sense, the property that is measured, can be captured in this extended format.
1 INTRODUCTION
Meaningful scientific communication needs a shared
understanding of the elements of language used to de-
scribe data, including the intended meanings of unit
and quantity names and symbols. The International
System of Units (SI) is generally preferred for scien-
tific work (BIPM, 2019), although some groups find
it convenient to adopt other units, or modify SI unit
notation to better suit their needs. Many customary
units are also used outside scientific communities.
The preferred scientific notation for physical data
does not always capture important information. So,
effective exchange of information about physical
quantities relies on skilled people who can access
contextual information and recognise appropriate in-
terpretations of data. Those skills are acquired dur-
ing years of formal education; but digital systems
would benefit from more direct logical representation
of data. This paper discusses some of the difficulties
with our current scientific notation and suggests a for-
malism better suited to digital systems.
To express a quantity in conventional notation, a
number is paired with a unit of measurement, like
10 m · s
−1
(BIPM, 2019). This notation is comple-
mentary to a form of scientific modelling in which
mathematical expressions describe relationships be-
tween quantities without any reference to units of
measurement (e.g., Newton’s second law, f = ma).
a
https://orcid.org/0000-0002-4249-6863
Terms in these so-called quantity equations represent
abstract physical quantities and the rules governing
permissible mathematical operations (known as the
quantity calculus) are formulated in terms of the kind
of quantity of each term. A quantity equation can be
evaluated when ‘concrete quantities’ (i.e., a number
and a unit) are provided for each term (Lodge, 1888).
Several important assumptions are made about the
semantics of terms in quantity equations. The quan-
tity concept encompasses the amount of a quantity
that is attributed a value of zero. This is often said
to be a natural zero (e.g., we may describe a length
as being zero without concern for units). It is further
assumed that a ratio of two terms for the same kind
of quantity does not depend on units (e.g., a linear
scale factor is a ratio of lengths that does not depend
on any unit of length). These two assumptions allow
the notion of a physical dimension to apply to terms
(Fourier, 1878), where a dimension may be thought
of as the class of units that can be used to express a
particular quantity (Ellis, 1964). This, in turn, allows
the analytical technique of dimensional analysis to be
applied to quantity equations (Barenblatt, 1987).
However, different types of measurement can at-
tribute the value of zero to different physical refer-
ences. For example, Fahrenheit temperature and Cel-
sius temperature adopt different reference tempera-
tures as zero, so each can be considered a quantity
in its own right, with a distinct dimension. There is,
however, no benefit in doing so. Quantity equations
216
Hall, B.
Modelling Expressions of Physical Quantities.
DOI: 10.5220/0012190300003598
In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 2: KEOD, pages 216-223
ISBN: 978-989-758-671-2; ISSN: 2184-3228
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

cannot express the relationships between these quan-
tities, or with thermodynamic temperature, nor can
the different dimensions associated with Fahrenheit,
Celsius, and thermodynamic temperatures be related
to each other.
Nevertheless, when physical data is incompatible
with quantity equations, it can still be used in what
are called numerical value equations. These equations
specify the form of expression for each term to ensure
that appropriate numbers are used in calculations. For
instance, a numerical value equation is given in the
SI Brochure that relates Celsius temperature to tem-
perature expressed in kelvin, t/
◦
C = T /K − 273.15
(BIPM, 2019). This equation uses t for a Celsius tem-
perature (with zero at the ice point, which is equiva-
lent to 273.15 K) and T for temperature expressed in
kelvin. The stylistic flourish of dividing terms by ap-
propriate units is a way of indicating the data required,
and harks back to the quantity concept. However, nu-
merical value equations may use any convenient no-
tation.
Scientific notation for physical quantities and the
idea of a formal quantity calculus supporting quan-
tity equations took shape in the 19th century; how-
ever, since then, a broader classification of measure-
ment scale types has been developed, which cov-
ers a range of different measurement methodologies
(Stevens, 1946). The issues associated with current
notation can be addressed by these ideas, which can
be usefully incorporated in digital representations of
physical data.
The remainder of this article is organised as fol-
lows. Section 2 reviews, in a series of subsections,
the scientific ideas involved in current notation and
explains some of the modelling difficulties. Then,
subsection 2.5 explains more about the classification
of types of measurement scales, which is needed in
the proposed formalism but is not part of conven-
tional notation. Section 3 describes a model that can
overcome current notational difficulties to represent a
broad range of measurement data. Section 4 discusses
further how modelling elements relate to basic mea-
surement concepts and section 5 summarises the main
points made in the paper.
2 THE CURRENT APPROACH
2.1 The SI
The modern SI is based on the idea of a formal
unit system proposed by Maxwell (Maxwell, 1873).
These unit systems are built up from a small set of
base quantities, with a corresponding set of quan-
tity dimensions, and a set of base units. Relation-
ships between quantities in the system are established
by quantity equations involving the base quantities.
These relationships can be associated with expres-
sions that take the form of products of powers of base
dimensions, which we call system dimensions (e.g.,
the SI system dimension for speed is LT
−1
, the dimen-
sion for length divided by the dimension for time).
1
Compound names for derived-quantity units are
generated systematically by replacing terms in a
system dimension with the corresponding base-unit
name. This produces names like, kg · m · s
−2
(cor-
responding to the system dimension MLT
−2
, where
M is the SI symbol for the mass dimension). These
names are effectively mnemonics for the system di-
mensions.
The SI has seven base quantities: mass, length,
time, electrical current, thermodynamic temperature,
amount of substance, and luminous intensity; and
seven corresponding units: kg, m, s, A, K, mol, and
cd, respectively (BIPM, 2019). However, the relation-
ships between some unit names and quantities is one-
to-many, because system dimensions can sometimes
be associated with several quantities. For instance,
the kg · m
2
· s
−2
is an acceptable unit for both torque
and energy (BIPM, 2019, section 2.3.4).
The SI also defines 22 special unit names and
symbols (e.g., rad,
◦
C, Ω, etc.). Like the base units,
these special units are associated with specific quan-
tities so, when the quantity is known, theses names
can be used interchangeably with the correspond-
ing compound names (e.g., the volt, V, may replace
kg · m
2
· s
−3
· A
−1
).
2.2 Challenges Posed by SI Notation
A formal unit system based on quantities and dimen-
sions is a simple, elegant, and logical idea. There
would be no particular difficulty in representing this
concept. However, the SI is a dynamic system that
continues to evolve. While adopting a pragmatic ap-
proach over the years, it has adopted features that cre-
ate modelling difficulties (Foster, 2009a; Mills, 2009;
Foster, 2009b). Four main difficulties are apparent.
Quantities Cannot be Uniquely Identified. Each
of the base SI units and the special units is
associated with a kind of quantity. However, the
1
The term ‘dimension’ is commonly used for a system
dimension; but this is misleading, because these expres-
sions do not designate actual dimensions—classes of sim-
ilar scales for a particular kind of quantity. As explained
by Emerson, “To say that two quantities are of the same di-
mension implies a relationship that has significance when
in fact it has none” (Emerson, 2005).
Modelling Expressions of Physical Quantities
217

same cannot be said for other SI unit names. In
general, the kind of quantity cannot be deter-
mined from the unit symbol alone. For example,
the SI has a special unit joule (J) for energy but
the compound units N · m and kg · m
2
· s
−2
are
legitimate alternatives for expressing both torque
and energy (BIPM, 2019, section 2.3.4).
Unit Conversion is Sometimes Quantity-Dependent.
The special unit names can complicate rules for
permissible unit conversions. For example, the
special name for the unit of activity, the becquerel
(Bq), may always be replaced by the reciprocal
second (s
−1
), whereas data expressed in s
−1
may
not be expressed in Bq unless the expression is
known to be a measure of activity, because s
−1
is
also a unit for angular frequency.
Quantities Representing Temperature are Unusual.
Relationships between expressions in kelvin and
degrees Celsius are unusually complicated. The
kelvin is the SI base unit for thermodynamic
temperature and the degree Celsius is a special
unit name for temperature. The numerical value
of a temperature difference is the same when
expressed in either unit. However, Celsius
temperature places zero at the ice point, while
zero on the kelvin scale refers to absolute zero of
thermodynamic temperature. Transformation of
temperatures between kelvin and degrees Celsius
must take the different zeros into account (Hall
et al., 2023).
Dimensionless Quantities are not Plain Numbers.
The class of dimensionless quantities contains a
large number of quantities that can be expressed
in the SI unit one. Only two special names
for dimensionless quantities are defined (the
radian, for plane angle, and the steradian, for
solid angle), so most dimensionless quantities are
expressed in terms of the unit one, which provides
no information about the kind of quantity. In
practice, dimensionless-quantity data is often
treated as plain numbers, but these quantities
have unique characteristics that are not generally
comparable to each other. Notation showing a
ratio of unit symbols is encouraged (e.g., mm/m,
g/kg, etc.), as this can convey useful information.
However, not all dimensionless quantities are
simple ratios of the same kind of quantity (e.g.,
the dimensionless numbers that arise in fluid
mechanics (Wikipedia, 2023)).
These types of problem are known. Some are
brought to the attention of readers in the SI Brochure,
so people can act to mitigate their impact.
2.3 Units Outside the SI
The SI has strict formatting rules and style conven-
tions, which are intended to ensure that notation is
used consistently. However, there are groups that de-
viate from the rules, and sometimes alternative sym-
bols, or even alternative interpretations of standard
symbols, are adopted, effectively introducing ad hoc
notation.
For example, some specialists in humidity and hy-
grometry favour the symbol %rh to express the di-
mensionless quantity relative humidity. This breaks
SI rules by annotating the percent symbol (%, repre-
senting 1/100) with ‘rh’ to indicate a kind of quantity.
Another example is when symbols are introduced to
identify particular chemical elements. For instance,
12 kg C may be intended to express a mass of the
chemical element carbon; but the symbol C represents
a coulomb—the special SI unit for electric charge.
Customary units are often organised into systems,
like the British Imperial System of units (Encyclopae-
dia Britannica, 2019). However, these systems do not
have a formal structure: no base quantities or units are
defined. Most customary units are not accepted for
use in the SI. However, authoritative conversion fac-
tors to SI equivalents are sometimes published (e.g.,
(Butcher et al., 2006)). When authoritative conver-
sion factors are available, data can be disseminated
in customary units while maintaining a strict relation-
ship to SI units.
2.4 Kind of Quantity
The earliest description of quantity calculus is at-
tributed to Lodge (Lodge, 1888; Copley, 1960). He
explained that terms in a quantity equation are associ-
ated with ‘kinds of quantity’, and that, if equality is to
be meaningful, both sides of an equation must repre-
sent quantities of the same kind. This requirement is
reminiscent of dimensional homogeneity, but Lodge
reminded readers that homogeneity is not a sufficient
condition for quantities to be of the same kind, and
gave examples where an understanding of the physics
is needed to identify the kinds of quantity.
Although Lodge referred to kinds of quantity for
terms when describing quantity calculus, he made no
attempt to define this terminology. We assume the
ordinary English sense of ‘kind’ is adequate: as be-
ing of the same class, sort, or variety. So, length is
both the name of a quantity and of a kind of quantity,
whereas breadth, height, thickness, radius, diameter,
circumference, etc., are all names of quantities, but
they are not quantity kinds. The ISO 80000 standard,
which documents the International System of Quan-
KEOD 2023 - 15th International Conference on Knowledge Engineering and Ontology Development
218

tities, also interprets ‘kind of quantity’ in this sense
(ISO, 2013).
Kinds of quantity are used to establish acceptable
computational steps. There is no restriction on multi-
plication of terms, but only terms associated with the
same kind of quantity may be added or subtracted. Di-
vision is interpreted as the inverse of multiplication,
and terms may be exponentiated as an alternative no-
tation for multiplication and division. Dimensionless
quantity terms are considered pure numbers in the cal-
culus, allowing non-linear operations (e.g., trigono-
metric, logarithmic, and exponential functions) to be
applied, and the results to be treated as pure numbers
as well.
The kind of quantity of a sum or difference is the
same as the terms involved, which seems self-evident:
the clich
´
e that apples cannot be added to oranges is
even more compelling when quantities such as length
and time are considered. However, the calculus has no
way of determining the kind of quantity for a product
or quotient. A product is simply understood as being
proportional to its factors, while a quotient is propor-
tional to factors in the numerator and inversely pro-
portional to factors in the denominator (Lodge, 1888).
2.5 Types of Scale
During the first half of the 20th century, research dis-
ciplines outside the traditional physical sciences were
challenged about the validity of quantitative data ob-
tained without the underlying conceptual support of
notions like a physical quantity. From this debate, a
classification scheme for different types of measure-
ment emerged (Stevens, 1946). This classification re-
lates certain types of experimental procedures to the
mathematical properties of data obtained.
Four fundamental types of measurement scale
were identified: ratio, interval, ordinal, and nominal.
All of these are important to metrology (White, 2010),
although we focus on ratio and interval scales here.
Each scale type can be associated with a mathe-
matical transformation that preserves certain proper-
ties of the data and does not change the type of scale.
For a ratio scale, multiplication by any positive num-
ber transforms data to another ratio scale. This corre-
sponds to the familiar process of unit conversion for
quantities, which does not affect data ratios (e.g., as-
pect ratio or linear scale factor).
Affine functions transform one interval scale to
another by applying a scale factor and an offset. The
Fahrenheit and Celsius temperature scales are exam-
ples of interval scales. Conversion from one to the
other requires an adjustment for the different refer-
ence points associated with zero and a rescaling of the
Figure 1: An expression is a triplet, consisting of a number
with references to a scale and an aspect. To accommodate
legacy data, the aspect reference is shown as optional; but if
no aspect is specified, fewer legitimate forms of expression
can be identified. This figure, and those following, are class
diagrams in the unified modelling language (UML) version
2.5 (Object Management Group, 2015).
data (the degree Fahrenheit is smaller than the degree
Celsius). The arithmetic mean and standard deviation
are not affected by affine transforms. For example, the
following two processes yield the same result: 1) take
the mean of a sample of data in degrees Fahrenheit
and transform it to degrees Celsius; or 2) transform
data in degrees Fahrenheit to degrees Celsius and take
the mean.
3 MODELLING QUANTITY
EXPRESSIONS
This section describes a more detailed formalism for
expressions of physical data that avoids the diffi-
culties with unit notation identified above (Hall and
Kuster, 2022; Hall, 2023). This can be thought of as
extending the conventional formalism.
A datum is expressed as a triplet (figures 1 and
2): a number accompanied by references to an aspect
and a scale. This corresponds to an English phrase
like “9.8 is the acceleration expressed in kg · m · s
−2
on a ratio scale” (acceleration is the aspect and the SI
unit combined with the ratio scale-type is the scale).
An aspect may be regarded as a generalisation of
the role played by a kind of quantity. This is explained
further in subsection 3.2. A scale may be regarded as
a generalisation of the role played by a unit. Scales
are defined by associating a unit, and perhaps other
appropriate references, with a scale type. For exam-
ple, a scale can be defined for temperature by asso-
ciating the unit degree Celsius, a reference to the ice
point (at 0
◦
C), and the interval scale type.
In digital records, expressions hold a numeric
value and unique identifiers for the aspect and scale
(figure 2). The identifiers refer to digital objects that
encapsulate information about what is expressed and
how. These objects are stored in a central registry,
which can be indexed by the identifiers. The purpose
of using identifiers for the aspect and scale is to ensure
Modelling Expressions of Physical Quantities
219

that alternative legitimate expressions for data can be
identified. This is achieved using a table of expres-
sion transformations in the central registry, indexed
by aspect–scale identifier pairs.
<root xmlns:mlayer="http://mlayer.org/ns">
<mlayer:Expr>
<mlayer:Number x=12.3>
<mlayer:Aspect id="AS2"/>
<mlayer:Scale id="SC1"/>
</mlayer:expr>
</root>
Figure 2: Digital records identify an aspect and a scale in
expressions, as shown in this XML snippet. The succinct
identifiers index more detailed information in a central reg-
ister. Figures 5 and 6 show more details for the scale (kg)
and the aspect (mass), respectively.
3.1 Scale
The different types of scale may be regarded as
specialisations of a generic type (figures 3 and 4),
which captures the attributes needed. For example,
a Unit is associated with both a RatioScale and an
IntervalScale, but an IntervalScale is also asso-
ciated with a Reference that defines one point on the
scale (figure 4).
In systems like the SI (here qualified as formal
unit systems), each unit is associated with a product
of powers of base dimensions (here called a system
dimension). For instance, the system dimension LT
−2
is associated with the unit for acceleration, m · s
−2
.
However, customary unit systems do not define base
quantities or base units. So, units in these systems
may be associated with ratio scales but the notion of
system dimensions does not apply.
The UML class diagram in figure 3 shows rela-
tionships between system, ratio scale, unit and sys-
tem dimension. Figure 5 shows an example of a scale
object representing the ratio scale for the SI kilogram.
As explained in section 2.2, when Celsius temper-
ature is considered a quantity, its relationship to ther-
modynamic temperature is lost (only numerical value
equations relate expressions of temperature in differ-
ent units). However, most specialists in temperature
measurement would not think of Celsius temperature
as being a different quantity to thermodynamic tem-
perature. A better representation of scientific under-
standing is provided by explicit scales, such as the
degree Celsius paired with the interval scale type, and
the kelvin paired with the ratio scale type. These
scales can be associated with an aspect for temper-
ature. This use of aspect is more general than the
quantity concept applied to Celsius temperature and
thermodynamic temperature (which attribute different
temperatures to zero).
3.2 Aspect
In the conventional expression of a quantity, the kind
of quantity may be hard to determine unless it can be
inferred directly from a special unit name, or a base
unit name. The formalism proposed here overcomes
this difficulty by making explicit reference to an as-
pect, which may be used to disambiguate data. For
example, knowing that a datum expressed in s
−1
on
a ratio scale is associated with the aspect frequency
establishes equivalence with an alternative expression
in Hz. Aspects can address difficulties in the inter-
pretation of SI units related to the concept of quantity
(and hence kind of quantity), but they can also be used
to denote measurable properties in a wider sense than
kinds of quantity.
One difficulty arises because temperature differ-
ences are expressed in degrees Celsius on a ratio
scale, but absolute temperatures are expressed in de-
grees Celsius on an interval scale. So, in degrees Cel-
sius, the scale type can disambiguate between tem-
perature data and temperature differences. However,
both forms of expression can be converted to kelvin
on a ratio scale, after which the quantity is ambigu-
ous. Explicit reference to the kind of quantity cannot
resolve this problem. As explained in section 2.4, the
kind of quantity is always the most general sense of
a quantity—the superordinate class. So, the kind of
quantity of a temperature difference is the same as a
temperature (this is reflected in the dimensional ho-
mogeneity requirement for a quantity equation like
∆T = T −T
0
, for the difference between temperatures
T and T
0
). Instead, distinct aspects for absolute tem-
perature and temperature difference can be used to re-
solve this ambiguity (see figure 7).
Aspects are also useful for dimensionless quan-
tities, many of which represent ratios of the same
kind of quantity, such as aspect ratio and linear scale
factor (both length ratios). Although all dimen-
sionless quantities have identical system dimensions,
many are arguably distinct kinds of quantity (Ellis,
1964). Some dimensionless quantities are best rep-
resented as particular quantity kinds—angle being a
good example—while others may be best represented
as quantity ratios, in which case the aspect is the ratio
of the quantity kinds for the numerator and denomina-
tor. For instance, data for both a linear scale factor and
an aspect ratio will be associated with a length-ratio
aspect (similar to notation that shows unit ratios, like
mm/m), although the nature of the lengths is different
(lengths are perpendicular in an aspect ratio, but they
are collinear in a linear scale factor).
KEOD 2023 - 15th International Conference on Knowledge Engineering and Ontology Development
220

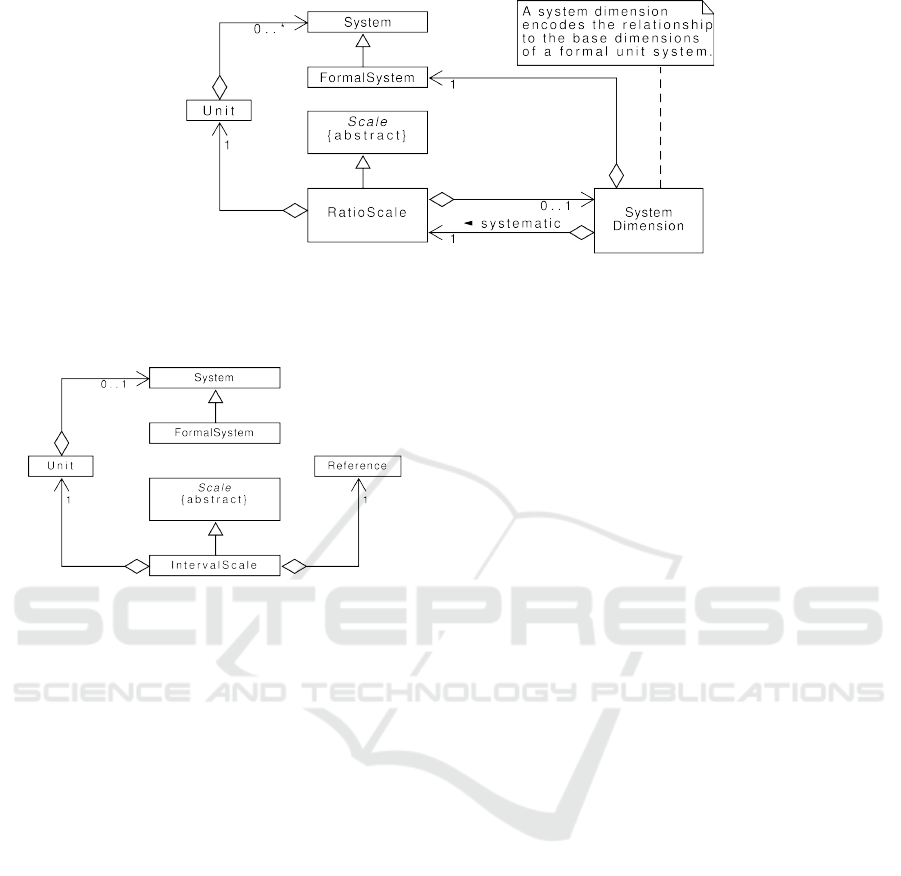
Figure 3: A RatioScale is associated with a unit, and may be associated with a system dimension (a product of powers of the
base dimensions in a formal unit system—often encoded as a sequence of integers). Many ratio scales can be associated with
a single system dimension, but just one has the unit with a name derived from the system dimension. This scale is designated
‘systematic’. No system dimension is associated with scales for units that do not belong to a formal system.
Figure 4: An IntervalScale is associated with a unit,
which may be part of a unit system. In addition to the
unit (which determines the size of scale divisions), the
Reference establishes a physical reference to one point on
the scale (often defining the zero point).
{
"id": "SC1",
"ml_name": "ra_si_kg",
"type": "ratio",
"unit_id": "UN1",
"system_dimension_id": "DI1",
}
Figure 5: A JSON object representing a RatioScale asso-
ciated with the SI kilogram (some details are elided). Unit
and system dimension identifiers index further information.
The aspect may be used to distinguish between
measurements of closely related but different proper-
ties. Physical properties of practical importance are
sometimes difficult to measure when a large number
{
"id": "AS2",
"ml_name": "as_mass",
"name": "mass",
}
Figure 6: A JSON object representing the Aspect mass
(some details are elided). References to external informa-
tion about the physical concept mass would be provided but
are not shown.
of factors can influence measurement results. In such
cases, standard methods may be developed. These al-
low measurements to be made in a reproducible man-
ner, so results can be compared with similar data ob-
tained according to the same standard. One example
is viscosity, for which there may be as many as a hun-
dred different standard methods, each defining a pro-
tocol suited to specific needs for information (White,
2010). Viscosity may be expressed in SI units but, if
data is to be compared in any meaningful sense, the
method of measurement has to be identifiable. Aspect
can be used for this purpose.
4 DISCUSSION
The purpose of the formalism described here is to cap-
ture information about data in sufficient detail to en-
able other legitimate forms of expression to be iden-
tified. In other words, it supports the abstract notion
of a measurable magnitude that can be expressed in
different but equivalent ways. Our modelling ele-
ments represent the various constructs and measure-
ment concepts involved in the expression of data. The
relationships between these elements do not seem to
have been modelled before.
Many attempts to find satisfactory digital repre-
sentations for units of measurement for programming
languages and databases have been made over the
years—see (McKeever et al., 2021) for a recent re-
view. There are also a number of ontologies that de-
fine quantities and units—see (Aameri et al., 2020).
Nevertheless, there is often confusion about funda-
mental concepts, like quantity, dimension, and quan-
tity calculus. For example, a digital encoding resem-
bling system dimensions is often used to represent
quantity kinds and units. This can produce appar-
ently nifty software; however, it does not accurately
Modelling Expressions of Physical Quantities
221

⟨T ⟩J
◦
C,IK
⟨∆T ⟩J
◦
C,RK
⟨T
90
⟩J
◦
C,IK
⟨∆T
90
⟩J
◦
C,RK









◦
C
⟨T ⟩JK, RK
⟨∆T ⟩JK, RK
⟨T
90
⟩JK,RK
⟨∆T
90
⟩JK,RK









K
⟨T ⟩J°F, IK
⟨∆T ⟩J°F, RK

°F
⟨T
90
⟩J°F,IK
⟨∆T
90
⟩J°F,RK

°F
Figure 7: Pairing of an aspect and a scale allows different
types of temperature data to be expressed without ambigu-
ity. Aspect–scale pairs are shown grouped with the cor-
responding conventional unit symbol. Angle brackets ⟨·⟩
indicate an aspect and J·K a scale. ⟨T ⟩ is thermodynamic
temperature, or temperature difference when prefixed by ∆.
⟨T
90
⟩ is a defined scale that approximates thermodynamic
temperature (Hall et al., 2023). The scale types are: R, for
ratio scale; and I, for interval scale.
represent the underlying metrological concepts and,
although extra dimensions can be added for internal
use, it is vulnerable to the type of problems with am-
biguity discussed above for SI system dimensions.
Figure 7 illustrates the proposed approach applied
to temperature data. As mentioned in §2.2, the kelvin
(K) and degree Celsius (
◦
C) are both SI units for tem-
perature, but the relationships between data expressed
in these units can be complicated. Also shown is the
degree Fahrenheit (°F), which is a commonly used
customary unit in the United States. In addition, there
is a widely used method-defined temperature scale
called ITS-90 that approximates thermodynamic tem-
perature. The figure shows that different types of
data can be resolved by using explicit aspects and
scales. This makes it possible to identify alternative
expressions. For instance, the conversion of temper-
ature data from
◦
C to °F has multiple interpretations
(such as the illegitimate conversion from ⟨T ⟩J
◦
C,IK
to ⟨∆T ⟩J°F,RK), whereas an explicit conversion from
⟨T ⟩J
◦
C,IK to ⟨T ⟩J°F, IK) is unambiguous (and legiti-
mate).
Using aspect–scale identifier pairs, a table of
transformations that map between expressions can be
maintained in a central register. Entries in this reg-
ister are indexed by aspect–scale pairs for the initial
and final expressions. The table holds numerical coef-
ficients and mathematical functions to transform from
one expression to another. This register-based ap-
proach accurately captures the nature of relationships
between expressions without being limited to partic-
ular unit systems. The register can include mappings
based on data published by authoritative bodies when
the units involved do not belong to the same system.
Certain sets of mappings in this table are useful
and interesting. For example, the general notion of
dimension—a class of similar ratio scales for a quan-
tity (Ellis, 1964)—corresponds to the set of mappings
between the ratio scales paired with a given aspect.
For example, units of length, like the inch, yard, etc.
are not recognised by the SI. However, authoritative
conversion factors from these units to the metre are
published (Butcher et al., 2006), so ratio scales for
these units will be included in the dimension set for
length by virtue of the known transformations.
Another example is the dimension set for angle,
which has mappings between ratio scales associated
with an angle aspect. The radian is a special name
for the unit of plane angle and the imperial unit for
plane angle—the degree—is an accepted non-SI unit.
Scales associated with these units are included in the
dimension set for angle because there are recognised
transformations.
There are other useful sets of related expressions
that can be identified in the table. There is the set of
mappings between all interval scales for a given as-
pect, which is analogous to the dimension set. For ex-
ample, the interval-scale expressions for temperature
in degrees Celsius and degrees Fahrenheit are related
by affine transformations, which would be included in
such a set. Similarly, and perhaps more useful, there
are the sets of mappings between different types of
scale for a given aspect. For instance, temperature ex-
pressed in kelvin on a ratio scale may be transformed
to temperature in degrees Celsius on an interval scale.
The ideas presented here are being implemented
as an online service with a RESTful interface to
a cloud-based register. This project, in collabora-
tion with the Measurement Information Infrastructure
technical committee 141 (MII) of the NCSL Intera-
tional organisation.
2
), is at an early stage, so details
may change. Governance of data in the register will
be provided by the MII committee under the auspices
of NCSL International.
5 CONCLUSIONS
A formalism that overcomes many of the difficul-
ties associated with conventional notation for physi-
cal quantity data has been discussed. The scientific
concepts that underpin expressions of quantities can
be clearly related to elements of the formalism used
to model data. Conventional notation for written ex-
pression of quantities is intended for skilled people
and sometimes requires supplementary contextual in-
formation to be interpreted. This lack of expressive-
2
Founded under the name ‘National Conference of
Standards Laboratories’, this global non-profit organisation
is now known as NCSL International (see, https://ncsli.org/
page/AB
KEOD 2023 - 15th International Conference on Knowledge Engineering and Ontology Development
222

ness is addressed in the alternative formalism by in-
cluding information about the mathematical structure
of data (the scale type) and the nature, in a general
sense, of the property that was measured (the aspect).
The conventional couple notation, of a number with a
unit symbol, is replaced by a triplet: a number and a
pair of digital identifiers that refer to centrally-stored
information concerning the measured aspect and the
scale of measurement. A central register of transfor-
mations that map between alternative forms of expres-
sion allows sets of related aspect–scale expressions to
be identified. One such category of sets corresponds
to the general notion of a quantity dimension.
ACKNOWLEDGEMENTS
This work was funded by the New Zealand govern-
ment. The author is grateful to Mark Kuster, Ryan
White, Flavio Rizzolo, and Peter Saunders for help-
ful discussions, and to Peter Saunders for carefully
reviewing this work.
REFERENCES
Aameri, B., Chui, C., Gr
¨
uninger, M., Hahmann, T., and Ru,
Y. (2020). The FOUnt ontologies for quantities, units,
and the physical world. Applied Ontology, 15(3):313–
359.
Barenblatt, G. I. (1987). Dimensional analysis. Gordon and
Breech.
BIPM (2019). The International System of Units. BIPM,
S
`
evres, France, 9
th
edition.
Butcher, K. S., Crown, L. D., and Gentry, E. J. (2006). The
international system of units (SI)—conversion factors
for general use. US Department of Commerce, Na-
tional Institute of Standards and Technology.
Copley, G. N. (1960). William stroud and quantity calculus.
Nature, 188:254.
Ellis, B. (1964). On the nature of dimensions. Philosophy
of Science, 31(4):357–380.
Emerson, W. H. (2005). On the concept of dimension.
Metrologia, 42(4):L21–L22.
Encyclopaedia Britannica (2019). Imperial units. https://
www.britannica.com/topic/Imperial-unit (accessed 20
June 2023).
Foster, M. P. (2009a). Disambiguating the SI notation
would guarantee its correct parsing. Proceedings of
the Royal Society A: Mathematical, Physical and En-
gineering Sciences, 465(2104):1227–1229.
Foster, M. P. (2009b). Response to Mills’ comments on
the SI notation. Proceedings of the Royal Society
A: Mathematical, Physical and Engineering Sciences,
465(2108):2317–2318.
Fourier, J. B. J. (1878). The analytical theory of heat. Cam-
bridge University Press.
Hall, B. (2023). Representing and expressing measure-
ment data in digital systems. SN Computer Science,
4(2):120.
Hall, B. and Kuster, M. (2022). Representing quantities
and units in digital systems. Measurement: Sensors,
23:100387.
Hall, B., Saunders, P., and White, D. R. (2023). Dig-
ital representation of scales and units for temper-
ature and related quantities. Temperature: Its
Measurement and Control in Science and Industry
(Proc. 10
th
Int. Temp. Symp.). accepted.
ISO (2013). Quantities and units – Part 1: General (BS EN
ISO 80000-1:2013). British Standards Institution.
Lodge, A. (1888). The multiplication and division of con-
crete quantities. Nature, 38:281–283.
Maxwell, J. C. (1873). A Treatise on Electricity and Mag-
netism. Clarendon Press, Oxford.
McKeever, S., Bennich-Bj
¨
orkman, O., and Salah, O.-A.
(2021). Unit of measurement libraries, their popular-
ity and suitability. Software: Practice and Experience,
51(4):711–734.
Mills, I. (2009). Conventions for writing the values of
quantities in the SI. Proceedings of the Royal Society
A: Mathematical, Physical and Engineering Sciences,
465(2108):2313–2316.
Object Management Group (2015). Unified modeling lan-
guage specification (version 2.5). https://www.omg.
org/spec/UML/2.5 (accessed 28 August 2023).
Stevens, S. S. (1946). On the theory of scales. Science,
103(2684):677 – 680.
White, R. (2010). The meaning of measurement in metrol-
ogy. Accreditation and Quality Assurance, 16(1):31–
41.
Wikipedia (2023). Dimensionless numbers in fluid mechan-
ics. https://en.wikipedia.org/wiki/Dimensionless
numbers in fluid mechanics (accessed 22 June 2023).
Modelling Expressions of Physical Quantities
223