Towards Understanding Crossover for Cartesian Genetic Programming

Henning Cui

1 a

, Andreas Margraf

2 b

, Michael Heider

1 c

and J

org H

ahner

1 d

Institute for Computer Science, University of Augsburg, Am Technologiezentrum 8, 86159 Augsburg, Germany

Fraunhofer IGCV, Am Technologiezentrum 2, 86159 Augsburg, Germany

Keywords:

Cartesian Genetic Programming, CGP, Crossover, Reorder, Evolutionary Algorithm.

Abstract:

Unlike in traditional Genetic Programming, Cartesian Genetic Programming (CGP) does not commonly fea-

ture a recombination/crossover operator, although recombination plays an important role in other evolutionary

techniques, including Genetic Programming from which CGP originates. Instead, CGP mainly depends on

mutation and selection operators in their evolutionary search. To this day, it is still unclear as to why CGP’s

performance does not generally improve with the addition of crossover. In this work, we argue that CGP’s

positional bias might be a reason for this phenomenon. This bias describes a skewed distribution of active and

inactive nodes, which might lead to destructive behaviour of standard recombination operators. We provide

a ﬁrst assessment with preliminary results. No ﬁnal conclusion to this hypothesis can be drawn yet, as more

thorough evaluations must be done ﬁrst. However, our ﬁrst results show promising trends and may lay the

foundationf or future work.

1 INTRODUCTION

Cartesian Genetic Programming (CGP) is a form

of Genetic Programming (GP), based on directed

acyclic graphs whose nodes are arranged in a two-

dimensional grid (cf. Section 2 for a detailed descrip-

tion).

Since its inception in 1999 by Miller (Miller,

1999), the crossover operator is an active research

topic, as no universal recombination operator has

been found yet—as contrasted with GP, for which

numerous different crossover algorithms exist (Lang-

don et al., 2008). As for CGP, an effective crossover

operator relies on extensions to the CGP formula

and highly depends on the speciﬁc use case (Husa

and Kalkreuth, 2018). Moreover, it is still unclear

as to why crossover raises issues in the context of

CGP (Miller, 1999; Clegg et al., 2007; Miller, 2020;

Kalkreuth, 2020).

Regarding possible explanations for CGP’s issues

with crossover, we hypothesize that the positional

bias might be inﬂuential. In CGP, the positional bias

is an effect which potentially limits CGP to fully ex-

plore its search space (Goldman and Punch, 2013a).

https://orcid.org/0000-0001-5483-5079

https://orcid.org/0000-0002-2144-0262

https://orcid.org/0000-0003-3140-1993

https://orcid.org/0000-0003-0107-264X

The basic problem is a non-uniform distribution of

nodes contributing to an output. This, in turn, might

lead to problems for standard recombination opera-

tors like the point-, multi-n-, or uniform-crossover. To

counteract positional bias, Goldman and Punch intro-

duced Reorder, an operator to shufﬂe CGPs genome

ordering without changing its phenotype (Goldman

and Punch, 2013a). Thereby, the effect of the posi-

tional bias is supposedly lessened. To test our hypoth-

esis, we take advantage of Reorder. If the positional

bias plays a role in CGP’s issues with crossover, this

extensions might beneﬁt from the usage of crossover

and provide a better understanding of this issue.

We provide a quick overview of the core princi-

ples of CGP and reintroduce the Reorder operator,

as well as the positional bias in the following Sec-

tion 2. Afterwards, Section 3 gives an overview of

related work. In Section 4, we discuss our hypothesis

in-depth and discuss preliminary results in Section 5.

At last, Section 6 summarizes our ﬁndings and dis-

cusses future research directions.

2 CARTESIAN GENETIC

PROGRAMMING

The core principles of the supervised learning algo-

rithm called Cartesian Genetic Programming (CGP)

308

Cui, H., Margraf, A., Heider, M. and Hähner, J.

Towards Understanding Crossover for Cartesian Genetic Programming.

DOI: 10.5220/0012231400003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 308-314

ISBN: 978-989-758-674-3; ISSN: 2184-3236

are reintroduced in the following section—with the

ﬁrst description given by Miller (Miller, 1999). In ad-

dition, we present Reorder, which is introduced by

Goldman and Punch (Goldman and Punch, 2013a)

and extends the classic CGP formula.

2.1 Representation

Originally, CGP is represented as a directed, acyclic

and feed-forward graph. The graph contains nodes ar-

ranged in a c × r grid, with c ∈ N

and r ∈ N

deﬁn-

ing the number of columns and rows in the grid re-

spectively

The set of nodes can be divided into three groups:

input-, computational- and output-nodes. Input nodes

directly receive a program’s inputs. Computational

nodes are represented by a function gene and a con-

nection genes, with a ∈ N

being the maximum ar-

ity of all functions in the predeﬁned function set. At

last, output nodes redirect the calculated output of a

previous input- or computational node and deﬁne the

models output. They are represented by a single con-

nection gene.

Additionally, computational nodes can be clas-

siﬁed into active and inactive nodes. The former

nodes are part of a path to an output node and—as

a consequence—contribute to a program output. On

the contrary, inactive nodes do not contain a path to

an output node and, thereby, do not contribute to the

models output. This is also why their operations are

not computed for the evaluation of a ﬁtness value and

during inference time. However, inactive nodes are

essential to CGP as they probably aid the evolution-

ary process through genetic drift (Turner and Miller,

2015).

As is standard in most CGP variants, an elitist

(µ + λ)–evolution strategy with µ = 1 and λ = 4 is

used to select the best graph. This is combined with

neutral search to improve performance and conver-

gence time (Turner and Miller, 2015; Yu and Miller,

2001; Vassilev and Miller, 2000).

Regarding its mutation operator, a point mutation

is oftentimes found in literature (Miller, 2011; Miller,

2020). The caveat of the point mutation, however,

is its possibility that that only inactive genes are mu-

tated. Hence, it is not possible to evaluate the quality

of the mutation, as the phenotype did not change. This

could potentially lead to ﬁtness plateaus and longer

training times. In order to prevent such plateaus,

Goldman and Punch propose an alternative mutation

operator called Single (Goldman and Punch, 2013b).

Please note that, with today’s standards, a CGP model

typically consists of only one row (Miller, 2011). That

means, r = 1.

INPUT

ADD

SUB

ADD

OUTPUT

Figure 1: Example graph deﬁned by a CGP genotype. The

dashed node and connections are inactive due to not con-

tributing to the output.

With Single, the point mutation is applied to randomly

selected genes until a gene corresponding to an active

node is mutated. This forces changes in the phenotype

with no wasted evaluations being performed. Thus,

when the optimal mutation rate is not known, the au-

thors Goldman and Punch claim that Single should be

preferred (Goldman and Punch, 2013b).

An illustrative example of a graph deﬁned by a

CGP genotype can be seen in Figure 1. It shows a

graph with c = 6 and r = 1, which is supposed to solve

a task consisting of two inputs and one output. Here,

the ﬁrst two nodes (n

and n

) are input nodes and

provide two different program inputs. The follow-

ing nodes (n

–n

) are computational nodes. At last,

the output is provided by one output node n

. In this

example, both inputs are subtracted, with this inter-

mediate result being added to itself and taken as the

program output. Thus, every node drawn with a solid

line is an active node. The node n

is an inactive node

(marked by dashed lines) since it does not contribute

to the program output nor contains a path to an output

node.

2.2 Positional Bias and Reorder

CGP has many advantages, such as the absence of

bloat (Miller, 1999) and its small solutions (Miller,

2011). Nonetheless, it is far from perfect, with one of

its shortcomings being the positional bias.

2.2.1 Positional Bias

Goldman and Punch found a negative impact in

CGP’s search space by enforcing a feed forward

grid (Goldman and Punch, 2013a). Namely, a posi-

tional bias: A non-uniformity of the probability that

a node is active. Computation nodes near input nodes

have a higher probability of becoming active, while

nodes closer to the output nodes have the lowest prob-

ability of becoming active. In turn, the nodes near the

output nodes have a higher probability of becoming

inactive.

During the mutation of a connection gene, each

previous node has the same probability of being cho-

sen as the new starting node for the connection. How-

ever, nodes near input nodes have more options for

successor nodes, as directed edges are only allowed

Towards Understanding Crossover for Cartesian Genetic Programming

309

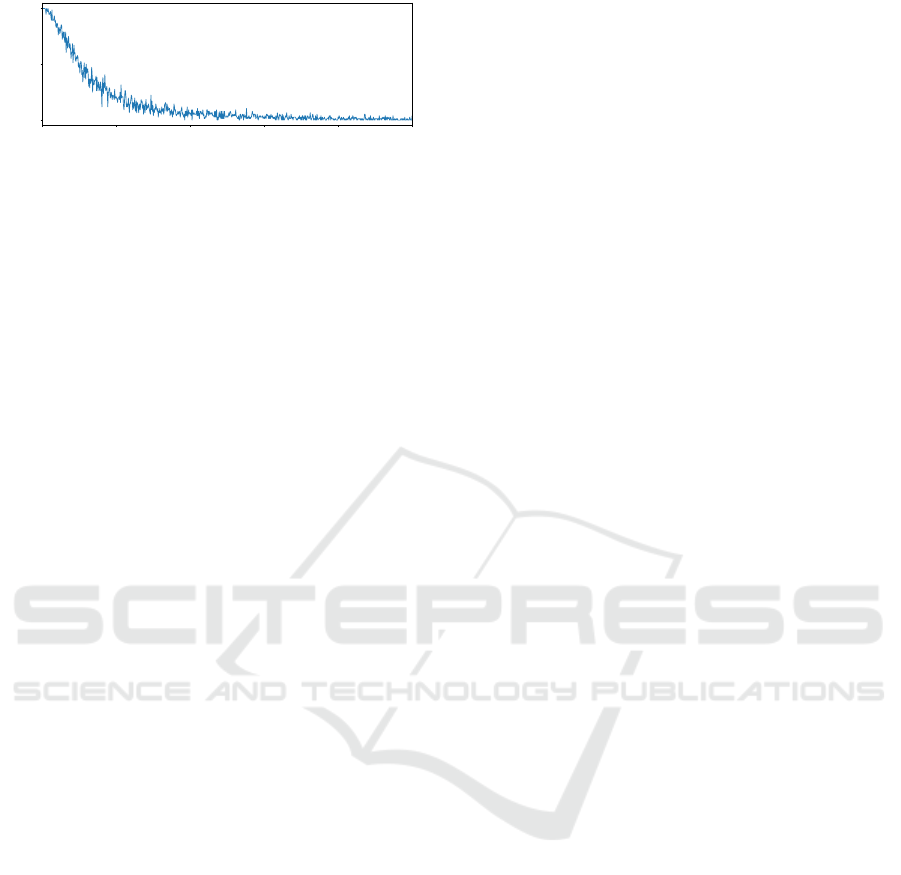
0 20 40 60 80 100

Relative node index in % to the graph's total length

0.0

0.5

1.0

% active

Figure 2: Example distribution of active nodes in CGP

graph solutions. The x-axis represents a node’s position in

the graph, the y-axis its percentage of being active, gener-

ated from 50 independent runs on the same dataset.

from left to right. This is why they have a higher

chance of becoming active, as a node is only active

when it is part of a path to an output node. Nodes

closer to output nodes have less options of being cho-

sen by other nodes, as they have less nodes in front.

With the help of Figure 1, the positional bias can

be exempliﬁed. In this example, n

’s possible suc-

cessors are n

–n

whereas n

’s possible successor is

just n

. Hence, four nodes can potentially mutate their

connection to n

and if one of those nodes is active, n

becomes active, too. Contrary, n

has only one node

in front: n

. This is also the only node which could

mutate its connection to n

An illustrative example of the active node distribu-

tion can be seen in Figure 2. We show the distribution

of active nodes, obtained from 50 independent runs

on the same dataset. Additionally, by modeling the

distribution of active nodes, the positional bias could

be quantitatively measured and described.

2.2.2 Reorder

The positional bias makes it difﬁcult or impossible to

solve certain problems (Goldman and Punch, 2013a;

Payne and Stepney, 2009). To weaken the effects of

this bias, Goldman and Punch proposed two new op-

erators which are executed before mutation: DAG and

Reorder (Goldman and Punch, 2013a).

The ﬁrst extension, DAG, allows each node to mu-

tate connections to every other node in the genome as

long as the new connection does not create a cycle.

However, as we do not build upon it, we will not dis-

cuss DAG in further detail.

Reorder shufﬂes the ordering of the genotype but

respects the sequence of operation of active nodes.

Hence, the phenotype does not change but, as a re-

sult, active nodes are dispersed through the grid.

This Reorder operator begins by creating a de-

pendency set D. It contains each computational node

and its information from which node it gets its input

from. Additionally, a new genome is initialized con-

taining all input and output nodes from the original

genome, as they do not get assigned a new position.

Afterwards, the set of addable nodes Q is created.

Initially, this set contains only computational nodes

whose dependencies are satisﬁed. In this context, sat-

isﬁed means the following: Let b be a computational

node, and a be a computational or input node from

which b gets one of its input from, with (b, a) ∈ D.

This means, there is a directed edge connecting a to

b via b’s connection gene. Then, b is satisﬁed when

all nodes from which b gets its input from are mapped

into the new genome.

With both sets initialized, the shufﬂing of the

genome is done by repeating the following steps:

1. Select and remove a random node a ∈ Q.

2. Map a sequentially to the next, free location in the

new genome.

3. For each node pair (b, a) ∈ D with b depending on

a, do:

If all dependencies of b are satisﬁed, add b to

This operator ends when all computational nodes

have been assigned a new location in the genotype.

For better readability, we will refer to a CGP vari-

ant with the Reorder-extension as REORDER.

3 RELATED WORK

Various previous works investigated different

crossover operators for CGP and their workings.

However, to the best of our knowledge, we are the

ﬁrst to investigate the inﬂuence of the positional bias

on CGP’s crossover operator.

Cai et al. argued that CGP is not positional in-

dependent (Cai et al., 2006). This means, CGP’s

components and their workings depend on their po-

sition in the graph. As crossover does not consider

these dependencies, useful structures are destroyed.

Hence, the authors introduced a new crossover oper-

ator, which considers such dependencies. While sim-

ilar notions are made for this article, their argument

differs as they did not regard the distribution of active

nodes.

Other similar arguments to this works’ were pre-

sented by Kalkreuth et al. (Kalkreuth et al., 2017).

They argued that swapping arbitrary genes is not

preferable and introduced a subgraph-crossover oper-

ator which only recombines active nodes. However,

contrary to this work, they also did not consider the

positional bias.

Based on the just described work of Kalkreuth et

al. (Kalkreuth et al., 2017) and embedded CGP (Kauf-

mann and Platzner, 2008), Husa and Kalkreuth in-

troduced the block-crossover, which swap blocks of

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

310

consecutive active nodes (Husa and Kalkreuth, 2018;

Kalkreuth, 2020).

It is also possible to use a ﬂoating-point represen-

tation for CGP, as was done by Clegg et al. (Clegg

et al., 2007) and Wilson et al. (Wilson et al., 2018).

They tested different crossover operators and found

that their method beneﬁts from it.

In the context of image processing, Karel et al.

used the original grid-structure of CGP to evolve im-

age ﬁlters (Slan

y and Sekanina, 2007). They also

included the single-point and multi-point crossover

without modiﬁcations to CGP in their studies. By

observing the ﬁtness landscape of their solutions, the

authors concluded that the single-point crossover im-

proved the evolutionary search.

Another domain speciﬁc approach was done by

Torabi et al.. They used CGP in the context of

neural architecture search and adapted a specialized

crossover mechanism to design convolutional neural

networks (Torabi et al., ).

Some other more recent methods, such as from

Kalkreuth, developed an operator which recombines

only active nodes (Kalkreuth, 2022).

4 POSITIONAL BIAS AND

CROSSOVER

We hypothesize that the positional bias might play

a role in CGP’s issue with recombination opera-

tors. Active nodes accumulate near input nodes,

while inactive nodes concentrate near output nodes.

This means, important nodes—which generate the

output—are clustered together. However, traditional

crossover operators like the n−point or uniform

crossover do not consider such clusters. It is possible

that, by applying crossover, important semantic struc-

tures get destroyed. Other methods from Husa and

Kalkreuth (Husa and Kalkreuth, 2018), Cai et al. (Cai

et al., 2006) or Kalkreuth et al. (Kalkreuth et al., 2017)

do however consider such structures, which may be

one explanation of their performance gain.

In addition, nodes near the output nodes may also

lead to problems. They are mostly inactive, and re-

combining them should not harm the performance.

On the contrary, it should diversify the genome and

lead to more neutral genetic drift, which is a needed

trait in CGP (Turner and Miller, 2015; Yu and Miller,

2001). However, a problem might occur when active

nodes are recombined. This could completely change

the recombined phenotype, as these nodes might con-

nect to inactive nodes. These inactive nodes become

active, and connections to various other nodes might

be established. New nodes become active or inactive,

which can drastically change the phenotype.

Hence, traditional recombination operators may

lead to too much destructive behaviour for CGP. Im-

portant structures of active nodes near the input nodes

might get destroyed, while stray active nodes near the

output nodes might drastically change the phenotype.

With REORDER, the positional bias can be par-

tially circumvented. Hence, the problems stated

above could be dampened, too. As a result, REORDER

should improve with an additional crossover operator.

5 PRELIMINARY RESULTS AND

DISCUSSION

In order to get a ﬁrst grasp of REORDER’s inﬂuence

on popular, elemental crossover operators, we con-

ducted an empirical study on Boolean benchmarks. In

the following sections, we describe our experimental

design and preliminary results.

5.1 Experimental Design

We present ﬁrst results in Table 1, in which we report

three different values for each CGP variant: Its mean

number of iterations until a solution is found (I2S), its

respective standard deviation and the favourable num-

ber of computational nodes.

For our results, we tested six different CGP vari-

ants. The standard implementation described in Sec-

tion 2.1 serves as a baseline, as it is the most com-

monly found CGP implementation. In addition, a

pure REORDER variant is included as another base-

line, as four crossover operators are used with RE-

ORDER: Single-, two-, three-point- as well as a uni-

form crossover.

Each variant was trained with the Single muta-

tion. This avoids the need to optimize a mutation

rate and each variant can be compared fairer. All

variants using the crossover operator where trained

with an elitist (4 + 10)-ES, as prior work showed

that smaller population sizes are favoured (Husa and

Kalkreuth, 2018). Nonetheless, we did a hyperparam-

eter search for a good number of nodes n and tested

n ∈

{

50, 100, 150, ··· , 2000

}

. Each conﬁguration

was tested for 50 times with independent repetitions

and random seeds.

For a ﬁrst grasp, four Boolean benchmark datasets

were used: 3-bit Parity (Wegener, 2005), 16-4-bit

Encode, 4-16-bit Decode (Kaufmann and Kalkreuth,

2020) and 3-bit Multiply (White et al., 2013). For the

remainder of this work, we will refer to them as Par-

ity, Encode, Decode and Multiply respectively.

Towards Understanding Crossover for Cartesian Genetic Programming

311

Table 1: Preliminary results, showing the mean number of iterations until a solution is found (I2S) and its standard deviation,

as well as the best number of nodes found. Results for each Dataset are ordered according to their mean value.

Variant M ean(I2S) Std(I2S) # Computational Nodes

Parity

Standard (1 + 4) 342 330 600

Uniform + REORDER 437 430 50

Three-point + REORDER 678 833 50

REORDER 739 702 200

Two-point + REORDER 800 1,349 100

Single-point + REORDER 1,096 1,702 50

Encode

Three-point + REORDER 3,629 661 550

Two-point + REORDER 4,568 687 550

Uniform + REORDER 4,905 2,884 300

Standard (1 + 4) 6,213 3,368 200

Single-point + REORDER 11,927 10,500 200

REORDER 14,733 9,974 600

Decode

Uniform + REORDER 9,812 4,477 400

REORDER 15,017 10,397 700

Standard (1 + 4) 23,132 5,539 400

Two-point + REORDER 25,294 11,509 200

Three-point + REORDER 25,520 12,196 300

Single-point + REORDER 26,255 11,684 250

Multiply

Uniform + REORDER 76,117 65,594 350

REORDER 90,370 131,042 750

Standard (1 + 4) 129,739 59,127 700

Three-point + REORDER 133,506 109,385 300

Two-point + REORDER 140,705 73,147 450

Single-point + REORDER 148,384 97,937 350

All benchmarks used the same, standard ﬁtness

function for Boolean benchmarks: The ratio of cor-

rectly mapped inputs. Furthermore, we used the stan-

dard Boolean function set, containing the Boolean op-

erators AND, OR, NAND and NOR.

5.2 Discussion

As for the results shown in Table 1, some trends can

be seen.

For Parity, a standard elitist (1 + 4)–evolution

strategy performs best. However, as is argued by

White et al. (White et al., 2013), Parity is deemed

as too easy by the evolutionary algorithm community.

Hence, results from this dataset should be taken with

reservation.

As for the other three benchmarks, REORDER

with a crossover variation performs best according

to the mean I2S. Both Decode and Multiply favour

the uniform recombination, which leads to better re-

sults than both baselines. Interestingly, for these two

benchmarks, the n−point crossover performs worst.

Furthermore, single-point crossover almost always

leads to the worst results across all benchmarks. Con-

sidering the two- and three-point crossover, Encode is

the only benchmark beneﬁting from them.

We also report the best number of computational

nodes found by our hyperparameter search. However,

there is only one trend which can be read from Ta-

ble 1. REORDER in combination with a crossover op-

erator generally needs less computational nodes than

a pure REORDER variant. Considering Multiply, the

number of nodes needed is more than halved when

uniform crossover + REORDER variant is compared

to its baseline—while its mean I2S is also reduced by

about 14,000 iterations.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

312

However, it is still unclear why the uniform

crossover is preferable for Decode and Multiply,

while Encode shows different trends. Both former

benchmarks are harder benchmarks compared to En-

code and Parity, though. It is possible that the

n−point crossovers are too destructive for harder

problems, as too many useful structures are dissi-

pated. This may indicate that the positional bias

plays only a minor role in CGP’s performance with

its crossover operators. Nevertheless, we can val-

idate the results of Husa and Kalkreuth (Husa and

Kalkreuth, 2018), that different recombination oper-

ators are needed for different settings.

6 CONCLUSION

The crossover operator has been an active research

topic for Cartesian Genetic Programming (CGP)

since its introduction. To this day, it is unclear why

CGP does not generally beneﬁt from a recombination

algorithm and ﬁnding universally well-performing

operators might improve CGP’s performance greatly.

In the process to ﬁnd answers to this question,

we argued that the inﬂuence of CGP’s positional bias

might be a possible issue. The uneven distribution of

active and inactive nodes might lead to problems for

untailored crossover operators, as simply swapping

genes might destroy useful structures. To mitigate the

effects of the positional bias, the reorder extension to

CGP was reintroduced.

Our hypothesis was tested empirically and prelim-

inary results were presented. By comparing differ-

ent CGP variants with different crossover operators, a

ﬁrst conclusions can be given: The uniform crossover

generally beneﬁts CGP with reorder.

However, no clear conclusion to our hypothesis

can be drawn yet. Further evaluations and conﬁgura-

tions must be tested before the inﬂuence of the posi-

tional bias can be truly assessed. For future work, a

more diverse set of benchmarks must be tested. Test-

ing only Boolean benchmarks are not sufﬁcient and

evaluations must be extended to regression and real-

world benchmarks. Furthermore, we did not com-

pare our results to the standard CGP formula with

crossover operators, which is an important step to

assess REORDERs inﬂuence on the crossover opera-

tors. In addition, statistical analysis methods should

be added to the evaluations as well. By only compar-

ing mean values and their standard deviations, a ﬁrst

assessment can be made. However, without proper

statistical analysis, it is not possible to truly judge the

results.

Along with these evaluations mentioned, the ideas

of Kalkreuth et al. should be included (Kalkreuth

et al., 2017). By only recombining active nodes in

CGP with reorder, some effects might be observed

which could help to accept or reject our hypothesis.

Additionally, new crossover operators should be

tested to evaluate our hypothesis. New algorithms

similar to those introduced by Cai et al. could recom-

bine genes differently or with different probabilities,

based on the genes location in the graph (Cai et al.,

2006). Other operators could be inﬂuenced by exist-

ing works and be based on the density of active nodes.

Furthermore, the counts of successful crossovers,

the ﬁtness changes per crossover, distributions of ac-

tive and inactive nodes, etc. should be also accounted

for.

REFERENCES

Cai, X., Smith, S. L., and Tyrrell, A. M. (2006). Posi-

tional independence and recombination in cartesian

genetic programming. In Collet, P., Tomassini, M.,

Ebner, M., Gustafson, S., and Ek

art, A., editors, Ge-

netic Programming, pages 351–360, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Clegg, J., Walker, J. A., and Miller, J. F. (2007). A new

crossover technique for cartesian genetic program-

ming. In Annual Conference on Genetic and Evolu-

tionary Computation.

Goldman, B. W. and Punch, W. F. (2013a). Length bias

and search limitations in cartesian genetic program-

ming. In Proceedings of the 15th Annual Conference

on Genetic and Evolutionary Computation, GECCO

’13, page 933–940, New York, NY, USA. Association

for Computing Machinery.

Goldman, B. W. and Punch, W. F. (2013b). Reducing

wasted evaluations in cartesian genetic programming.

In Genetic Programming, pages 61–72, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Husa, J. and Kalkreuth, R. (2018). A comparative study

on crossover in cartesian genetic programming. In

Castelli, M., Sekanina, L., Zhang, M., Cagnoni, S.,

and Garc

ıa-S

anchez, P., editors, Genetic Program-

ming, pages 203–219, Cham. Springer International

Publishing.

Kalkreuth, R. (2020). A comprehensive study on subgraph

crossover in cartesian genetic programming. In IJCCI,

pages 59–70.

Kalkreuth, R. (2022). Towards discrete phenotypic re-

combination in cartesian genetic programming. In

Rudolph, G., Kononova, A. V., Aguirre, H., Kerschke,

P., Ochoa, G., and Tu

sar, T., editors, Parallel Prob-

lem Solving from Nature – PPSN XVII, pages 63–77,

Cham. Springer International Publishing.

Kalkreuth, R., Rudolph, G., and Droschinsky, A. (2017).

A new subgraph crossover for cartesian genetic pro-

gramming. In McDermott, J., Castelli, M., Sekanina,

Towards Understanding Crossover for Cartesian Genetic Programming

313

L., Haasdijk, E., and Garc

ıa-S

anchez, P., editors, Ge-

netic Programming, pages 294–310, Cham. Springer

International Publishing.

Kaufmann, P. and Kalkreuth, R. (2020). On the parame-

terization of cartesian genetic programming. In 2020

IEEE Congress on Evolutionary Computation (CEC),

pages 1–8.

Kaufmann, P. and Platzner, M. (2008). Advanced tech-

niques for the creation and propagation of modules

in cartesian genetic programming. In Proceedings of

the 10th Annual Conference on Genetic and Evolu-

tionary Computation, GECCO ’08, page 1219–1226,

New York, NY, USA. Association for Computing Ma-

chinery.

Langdon, W. B., Poli, R., McPhee, N. F., and Koza, J. R.

(2008). Genetic Programming: An Introduction and

Tutorial, with a Survey of Techniques and Applica-

tions, pages 927–1028. Springer Berlin Heidelberg,

Berlin, Heidelberg.

Miller, J. F. (1999). An empirical study of the efﬁciency of

learning boolean functions using a cartesian genetic

programming approach. In Proceedings of the 1st An-

nual Conference on Genetic and Evolutionary Com-

putation - Volume 2, GECCO’99, page 1135–1142,

San Francisco, CA, USA. Morgan Kaufmann Publish-

ers Inc.

Miller, J. F. (2011). Cartesian Genetic Programming.

Springer Berlin Heidelberg, Berlin, Heidelberg.

Miller, J. F. (2020). Cartesian genetic programming: its sta-

tus and future. Genetic Programming and Evolvable

Machines, 21(1):129–168.

Payne, A. J. and Stepney, S. (2009). Representation and

structural biases in cgp. In 2009 IEEE Congress on

Evolutionary Computation, pages 1064–1071.

Slan

y, K. and Sekanina, L. (2007). Fitness landscape anal-

ysis and image ﬁlter evolution using functional-level

cgp. In Ebner, M., O’Neill, M., Ek

art, A., Van-

neschi, L., and Esparcia-Alc

azar, A. I., editors, Ge-

netic Programming, pages 311–320, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Torabi, A., Shariﬁ, A., and Teshnehlab, M. Using cartesian

genetic programming approach with new crossover

technique to design convolutional neural networks.

Turner, A. J. and Miller, J. F. (2015). Neutral genetic

drift: an investigation using cartesian genetic pro-

gramming. Genetic Programming and Evolvable Ma-

chines, 16(4):531–558.

Vassilev, V. K. and Miller, J. F. (2000). The advantages

of landscape neutrality in digital circuit evolution. In

Evolvable Systems: From Biology to Hardware, pages

252–263, Berlin, Heidelberg. Springer Berlin Heidel-

berg.

Wegener, I. (2005). Complexity theory: exploring the limits

of efﬁcient algorithms. Springer Science & Business

Media.

White, D., Mcdermott, J., Castelli, M., Manzoni, L., Gold-

man, B., Kronberger, G., Ja

skowski, W., O’Reilly, U.-

M., and Luke, S. (2013). Better gp benchmarks: Com-

munity survey results and proposals. Genetic Pro-

gramming and Evolvable Machines, 14:3–29.

Wilson, D. G., Miller, J. F., Cussat-Blanc, S., and Luga,

H. (2018). Positional cartesian genetic programming.

CoRR, abs/1810.04119.

Yu, T. and Miller, J. (2001). Neutrality and the evolvability

of boolean function landscape. In Genetic Program-

ming, pages 204–217, Berlin, Heidelberg. Springer

Berlin Heidelberg.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

314