Weakly Mixing and Topological Conjugation of Discrete Dynamical

System

Jiaming Luo

1

and Mengzhu Luo

2

1

School of Mathematics and Statistics, Research Center of Modern Mathematics and Its Application, Kashi University,

Xinjiang, China

2

North China Electric Power University (Baoding), Hebei, China

Keywords: Metric Space, Weakly Mixing, Topological Conjugation.

Abstract: In this paper, by using Urysohn lemma to construct Metric space, introduce topological discrete dynamical

system, and study its weakly mixing and simple ergodicity. Moreover, by using topological conjugation

relation, the corresponding communicative condition that between measure preserving systems are given.

1 INTRODUCTION

Dynamical system describes the evolution of a point

in geometric space over time. The weakly mixing,

arbitrary order mixing and ergodic theory are the core

problems in the study of dynamic system. Especially

Rohlin's problem is an important issue that urgently

needs to be solved in this field. For example, Host

proved mixing of all orders and pairwise independent

joining of systems with singular spectrum (Host B,

1991), Kalikow proved twofold mixing implies

arbitrary mixing for rank one transformation (Host B,

1984), and Ryzhikov proved twofold mixing implies

arbitrary mixing for finite rank (Ryzhikov, V. V,

1991). This article lays the theoretical foundation for

attempting to study Rohlin's problem.

2 METRIC SPACE AND

WEAKLY MIXING OF

MEASURE PRESERVING

SYSTEM

First, the metric topological space is obtained by

constructing a given topological space and using

Urysohn lemma. Thus topological discrete dynamical

system is introduced. The weakly mixing of measure

preserving system is proved first, and several

commutative relationships of measure preserving

system are given by commutative diagrams.

Considering topological conjugation, the

corresponding communication conditions between

measure preserving systems are given.

2.1 Introduction of Measurable Space

and Probability Space

Definition 2.1.1:

Select the subsets of

0

X

to

establish a subset family

0



, then

0

X

must be the

maximum element in

0



, we have

(a)

00

X





;

(b)

0

AX

, because

0

X

is consist of the subsets

of

0

X

, so

0

A





, then

0

X

AX

derives

0

X

A





in the same way;

(c) If

1

n

BA





where

0n

A





, so

0

, 1,2,

n

A X n

and

0

1

n

AX







,

0

BX

, we

know

0

B





on the basis of the condition (b).

So

0



is a





ring of

0

X

, the

0

X

is a

measurable space. Let the measure of

0

X

be



,

00

:T X X

is also measurable. According to the

definition of the probability space, let

0

: [0,1]





and

0

( ) 1X





. We have a probability space

00

( , )X



,

.

According to the “Definition 2.1.1([

Paul R., 1974

])”

and the definition of measurable space, it be satisfied

that

Luo, J. and Luo, M.

Weakly Mixing and Topological Conjugation of Discrete Dynamical System.

DOI: 10.5220/0012285400003807

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Seminar on Artiﬁcial Intelligence, Networking and Information Technology (ANIT 2023), pages 431-436

ISBN: 978-989-758-677-4

431

1

0

, ( ) ( )A T A A

  



  

,

We have measuring system

00

( , , )XT



,

. We

need to construct and show

X

have the relationship

with

0

X

is a compact metric space in next step.

2.2 Construction of Compact Metric

Space and Introduction of Discrete

Dynamical Systems

Definition 2.1.2:

Let every single point set in

X

is

closed set. If there are two open sets contain any point

x

in

X

and a closed set

B

exclude

x

respectively,

then

X

is a regular space (Munkres J R, 2004).

Definition 2.1.3:

The topology

T

is subset family of

X

, it satisfied with these conditions:

(a)



and

X

in

T

;

(b)The union of element of any subfamily of

T

in

T

;

(c)The intersection of element of any finite

subfamily of

T

in

T

;

Then

X

is a topological space,

T

is topology of

X

(Munkres J R, 2004).

The probability space

00

( , )X



,

be satisfied

with the definition of measurable space. It is easy to

know

0



is the subfamily of

0

X

and

0

X

is the

maximum element in

0



. It is natural that

00

X





and

00

X



  

.

Now selecting any subfamily of

0

X

is

{}

i i I

A







, where

0i

AX

. According to the

condition (c) of the measurable space, we have

0i

iI

AX





, and then

0i

iI

A





. Selecting any finite

subfamily of

0



is

'

12

{ , , }

m

B B B





, where

0

, 1, ,

k

B X k m

. So

0

1

m

kk

k

B B X





, and then

0

1

m

k

B







. After simple verification, we can see

0



is

a topology of

0

X

and

00

( , )X



is a topological

space.

Choose denumerable closed sets with single point

of

0

X

:

1 2 3

{ },{ },{ }p p p

.Let

1 1 2 2 3 3

, , ,p U p U p U  

,

where

1 2 3

, , ,U U U

are the neighbourhoods of

the corresponding points and

1

i

U







.

{}

m

p

is a

single point closed set. Let the other be

1 1 1

{ }, ,{ },{ },

mm

p p p



, and

1 1 1

{ } { } { }

mm

E p p p





.

Because

1 1 1

{ }, ,{ },{ },

mm

p p p



are all

closed sets. According to the theory of topology as we

know,

E

is a closed set. Let

1 2 1 1mm

U U U U U





.

Because

, 1,2,

kk

p U k

. It is obvious that

{ } , 1,2,

kk

p U k

. By using the principle of

inclusion relation between sets,

EU

. Due to

,

ij

p p i j

, we have

m

pU

and

{}

m m m

p p U

. It is known

1

i

U







, so

m

UU

. It is obvious that

0

{ } , 1,2,

k

p X k

,

from

1 2 3 0

, , ,p p p X

and property of

neighbourhood.

Then

0

{}

mm

p U X

and

1 1 1 0mm

U U U U X





.

Let

0m

X U U X

. By the “Definition 2.1.1”,

0

X

is a regular space.

According to the previous discussion, it is known

that

0

XX

and

0

X

is a topological space. By

Using inherited principle of topological space,

X

is

also a regular space. The topology

T

of

X

is

determined at the same time.

Theorem 2.1.4:

Let

X

is a topological space. is

a subfamily of open sets of

X

. For any open set

U

of

X

and any point

xU

, an element

C

of

existed, Such that

x C U

. Then is a basis on

the topology of

X

(Munkres J R, 2004).

It is known that the topological space

X

is a

measurable space. We need to prove that any open set

U

of

X

be corresponding to denumerable open

subsets

12

,,CC

, such that

1

i

UC





and

1

i

C







.

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

432

It is obvious that open set

UX

be equal to

union of disjoint subsets, I. e.

1

i

UD





and

1

i

D







. If

l

D

is a closed set, the others are open

sets. There be an open set

l

C

such that

ll

DC

. It

is evident that

l

C

could have intersection with some

disjoint open sets, i. e.

, 1,2,

k

li

C D k  

.

According to the theory of topology as we know,

the finite intersection of open sets is the open set. We

can have denumerable disjoint open sets

12

,,CC

by rearranging

( ), 1,2,

kk

i l i

D C D k

and

the rest of open sets, such that

1

i

UC





. If non-open

sets

12

,,

jj

DD

exists, we can find open sets

12

,,

jj

CC

have intersection with some disjoint

open sets by same way. I. e.

(1) (2)

12

, , , 1,2,

kk

jj

nn

C D C D k    

.

By the same reason

，

(1) (2)

12

, , , 1,2,

kk

jj

nn

C D C D k 

are open sets. We can have denumerable disjoint open

sets

12

,,CC

by rearranging

(1) (1) (2) (2)

12

( ), ( ), , 1,2,

k k k k

jj

n n n n

D C D D C D k  

and the rest of open sets, such that

1

i

UC





. So this

problem has been proved.

It is necessary to construct the denumerable open

set family

：

Situation i: If

X

has the only one open set

U

,

aforementioned

12

,,CC

can be regarded as the

elements of . I. e.

12

{ , , }CC

is a

denumerable family;

Situation ii: If

X

has two open sets

,UV

, by the

previous mentioned method about

V

to get

1

i

VD





, where

i

D

is in accordance with

i

C

，

1,2,i 

. I. e.

1 1 2 2

{ , , , , }C D C D

is a

denumerable family by the arrangement principle of

denumerable sets;

Situation iii: If

X

has the denumerable open sets

12

,,UU

，

let

(1) (2)

12

11

, , ,

ii

U C U C





where

()

, , 1,2,

j

i

C i j 

has the same definition with

situation i and situation ii.

Make the following arrangement (I P. Natanson,

2016):

(1) (1) (1)

1 2 3

(2) (2) (2)

1 2 3

(3) (3) (3)

1 2 3

,,,

CCC













.

Put the elements with the same superscript plus

subscript together to correspond to the elements of

N

and rearrange them. We have

(1) (1) (2) (1) (2) (3) (1)

1 2 1 3 2 1 4

{ , , , , , , , }C C C C C C C N

.

It is obvious that is denumerable.

The above is the ideal situation, that is to say,

denumerable open subsets of

X

satisfy

1

i

U







.

If

1

i

U







, we can take all of open sets as a whole.

And then the detail process is similar to the situation

i. If some terms

12

, , ,

n

i i i

U U U

have intersection,

we can think of these terms as a whole and rearrange

them. The result of the rearrangement will not change.

In conclusion, is a denumerable family.

Assume that

1 2 3

{ , , , }A A A

, where

i

A

always be contained in some open sets of

X

. For any

open set

V

of

X

, we have

1

i

k

i

VA





. According to

the previous discussion, we have

1

i

k

i

A







, where

, 1,2,

i

k

A V i

. So for any point

xV

, we

always find some

m

k

A

such that

m

k

x A V

.

Because

m

k

A 

is known, so is denumerable

basis of topology

T

of

X

by introduction of

theorem 1. Therefore regular space

X

has the

denumerable basis.

Theorem 2.1.5:

(Urysohn) Every regular space

X

with the denumerable basis is a metric space

(Munkres J R, 2004).

By the “Theorem 2.1.5”, we have the condition (I):

Topological space

X

is a metric space.

According to above discussion (topology space

X

has the denumerable base) and the second axiom

Weakly Mixing and Topological Conjugation of Discrete Dynamical System

433

of countability, we have

X

is a second denumerable

space. Because the second denumerable space is the

separable Lindelof space by topological theory as we

know. So we have condition (II):

X

is a compact

space. According to condition (I) and condition (II),

topological space

X

is a compact metric space.

Considering the situation in question, so let

.

( , ) ( , ) max , ,

X

x y d x y x y x y X



    

Because

X

is a compact metric space, we can

definite the self-action

:T X X

on

X

.The

topology discrete dynamic system is introduced

：

1 0 1

{ , , , , , , , }

nn

T T T T T



.

(Note: Let

0

()CX

be the collection of all

consecutive self-mappings of

X

, then

0

()T C X

.

( , )XT

represents compact system which be

generated by continuous self-mapping

T

of compact

metric space

X

.)

2.3 Weakly Mixing and Commutativity

of Measure Preserving System

Since

00

( , , )X



is a probability space by the

section 2.1. Due to

0

XX

,

( , , )X



is also a

probability space. Because

00

( , , )X



is a

measurable space,

( , , )X



is obviously a

measurable space. Therefore the measure preserving

system

( , , , )XT



can be used as the research

object.

Considering that measure preserving system

( , , , )XT



is weakly mixing, we have these

conditions:

1)

T

is topological weakly mixed;

2) measure preserving system

( , , , )XT



is

ergodic;

3)

( , , , ) ( , , , )X T X T

   



is ergodic.

Condition 2) can be launched: if self-mapping

T

is

a measure-preserving map,



is a invariant measure,



is ergodic, for

B





, we have

1

()T B B







( ) 1B





or

( ) 0B





。

The first description of independence about

,ABX

under the known conditions:

Because

{}nJ

is sequence with density 1

，

and



is ergodic. When

1n 

, we have

B

with

1

()T B B





or

A

with

1

()T A A





. According

to relevant definitions, it is known that

1

( ) ( )A T B A B







. So we have

( ) 1B





or

( ) 0B





.

If

( ) 1B





, then

( ) ( ) ( ) ( )A B A A B

   



;

If

( ) 0B





, then

( ) ( ) ( ) ( )A B B A B

   



.

( ) ( ) ( )A B A B

  



is right. Therefore the

independence about any

,AB





is right under the

known conditions. Let

()

A

AB

B

A





, so

( ) ( )

A

BB





.

We need to build the exchange relationship

between measurable spaces:

Let

Y

is a interval of real number field

R

.

Assuming that





ring

A

is made of subsets of

Y

.

According to the definition of measurable space, we

can construct measurable space

( , , )Y MA

, where

measure

M

is a mapping, i. e.

 

: 0,1R M

.

M

has the following properties (I P. Natanson,

2016):

1)

( ) 0M

；

2)

,

ij

i j A A   

, where

, 1,2

i

AiA

；

3)

1

( ) ( )

nn

n

AA







MM

under condition 1) and

condition 2).

Let

Y

be satisfied with

( ) 1Y M

, we have the

probability space

( , , )Y MA

. According to the

“Definition 2.1.1”,

( , , )Y MA

is a metric space.

The continuous self-mapping

:S Y Y

can be

established. Because

1

, ( )A S A



  AA

, so

1

:S Y Y





is a continuous self-mapping. The

topological discrete dynamical system is introduced

by

1 0 1

{ , , , , , , , }

nn

S S S S S



.

Because

( , , )Y MA

is a measurable space. So

:S Y Y

and

1

:S Y Y





are measurable by the

definition of measurable space. Thus

AA

，

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

434

1

:

A

S A A





is measurable. As a result of

1

S A A





, we have

1

( ) ( )S A A



MM

. (1)

Because

1

:

A

S A A





is measurable,

:

A

S A A

is also measurable and

SA A

. We have

1 1 1 1

( ) ( ) ( ( )) ( )A S S A S A A S S A S A

   

    M M M

.

(2)

1

( ) ( )S A A



MM

can be got from formula (1)

and formula (2). So

:S Y Y

is measure-

preserving,

M

is invariant measure of

S

.

Therefore measure preserving system

( , , )YSM,A

is ergodic, where

M

is ergodic.

Let

: XY

be continuous mapping.

Because

( , )X



X,

and

( , , )Y M,A

are metric

spaces. Assuming that the metric of

X

is

1



and the

metric of

Y

is

2



, then

0, ,x y X



  

, exists

0





, such that

12

( , ) ( ( ), ( ))x y x y

   

    

.

In a similar way,

0, ,w z Y



  

, exists

0





,

such that

11

21

( , ) ( ( ), ( ))w z w z

   



    

.

1

:YX





is a continuous mapping, thus



is

homeomorphism mapping. Considering the

following conditions:

1)

( , , )YSM,A

is measure preserving and

ergodic;

2)



is homeomorphism mapping;

3)

 

: 0,1X





and

 

: 0,1Y M

are finite

measures;

4)

( , )XT

and

( , )YS

are compact systems.

We have the following commutative diagrams:

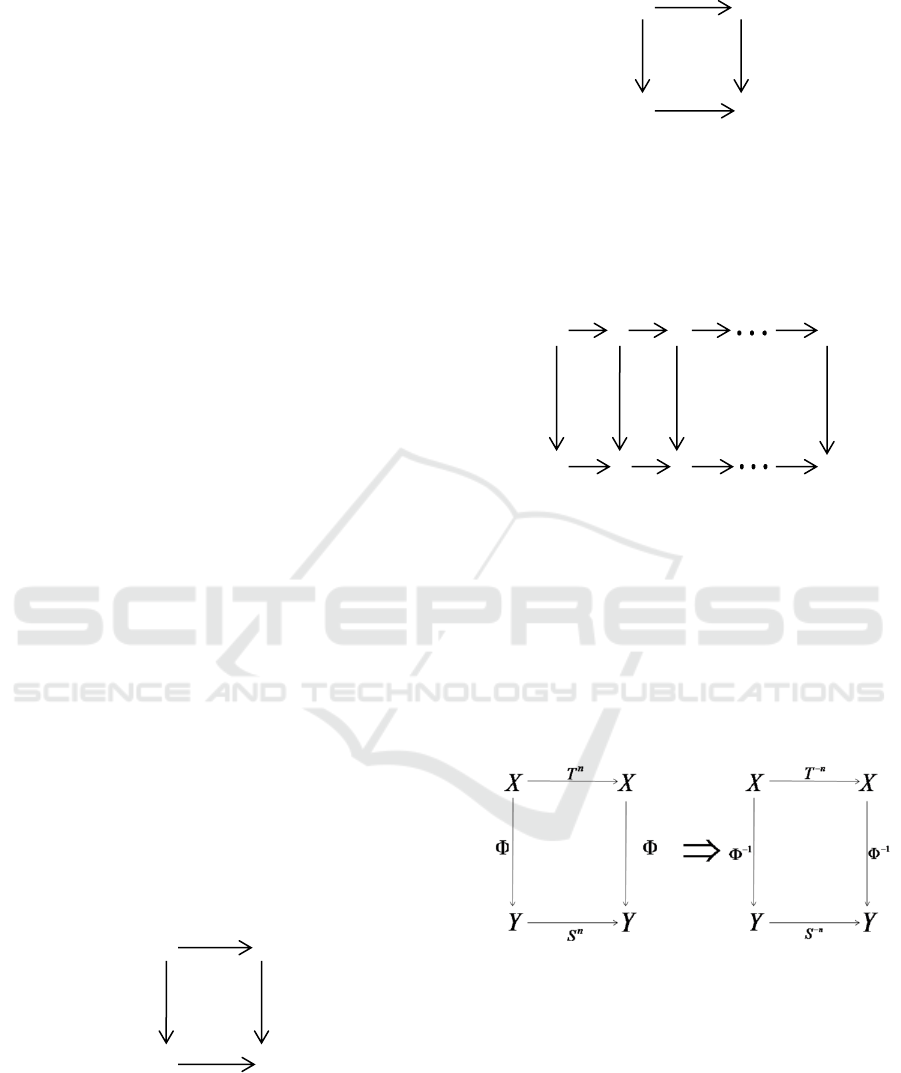
Figure 1. The commutative diagram of probability spaces.

.

Figure 2. The commutative diagram of measure preserving

systems.

We have

=ST

by the figure 2, where



is

topological conjugate from

T

to

S

. The figure 2

implies the figure 3:

.

Figure 3. The finite order commutative diagram of measure

preserving systems.

We have

=

nn

ST

by figure 3, where



is

topological conjugate from

n

T

to

n

S

. In a similar

way,

0n

，

1



is topological conjugate from

S

to

T

,

1



is topological conjugate from

n

S



to

n

T



. Therefore we have the following figure:

.

Figure 4: (a). The merge commutative diagram. (b). The

inverse mapping commutative diagram.

The figure 1 implies



=M

, the figure 4(a) and

4(b) imply that

nn

TS



  

, let it be called by

corresponding commutative condition.

X

Y



[0,1]

M

i



X

Y

T

S



X

T

Y

S



Weakly Mixing and Topological Conjugation of Discrete Dynamical System

435

3 CONCLUSION

By constructing a given topological space and using

Urysohn lemma, a metric topological space is

obtained. On this basis, topological discrete

dynamical system is introduced, weakly mixing of

measure preserving system has been proved, and

several commutative relationships of measure

preserving systems are given. By using topological

conjugation, the corresponding communicative

condition that between measure preserving systems

are given. In the future, more in-depth research is

needed on the arbitrary mixing and ergodicity of

discrete dynamical system. The application of mixing

and complex ergodicity of discrete dynamical system

in Markov chain is also an important research

direction in the next step.

REFERENCES

Host B, Mixing of all orders and pairwise independent

joinings of systems with singular spectrum [J], Israel

Journal of Mathematics, 1991, 76(3): 289-298.

https://doi.org/10.1007/BF02773866.

Kalikow, Arthur S, Twofold mixing implies threefold

mixing for rank one transformations[J], Ergodic Theory

& Dynamical Systems, 1984, 4(02): 237-259.

https://doi.org/10.1017/S014338570000242X.

Ryzhikov, V. V, Joinings of dynamical systems.

Approximations and mixing [J], Russian Mathematical

Surveys, 1991, 46(5): 199-200.

https://doi.org/10.1070/RM1991v046n05ABEH002848

Paul R. Halmos, Measure Theory [M], New York,

Springer-Verlag, 1974, 15-183.

Munkres J R, Topology [M], China Machine Press, 2004,

23-210.

I P. Natanson, Theory of Functions of a Real Variable [M],

New York, Dover Publications, 2016, 18-102.

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

436