
NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL
SMOOTHER WITH CORRELATED UNCERTAIN OBSERVATIONS
S. Nakamori
Department of Technology. Faculty of Education, Kagoshima University
1-20-6, Kohrimoto, Kagoshima 890-0065, Japan
R. Caballero-
´
Aguila
Departamento de Estad
´
ıstica e Investigaci
´
on Operativa, Universidad de Ja
´
en
Paraje Las Lagunillas, s/n, 23071 Ja
´
en, Spain
A. Hermoso-Carazo and J. Linares-P
´
erez
Departamento de Estad
´
ıstica e Investigaci
´
on Operativa, Universidad de Granada
Campus Fuentenueva, s/n, 18071 Granada, Spain
Keywords:
Least-squares estimation, filtering, fixed-interval smoothing, uncertain observations
Abstract:
A least-squares linear fixed-interval smoothing algorithm is derived to estimate signals from uncertain obser-
vations perturbed by additive white noise. It is assumed that the Bernoulli variables describing the uncertainty
are only correlated at consecutive time instants. The marginal distribution of each of these variables, specified
by the probability that the signal exists at each observation, as well as their correlation function, are known.
The algorithm is obtained without requiring the state-space model generating the signal, but just the covariance
functions of the signal and the additive noise in the observation equation.
1 INTRODUCTION
The problem of estimating a discrete-time signal from
noisy observations in which the signal can be ran-
domly missing is considered. To describe this situa-
tion, the observation equation is formulated multiply-
ing the signal at any sample time by a binary random
variable taking the values one and zero. So, the obser-
vation equation involves both an additive and a mul-
tiplicative noise which models the uncertainty about
the signal being present or missing at each observa-
tion. It is assumed that, for each particular observa-
tion, the probability of containing the signal is known
for the observer.
In many practical situations, the variables mod-
elling the uncertainty in the observations can be as-
sumed to be independent and, then, the distribution
of the multiplicative noise is fully determined by
the probability that each particular observation con-
tains the signal. A different situation, in which the
variables modelling the uncertainty are correlated at
consecutive instants, is considered by Jackson and
Murthy (1976) who, using a state-space approach, de-
rived a least-squares linear filtering algorithm which
allows to obtain the signal estimator at any time from
those in the two preceding instants.
In the last years, the estimation problem in the
aforementioned situations has been investigated under
a more general approach which does not require the
state-space model, but only the autocovariance func-
tion of the signal. Assuming that this function can
be expressed in a semi-degenerate kernel form, algo-
rithms with a simpler structure than the correspond-
ing ones when the state-space model is known have
been obtained for different estimation problems (see
Nakamori et al. (2003a) for the linear filter and fixed-
point smoother when the uncertainty is modelled by
independent random variables). The situation con-
sidered by Jackson and Murthy (1976) has been also
treated in Nakamori et al. (2003b) under a covariance
approach and filtering and fixed-point smoothing al-
gorithms have been derived for this uncertain obser-
vation model. The aim in this paper is to propose a
fixed-interval smoothing algorithm based on covari-
ance information for this last model.
The fixed-interval smoothing problem appears
when all the measurements of the signal inside a time-
interval are available before proceeding to the esti-
mation. Fixed-interval smoothing techniques have
been applied to stochastic signal processing problems
203
Nakamori S., Caballero-Águila R., Hermoso-Carazo A. and Linares-Pérez J. (2004).
NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL SMOOTHER WITH CORRELATED UNCERTAIN OBSERVATIONS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 203-207
DOI: 10.5220/0001125702030207
Copyright
c
SciTePress

(Ferrari-Trecate and De Nicolao, 2001, Young and
Pedregal, 1999) as well as to the estimation of time-
variable parameters (Young et al., 2001).
In this paper we treat the least-squares linear
estimation problem and the fixed-interval smooth-
ing algorithm is derived under an innovation ap-
proach. This approach provides an expression for the
smoother as the sum of the filter and another term,
uncorrelated with it, which can be obtained from a
backward-time algorithm.
The filtering and fixed-interval smoothing algo-
rithms are applied to a simulated observation model
where the signal cannot be missing in two consecutive
observations, situation which can be covered by the
correlation form considered in the theoretical study.
2 ESTIMATION PROBLEM
We consider the least-squares (LS) linear estimation
problem of a discrete-time signal from noisy uncer-
tain observations described by
y(k) = θ(k)z(k) + v(k) (1)
where the involved processes satisfy:
(I) The signal process {z(k); k ≥ 0} has zero mean
and its autocovariance function is expressed in a semi-
degenerate kernel form, that is,
K
z
(k, s)=E[z(k)z
T
(s)]=
½
A(k)B
T
(s), 0 ≤ s ≤ k
B(k)A
T
(s), 0 ≤ k ≤ s
where A and B are known n × M
0
matrix functions.
(II) The noise process {v(k); k ≥ 0} is a zero-mean
white sequence with known autocovariance function,
E[v(k)v
T
(s)] = R
v
(k)δ
K
(k − s).
(III) The multiplicative noise {θ(k); k ≥ 0}
is a sequence of Bernoulli random variables with
P [θ(k) = 1] =
θ(k) and autocovariance function
K
θ
(k, s) =
½
0, |k − s| ≥ 2
E[θ(k)θ(s)] − θ(k)θ(s), |k − s| < 2
(IV) The processes {z(k); k ≥ 0}, {v(k); k ≥ 0}
and {θ(k); k ≥ 0} are mutually independent.
The purpose is to obtain a fixed-interval smooth-
ing algorithm; concretely, assuming that the obser-
vations up to a certain time L are available, our
aim is to find recursive formulas which allow to ob-
tain the estimators of the signal, z(k), at any time
k ≤ L. For this purpose, we will use an innova-
tion approach. If by(k, k − 1) denotes the LS lin-
ear estimator of y(k) based on {y(1), . . . , y(k − 1)},
ν(k) = y(k) − by(k, k − 1) represents the innova-
tion contained in the observation y(k), that is, the
new information provided by y(k) after its estima-
tion from the previous observations. It is known that
the LS linear estimator of z(k) based on the observa-
tions {y(1), . . . , y(L)}, which is denoted by bz(k, L),
is equal to the LS linear estimator based on the in-
novations {ν(1), . . . , ν(L)}. The advantage of con-
sidering the innovation approach to address the LS
estimation problem comes from the fact that the in-
novations constitute a white process; then, by denot-
ing Π(i) = E[ν(i)ν
T
(i)], the Orthogonal Projection
Lemma (OPL) leads to
bz(k, L) =
L
X
i=1
E[z(k)ν
T
(i)]Π
−1
(i)ν(i). (2)
In view of (2), the first step to obtain the estimators
is to establish an explicit formula for the innovations,
which is presented in Theorem 1. Afterwards, in the
next section, we present recursive formulas for the
fixed-interval smoother, bz(k, L), k < L, including
that of the filter, bz(k, k). These formulas have been
derived by decomposing (2) as the filter and a correc-
tion term uncorrelated with it, and obtaining recursive
expressions for both terms from the OPL.
2.1 Innovation process
When the variables {θ(k); k ≥ 0} modelling the un-
certainty are independent all the information prior to
time k which is required to estimate y(k) is provided
by the one-stage predictor of the signal, bz(k, k − 1).
However, for the problem at hand, the correlation be-
tween θ(k − 1) and θ(k), which must be considered
to estimate y(k), is not contained in bz(k, k − 1). Con-
cretely, as it is indicated in Theorem 1, in this case the
innovation is obtained by a linear combination of the
new observation, the predictor of the signal and the
previous innovation.
Theorem 1. Under hypotheses (I)-(IV), the innova-
tion process associated with the observations given in
(1) satisfies
ν(k) = y(k)−
θ(k)A(k)O(k − 1)−K
θ
(k, k − 1)
×A(k)B
T
(k−1)Π
−1
(k−1)ν(k −1), k ≥ 2
ν(1) = y(1)
where the vectors O(k) are calculated from
O(k) = O(k − 1) + J(k)Π
−1
(k)ν(k), k ≥ 1
O(0) = 0
being
J(k) = θ(k)
£
B
T
(k)−r(k −1)A
T
(k)
¤
−K
θ
(k, k−1)
×J(k−1)Π
−1
(k−1)B(k −1)A
T
(k), k ≥ 2
J(1) = θ(1)B
T
(1)
and Π(k) the covariance matrix of the innovation,
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
204

which is given by
Π(k) = θ(k)A(k)
£
B
T
(k) − θ(k)r(k − 1)A
T
(k)
¤
−K
2
θ
(k, k − 1)A(k)B
T
(k − 1)
×Π
−1
(k − 1)B(k − 1)A
T
(k)
−
θ(k)K
θ
(k, k − 1)A(k)
h
J(k − 1)
×Π
−1
(k − 1)B(k − 1) + B
T
(k − 1)
×Π
−1
(k − 1)J
T
(k − 1)
i
A
T
(k) + R
v
(k).
The covariance r(k) of the vector O(k) verifies
r(k) = r(k − 1) + J(k)Π
−1
(k)J
T
(k), k ≥ 1
r(0) = 0.
3 FIXED-INTERVAL SMOOTHER
Theorem 2. Assuming hypotheses (I)-(IV), the es-
timators of the signal z(k) from the observations
y(1), · · · , y(L), with k ≤ L, are given by
bz(k, L) = bz(k, k) + [B(k) − A(k)r(k)]q
1
(k, L)
+A(k)J(k)q
2
(k, L), k < L
bz(k, k) = A(k)O(k), k ≤ L
where q
1
(k, L) and q
2
(k, L) can be recursively calcu-
lated, from q
1
(L, L) = 0 and q
2
(L, L) = 0, by
q
1
(k, L)=
£
I
M
0
−∆
1
(k+1)Π
−1
(k+1)J
T
(k+1)
¤
×q
1
(k + 1, L) + ∆
1
(k+1)q
2
(k + 1, L)
+∆
1
(k+1)Π
−1
(k+1)ν(k +1), k < L
q
2
(k, L) = −∆
2
(k+1)Π
−1
(k+1)J
T
(k + 1)
×q
1
(k + 1, L) + ∆
2
(k+1)q
2
(k+1, L)
+∆
2
(k+1)Π
−1
(k+1)ν(k +1), k < L
with
∆
1
(k + 1) =
θ(k + 1)A
T
(k + 1),
∆
2
(k + 1)=−K
θ
(k+1, k)Π
−1
(k)B(k)A
T
(k + 1).
3.1 Error covariance matrices
The LS method uses the covariance matrices,
P (k, L), of the estimation errors to measure the good-
ness of the estimators. It is easy to verify that
P (k, L) = K
z
(k, k) − E[bz(k, L)bz
T
(k, L)].
Hence, using the expression given in Theorem 2 for
bz(k, L) and the uncorrelation property between each
q
s
(k, L), s = 1, 2, and bz(k, k) we have
P (k, L) = P (k, k) − [B(k) − A(k)r(k)]Q
1
(k, L)
×[B(k) − A(k)r(k)]
T
−A(k)J(k)Q
2
(k, L)J
T
(k)A
T
(k)
−[B(k) − A(k)r(k)]Q
12
(k, L)J
T
(k)A
T
(k)
−A(k)J(k)Q
T
12
(k, L)[B(k) − A(k)r(k)]
T
where P (k, k), the filtering error covariance matrix,
is given by
P (k, k) = A(k)
£
B
T
(k) − r(k)A
T
(k)
¤
, k ≤ L.
The matrices Q
s
(k, L), for s = 1, 2, and Q
12
(k, L)
are obtained by
Q
1
(k, L) =F (k + 1)Q
1
(k + 1, L)F
T
(k + 1)
+∆
1
(k + 1)
£
Q
2
(k + 1, L) + Π
−1
(k + 1)
¤
×∆
T
1
(k + 1)+F (k + 1)Q
12
(k + 1, L)∆
T
1
(k + 1)
+∆
1
(k + 1)Q
T
12
(k + 1, L)F
T
(k + 1)
Q
2
(k, L) =∆
2
(k + 1)Π
−1
(k + 1)
£
J
T
(k + 1)
×Q
1
(k + 1, L)J(k + 1) + Π(k + 1)] Π
−1
(k + 1)
×∆
T
2
(k + 1) + ∆
2
(k + 1)Q
2
(k + 1, L)∆
T
2
(k + 1)
−∆
2
(k + 1)Π
−1
(k + 1)J
T
(k + 1)Q
12
(k + 1, L)
×∆
T
2
(k + 1) − ∆
2
(k + 1)Q
T
12
(k + 1, L)J(k + 1)
×Π
−1
(k + 1)∆
T
2
(k + 1)
Q
12
(k, L) =−F (k + 1)Q
1
(k + 1, L)J(k + 1)
×Π
−1
(k + 1)∆
T
2
(k + 1)+∆
1
(k + 1)Q
2
(k + 1, L)
×∆
T
2
(k + 1)+F (k + 1)Q
12
(k+1, L)∆
T
2
(k, k+1)
−∆
1
(k + 1)Q
T
12
(k + 1, L)J(k + 1)Π
−1
(k + 1)
×∆
T
2
(k + 1) + ∆
1
(k + 1)Π
−1
(k + 1)∆
T
2
(k + 1)
for k < L, with initial conditions Q
s
(L, L) = 0, for
s = 1, 2, and Q
12
(L, L) = 0, being
F (k + 1) = I
M
0
−∆
1
(k + 1)Π
−1
(k + 1)J
T
(k + 1).
4 COMPUTER RESULTS
We consider a sequence of independent Bernoulli ran-
dom variables, {γ(k); k ≥ 0}, taking the value one
with probability p and we define
θ(k) = 1 − γ(k − 1) + γ(k − 1)γ(k), k ≥ 1.
So, the variables θ(k) are also Bernoulli random vari-
ables and, since θ(k) and θ(s) are independent for
|k −s| ≥ 2, they are uncorrelated and hypothesis (III)
is satisfied. The common mean of these variables is
θ = 1 − p + p
2
and its covariance function is given by
K
θ
(k, s) =
½
0, |k − s| ≥ 2
−(1 − θ)
2
, |k − s| < 2
Let z(k) be the signal to be estimated and y(k) the
observation of this signal, defined as in (1) by
y(k) = θ(k)z(k) + v(k)
where v(k) represents the measurement noise.
Since θ(k) = 0 corresponds to γ(k − 1) = 1 and
γ(k) = 0, this fact implies that θ(k + 1) = 1 and,
hence, the possibility of the signal being missing in
two successive observations is avoided. So, the con-
sidered observation model covers those signal trans-
mission models with stand-by sensors, in which any
NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL SMOOTHER WITH CORRELATED UNCERTAIN
OBSERVATIONS
205
failure in the transmission is immediately detected
and the old sensor is then replaced.
We have assumed that the autocovariance function
of the signal is
K
z
(k, s) = 1.025641 × 0.95
k−s
, 0 ≤ s ≤ k.
The noise {v(k); k ≥ 0} has been assumed to be a
sequence of independent random variables with
E[v(k)] = 0, R
v
(k) = 0.7037037.
To show the effectiveness of the algorithm pro-
posed in this paper, we compare the results obtained
from 100 observations of the signal, using different
values of the parameter p.
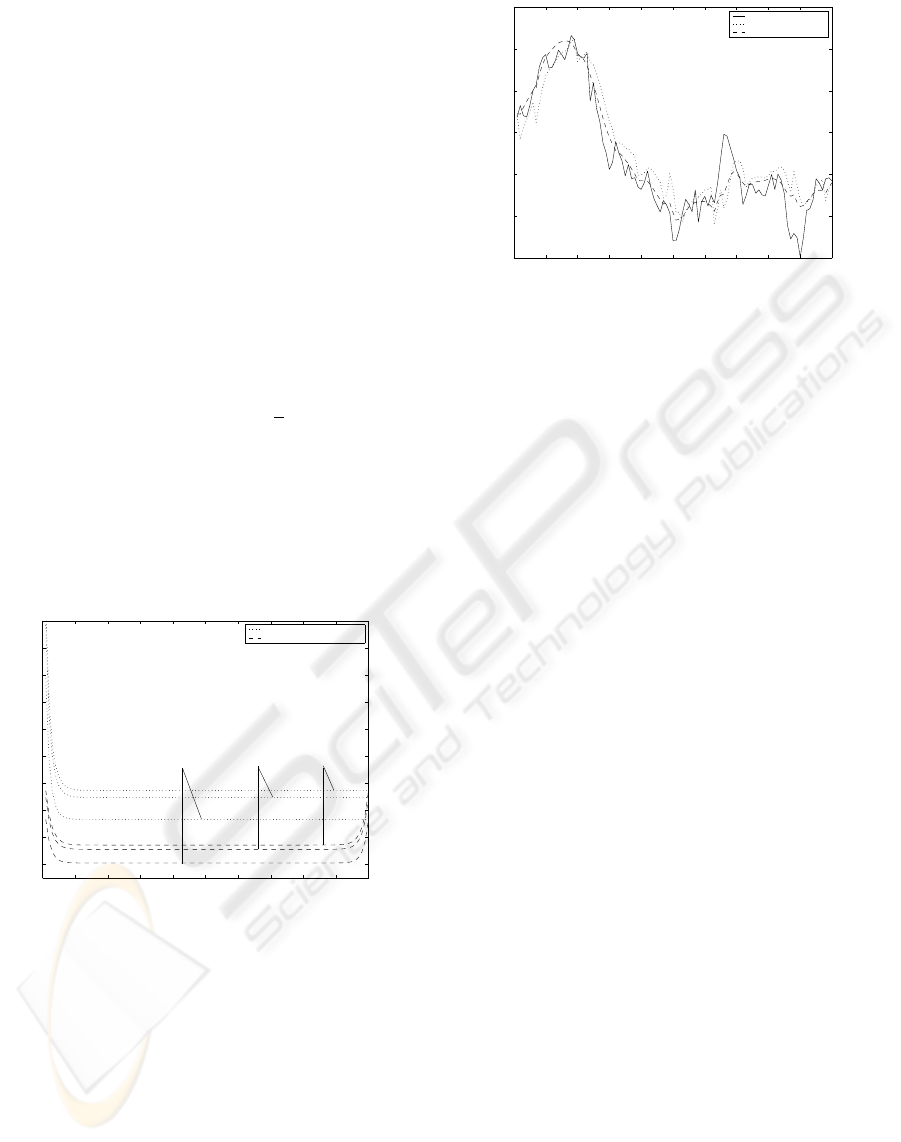
First, the performance of the filter and fixed-
interval smoother, measured by the error variances,
has been calculated for p = 0.1, 0.3 and 0.5. The
results are displayed in Figure 1 which shows that the
estimators have a better performance as p is smaller,
due to the fact that the mean value, θ, decreases with
p. Moreover, this figure shows not only that, for
each value of p, the error variances are smaller us-
ing the fixed-interval smoother instead of the filter,
but also that the improvement with the smoother is
highly significant since, even the worst results with
the smoother (p = 0.5) are better than the best ones
with the filter (p = 0.1). A simulated signal and
0 10 20 30 40 50 60 70 80 90 100
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
Time k
Filtering error variances
Fixed−interval error variances
p=0.5
p=0.3
p=0.1
Figure 1: Filtering and fixed-interval smoothing error vari-
ances for p = 0.1, 0.3, 0.5.
their filtered and smoothed estimates from 100 ob-
servations simulated with p = 0.1 are displayed in
Figure 2. The result, as expected, is that the smooth-
ing estimates are nearer to the signal and, hence, the
behaviour of the fixed-interval smoother is better than
that of the filter.
5 CONCLUSION
In this paper, the LS linear fixed-interval smoother is
derived from uncertain observations of a signal, when
0 10 20 30 40 50 60 70 80 90 100
−3
−2
−1
0
1
2
3
Time k
Signal
Filter
Fixed−interval smoother
Figure 2: Signal, filtering and fixed-interval smoothing es-
timates for p = 0.1.
the Bernoulli random variables characterizing the un-
certainty in the observations are correlated at consec-
utive time instants, for the case of white observation
additive noise. It is not required the knowledge of the
state-space model, but only the covariance matrices
of the processes involved in the observation equation.
The recursive algorithms are derived by an innovation
approach.
The results are applied to a particular model which
includes signal transmission models with stand-by
sensors for the immediate replacement of a failed unit.
ACKNOWLEDGMENT
Supported by the ‘Ministerio de Ciencia y Tec-
nolog
´
ıa’. Contract BFM2002-00932.
REFERENCES
Young, P. and Pedregal, D. (1999). Recursive and en-bloc
approaches to signal extraction. Journal of Applied
Statistics, 26(1):103–128.
Ferrari-Trecate, G. and De Nicolao, G. (2001). Computing
the equivalent number of parameters of fixed-interval
smoothers. In Proc. 40th IEEE Conf. on Decision and
Control, volume 3, pages 2905–2910.
Jackson, R. N. and Murthy, D. N. P. (1976). Optimal linear
estimation with uncertain observations. IEEE Trans-
actions on Information Theory, May:376–378.
Nakamori, S., Caballero, R., Hermoso, A. and Linares, J.
(2003a). Linear estimation from uncertain observa-
tios with white plus coloured noises using covariance
information. Digital Signal Processing, 13:552–568.
Nakamori, S., Caballero, R., Hermoso, A. and Linares, J.
(2003b). New linear estimations from correlated un-
certain observations using covariance information. In
Proc. Twelfth IASTED Conf. ASM, pages 295–300.
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
206

Young, P. C., McKenna, P. and Bruun, J. (2001). Identi-
fication of non-linear stochastic systems by state de-
pendent parameter estimation. International Journal
of Control, 74:1837–1857.
NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL SMOOTHER WITH CORRELATED UNCERTAIN
OBSERVATIONS
207
