
DECENTRALIZED ESTIMATION FOR AGC OF POWER
SYSTEMS
Xue-Bo Chen
School of Electronic & Information Engineering, Anshan University of Science & Technology, Anshan 114044, P. R. China
Xiaohua Li
School of Information Science and Engineering, Northeast University, Shenyang 110004, P. R. China
Srdjan S. Stankovic
University of Belgrade, Belgrade 11000, Yugoslavia
Keywords: Decentralized estimation, Inclusion principle, Automatic generation control
Abstract: A decentralized state estimation
method for automatic generation control (AGC) of interconnected power
systems is proposed in this paper. Based on the Inclusion Principle for linear stochastic systems, the state
space model of the system is decomposed as a group of pair-wise subsystem models. The overlapping
decentralized estimators and fully decentralized estimators are designed for each pair subsystems in the
framework of LQG control schemes. Two types of estimators are considered for the cases of full and
reduced measurement sets in the framework of system closed-loop operations. Simulation results show a
high quality of the AGC scheme based on dynamic controllers with the proposed state estimators.
1 INTRODUCTION
Generally speaking, in power system models, an
overall system with a longitudinal or a loop or a
radial or a network structure can be divided into a lot
of overlapping interconnected subsystems. Tie line
powers, i.e. the sine of the voltage phase angle
differences at the two ends of tie lines connected
with areas, are the interconnections of the
subsystems. It has been found that the decentralized
controllers could be designed based only on local
measurements, especially, the tie line power
between each pair of areas and the frequency in each
area (Chen, 1994; Ohtsuka and Morioka, 1997;
Stankovic et al., 1999). Although the decentralized
control for overlapping interconnected power
systems has attracted considerable attention of
researchers (Chen, 1994; Chen and Stankovic, 1996;
Ikeda et al., 1981; Malik and Hope, 1984/1985;
Ohtsuka and Morioka, 1997; Park and Lee, 1984;
Siljak, 1978 and 1991; Stankovic et al., 1999), the
decentralized state estimation has been treated
mostly within the framework of the dynamic
controllers. The estimators of Kalman filter type are
discussed in (Hodzic and Siljak, 1986), while in
(Ikeda and Siljak, 1986) deterministic systems and
their observers are considered in the case of the
contractibility of dynamic controllers. The inclusion
of observers for deterministic systems has been
considered in (lftar, 1993). Luenberger observers are
considered in (Park and Lee, 1984) separately with
the near optimal decentralized control, since the tie-
line power flow deviations are treated as the
interconnecting states noted as relatively slow.
However, from the practical feasibility point of view,
the area autonomy and decentralized estimator
design of the power system has not been mature.
First of all in this paper, a kind of multi-
ove
rlapping interconnected power system model is
decomposed as a group of pair-wise areas and/or
subsystems (Chen et al., 2002) with only one
overlapping interconnection (the tie-line power)
between the two subsystems. Then, the inclusion of
Kalman filter type estimators is formulated for the
subsystem AGC. Finally, starting from a pair of
electric power subsystems, overlapping and fully
decentralized estimators based on full and reduced
257
Chen X., Li X. and Stankovic S. (2004).
DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 257-263
DOI: 10.5220/0001126402570263
Copyright
c
SciTePress

measurement sets are formulated. The fully
decentralized scheme used only local area
measurements is based on a separate tie-line power
estimator. Experimental results illustrate the main
features of the proposed estimators applied to AGC.
2 SYSTEM MODEL STRUCTURES
Consider a power system with multi- overlapping
interconnected structures (Siljak, 1978), described
by the linear stochastic continuous-time dynamic
model as follows:
⎪
⎩
⎪
⎨
⎧
,
,
,1
iiii
N
ijj
jijiiiiiii
xCy
xAuBxAx
η
ξ
+=
+Γ++=
∑
≠=
&
i = 1, 2, …, N, (1)
where,
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
∑
≠=
00
10
0
,1
1
N
ijj
T
iji
T
i
tiii
i
m
d
aA
A
α
,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
00
000
000
1
T
jii
ij
m
A
α
,
[]
T
T
00
ii
bB =
,
[]
T
T
00
ii
f=Γ
,
[
]
11
iii
CdiagC =
, (2)
the vector x
i
is the state deviations of the i-th area
consisting of 10 components: a
T
, the valve opening
variation of the steam turbine; P
t1
, P
t2
and P
t3
, the
high, intermediate and low pressure output
variations of steam turbine, respectively; a
H
, the gate
opening variation of hydro turbine; v
H
, dashpot
position variation; q, water flow variation of the
hydro-turbine; f, frequency variation; v
i
, the
deviation of the integral area control error (ACE)
(Calovic, 1972; Malik and Hope, 1984/1985); P
ei
,
the deviation of the tie-line power exchange
variations between the i-th and other areas; while u
i
is the deviation of the scalar area control input and ξ
i
is immeasurable variation of the area load; y
i
= [P
T
,
P
H
, f, v, P
e
]
i
T
defined as a vector of the local output
deviations, where P
T
is the output variation of the
steam turbine and P
H
is the one of the hydro unit; η
i
represents the measurement noise vector
corresponding to y
i
. The parameters and matrices,
such as A
ii
, b
i
, C
ii
, f
i
, a
ti
, d
i
, m
ij
and m
ji
, are constant
and with proper dimensions.
It is obvious that the system (1) constructed by N
interconnected subsystems has the multi-overlapping
interconnections represented by the tie line power
deviations, appearing at the last equation of the state
description:
)(
,1
1 jj
T
jiii
N
ijj
T
ijiei
xmxmP −=
∑
≠=
α
&
,
i = 1, 2,......, N, (3)
where, α
1i
= P
10
/ P
i0
is a steady load normalization
factor based on area 1, that is α
11
= 1. The first item
of the sum in (3) is related to the block-diagonal
matrix A
i
, representing N-1 times overlapping
interconnection of state x
ii
(a part of x
i
); while the
coefficients of the second item is spread around the
non-block-diagonal matrix A
ij
, j=1,2,...,N, j
≠
i,
representing the interconnections between the i-th
and the j-th area. Because of power mutual
exchanges, the gross tie line power change
deviations in each area have the following relation
as:
∑
=
=
N
i
iei
P
1
1
0/
α
. (4)
Decompose the system (1) as a group of pair-wise
subsystems (Chen et al., 2002), i.e. only consider the
i-th subsystem state space model coherent with the j-
th subsystem; therefore, the N(N-1)/2 pair
subsystems can be represented by
⎩
⎨
⎧
iiii
jijiiiiiii
xCy
xAuBxAx
η
ξ
+=
+Γ+
+
=
&
(5)
Where
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
00
10
0
1
T
iji
T
i
tiii
i
m
d
aA
A
α
,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
00
000
000
1
T
jii
ij
m
A
α
,
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
258

i = 1, 2, ... , N-1,
j = i+1, i+2,..., N (6)
and the other matrices as in (2). Since the tie line
power equations between the i-th and the j-th
subsystems are of linearly dependent according to
(4), the overlapping interconnected power subsystem
S
ij
in pairs can be rewritten by
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
jj
j
ei
i
ii
jjitjj
T
jij
T
jii
T
iji
T
i
tiii
jj
j
ei
i
ii
x
v
P
v
x
Aa
d
mm
d
aA
x
v
P
v
x
0/00
0/00
000
0010
000
11
11
11
αα
αα
αα
&
&
&
&
&
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
j
i
j
i
j
i
j
i
f
f
u
u
b
b
ξ
ξ
0
00
00
00
0
0
00
00
00
0
,
0000
01000
00100
00010
0000
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
jj
vj
ei
vi
ii
jj
j
ei
i
ii
jj
ii
jj
vj
ei
vi
ii
x
v
P
v
x
C
C
y
y
y
y
y
η
η
η
η
η
i=1, 2, ... , N-1,
j = i+1, i+2,..., N. (7)
where, dotted lines show the two area models with a
overlapping interconnected part. Thus, the power
system, decomposed from a multi-overlapping
interconnected structure to a group of pair-wise
subsystems (Chen et al., 2002), preserves inherent
interconnected features.
3 INCLUSION OF ESTIMATORS
The centralized design of AGC is typically faced
with both conceptual and computational difficulties,
since the necessary information for control has to be
acquired from power areas and generating plants
spread over large geographic territories. It has been
found that the inclusion principle is a suitable tool
for coping with the problem of decentralized AGC
design. However, the problem has been treated
almost exclusively within the framework of
deterministic models and static state or output
feedback (Siljak, 1991). In this section, we shall
present the inclusion of state estimators for a pair of
subsystem S
ij
, based on the stochastic system
inclusion principle.
For a decentralized state estimation of power
systems, the system (1) can first be decomposed as a
pairs of subsystems (5) or (7). Then, in the case of
(7), consider corresponding estimators E
ij
for S
ij
, in
the Kalman filter form:
E
ij
: . (8)
]
ˆ
[
ˆˆ
xCyLBuxAx −++=
&
Where
is the estimations of state
vector
x
ˆ
[
]
T
TTT
jjjeiiii
of S
xvPvxx =
ij
, L is an estimation
gain matrix, other vectors and matrices are
corresponding to S
ij
. Suppose there is a pair
expansion
)E
~
,S
~
(
ijij
for the pair (S
ij
, E
ij
) in the
framework of the input/state/output inclusion, we
state the following:
Definition 1. The pair
)E
~
,S
~
(
ijij
includes the pair
(S
ij
, E
ij
) if there exist two pairs of full rank matrices
(U, V), satisfying UV = I
19
and full rank matrix R
and S, such that for any given initial state vector
[x
0
T
,
0
]
T
ˆ
x
T
and input u(t) the conditions [
0
T
~
x
ˆ
,
0
T
~
x
]
T
=E
w
{[x
0
T
,
0
]
T
ˆ
x
T
; diag[V,V]}and
)(
~
tu
=E
s
{u(t);R}
imply both [x
T
(t),
)
]
(
ˆ
T
tx
T
=C
w
{[
)(
~
T
tx
,
)(
ˆ
~
T
tx
]
T
; diag[U,U]}
and y(t)=C
w
{
)(
~
ty
;S} (
0
tt ≥
∀
t), where E
s
{ּ} and
E
w
{ּ} means strict and weak expansions and C
w
{ּ}
represents weak contraction (see reference Stankovic
et al., 1999).
Theorem 2. The system
ij
S
~
includes the system
S
ij
, in the sense of Definition 1 if and only if
A
i
=
VAU
i
~
,
A
i
B=
RBAU
i
~
~
,
CA
i
=S
i
AC
~
~
V,
A
i
B=S
BAC
i
~
~
~
R,
VГR
ξ
Г
T
V
T
= ,
T
~
~~
ΓΓ
ξ
R
R
η
=S S
η
~
R
T
,
i = 0, 1, 2, .... (9)
There are two special cases of inclusions, i.e.
restriction and aggregation.
Theorem 3. The estimator E
ij
is a restriction of
the estimator
if the system S
ij
E
~
ij
is a restriction of
the system
ij
S
~
and
DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS
259

(VLC =
VCL
~
~
)∩(VLR
η
L
T
V
T
=
T
~
~
~
LRL
η
),
together with one of the followings:
(a)
(VB=
R
B
~
)∩ (VL=
T
L
~
),
(b)
(VBQ=
B
~
)∩(VL=
T
L
~
),
(c)
(VB=
R
B
~
)∩ (VLS= ),
L
~
(d)
(VBQ=
B
~
)∩(VLS=
L
~
),
where Q and T are full rank matrices.
Theorem 4. The estimator E
ij
is an aggregation
of the estimator
ij
E
~
if the system S
ij
is an
aggregation of the system
ij
S
~
and
(LCU =
CLU
~
~
)∩(LR
η
L
T
= ),
TT
~
~~
ULRLU
η
together with one of the followings:
(a)
(BQ=
BU
~
)∩ (LS=
LU
~
),
(b)
(B=
RBU
~
)∩(LS=
LU
~
),
(c)
(BQ=
BU
~
)∩ (L=
TLU
~
),
(d)
(B=
RBU
~
)∩(L=
TLU
~
),
where Q and T are full rank matrices.
4 DECENTRALIZED
ESTIMATION FOR AGC
4.1 Overlapping Decentralized
Estimation
The problem of overlapping structures in the pairs of
subsystems should be solved, i.e. the deviation of the
tie-line power variation of subsystems P
ei
is
decoupled for each subsystem. The algorithm to
expand a pair of subsystem S
ij
and to get
corresponding estimators E
ij
is that, by imposing the
conditions of inclusion principle presented in the
above, a group of expanding matrices can properly
be chosen, aimed at decomposition of overlapping
part represented by dotted lines in (7), such as:
V=block-diag[I
9
, (1 1)
T
, I
9
],
T=block-diag[I
4
, (1 1)
T
, I
4
],
U= block-diag{I
9
, [
β
(1-
β
)], I
9
},
S= block-diag{I
4
, [
β
(1-
β
)], I
4
}, (10)
where, β is a scalar satisfying 0<β<1; the appropriate
complementary matrices M
A
, M
B
,
M
C
and M
L
correspond to the matrices in (7), (8) and satisfy the
equations
A
MVAUA +=
~
,
B
MVBB +=
~
,
C
MTCUC +=
~
,
L
MVLSL +=
~
, (11)
such that
A
~
,
B
~
,
C
~
and
L
~
include the corresponding
matrices of a pair of subsystems and their
estimations, respectively. Although the system S
ij
can become (5) after expanded and modified by
using (10) and (11), it is important to know that the
transform matrices (10) are needed for contractions
to original spaces of each pair subsystems to show
their interconnected relations when the decentralized
estimations and controls are designed.
To formulate overlapping decentralized state
estimation in the framework of LQG control for the
pair subsystems in (7), the non-block diagonal
matrices, such as, A
ij
, j = 1,2,...,N, j i, as
byproducts to be considered after local estimation
and control is established, are neglected. The local
estimation are given by
≠
,
]
ˆ
[
ˆˆ
kkkkkkkkk
xCyLuBxAx −++=
&
k = i, j, (12)
where,
k
denotes the state estimate vector.
Constructing the estimate gain matrices in the block
diagonal form for the pair of decoupled subsystems
as
x
ˆ
],[
~
jiD
LLdiagL =
, (13)
and in order to satisfy the estimator restriction and
aggregation conditions for contractions, we modify
the estimator gain matrix from
D
L
~
to
M
L
~
by adding
L
~
∆
relative to A
ij
, j = 1,2,...,N, j i, to the equation
(13) and obtain
≠
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−+
=
××
×××××
×××
××
jj
jjji
m
i
j
m
ii
ii
M
LL
LLLLLL
LLLL
LL
L
4919
4111111141
411141
1949
00
00
~
. (14)
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
260

Overlapping decentralized state estimator L
S
can be
implemented in the pair subsystems S
ij
by L
S
=
M
TLU
~
directly, or by L
S
S =
M
LU
~
, VL
S
=
M
TL
~
indirectly, based on the Theorem 3 and Theorem 4.
4.2 Fully Decentralized Estimation
Although the estimators described above have been
designed in a decentralized way, they are, essentially,
centralized. The desired features for an efficient
decentralized AGC require that each decentralized
dynamic controller and/or estimator should be
applied to its subsystem, using the measurements
only accessible to its own area (Calovic, 1972 and
1984). In order to comply with these requirements, a
modification of the overlapping decentralized
methodology has been done, leading to a fully
decentralized estimator.
The tie-line power variations depend, essentially,
on the states in both the i-th and the j-th areas.
According to (3) and (8), fully decentralized
estimators can be designed, starting from the
estimator of tie-line power variations defined by
)
ˆ
(
ˆ
eeme
PPLP −=
&
(15)
where, L
m
is an properly chosen constant, adapted to
both dynamics of the tie-line power variations and
the measurement noise. It is obvious that this
estimator is completely autonomous, independent of
the remaining parts of the state vector, having in
mind that the estimators for the remaining parts of
the local state vectors become completely decoupled.
The estimator gain matrix is now modified from (14)
to
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
=
××
××
××
jj
jj
m
m
ii
M
LL
LLL
L
LL
L
4919
1111
1949
00
00
000
00
~
. (16)
As far as the types of expansion are concerned, fully
decentralized estimator schemes are designed in
parallel with the overlapping decentralized ones.
5 EXPERIMENTAL RESULTS
The efficiency of the described estimation schemes
applied to AGC has been tested by simulation. All
the experiments have been done in the case that the
estimators have been implemented together with the
corresponding gain matrices mapping the state
estimates to the control signals. These gain matrices
have been obtained by using the methodology
(Stankovic et al., 1999), based on expansion,
decomposition to subsystems and the local
application of the LQG optimal design. In order to
get a better practical feeling about the quality of
different estimators, responses to a step load
disturbance in area i have been analyzed.
For the pair of subsystems S
ij
, without losing
generality, assume i = 1, j = 2, let the parameters of
the system matrices in (7) correspond to the
references (Chen, 1994; Calovic, 1984; Stankovic et
al., 1999), and have expanding matrices be (10).
Consider the non-balance case of area 1 and area 2,
that is a steady load normalization factor α
12
= P
10
/
P
20
=10. Therefore, choose β = 0.1 and step
disturbance is 0.01 with 5% white noises in ξ
1
.
When y
i
= [P
T
, P
H
, f, v, P
e
]
i
T
, i = 1, 2, the estimators
are designed for full measurement sets; while y
i
= [f,
v, P
e
]
i
T
, i=1,2, the estimators for reduced
measurement sets. The following notation has been
adopted for estimator designs: (1) Overlapping
decentralized (OD) scheme, full measurement sets
(FMS); (2) OD scheme, reduced measurement sets
(RMS); (3) Fully decentralized (FD) scheme, FMS;
(4) FD scheme, RMS. In the case of OD scheme,
L
m
=0; and L
m
=120 for FD.
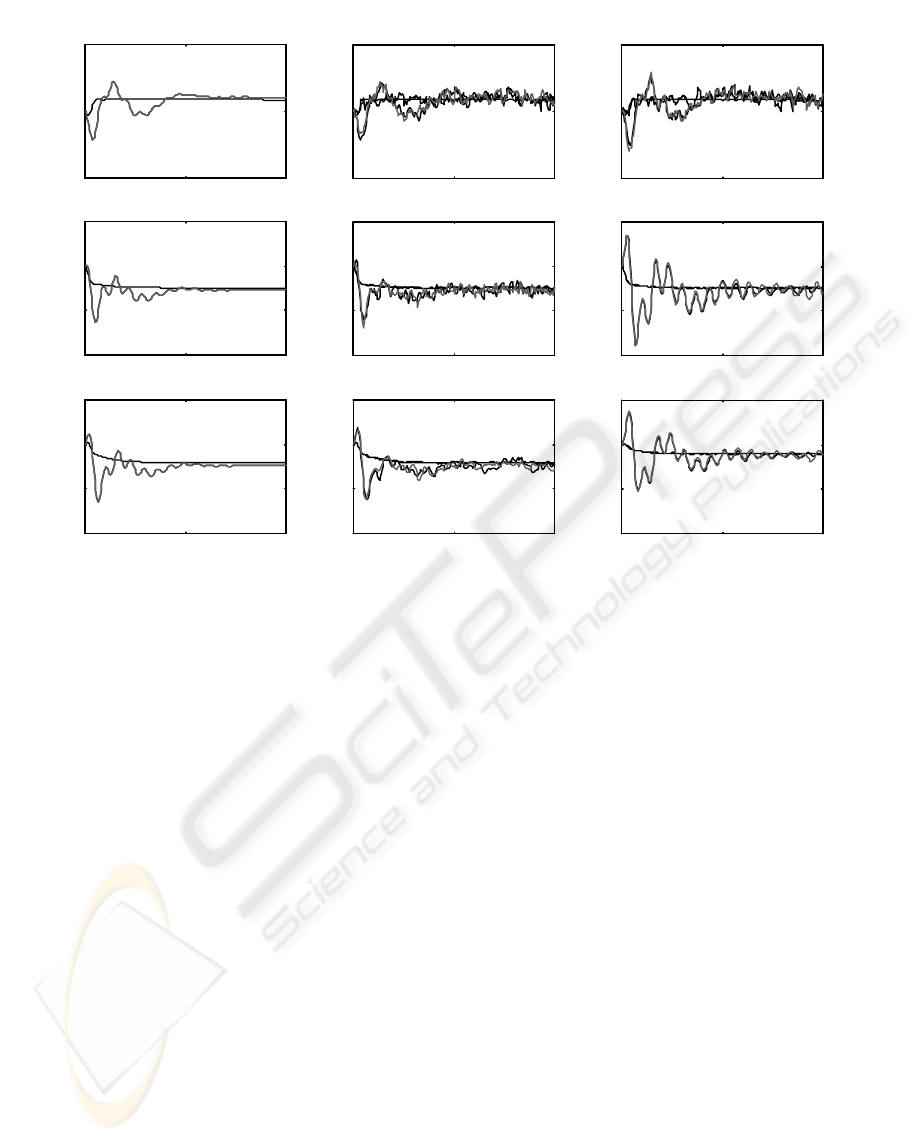
In Figure 1 (a), differences between the globally
optimal estimation errors (obtained by implementing
the globally optimal LQG regulator for the entire
model (7)) and the estimation errors obtained by the
proposed estimators are depicted for f
1
, P
e
and f
2
, all
the noise terms are set to zero, in order to provide a
better insight into the corresponding dynamics.
Smooth overlapped curves are for the cases of 1 and
2, whereas fluctuant overlapped ones for 3 and 4.
Obviously, FD schemes are only slightly inferior to
OD schemes; the number of measurements does not
influence the estimation accuracy significantly.
Figure 1 (b) corresponding to the general situation,
when the stochastic effects are present. It is
interesting to observe that the estimator
decentralization does not degrade the noise
immunity significantly; however, the reduction of
the number of measurements leads in both OD and
FD cases to a visible increase of the estimation error.
This estimator parameter L
m
plays an important role
in achieving the desired overall system performance.
Figure 1 (c) shows the estimation error differences
when L
m
= 20 for FD schemes, corresponding to
Figure 1 (b). Obviously, the estimation quality is
deteriorated.
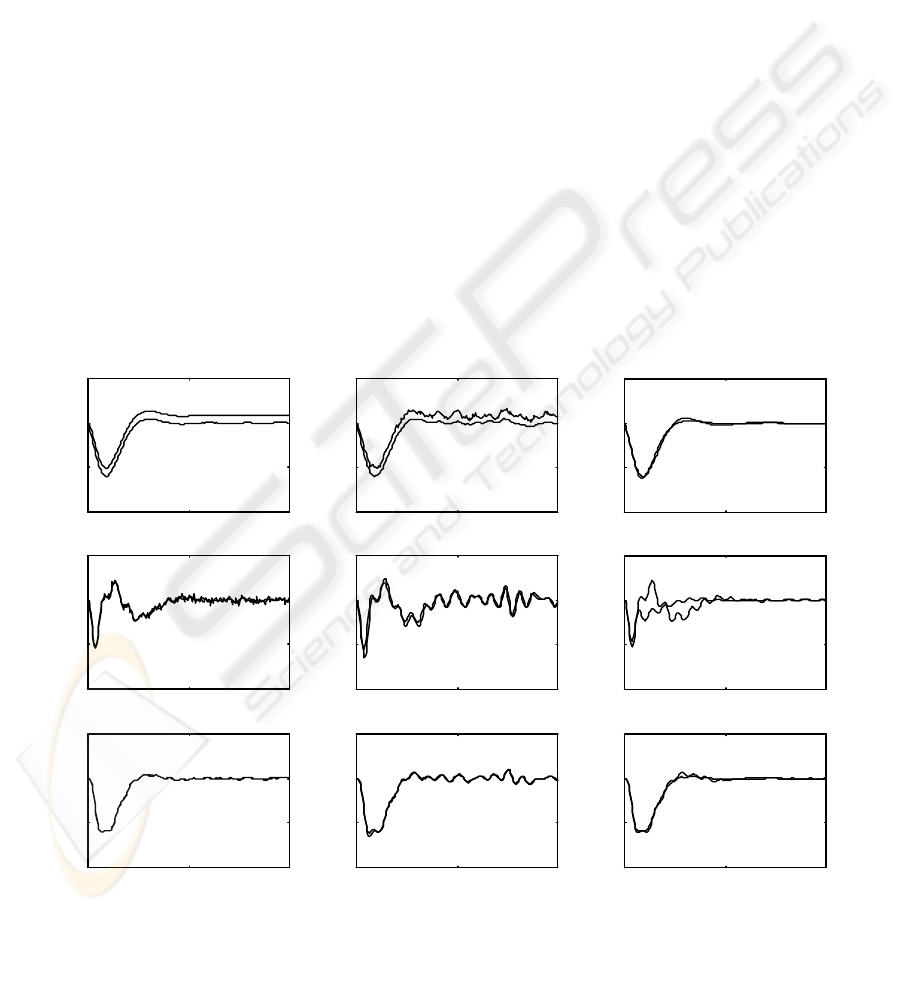
In Figure 2 (a) and Figure 2 (b), the true states
are represented, together with their estimates, for
OD scheme / FMS case and FD scheme / RMS case.
The estimation accuracy is obvious; the bias,
especially pronounced in f
1
, represents a
DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS
261
consequence of the step disturbance, and cannot be
eliminated, since it is viewed as a structural change,
which does not affect the steady-state control error
as the integral action is incorporated into the system
model. The estimates P
e
appear to be very good,
although they are obtained by simple low-pass
filtering. In order to illustrate the performance of the
overall dynamic AGC controllers incorporating the
proposed estimators, The Figure 2 (c) contains the
responses to the step disturbance obtained by the
globally LQG optimal regulator and FD scheme /
FMS case with L
m
= 120.
6 CONCLUSION
In this paper a decentralized state estimator design
methodology is proposed for AGC of the
overlapping interconnected power system.
Overlapping and fully decentralized estimations for
the system is considered from the point of view of
obtaining possibilities for direct contraction from the
expanded to the original space. The design of the
local estimators is based only on the models of the
corresponding areas and the associated tie lines. The
presented experimental results show a very low
performance degradation caused by decentralization.
0
10
20
-5
0
5
x 10
-5
f1/p.u.
0
10
20
-2
-1
0
1
x 10
-3
pe/p.u.
0
10
20
-4
-2
0
2
x 10
-4
f2/p.u.
t/s.
0
10
20
-5
0
5
x 10
-5
f1/p.u.
0
10
20
-2
-1
0
1
x 10
-3
pe/p.u.
0
10
20
-2
-1
0
1
x 10
-4
f2/p.u.
t/s.
0
10
20
-5
0
5
x 10
-5
f1/p.u.
0
10
20
-2
-1
0
1
x 10
-3
pe/p.u.
0
10
20
-2
-1
0
1
x 10
-4
f2/p.u.
t/s.
(a) (b) (c)
Figure 1: Differences of estimation errors.
ACKNOWLEDGEMENT
This research is supported by the NSFC of China under
grant No. 60074002, and by the USRP of Liaoning
Education Department of China under grant No.
202192057.
REFERENCES
Calovic, M. S., 1972. Linear Regulator Design for A Load
and Frequency Control. IEEE Trans. Power. App. Sys.,
Vol. PAS-9, 2271-2285.
Calovic, M. S., 1984. Automatic Generation Control:
Decentralized Area-Wise Optimal Solution. Electric
Power Systems Research, Vol. 7, 115-139.
Chen, X. -B., 1994. Some Aspects of Control Systems
Design Based on The Inclusion Principle. Ph. D.
dissertation, Univ. of Belgrade.
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
262
Chen, X. -B., Stankovic, S. S., 1996. Overlapping
Decomposition and Decentralized LQG Control for
Interconnected Power Systems. Proc. IEEE SMC’96,
Vol.3. 1904-1909.
Chen, X. -B., Siljak, D. D., Stankovic, S. S., 2002.
Decentralized H
∞
Design of Automatic Generation
Control. Proc. of IFAC 15th World Congress.
Barcelona, Spain, July 21-26, 307-312.
Hodzic, M., Siljak, D.D., 1986. Decentralized Estimation
and Control With Overlapping Information Sets. IEEE
Trans. Aut. Control, Vol. AC-31, 81-86.
lftar, A., 1993. Overlapping Decentralized Dynamic
Optimal Control. Int. J. Contr., Vol. 58, 187-209.
Ikeda, M., Siljak, D. D., 1986. Overlapping Decentralized
Control with Input, State and Output Inclusion. Control
Theory and Advanced Technology, Vol. 2, 155-172.
Ikeda, M., Siljak, D. D., White, D. E., 1981. Decentralized
Control with Overlapping Information Sets. J. Optirniz.
Theory and Appl, Vol. 34, 279-310.
Malik, O. P., Hope, G. S., 1984/1985. Decentralized
Suboptimal Load-Frequency Control of A Hydro-
Thermal Power System Using the State Variable
Model. Electric Power systems Research, Vol. 8, 237-
247.
Ohtsuka, K., Morioka, Y., 1997. A Decentralized Control
System for Stabilizing a Longitudinal Power System
Using Tie-Line Power Flow Measurements. IEEE
Trans. on Power Systems, Vol.12, 1202-1209.
Park Y. M., Lee, K. Y., 1984. Optimal Decentralized Load
Frequency Control. Electric Power systems Research,
Vol. 7, 279-288.
Siljak, D. D., 1978. Large-scale Dynamic Systems:
Stability and Structure. North-Holland, NY.
Siljak, D. D., 1991. Decentralized Control of Complex
Systems. Academic Press, New York.
Stankovic, S. S., Chen, X. -B., Matausek, M. R., Siljak, D.
D., 1999. Stochastic Inclusion Principle Applied To
Decentralized Automatic Generation Control. Int. J.
Contr. Vol. 72, 276-288.
0
10
20
-2
-1
0
1
x 10
-3
f1/p.u.
0
10
20
-4
-2
0
2
x 10
-3
pe/p.u.
0
10
20
-2
-1
0
1
x 10
-3
f2/p.u.
t/s.
0
10
20
-2
-1
0
1
x 10
-3
f1/p.u.
0
10
20
-4
-2
0
2
x 10
-3
pe/p.u.
0
10
20
-2
-1
0
1
x 10
-3
f2/p.u.
t/s.
0
10
20
-2
-1
0
1
x 10
-3
f1/p.u.
0
10
20
-4
-2
0
2
x 10
-3
pe/p.u.
0
10
20
-2
-1
0
1
x 10
-3
f2/p.u.
t/s.
(a) (b) (c)
Figure 2: Estimations and responses.
DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS
263
