AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-

SPECIFIED TELECOMMUNICATION SYSTEM

Lyudmila Matvyeyeva

Institute of Cybernetics, NAS of Ukraine, Pr. Glushkowa, 40, Kiev-03187, Ukraine

Sergiy Kryvyy

Institute of Cybernetics, NAS of Ukraine, Pr. Glushkowa, 40, Kiev-03187, Ukraine

Mariya Lopatina

Institute of Cybernetics, NAS of Ukraine, Pr. Glushkowa, 40, Kiev-03187, Ukraine

Keywords: Formal methods

, Petri nets, Linear algebra, MSC, Telecommunication system, verification

Abstract: Last 20 years formal methods are being used widely to specify formally, analyze, verify and test software

and hardware systems, particularly, telecommunication protocols. The paper presents automated verification

system based on Petri nets formal modelling technique and linear algebra methods for automatic proving

structural and some dynamic properties. Application of the system is considered on the telecom example.

1 INTRODUCTION

The Formal Methods are a set of methods and tools

based on mathematical modeling and formal logic

that are used to specify and verify requirements and

architecture of hardware or software systems.

Growing complexity of software and hardware

systems intensify popularity of the formal methods,

which supplement inductive methods, such as

testing, increasing product quality to the level

usually not reachable with the help of testing only

(Miller, 1995). In this respect it is very important to

automate processes of formal specification and

verification to the maximum. The development-

engineers and testers (verifiers) utilize different

language means in their work that usually leads to

the different interpretation of the same functionality,

to uncertainty, and even to inconsistencies or

incompleteness of the requirements. The way out of

this situation is the development of automatic

interfaces between languages of development-

engineers and testers.

2 VERIFICATION SYSTEM

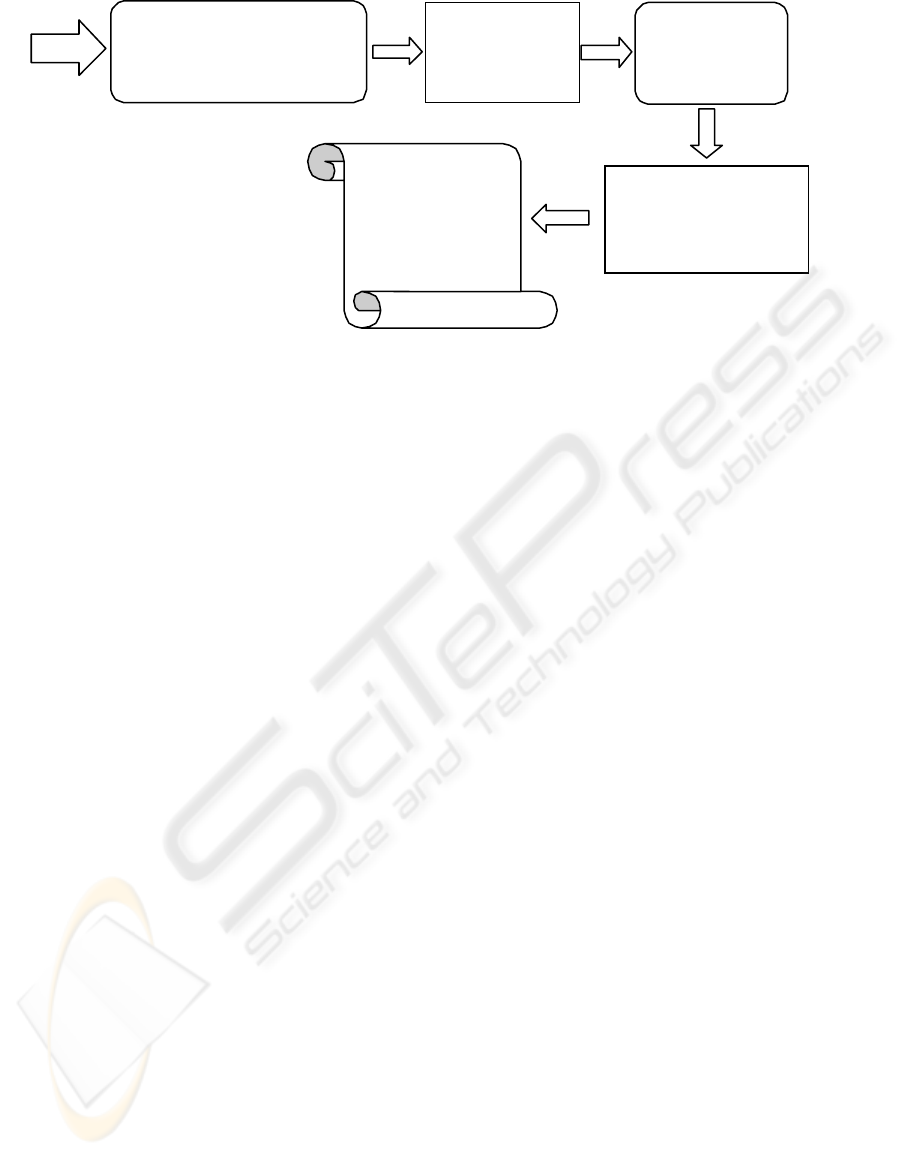
Let’s consider the automated verification system

(see Figure 1) developed to analyse software or

hardware systems specified in MSC language (ITU-

TS, 2000). The system conforms to the following

requirements: verification process is fully automatic;

the language of the output verdict is MSC as well.

As a formal model the system utilizes ordinary

Petri net (PN) because of their profound support for

analysis of many properties and problems associated

with concurrent systems – the most difficult in

manual testing.

Given work uses the algorithm of translation

MSC diagrams into Petri net (PN) developed by the

authors of this paper. The algorithm works over

selected subset of basic MSC elements. The

description of the translation algorithm with the

proof, and the example are presented in (Kryvyy,

2003). The proof of the algorithm correctness is

based on the use of process algebra ACP (Bergstra,

1984). We would like to underline here that the most

significant feature of the given algorithm is the way

of handling of MSC’s conditions, since the literature

402

Matvyeyeva L., Kryvyy S. and Lopatina M. (2004).

AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-SPECIFIED TELECOMMUNICATION SYSTEM.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics , pages 402-405

DOI: 10.5220/0001138804020405

 SciTePress

indicates this problem in the translation process as

the most difficult (Mauw, 1995).

Resulted PN is analysed automatically to verify

the properties of the system using linear algebra.

Systems of linear equations over the set of natural

numbers are resolved using TSS method (Kryvyy,

2002) developed by one of the authors of this paper,

and which shows very high performance on large-

scale systems comparatively to the existing methods.

Given work is based on well-known definitions

of PNs theory, and classical definitions of Incidence

Matrix, State Equation and PN Invariants (Murata,

1989).

3 TELECOM EXAMPLE

Let’s consider the example of translation and

analysis of the real telephone system with basic

services traditionally called Plain Old Telephony

Service, POTS. The formal model of POTS is

presented as ordinary PN. One of the advantages of

building a formal model is to ensure the design is

correct and meets certain requirements. A correct

design of POTS at least has the following required

properties: must be a limitation on connection

channels resource usage; the telephone network

restores to its initial state after a talk of two

subscribers; the subscribers can call each other

indefinite number of times irrespectively given

network configuration; the telephone network can’t

get in deadlock state.

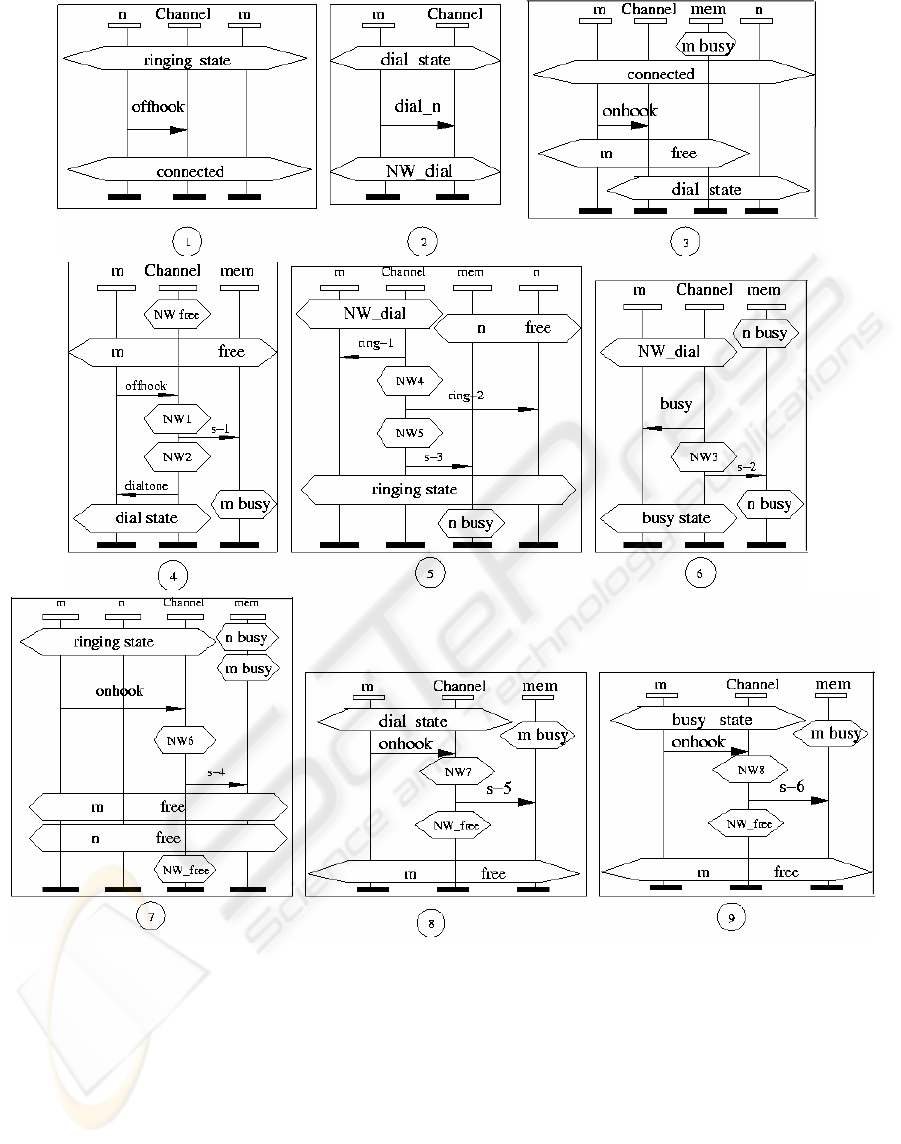
The set of MSC-diagrams presented in the

Figure 2 describes the work of POTS. Note that

MSC-diagrams Nº3, 4 and 8 on the Figure 2 shall be

repeated symmetrically relative to m

instances.

) instance corresponds to m

) subscriber.

Let’s apply to the given set of MSCs the

algorithm of automatic translation (refer to section

2), and simplify obtained PN using net reduction

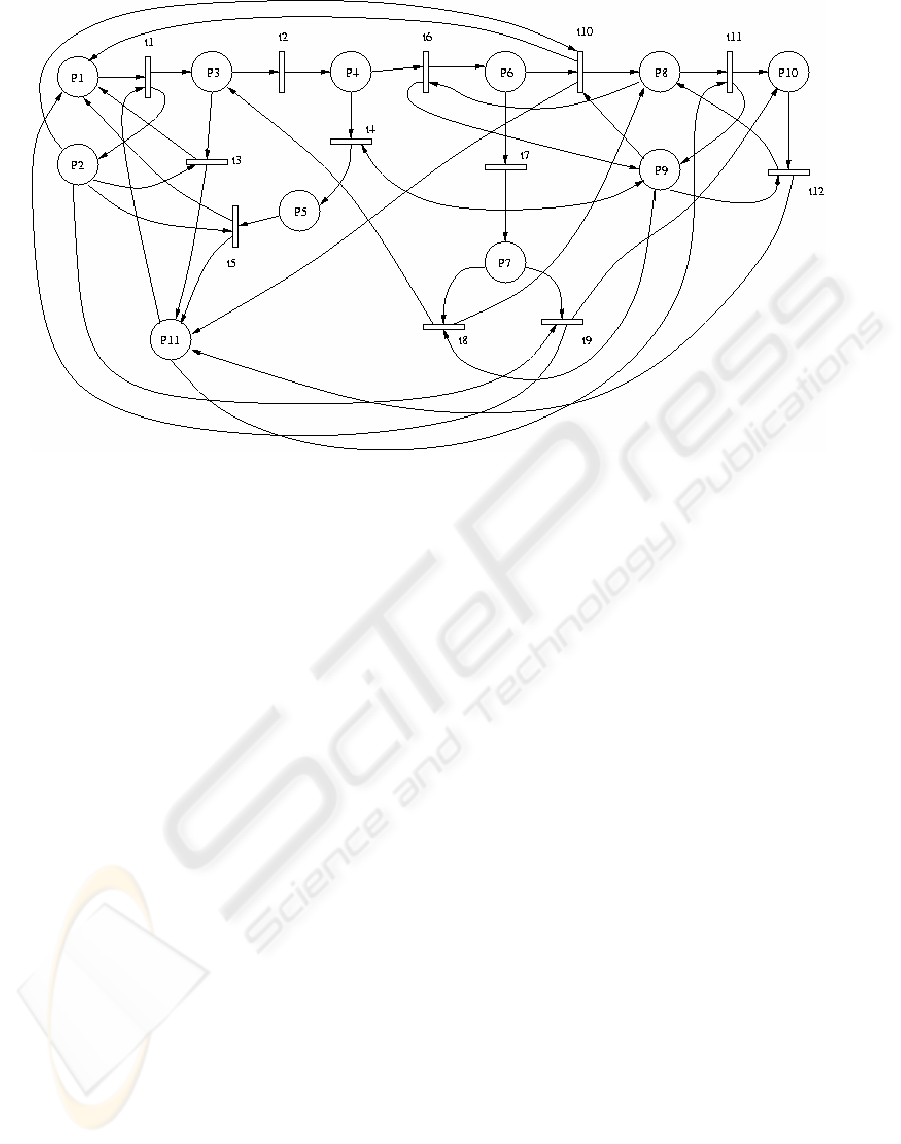
(Murata, 1989). The resulting ordinary PN is

illustrated in the Figure 3. The initial PN marking is

=(1,0,0,0,0,0,0,1,0,0,k), where k is the number of

connection channels. The 11-th place models pair

connections of the all network subscribers, and

corresponds to connection channels resource. So, we

have built the formal model aimed at analysis and

verification of the real system. In the given PN,

transitions are respectively interpreted as events of

data message transitions in the MSCs (Figure 2) in

the following way: t1=offhook(m), t2=dial_n,

t3=onhook(m), t4=busy, t5=onhook(m),

t6=ring(m,n), t7=offhook(n), t8=onhook(n),

t9=onhook(m), t10=onhook(m), t11=offhook(n),

t12=onhook(n); where offhook(m) means that the

subscriber hang off the phone,

onhook(n)/onhook(m) means that the n

subscriber hang on the phone, ring(m,n) means that

is calling n

. The PN’s places in the Figure 3 are

named respectively as conditions of the given

MSCs: P1=“m free”, P2=“m busy”, P3=”dial state”,

P4=”NW_dial”, P5=”busy state”, P6=”ringing

state”, P7=”connected”, P8 =”n free”, P9=”n busy”,

P10=”dial state”, P11=”NW_free”.

To verify the correctness of the given model for

POTS with respect to the above properties it’s

necessary to calculate the PN’s S- and T-invariants.

The following invariants of the PN are obtained

automatically using TSS method (Kryvyy, 2002):

S-invariants — s

=(0,1,1,0,0,0,0,0,0,0,0),

=(0,0,0,0,0,1,0,1,0,0,0), s

=(1,0,0,1,1,1,1,0,0,0,0),

=(0,1,0,1,1,0,1,0,1,1,0), s

=(1,0,1,0,0,0,0,0,0,0,1,),

=(0,0,0,0,0,0,0,1,1,1,1), s

=(1,0,0,1,1,0,1,0,1,1,1);

T-invariants — t

=(1,0,1,0,0,0,0,0,0,0,0,0),

=(0,0,0,0,0,0,0,0,0,0,1,1), t

=(1,1,0,1,1,0,0,0,0,0,0,0),

=(1,1,0,0,0,1,0,0,0,1,0,0), t

=(0,1,0,0,0,1,1,1,0,0,0,0),

=(1,1,0,0,0,1,1,0,1,0,0,1).

Automatic analysis of invariants of the PN

proves the following properties of this model.

Boundedness: The given PN is structurally

A u tom a tic

tran slationofMSCs

intoPetriNet

Automaticanalysisof

th eformalmodel



PetriNetwhi c h

representtheformal

modelofthesy ste m





Theset ofMSCs

whi chdesc ribes

th esy st em



Ve rdictofthe

sy stem’sanalysis

(e rr orsan d 

problemsofthe

sy stemrepresented

in MSC la ng uag e )

ure1

Figure 1

AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-SPECIFIED TELECOMMUNICATION SYSTEM

403

bounded. Indeed, all PN’s places are covered by

non-zero coordinates from the set of S-invariants.

Physical interpretation of this property means that

there is a limitation on resource usage.

Repetitiveness, Consistency, and L3-liveness.

Since there exist a live initial marking 

for this

PN, and all transitions are covered by non-zero

coordinates from the set of T-invariants the PN is

repetitive, and L3-live

. Physical interpretation of this

properties means that POTS will never be

deadlocked and any connection of two subscribers

can be performed as many times as needed. The PN

is consistent because any marking M is reachable

from itself. This means that the system always

returns into its initial state.

So far, conducted analysis shows that the formal

model has the required properties of the real system

and the given set of MSC diagrams correctly

describes POTS model.

The reference table, which is built during the

translation in order to preserve the correspondence

between system’s descriptions in MSC language and

Figure 2: MSC

- diagrams representing all possible POTS protocols

ICINCO 2004 - ROBOTICS AND AUTOMATION

404

Petri net representation, allows to present detected

problems and errors in MSC diagrams format in

output verdict.

4 CONCLUSION

To conclude, let’s underline, that the main properties

of the developed technological process are the

following: firstly, the process is completely

automated, and, secondly, the input language and the

language of output verdict represent the operating

language of the development-engineers, namely,

MSC, and so far do not require specific

mathematical background.

The further investigation will be directed at

extension to the whole MSC language and building

automated translators from SDL, UML and other

languages. The long term goal of this investigation is

building of the unified technological line partially or

fully automated, which will allow in its frames to

design, analyze, verify and test the wide class of the

properties of the systems under development.

REFERENCES

ITU-TS, 2000. Recommendation Z.120: Message

Sequence Chart (MSC). ITU-TS, Geneva.

Miller S.P., Srivas M., 1995. Formal Verification of the

AAMP5 Microprocessor – A Case Study in the

Industrial Use of Formal Methods. In Proceedings of

the 1995 Workshop on Industrial-Strength Formal

Specification Techniques (WIFT’95), IEEE Computer

Society, Orlando, Florida, USA, April 5-8.

Kryvyy S., Matvyeyeva L., Lopatina M., 2003. Automatic

Transformation of MSC Diagrams into Petri Nets. In

Proceedings of SCI’2003, Orlando, USA, 29-31 July,

vol. 5, pp. 140-146

Kryvyy S. , 2002. A Criteria of compatibility systems of

linear diophantine constraints. LNCS 2328, Springer

Verlag, pp. 264-271.

Murata T., 1989. Petri Nets: Properties, Analysis and

Applications. In Proceedings of the IEEE, vol.77,  4,

pp. 541-580.

Kluge O., Padberg J., Ehrig H., 2001. Modeling Train

Control Systems: From Message Sequence Charts to

Petri Nets, Technische Universität Berlin. Retrieved

on April 20, 2001 from http://cs.tu-

berlin.de/SPP/index.html.

McMillan K. L., 1992. Using Unfolding to Avoid the State

Explosion Problem in the Verification of

Asynchronous Circuits. In Proc. 4th Workshop on

Computer Aided Verification, LNCS 663, pp. 164-174.

Mauw S., Reniers M.A., 1995. Thoughts on the meaning

of conditions. Experts meeting SG10, St.Petersburg

TD9016, ITU-TS.

Bergstra J.A., Klop J.W., 1984. Process Algebra for

Synchronous Communication, Inf.&Control 60,

pp.109-137.

Figure 3: The PN corresponding to the set of MSC

diagrams in the Figure 2

AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-SPECIFIED TELECOMMUNICATION SYSTEM

405