INVARIANT FEATURES FOR CHARACTER RECOGNITION
Ryszard S. Chora
´
s
Institute of Telecommunications, University of Technology & Agriculture
Kaliskiego Street 7, 85-796 Bydgoszcz, Poland
Keywords:
Feature extraction, character recognition, moment invariants.
Abstract:
This paper presents feature extraction method for recognition of isolated characters. Feature extraction is most
important factor in achieving high recognition performance. We presented moments invariants as features for
pattern recognition. This article analyzes the image feature extraction task on the basis of moments invariants
for image recognition problem.
1 INTRODUCTION
Handwritten recognition have been a main research
subject in pattern recognition for over thirty years.
The application of handwritten character recognition
is broad. Typical uses include recognition of hand-
written zip codes and reading personal bank checks.
The recognition of handwritten characters, like other
problems in pattern recognition, consists of two major
problems: feature selection and pattern classification.
Feature selection is problem-dependent and consid-
ered most significant to the final result of a recog-
nition system. Since handwritten characters of the
same character class can occur in great variety, it is
desirable to generate a representation that is invariant.
A feature-based recognition of objects which is inde-
pendent of their position, size, orientation and other
variations has been the goal of much recent research.
There have been several kinds of features used for
recognition:
visual features (contours, textures),
transform coefficient features,
statistical features (moment invariants).
The objective of this paper is to develop an algo-
rithm for the automatic recognition of handwritten
characters. In the algorithm a binary image of the
character is obtained and its skeleton is then produced
by utilizing a standard thinning algorithm. The clas-
sification process incorporates features of the char-
acters such as number of intersections, number of
free ends, as well as criteria derived from normal-
ized moments. Moment invariants derived by (Hu,
1999),(Flusser, 1993) are invariant only under trans-
lation, rotation and scaling of the object. In this paper
we use features which are also invariant under gen-
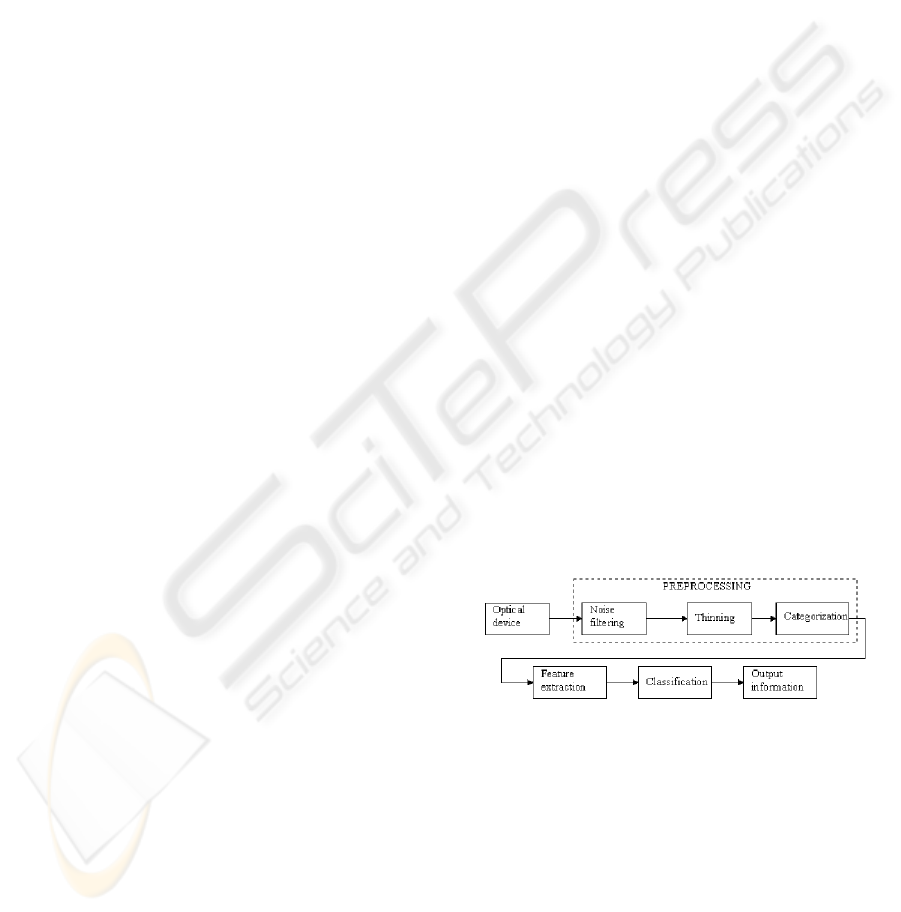
eral affine transformations. The block structure of the
recognition system is given in Figure 1. The prepro-
cessing stage includes noise filtering, thinning, and
character categorization. The feature extraction and
classification are described in the next paragraphs.
Figure 1: Block diagram of the proposed system.
2 PREPROCESSING
A character pattern is fed to a camera system,
and the camera signal is transformed into binary
image. The camera must be perpendicular to the
character plane and contrast between characters and
background must be reasonable. A binary image is
regarded as a set of image points (pixels with value 1).
102
Chora
´
s R. (2004).
INVARIANT FEATURES FOR CHARACTER RECOGNITION.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 102-107
DOI: 10.5220/0001139201020107
Copyright
c
 SciTePress

The pictorial information is represented as a
function of two variables (i, j). The image in its
digital form is usually stored as an two-dimensional
array. If M = {1, 2, . . . , m} and N = {1, 2, . . . , n}
are the spatial domains, then D = M × N is the
set of resolutions cells and the digital image P is
a function which assigns binary value to each and
every resolution cells, i.e. P : M × N −→ B.
Noise pixels add irregularities to the outer bound-
ary of the characters and may have undesired effects
on the recognition system. A smoothing algorithm
eliminates small areas and fills little holes. The algo-
rithm modifies each pixel according to its initial value
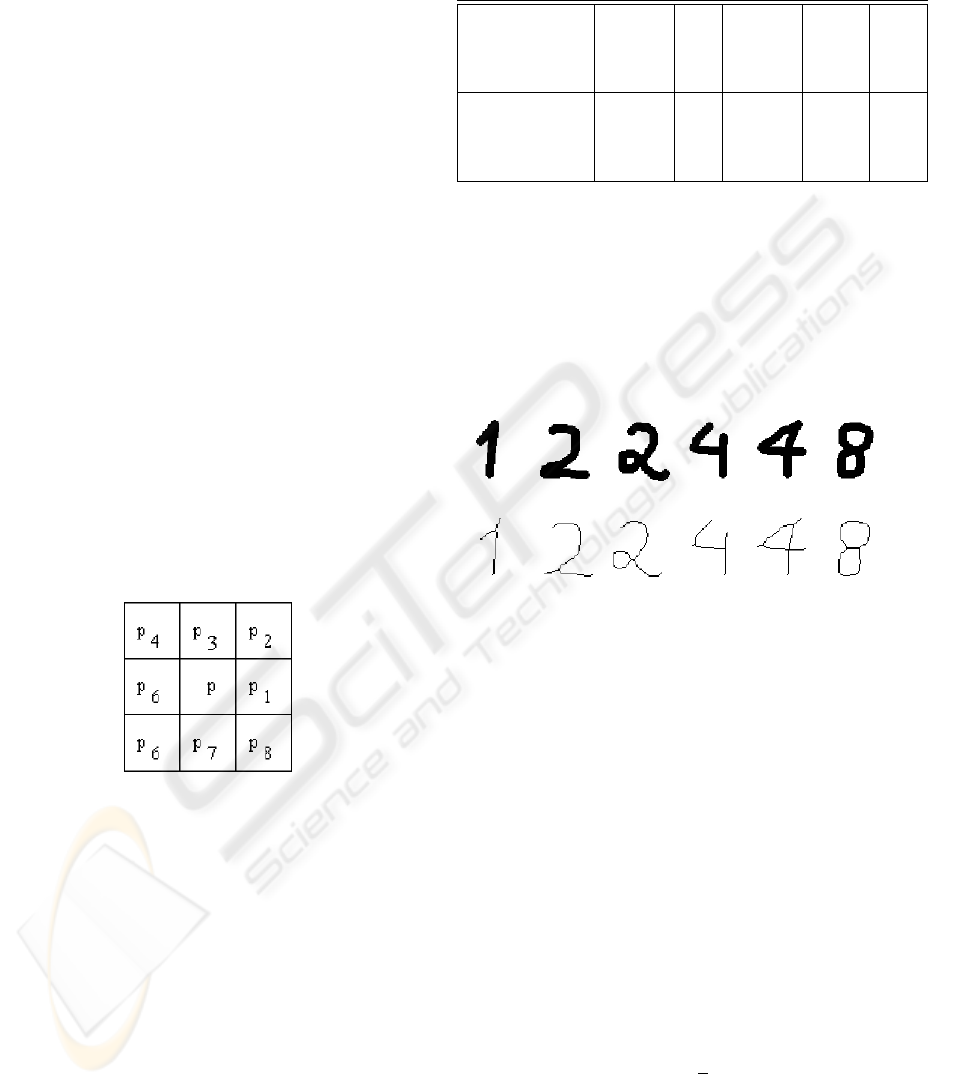
and to those of its neighborhood (Figure 2) according
to the following conditions:
If p = 1 then p
0
=



0 if
8
P
i=1
p
i
≤ T
1
1 otherwise
else p
0
=



1 if
8
P
i=1
p
i
iT
2
0 otherwise
(1)
where p is current pixel value, p
0
the new pixel
value and and T
1
are T
2
the threshold values.
Figure 2: Pixel notation
2.1 Thinning of the characters
A pixel is considered deletable if it satisfies the fol-
lowing conditions:
1. 1 < B(p) ≤ 7 where B(p) =
8
P
i=1
p
i
2. A(p) = 1 is number of 01 transitions in the eight
neighbors of pixel p.
Additional conditions may permit the removal of ele-
ment if it is on south or east edge or if is on a corner
3. (p
1
= 0) or (p
7
= 0) or (p
3
= 0 and p
5
= 0)
Table 1: Topological properties of p
THE VALUE
OF N
4
C
OR
N
8
C
0 1 2 3 4
PROPERTY
OF PIXEL p
Internal
or iso-
late
End Connect Branch Cross
The next conditions may permit the removal of el-
ement if it is on north or west edge or if it is on a
corner
4. (p
3
= 0) or (p
5
= 0) or (p
1
= 0 and p
7
= 0)
Figure 3: Original a) and thinned b) characters
2.2 Character categorization
A particular difficulty encountered in handwritten
characters classification is the large variations in to-
tal properties of patterns. For character categorization
we used information derived from connected number
of point p .When p = 1 , the connected number N
c
of
p is defined by the next equation
N
4
C
=
X
k∈S
(p
k
− p
k
p
k+1
p
k+2
) (2)
N
8
C
=
X
k∈S
(¯p
k
− ¯p
k
¯p
k+1
¯p
k+2
) (3)
where: S = (1, 3, 5, 7) and p means (1 − p).
Topological properties of the pixel p are shown in
Table 1, and the distribution of characters into the
categories is shown in Table 2.
INVARIANT FEATURES FOR CHARACTER RECOGNITION
103

Table 2. Distribution of characters into the categories.
3 MOMENT-BASED CHARACTER
CLASSIFIERS
3.1 Geometric Moments
Any character can be represented by the spatial mo-
ments of its intensity function
m
pq
=
Z Z
F
pq
(i, j)p(i, j)didj (4)
where p(i, j) is the intensity function representing
the image, the integration is over the entire image and
the F (i, j) is the same function of i and j for example
i
p
J
q
, or a sin(ip) and cos(jq). In the spatial case
m
pq
=
m
X
i=1
n
X
j=1
i
p
j
q
p(i, j) (5)
The characteristic function of f (x, y) is defined as
its conjugate Fourier transform and may be expanded
as a power series in u, v , as the following
F (u, v) =
Z Z
e
−i2π(xu+yv)
dxdy =
=
∞
X
p=0
∞
X
q=0
(−i2π)
p+q
p!q!
m
pq
u
p
v
q
(6)
The infinite set of moments
m
pq
, p, q = 0, 1, 2, . . . uniquely determine f(x, y),
and vice-versa
f(x, y) =
X
u
X
v
e
i2π(xu+yv)
[
∞
X
p
∞
X
q
(−i2π)
p+q
p!q!
u
p
v
q
]
(7)
The central moments are given by
m
pq
=
m
X
i=1
n
X
j=1
(i − I)
p
(j − J)
q
p(i, j) (8)
where (I, J) are
I =
m
10
m
00
and J =
m
01
m
00
(9)
Normalized central moment µ
pq
µ
pq
=
m
pq
(m
00
)
α
, α =
p + q
2
+ 1 (10)
Using nonlinear combinations of the lower order
moments, a set of moment invariants (usually called
geometric moments), which has the desirable proper-
ties of being invariant under translation, scaling and
rotation, is derived. Hu (Hu, 1999) employed seven
moment invariants, that are invariant under rotation
as well as translation and scale change, to recognize
characters independently of their position size and
orientation.
φ
1
= µ
20
+ µ
02
φ
2
= [µ
20
− µ
02
]
2
+ 4µ
2
11
φ
3
= [µ
30
− 3µ
02
]
2
+ [3µ
21
− µ
03
]
2
φ
4
= [µ
30
+ µ
12
]
2
+ [µ
21
+ µ
03
]
2
(11)
φ
5
= [µ
30
− 3µ
12
][µ
30
+ µ
12
]×
×[(µ
30
+ µ
12
)
2
− 3(µ
21
+ µ
03
)
2
]+
+[3µ
21
− µ
03
][µ
21
+ µ
03
]×
×[3(µ
30
+ µ
12
)
2
− (µ
21
+ µ
03
)
2
]
φ
6
= [µ
20
− µ
02
][(µ
30
+ µ
12
)
2
− (µ
21
+µ
03
)
2
] + 4µ
11
[µ
30
+ µ
12
][µ
21
+ µ
03
]
φ
7
= [3µ
21
− µ
03
][µ
30
+ µ
12
]×
×[(µ
30
+ µ
12
)
2
− 3(µ
21
+ µ
03
)
2
]
−[µ
03
− 3µ
12
][µ
21
+ µ
03
]×
×[3(µ
30
+ µ
12
)
2
− (µ
21
+ µ
03
)
2
]
Any function of moments which is invariant under
the general affine transformation
i
0
= a
11
i + a
12
j + a
01
j
0
= a
21
i + a
22
j + a
02
(12)
is invariant under simple six transformations
1) j
0
= j i
0
= i + a 2) i
0
= i j
0
= j + b
3) i
0
= wi j
0
= wj
4) j
0
= j i
0
= di 5) j
0
= j i
0
= i + tj
6) i
0
= i j
0
= j + t
0
i
The central moments are invariant under the trans-
lation 1 and 2. Normalized central moments are in-
variant under the scaling 3. We are interested in find-
ing moments invariants also under other transforma-
tions e.g. one-axis scaling 4 and skew transformation
5 and 6. Next combinations will provide compound
moments that support recognition of the characters
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
104

I
1
= µ
20
µ
02
− µ
2
11
I
2
= (µ
30
µ
03
− µ
21
µ
12
)
2
−
4(µ
30
µ
12
− µ
2
21
)(µ
21
µ
03
− µ
2
12
)
I
3
= µ
20
(µ
21
µ
03
− µ
2
12
) − µ
11
(µ
30
µ
03
− µ
21
µ
12
)+
µ
02
(µ
30
µ
12
− µ
2
21
)
I
4
= µ
2
30
µ
3
02
− 6µ
30
µ
21
µ
11
µ
2
02
+
+6µ
30
µ
12
µ
02
(µ
2
11
− µ
20
µ
02
)+
+µ
30
µ
03
(6µ
20
µ
11
µ
02
− 8µ
3
11
)
+9µ
2
21
µ
20
µ
2
02
− 18µ
21
µ
12
µ
20
µ
11
µ
02
+
+6µ
21
µ
03
µ
20
(2µ
2
11
− µ
20
µ
02
) + 9µ
2
12
µ
2
20
µ
02
−6µ
12
µ
03
µ
11
µ
2
20
+ µ
2
03
µ
3
20
I
5
= µ
20
+ µ
02
I
6
= (µ
20
− µ
02
)
2
+ 4µ
2
11
I
7
= (µ
30
− 3µ
12
)
2
+ (µ
03
− 3µ
21
)
2
I
8
= (µ
30
+ µ
12
)
2
+ (µ
03
− µ
21
)
2
(13)
I
9
= (µ
30
− 3µ
12
)(µ
30
+ µ
12
)×
×[(µ
30
+ µ
12
)
2
− 3(µ
03
+ µ
21
)
2
]+
+3(µ
21
− µ
03
)(µ
03
+ µ
21
)×
×[3(µ
30
+ µ
12
)
2
− (µ
03
+ µ
21
)
2
]
I
10
= (µ
20
− µ
02
)[(µ
30
+ µ
12
)
2
− (µ
03
+ µ
21
)
2
]+
+4µ
11
(µ
30
+ µ
12
)(µ
03
+ µ
21
)
I
11
= (3µ
21
− µ
03
)(µ
30
+ µ
12
)×
×[(µ
30
+ µ
12
)
2
− 3(µ
03
+ µ
21
)
2
]+
+(3µ
12
− µ
30
)(µ
03
+ µ
21
)×
×[3(µ
30
+ µ
12
)
2
− (µ
03
+ µ
21
)
2
]
I
12
= µ
40
µ
04
− 4µ
31
µ
13
+ 3µ
2
22
I
13
= µ
40
µ
22
µ
04
− 2µ
31
µ
22
µ
13
−
µ
2
40
µ
13
− µ
04
µ
2
31
− µ
3
22
I
14
=
I
4
µ
00
I
2
I
15
=
I
2
1
µ
00
I
3
I
16
=
I
1
I
3
I
4
The algebraic moment invariants are computed
from the first t central moments and are given as the
eigenvalues of predefined matrices, M[j, k], whose
elements are scaled factors of the central moments.
In contrast to Hu’s geometric moment invariants, the
algebraic moment invariants can be constructed up
to arbitrary order and are invariant to affine transfor-
mations. The algebraic moment transform of (Eqn.
5) can be extended to generalized form by replacing
the conventional transform kernel i
p
j
q
with a more
general kernel of P
p
(i)P
q
(j) - the Legendre polyno-
mial or Zernike polynomial respectively. Since both
Legendre and Zernike polynomials are complete sets
of orthogonal basis, Legendre and Zernike moments
are called orthogonal moments. Orthogonal moments
allow to accurately reconstruct the described shape.
They make optimal utilization of shape information.
3.2 Zernike moments
Zernike moment of order n and repetition m is de-
fined as (Khotanzad, 1990), (Teh, 1988)
Z
nm
=
n + 1
π
ZZ
x
2
+y
2
≤1
V
∗
nm
(ρ, θ)f(x, y)dxdy (14)
where:
- f(x, y) is the image intensity at (x, y) in Cartesian
coordinates,
- V
∗
nm
(ρ, θ) is a complex conjugate of
V
nm
(ρ, θ) = R
nm
(ρ)e
jmθ
in polar coordinates
(ρ, θ),
- n ≥ 0, and n − |m| is even positive integer.
The polar coordinates (ρ, θ) in the image domain
is related to the Cartesian coordinates (x, y) as x =
ρcos(θ) and y = ρsin(θ).
R
nm
(ρ) is a radial defined as (Khotanzad, 1990), as
follows:
R
nm
(ρ) =
n−|m|
2
X
s=0
(−1)
s
[(n − s)!]ρ
n−2s
s!(
n+|m|
2
− s)!(
n−|m|
2
− s)!
(15)
The first six orthogonal radial polynomials are:
R
00
(ρ) = 1 R
11
(ρ) = ρ
R
20
(ρ) = 2ρ
2
− 1 R
22
(ρ) = ρ
2
R
31
(ρ) = 3ρ
3
− 2ρ R
33
(ρ) = ρ
3
(16)
Zernike moments, which are proven to have very
good image feature representation capabilities, are
based on the orthogonal Zernike radial polynomials.
Zernike moments are defined as continuous integrals
over a domain of normalized coordinates. The
implementations of such moment functions therefore
involve the following sources of errors: (i) the dis-
crete approximation of the continuous integrals, and
(ii) the transformation of the image coordinate system
into the domain of the orthogonal polynomials.
Moments of order n with repetition m of a discrete
image function f(k, l) with spatial dimension M ×N
are given by
Z
nm
=
n + 1
π
M−1
X
k=0
N−1
X
l=0
f(k, l)R
nm
(ρ
k,l
)e
−jmθ
kl
(17)
where the discrete polar coordinates
ρ
kl
=
q
x
2
l
+ y
2
k
θ
kl
= arctan(
y
k
x
l
) (18)
are transformed by
INVARIANT FEATURES FOR CHARACTER RECOGNITION
105

Table 2: Hu moments invariants for characters with Figure 3.
Hu moments invariants
1 6.7E-004 3.7E-010 5.6E-015 2.1E-014 1.3E-028 2.5E-019 -1.8E-028
2 6.8E-004 4.9E-010 2.0E-015 7.8E-015 6.0E-030 1.0E-019 3.0E-029
2 6.9E-004 2.2E-010 2.3E-014 1.4E-014 2.4E-028 1.1E-019 -1.1E-028
4 6.8E-004 7.4E-011 8.9E-016 8.2E-015 4.8E-030 -5.7E-020 2.2E-029
4 7.0E-004 3.3E-010 7.8E-015 1.4E-014 -1.4E-028 -1.4E-019 -1.7E-029
8 6.9E-004 2.0E-010 2.2E-015 4.4E-015 6.7E-030 2.9E-020 -1.2E-029
x
l
= c +
l(d − c)
N − 1
y
k
= d −
k(d − c)
M − 1
(19)
for k = 0, . . . , M − 1 and l = 0, . . . , N − 1. c and d
are real numbers take values as shown in Figure 4.
To calculate the Zernike moments of an image
f(x, y) , the image is first mapped to the unit disk
using polar coordinates, where the centre of the
image is the origin of the unit disk. Those pixels
falling outside the unit disk are not used in the
calculation.
Figure 4: Mapping of a discrete image function a)c = −1,
d = 1 and b)c =
−1
√
2
, d =
1
√
2
Normalize the Zernike moments
Z
mn
=
Z
0
nm
m
00
(20)
where, Z
mn
is the Zernike moments.
Because Z
mn
is complex, we often use the Zernike
moments modules |Z
mn
| as the features of shape in
the recognition of pattern.
The magnitude of Zernike moments has rotational
invariant property. An image can be better described
by a small set of its Zernike moments than any other
types of moments such as geometric moments, Leg-
endre moments, rotational moments, and complex
moments in terms of mean-square error. Zernike mo-
ments do not have the properties of translation invari-
ance and scaling invariance. The way to achieve such
invariance is images translation and image normaliza-
tion before calculation of Zernike moments.
4 SIMILARITY MEASURE
Recognition is made by associating a feature vector
calculated for unknown character with a set of feature
vectors for a character obtained with a similar train-
ing set. The moment invariant approach to charac-
ter identification attempts to represent the pattern by
a set of K moments invariant-features, thus as a point
in K-dimensional feature space. Points corresponding
to patterns of the same class are assumed to be close
together, not close to those of different classes. The
similarity distance (d
m
) between two feature vectors
M
X
and M
Y
for a pair of character images X and Y
( C(ategory) code image X is identical to C(ategory)
code image Y ) is computed as the Euclidean distance
as follows
d
m
(M
X
, M
Y
) =
v
u
u
t
K
X
k=1
(m
X
k
− m
Y
k
)
2
(21)
The value of d
m
is zero or small for identical or
similar characters and high for different characters.
5 CONCLUSION
The main contribution of this paper is presentation
of character recognition using set of orthogonal
moments. In particular, we have constructed feature
vector by applying the normalized various moments.
This vector used in conjunction with a simple clas-
sification measure such as the Euclidean distance, is
capable of achieving satisfactory performance levels.
In our experiment we used our own database which
provides handwritten numerals from a hundred writ-
ers. Each numeral has 10 samples. Since the size of a
sample image varies, we first normalized each image
into the size of pixels. If the Hu moments invariants
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
106

were used, the recognition rate of over 93.2% could
be obtained. Five samples of each characters were
used as training sets. The recognition rate of using all
combinations of moments Eq.13 was found to be sig-
nificantly better - 98.7%. For real time applications,
we prefer only first four moment invariants e.g. with
recognition rate 96.8%. When more training sets were
used, the recognition rate was found to be higher.
REFERENCES
Hu, M. (1999). Pattern recognition by moment invariants.
Proc. IRE.vol. 49, pp.1428. .
Flusser, J., Suk, T.(1993) Pattern recognition by affine mo-
ment invariants. Pattern Recognition, vol. 26, pp. 167-
174.
Haralick, R., Shanmugam, K., Dinstein, I. (1973) Textural
features for image classification. IEEE Trans. on Sys-
tems, Man, and Cybernetics. SMC-3(6), pp.610-621,
1973.
Iivarinen, I., Peura, M., Sarela, J., Visa, A. (1997) Compar-
ision of combined shape descriptors for irregular ob-
jects. Proc. 8th British Machine Vision Conf.. vol.2,
pp.430-439, 1997.
Suen, C. Y., Nadal, C., Mai, T.A., Legault, R., Lam, L.
(1992) Computer recognition of unconstrained hand-
written numerals. Proc. IEEE, vol. 80 (7), pp. 1162-
1189, 1992.
Teh, C.H., Chin. R.T., (1988) On image analysis by the
methods of moments. IEEE Trans. Pattern Anal. Ma-
chine Intell., 10 (4), 496-513, July 1988.
Khotanzad, A., Hong, Y.H. (1990) Invariant image recogni-
tion by Zernike moments. IEEE Trans. Pattern Anal.
Machine Intell., 12 (5) , 489-498, May 1990.
INVARIANT FEATURES FOR CHARACTER RECOGNITION
107