
IMPROVING THE PERFORMANCE OF EQUALIZATION
AND A FAST START-UP TECHNIQUE FOR
COMMUNICATION SYSTEMS
Hua Ye, Wanlei Zhou
School of Information Technology
Deakin University
221 Burwood HWY, Burwood.
VIC. 3125. Australia.
Keywords: least-mean-square (LMS), discrete cosine transform ( DCT ), recursive least squares ( RLS ), filtered-X
LMS, H
2
.
Abstract: This paper explores the potential of several popular equalization techniques and proposes new
approaches to overcome their disadvantages. Such as the conventional least-mean-square (LMS )
algorithm, the recursive least-squares ( RLS ) algorithm, the filtered-X LMS algorithm and their
development. An H
2
optimal initialization has been proposed to overcome the slow convergence
problem while keeping the simplicity algorithms. The effectiveness of the methods proposed in
this paper has been verified.
1 INTRODUCTION
The least-mean-square (LMS) based adaptive
algorithm have been successfully applied in
many communication equalization practices. The
importance of the LMS algorithm is largely due
to two unique attributes(R.D.Gitlin et al., 1992):
• Simplicity of implementation
• Model-independent and therefore robust
performance
The main limitation of the LMS algorithm is its
relatively slow rate of convergence. Two
principal factors affect the convergence
behaviour of the LMS algorithm: the step-size
parameter
µ
, and the eigenvalues of the
correlation matrix R of the tap-input vector.
The recursive least-square (RLS) algorithm is
derived as a natural extension of the method of
least square algorithm. The derivation was based
on a lemma in matrix algebra known as the
matrix inversion lemma. (E.A. Lee et al., 1994). (S.
Haykin, 1996).
The fundamental difference between the RLS
algorithm and the LMS algorithm can be stated
as follows: The step-size parameter
µ
in the
LMS algorithm is replaced in RLS algorithm by
)(
1
n
−
φ
,
that is, the inverse of the correlation
matrix of the input vector U(n). This
modification has a profound impact on the
convergence behavior of the RLS algorithm in a
stationary environment, as summarized here
(David S. Bayard, 1997)-(Steven L. Gay, 1993):
1. The rate of convergence of the RLS
algorithm is typically an order of magnitude
faster than that of the LMS algorithm.
2. The rate of convergence of the RLS algorithm
is invariant to the eigenvalue spread ( i.e.,
condition number ) of the ensemble-averaged
correlation matrix R of the input vector U(n).
1. The excess mean-squared error
)(xJ
ex
of the RLS algorithm converges to zero as the
number of iterations, n, approaches infinity.
The computational load of the conventional RLS
algorithm is prohibited in real time applications.
The recursive least-squares ( RLS ) algorithm is
characterized by a fast rate of convergence that
is relatively insensitive to the eigenvalue spread
129
Hua Y. and Zhou W. (2004).
IMPROVING THE PERFORMANCE OF EQUALIZATION AND A FAST START-UP TECHNIQUE FOR COMMUNICATION SYSTEMS.
In Proceedings of the First International Conference on E-Business and Telecommunication Networks, pages 129-135
DOI: 10.5220/0001382101290135
Copyright
c
SciTePress

of the underlying correlation matrix of the input
data, and a negligible misadjustment, although
its computational complexity is increased(J.M.
Cioffi , 1984)-(BOUCHARD M., 2000).
Though the LMS algorithm does not actually
converge to the least--mean--square solution
that optimal
2
H model matching solution
achieves, they are very close if the adaptive
step size
µ
is small enough. Interestingly,
not much effort is needed to find the filter
^
P
(z) as the filtered-X LMS algorithm still
converges so long as the estimate of the
channel P (z) has less than
0
90± phase
shift and unlimited amplitude distortion. The
∞
H robust performance analysis of the LMS
algorithm conducted by Hassibi, et al. reveals
that sum of the squared errors is always upper
bounded by the combined effects of the initial
weight uncertainty (
^
W (0) --
0
W ) and
the noise
υ
( i ). This evidence strongly
supports that the
H
2
optimal initialisation
presented in this thesis can confine the error to
a low level right from the beginning and hence
improve the convergence rate dramatically.
A big benefit of this approach is that it
makes the adaptive process a virtual fine-tuning
process if a reasonable initialization is
obtained, which avoids experiencing a
possibly long adaptation process in transit to
the fine-tuning period. The advantage will
be more clearly illustrated by a high
eigenvalue spread case. Extensive simulation
experiment has shown that, in many cases,
the adaptive process starts from an
acceptable performance, and it does not need
any remedy like Discrete Cosine Transform
( DCT ) or Discrete Fourier Transform ( DFT )
even in the case with a very high input signal
eigenvalue spread where the conventional
LMS algorithm may fail and traditionally a
remedy like DCT and DFT technique is
required.
The conventional filtered-X LMS is modified
and introduced for the purpose of equalization.
Generic integration of the filtered-X structure,
LMS algorithm, RLS algorithm and
optimal
H
2
initialization is conducted to
meet all paramount criteria of simplicity,
robust and fast convergence for equalization of
high-speed, distorted communication channels.
Finally, various techniques proposed in this
thesis are tested using a popular communication
channel example, under both slight non-
stationary and sever non-stationary conditions.
Comparisons are made with other
conventional methods. Significant performance
improvement has been observed by Mont Carlo.
The effectiveness of the methods proposed in
this thesis has been verified.
2 EVALUATION
We present the experiment results of three adaptive
equalization algorithms:
least-mean-square (LMS) algorithm, discrete
cosine transform-least mean square ( DCT-LMS )
algorithm, and recursive least square ( RLS )
algorithm. Based on the experiments, we obtained
that the convergence rate of LMS is slow; the
convergence rate of RLS is great faster while the
computational price is expensive; the performance
of that two parameters of DCT-LMS are between
the previous two algorithms, but still not good
enough. Therefore we will propose an algorithm
based on H
2
in a coming paper to solve the
problems.
It is well known that high data rate
transmission through dispersive communication
channels is limited by the inter-symbol
interference (ISI). Equalization is an effective
way to reduce the effects of ISI by cancelling
the channel distortion. However, dynamic,
random and time-varying characteristics of
communication channels make this task very
challenging. High speed of data transmission
demands a low computational burden. Hence,
simplicity and robust performance play a
crucial role in equalizer design. Due to its
good robust performance and computational
simplicity, least-mean-square (LMS) based
algorithms have received a wide attention and
been adopted in most applications (E.A. Lee et
al., 1994), but one major disadvantage of the
LMS algorithm is its very slow convergence
rate, especially in high condition number case .
To solve this problem, a variety of improved
algorithm have been proposed in the literature.
Although their actual implementations and
properties may be different but the underlying
principle remains the same: trying to
orthogonalize as much as possible the input
ICETE 2004 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES
130

autocorrelation matrix and to follow a steepest-
descent path on the transformed error function.
Therefore, we extend the least square algorithm
to a recursive algorithm for the design of
adaptive transversal filter. An important feature
of the RLS algorithm is that it utilizes
information contained in the input data,
extending back to the instant of time when
the algorithm is initiated. The resulting rate of
convergence is therefore typically an order of
magnitude faster than the simple LMS algorithm.
This improvement in performance, however, is
achieved at the expense of a large increasing in
computational complexity.
The RLS algorithm implements recursively an
exact least squares solution (Steven L. Gay,
1993). At each time, RLS estimates the
autocorrelation matrix of the inputs and cross
correlation between inputs and desired outputs
based on all past data, and updates the weight
vector using the so-called matrix inversion
lemma. The DFT/LMS and DCT/LMS
algorithms are composed of three simple stages
(Steven L. Gay, 1993). First, the tap-delayed
inputs are preprocessed by a discrete Fourier or
cosine transform. The transformed signals are
then normalized by the square root of their
power. The resulting equal power signals are
input to an adaptive linear combiner whose
weights are adjusted using the LMS algorithm.
With these two algorithms, the orthogonalizing
step is data independent; only the power
normalization step is data dependent. Because
of the simplicity of their components, these
algorithms retain the robustness and
computational low cost while improving its
convergence speed.
Although the structure of the filtered-X LMS
adaptive equalization scheme is a little bit
different from that of the basic LMS adaptive
equalization scheme, the control adjustment
process is the same: adjusting the FIR model
of the equalizer to minimize the least mean
square error
k
e .
3 A FAST START-UP
TECHNIQUE
Though the LMS algorithm does not actually
converge to the least--mean--square solution
that optimal
2
H model matching solution
achieves, they are very close if the adaptive
step size
µ
is small enough. Interestingly, not
much effort is needed to find the filter
^
P (z)
as the filtered-X LMS algorithm still
converges so long as the estimate of the
channel P (z) has less than
0
90± phase
shift and unlimited amplitude distortion. The
∞
H robust performance analysis of the LMS
algorithm conducted by Hassibi, et al. reveals
that sum of the squared errors is always upper
bounded by the combined effects of the initial
weight uncertainty (
^
W (0) --
0
W ) and
the noise
υ
( i ). This evidence strongly
supports that the
H
2
optimal initialisation
presented in this thesis can confine the error to
a low level right from the beginning and hence
improve the convergence rate dramatically.
A big benefit of this approach is that it
makes the adaptive process a virtual fine-tuning
process if a reasonable initialization is
obtained, which avoids experiencing a
possibly long adaptation process in transit to
the fine-tuning period. The advantage will
be more clearly illustrated by a high
eigenvalue spread case. Extensive simulation
experiment has shown that, in many cases,
the adaptive process starts from an
acceptable performance, and it does not need
any remedy like Discrete Cosine Transform
( DCT ) or Discrete Fourier Transform ( DFT )
even in the case with a very high input signal
eigenvalue spread where the conventional
LMS algorithm may fail and traditionally a
remedy like DCT and DFT technique is
required.
The conventional filtered-X LMS is modified
and introduced for the purpose of equalization.
Generic integration of the filtered-X structure,
LMS algorithm, RLS algorithm and
optimal
H
2
initialization is conducted to
meet all paramount criteria of simplicity,
robust and fast convergence for equalization of
high-speed, distorted communication channels.
Finally, various techniques proposed in this
thesis are tested using a popular communication
channel example, under both slight non-
stationary and sever non-stationary conditions.
Comparisons are made with other
conventional methods. Significant performance
improvement has been observed by Mont Carlo.
IMPROVING THE PERFORMANCE OF EQUALIZATION AND A FAST START-UP TECHNIQUE FOR
COMMUNICATION SYSTEMS
131
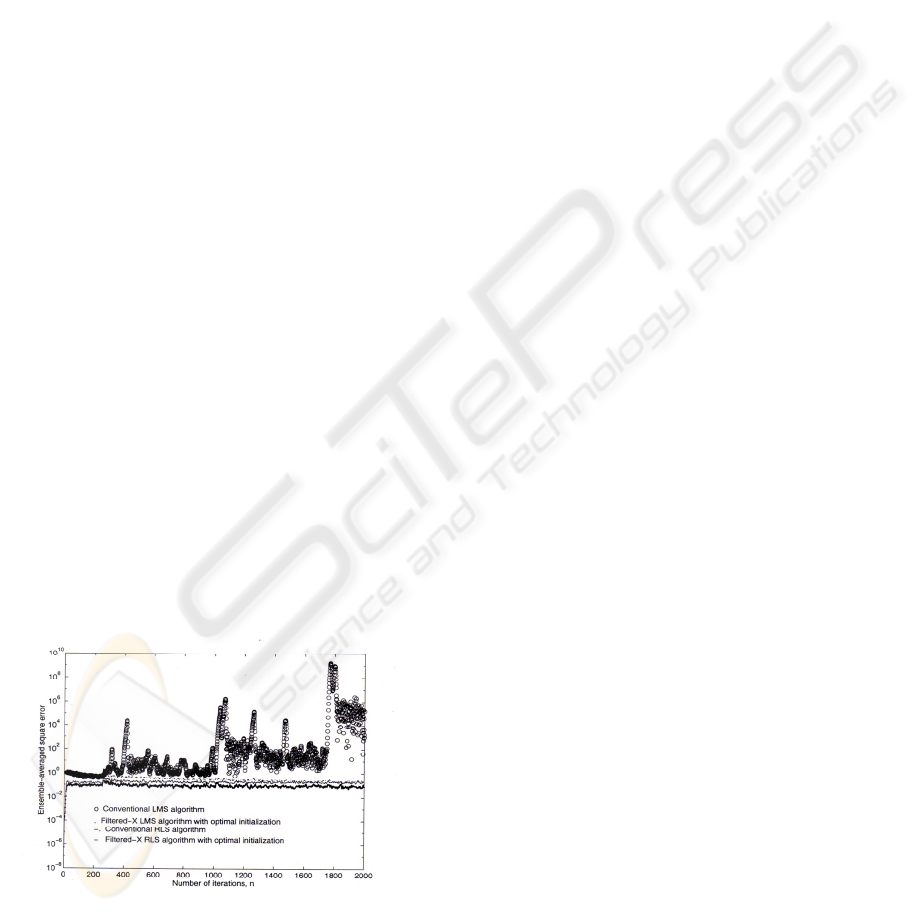
The effectiveness of the methods proposed in
this thesis has been verified.
This experiment has verified a well known fact
that the conventional adaptive LMS algorithm
can track slight non-stationary environments
such as slowly varying parameters. Now, a
more severe non-stationary situation is tested by
abruptly increasing the channel impulse
response coefficients by 35% of its nominal
value. Fig. 1 shows the simulation result.
The conventional adaptive LMS algorithm
begins to diverge while the filtered-X LMS
algorithm with or without optimal initialization
still maintains a good robust performance. The
conventional RLS algorithm still has an
acceptable performance, which matches the
observation that when the time variation of the
channel is not small, the RLS algorithm will
have a tracking advantage over the LMS
algorithm . The filtered-X RLS algorithm has a
better robust performance. The robust
performance enhancement by the introduction of
the filtered-X structure is obvious and
significant.
From a computational point of view, optimal
initialization needs an additional effort to solve
an
2
H optimal model matching or
2
H
filtering problem. Since this procedure is a
non-iterative solution and can be done off-line,
it does not increase the computational burden
in online operation. The only extra online
computational burden concerned comes from the
extra filter that is involved in every adaptive
step. However, that structure increases only a
computation of one simple algebraic
convolution. This poses no serious problem in
computation at all.
Figure 1: Learning curves of the various adaptive
algorithms experiencing a abrupt increase of impulse
response of the channel by 35%
4 INTEGRATION METHOD
Therefore, the
2
H optimal solution is actually
the limit of the best solution for the filtered-X
LMS adaptive equalization algorithm. Similar to
the case of the basic LMS adaptive
equalization scheme, the filtered-X LMS
adaptive equalization scheme can not, in
general, achieve this limit. However, its optimal
solution is still expected to be close to that
point if the adaptive size is small. Therefore,
the optimal
2
H initialization method proposed
still applies here. Why not simply use the
2
H
optimal model matching filter as the final
equalizer? This is because of the presence of
the model uncertainty and other unexpected
disturbances. The optimal solution obtained in
offline computation may not be optimal when
the filter is implemented in the real world
system because of model uncertainty and other
unexpected disturbance. For the optimal
initialization, a poorly identified system model
may give rise to a low quality model matching
solution.
However, due to robustness of filtered-X LMS
adaptive equalization scheme, this solution may
still be well within the convergence region. By
extensive simulations and experiments, it is
observed that method proposed here can also
cope with wide eigenvalue spread of the input
without having to use Discrete Cosine
Transformation (DCT) that was conventionally
required. This is an advantage in real-time
operation environment where computation
burden is a critical factor.
The focus of this work is on improving the
equalization performance of the powerful LMS
and RLS adaptive algorithms while minimizing
the increase of the related computational
complexity. Since these algorithms are very
popular in real world applications, the
attemption is significant.
Channel equalization is an effective signal
processing technique that compensates for
channel-induced signal impairment and the
resultant inter-symbol interference (ISI) in
communications system. Many sophisticated
techniques have been proposed for equalization,
most of successful real world applications are
still dominated by techniques that are related to
several popular algorithms, such as the adaptive
LMS algorithm, the filtered-X LMS algorithm
ICETE 2004 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES
132

and the RLS algorithm. For high-speed
commercial communication systems, simplicity,
robust and fast convergence rate are critical
criteria for the design of a good equalizer. The
adaptive LMS algorithm, the filtered-X LMS
algorithm, and the RLS algorithm meet some
of these criteria. Unfortunately, none of them,
alone, satisfies all these criteria. Therefore,
research on exploring the potential of these
techniques while overcoming their disadvantages
is important and necessary, which is exactly
what has been conducted in this paper.
(1). The practical importance of LMS algorithm
is largely due to simplicity of implementation
and its robust performance and its main
limitation is relatively slow rate of convergence.
The RLS algorithm is characterized by a fast
rate of convergence that is relatively insensitive
to the eigenvalue spread of the underlying
correlation matrix of the input data, and a
negligible misadjustment. Although it is
computational complexity.
(2). The conventional filtered-X LMS is
modified and introduced for the purpose of
equalization. The famous filtered-X LMS
algorithm has found very successful applications
in the field of active noise and vibration
control. It has inherited the elegant simplicity
of the conventional LMS algorithm, and is very
robust. For approach in analyzing the
performance of the filtered-X LMS algorithm, a
heuristic method based on linear time-invariant
operator theory has been provided to analyze
the robust performance of the filtered-X
structure. It indicates that the extra filter could
enhance the stability margin of the
corresponding non filtered-X structure. In this
thesis, a generic integration of the filtered-X
structure, LMS algorithm, RLS algorithm and
optimal
2
H
initialization has been conducted
to meet all paramount criteria of simplicity,
robust and fast convergence for equalization of
high-speed communication channels.
(3). To overcome the slow convergence
problem while keeping the simplicity of the
LMS based algorithms, an
2
H optimal
initialization is proposed. Though the LMS
algorithm does not actually converge to the
least-mean-square solution that optimal
2
H
model matching solution achieves, they are
very close if the adaptive step size
µ
is small
enough. Interestingly, not much effort is needed
to find the filter
(
)
zP
ˆ
as the filtered-X LMS
algorithm still converges so long as the
estimate of the channel P(z) has less than
0
90± phase shift and unlimited amplitude
distortion [21]. The
∞
H
robust performance
analysis of the LMS algorithm conducted by
Hassibi, et al. reveals that the sum of the
squared errors is always upper bounded by the
combined effects of the initial weight
uncertainty
(
)
(
)
0
0
ˆ
WW −
and the noise v(i).
This evidence strongly supports that the
2
H
optimal initialization presented in this thesis can
confine the error to a low level right from the
beginning and hence improved the convergence
rate dramatically.
A big benefit of this approach is that it makes
the adaptive process a virtual fine-tuning
process if a reasonable initialization is obtained,
which avoids experiencing a possibly long
adaptation process in transit to fine-tuning
period. The advantage will be more clearly
illustrated by a high eigenvalue spread case. As
it is well known that the conventional LMS
converges very slowly or even fails to
converge with a no matter how small adaptive
step size due to high input signal eigenvalue
spread.
2
H optimal model matching solution is
independent of this input signal eigenvalue
spread, and hence could avoid this trouble.
Moreover, this idea can be combined with
other speed-up techniques such as Discrete
Cosine Transform (DCT) and Discrete Fourier
Transform (DFT) as well as various adaptive
algorithms. Extensive simulation experiment has
shown that, in many cases, the adaptive process
starts from an acceptable performance, elated
ven in the case with a very high input signal
eigenvalue spread.
Another approach proposed here is that it
generally does not require detailed knowledge
of the external signal which is a great
advantage in practice. Since there exist many
powerful tools solving
2
H
filtering problem,
including explicit solution, the method proposed
in this thesis is very promising.
(4). A popular communication channel example
is used to test the proposed techniques, under
both slight non-stationary and severe non-
stationary conditions. The level of channel
distortion is deliberately raised to a level that
IMPROVING THE PERFORMANCE OF EQUALIZATION AND A FAST START-UP TECHNIQUE FOR
COMMUNICATION SYSTEMS
133

is much higher than any published result with
system condition number as high as nearly 390.
Furthermore, it is assumed that each tap weight
of the channel undergoes an independent
stationary stochastic process with each
parameter fluctuating around its nominal value
with a uniform probability distribution over the
interval
()
kkkk
hhhh %8,%8 +− , in
addition to the white noise disturbance of
variance 0.001 at the channel output. Mont
Carlo simulation experiment of 1000
independent trials is conducted to obtain an
ensemble-averaged learning curve. All adaptive
algorithms have shown a good robust
performance against the time varying, random
Gaussian impulse response coefficient
fluctuations specified above. The filtered-X
LMS with the optimal
2
H initialization has
been shown to have the fastest convergence
rate and best performance.
(5). A more severe non-stationary situation was
tested by abruptly increasing the channel
impulse response coefficient by 35% of its
nominal value. The conventional adaptive LMS
algorithm begins to diverge while the filtered-X
LMS algorithm with or without optimal
initialization still maintains a good robust
performance. The conventional RLS algorithm
has an acceptable performance, which matches
the observation that when the time variation of
the channel is not small, the RLS algorithm
will have a tracking advantage over the LMS
algorithm (R.D.Gitlin et al., 1992). The filtered-X
RLS algorithm has a better robust performance.
The performance improvement by using the
proposed techniques is significant and hence,
the effectiveness of the new method has been
verified.
5 CONCLUSIONS
The contributions of this paper are: we are compared
the LMS with DCT-LMS and RLS for adaptive
equalizer first, then we will be conducted on how to
speed up the convergence rate of LMS based
algorithm while keeping the increased in-line
computational burden as low as passible, we will
overcome the slow convergence problem while
keeping the simplicity of the LMS based algorithm,
and the H
2
Optimal initialization has been applied in
adaptive equalizer for communication systems.
There still exists many open problems. For
instance, the analysis of the stability margin of
the filtered-X LMS was conducted in a heuristic
manner. Can we extend this to a general case
such as a discrete time MIMO case? What about
the filtered-X RLS algorithm? Can we apply the
ideas to other adaptive equalization techniques
such as decision-feedback equalization, etc.? What
happens if we use the
∞
H optimal
initialization instead of the
2
H optimal
initialization? Another very active area of
equalization is wireless communication where the
phenomenon of fast multiple-path fading
(Rayleigh fading) is very challenging. As
indicated in the simulation, rapid and not so
small channel variations can cause the
conventional LMS algorithm to diverge. It will
be interesting and challenging, therefore, to
apply the new techniques presented here to those
areas in the future.
REFERENCES
R.D.Gitlin, J.F. Hayes, and S.B. Weinstein, Data
communication principles, Plenum Press, New York,
1992.
E.A. Lee and D.G. Messerschmitt, Digital
communication, Second Edition, Kluwer Academic
Publishers, 1994.
S. Haykin, Adaptive filter theory, Third Edition Edition,
Prentice Hall Information and System Sciences
Series, 1996.
David S. Bayard, "LTI representation of adaptive
systems with tap delay-line regressors under
sinusoidal excitation," "Necessary and sufficient
conditions for LTI representations of adaptive
systems with sinusoidal regressors," Proceedings of
the American Control Conference, Albuquer, New
Mexico, June 1997, pp. 1647-1651, pp. 1642-1646.
Steven L. Gay, "A fast converging, low complexity
adaptive filtering algorithm," Proceedings of 1993
IEEE Workshop on Applications of Signal
Processing to Audio and Acoustics, New Paltz, NY,
USA, 1993, pp.4-7.
S.Elliott and P. Nelson. "Active noise control," IEEE
Signal Processing Magazine, Oct. 1993.
Markus Rupp and Ali H. Sayed, "Robust FXLMS
algorithms with improved convergence performance,"
IEEE Trans. on Speech, Audio Processing, vol.6,
no.1, Jan.1998, pp.78-85.
E.A. Wan, Adjoint LMS: an efficient alternative to the
Filtered-X LMS and multiple error LMS algorithms.
IEEE International Conference on Acoustics, Speech,
ICETE 2004 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES
134

and Signal Processing, 1996, ICASSP-96, vol.3,
pp.1842-1845.
Markus Rupp, "Saving complexity of modified filtered-
X LMS and delayed update LMS algorithm," IEEE
Trans. on Circuits and System-II: Analog and
Digital Signal Processing, vol.44, no.1, Jan. 1997,
pp.57-60.
Steven L. Gay, "A fast converging, low complexity
adaptive filtering algorithm," Proceedings of 1993
IEEE Workshop on Applications of Signal
Processing to Audio and Acoustics, New Paltz, NY,
USA, 1993, pp.4-7.
J.M. Cioffi and T. Kailath, "Fast recursive least-squares
transversal filters for adaptive filtering," IEEE Trans.
on Acoustics, Speech, and Signal Processing, vol.
ASSP-32, pp. 304-338, April 1984.
F.T.M. Slock, "Reconciling fast RLS lattice and QR
algorithms," 1990 International Conference on
Acoustics, Speech and Signal Processing, vol.3,
pp.1591-1594, 1990, New York, USA.
M.Bouchard, S.Quednau, "Multichannel RLS Algorithms
and Fast-Transversal-Filter Algorithms for Active
Noise Control and Sound Reduction System," IEEE
Trans. Speech and Audio Processing, vol.8, no.5,
Sep. 2000
BOUCHARD, M. and QUEDNAU, S. " Multichannel
Recursive-Least-Squares Algorithms and Fast-
Transversal-Filter Algorithms for Active Noise Control
and Sound Reproduction Systems," IEEE Transactions
on Speech and Audio Processing, vol. 8. No. 5,
September 2000.
IMPROVING THE PERFORMANCE OF EQUALIZATION AND A FAST START-UP TECHNIQUE FOR
COMMUNICATION SYSTEMS
135
