
CONV2XML: RELATIONAL SCHEMA CONVERSION TO XML
NESTED-BASED SCHEMA
Angela C. Duta, Ken Barker, Reda Alhajj
Department of Computer Science,University of Calgary,2500 University Drive,Calgary, Canada
Keywords: XML, schema conversion, structural constraints, relationships, nested structure
Abstract: Conversion of relational data to XML is a critical topic in the database area. This approach translates the
rigid tabular structures of relational databases into hierarchical XML structures. Logical connections
between bits of data depicted by relationships are represented more naturally by tree-like structures.
Conv2XML and ConvRel are two algorithms for converting relational schema to XML Schema focusing on
preserving the source relationships and their structural constraints. ConvRel translates each relationship
individually into a nested XML structure. Conv2XML identifies complex nested structures capable of
modelling all relationships existent in a relational database.
1 INTRODUCTION
Most data created over the last several decades has
been stored using the relational model. Recently
XML is emerging as more prevalent in several areas
including business. This is producing an increase in
demand for tools to convert from relational
databases to XML. Much work has investigated
conversion techniques, either by translating the
entire database or only data generated by a query.
Some suggest mapping the database model to an
XML structure either using ad hoc techniques or by
using DTD or XML Schema to govern the process.
In relational databases, relationships establish
logical connections between tables. Participation and
cardinality ratios associated with each relationship
provide additional information about these
connections. This information must be translated to
XML so that the nested structures represent real data
naturally.
This paper details the conversion from the
relational schema to XML Schema (World Wide
Web Consortium, 2001). Relational relationships are
translated into nested XML structures preserving
structural constraints such as cardinality and
participation. The resulted XML structure captures
all connections between various parts of the
relational data and presents data in a suitable way for
Web publishing. The source relational database is
required to be at least in third normal form (Elmasri
and Navathe, 2003).
1.1 Contributions
The contribution of this paper is a conversion
algorithm from relational schema to XML Schema
focusing on translating relationships into nested
structures. Published data using nested structures is
easier to be read and logical connections between
parts of it are easier to be understood by users.
Relational information such as cardinality and
participation ratios of each table participating in a
relationship and how they are represented in XML is
the key element. In addition, our algorithm analyzes
the impact the existence of several relationships has
on a set of relations and how to model them in XML
using nested structures.
1.2 Paper Overview
Following this introduction, the Related work
(Section 2) considers the recent contributions in the
area of relational to XML conversion. Sections 3 and
4 introduce the ConvRel and Conv2XML algorithms
that form the primary contribution of this paper. The
paper concludes by stating conclusions and
proposing future work
210
C. Duta A., Barker K. and Alhajj R. (2004).
CONV2XML: RELATIONAL SCHEMA CONVERSION TO XML NESTED-BASED SCHEMA.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 210-215
DOI: 10.5220/0002619902100215
Copyright
c
SciTePress

2 RELATED WORK
One of the first approaches to make relational data
accessible in XML data files is DB2XML (Turau,
1999). Either the entire database or a portion is
selected through queries for transformation to XML.
SilkRoute (Fernandez, Tan and Suciu, 2000) is
considered a general and dynamic tool for exporting
relational or object-relational data to XML. It is
efficient as it combines the power of the database
query engine and features of the XML-QL query
language.
Lee et al. (Lee, et al., 2001) propose an approach
for creating nesting-based XML structures from flat
relational schema. First, the Flat Translation (FT)
converts each table into a flat element structure.
Secondly, the Nesting-based Translation (NeT)
applies the nest operator to the flat structures. The
output is an unflattened element-oriented or
attribute-oriented DTD. The unflatten process is
applied to a single table at a time and it can create
nested structures only for non-normalized tables or
for an intermediate (dependent) table in normalized
databases. The parent tables in normalized databases
are not guaranteed to have repeatable values for any
column; thus, their translation using this approach is
a flat XML structure. Unfortunately, the nest factor
used in NeT relies on the relational schema and also
the actual data stored in the database, which leads to
inconsistent results so it is somewhat unreliable.
Lee et al. (Lee, et al., 2002) (Lee, Mani and Chu,
2002) have extended the nesting approach to
multiple tables, using the CoT algorithm
(Constraints-based Translation). It is one of the first
approaches that deal with relationships. The source
database contains several interconnected tables and
based on the cardinality of the binary relationships
two types are identified 1:1 and 1:M. A directed
IND (Inclusion Dependency) Graph of tables is
created from which an empirical way to nest XML
structures is identified. A drawback of this approach
is that it includes in a nested structure only one child
relation. If there are more child relations for a
particular parent table, these relationships are
represented using IDREF.
Our approach extends the work done by Lee et
al. (Lee, et al., 2002) (Lee, Mani and Chu, 2002) in
the area of conversion from relational to XML data
by including additional elements in the analysis such
as: (1) all possible combinations of relational
structural constraint ratios; (2) M:N relationships
conversion; (3) use of XML Schema instead of
DTD which implies additional relational information
be transferred in XML; (4) a nested structure can
represent several relationships; and (5) algorithm
formalisation and its implementation in an efficient
tool.
3 THE CONVREL ALGORITHM
ConvRel analyzes each relationship to find a suitable
XML nested and compact structure to represent it. A
nested structure for a binary relationship is defined
as a pair of outer element → inner element that (1)
preserves the cardinality and participation ratios of
the relationship and (2) captures data in a single
XML root element. In addition, a structure is
compact if it uses the minimum number of XML
schema elements to represent a relationship. This
implies there exists a single complex definition for
each table.
If no XML nested and compact structure is found
then ConvRel converts each table separately and
reconstructs their relationship using keyref. Thus, all
tables and relationships from an RDBMS are
guaranteed to be translated into XML.
Several candidate XML structures, we call them
classes, are proposed using the relational
Table 1: Relationship conversion to XML.
PPR = partial participation relation. TPR = total
participation relation.
Relationship XML nested
structure
Preferred
class
(1;1):(1;1)
Parent
→ Child
Class 1
(1;1):(0;1)
PPR
→ [TPR]
Class 1 or 2
(0;1):(0;1)
Grouping
Class 3
(1;1):(1;M)
Parent
→ {Child}
Class 1
(1;1):(0;M)
Parent (PPR)
→ {[Child (TPR)]}
Class 1
(0;1):(1;M)
Child (PPR)
→ [Parent (TPR)]
Class 2
(0;1):(0;M)
Grouping
Class 3
(1;M):(1;N)
Longest Parent
→ {Intermediate
relation}
→ Shortest
Parent
Class 1
(0;M):(1;N)
PPR
→ {[Intermediate
relation]}
→ TPR
Class 1
(0;M):(0;N)
Intermediate relation
→ [Parent A]
→ [Parent B]
Class 2
CONV2XML: RELATIONAL SCHEMA CONVERSION TO XML NESTED-BASED SCHEMA
211
classification of tables in parent and child
(dependant):
• Class 1 designs the Parent → Child nested
structure (the parent table is the outer element);
• Class 2 designs the Child → Parent nested
structure (the child table is the outer element);
• Class 3 designs the XML flat structure using
keyref references;
• Class 4 designs additional Parent → Child
nested structures for the M:N relationships
modeled as a combination between a nested
structure and a keyref reference. The nested
structure models the link between one parent
and the intermediate relation and the keyref
reference models the link between the second
parent and the child.
The ConvRel algorithm converts each
relationship to an XML structure using the following
steps:
1. Identify the relationships from the RDB.
2. For each relationship determine the inner and
outer elements as follows:
a. Determine the candidate XML classes
based on the type of relationship and
structural constraint ratios for the tables
under consideration.
b. If more than one candidate class is
possible, choose the one with a nested and
compact structure; if no class is nested
and compact, transform the tables into
separate elements and restore the
relationship using keyref.
c. If there is more than one candidate class
with a nested and compact structure, then
determine the length of the generated
XML files and choose the one with the
lowest value.
d. If two or more classes have equal length
then we choose arbitrarily the one with
the Parent → Child orientation.
3. Tables not involved in any relationship are
transformed into isolated elements.
Table 1 summarizes the XML structures for each
type of relationship. XML structures are represented
schematically using notation such as: {} for
repetitive element; [] for optional element; →
followed by the inner element for subordination in a
nested structure. Case (1;1):(1;1) allows Classes 1
and 2 to be nested and compact with the same
resulting XML data file length. Arbitrarily, Class 1
is preferred as it has the Parent → Child orientation.
Case (1;1):(0;1) is transformed into Class 1 or 2,
depending on which relation participates partially in
the relationship.
The M:N relationships are between two parents
and a dependant table. Thus, in Class 1 any of the
parents can be the outer element. In Case
(1;M):(1;N), the length of a record translated in
XML from each parent must be evaluated. Case
(0;M):(0;N) considers the participation ratio of each
parent requiring the one that participates partially in
the relationship to be the outer element.
4 THE CONV2XML ALGORITHM
The ConvRel algorithm includes only a single
relationship at a time. In a real relational database
each table is connected to several other tables in a
complex structure. In this section we discuss the
influence this has on creating a nested structure for
the entire database.
For simplicity we discuss only two 1:1
relationships between three tables. First, each
relationship is converted separately to a nested XML
structure using the ConvRel algorithm. An XML
structure is then created that combines the two
previously found to obtain a nested structure, if
possible. This implies that we must identify the
cases when two nested structures combined generate
a valid nested structure.
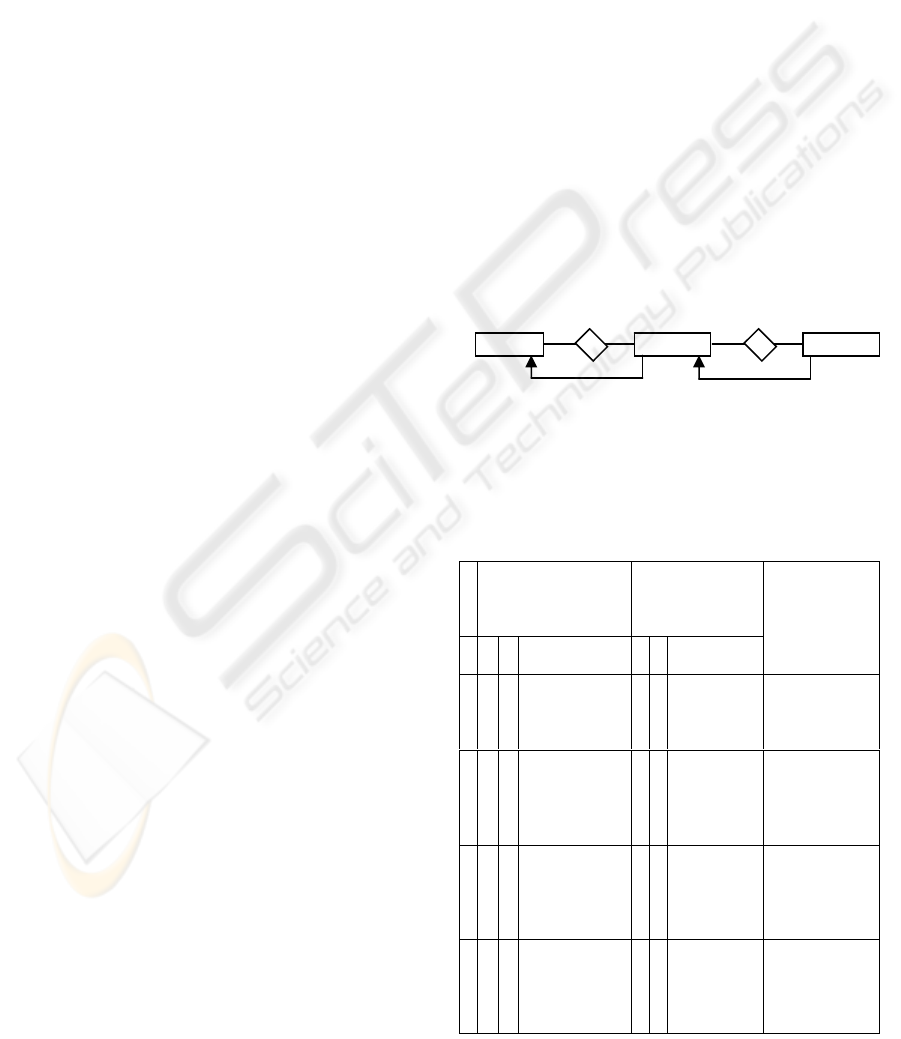
Consider the situation depicted in Figure 1 where
Table A is the parent in the first relationship and
Table B is the parent in the second relationship.
Table 2: Two relationships with a common table.
T = total participation. P = partial participation
C
a
s
e
Participation ratios in
the relationship A:B
Participation ratios
in the relationship
B:C
AB XML
representation
BC XML
representation
Relationship
A:B:C
XML
representation
1 T T A (parent)
→ B (child)
T T B (parent)
→ C
(child)
A
→ B
→ C
2 T T A (parent)
→ B (child)
Changes to:
B (child)
→ A (parent)
T P C (partial)
→ [B]
(total)
C
→ [B]
→ A
3 P T A (partial)
→ [B] (total)
T P C (partial)
→ [B]
(total)
A
→ [B]
C
keyref from C to
B
4 T T A (parent)
→ B (child)
PPB
C
keyref from C
to B
A
→ B
C
keyref from C to
B
1
1
Table A Table B
S1
1
1
Table C
S2
Figure 1: Two relationships between three tables
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
212
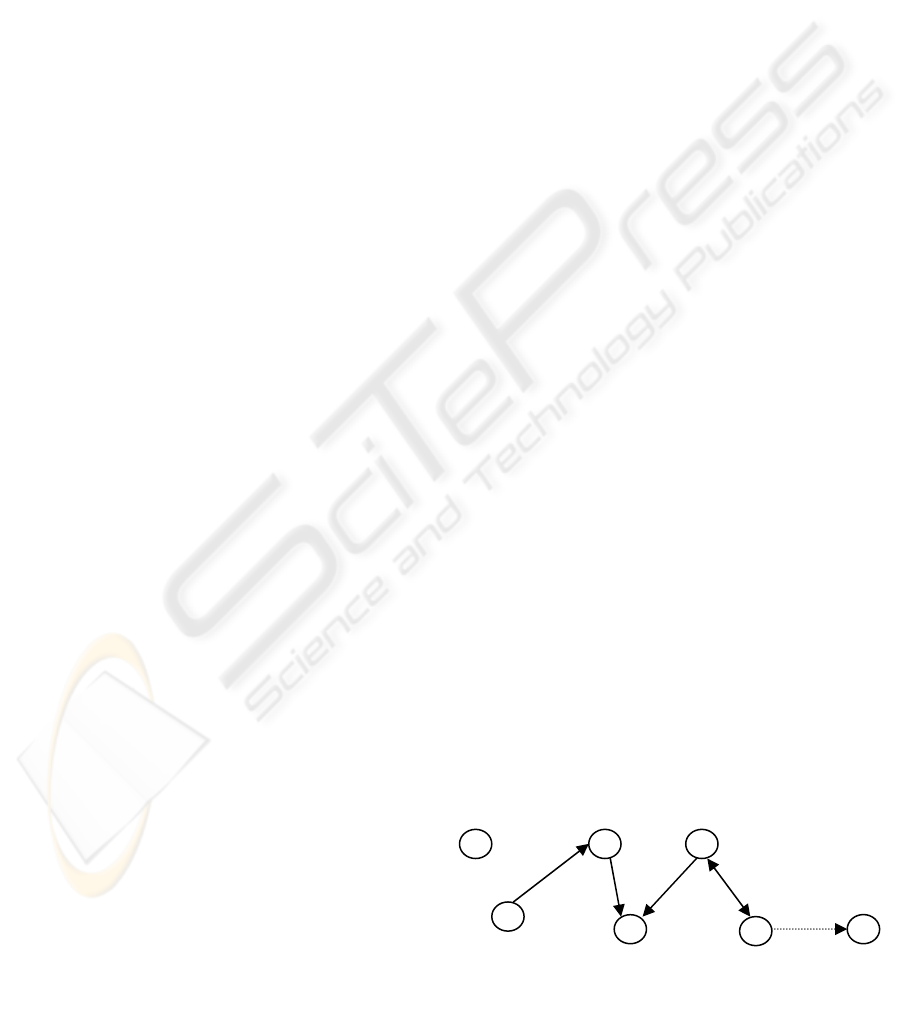
Table 2 details four cases for this situation. For each
case the resulted structure must capture and preserve
the source functional dependencies. Case 1 from
Table 2 is the nicest case where each relationship
and their combination can be modelled in a nested
XML structure. In Case 2 from Table 2 the total
relationship 1:1 between two relations A and B as
described above can be represented as Parent →
Child or Child → Parent. Both are nested and
compact XML structures and generate the same
length of XML file. We have chosen the first one, as
this is most similar to the relational model.
However, if the relations A and B are also involved
in other relationships that require some changes to
properly model them, then modelling A:B as Child
→ Parent is the preferred approach. Case 3 does not
allow a nested structure to model both relationships,
although there is a nested structure for each
relationship when considered separately. In this case
one of the relationships is represented in XML using
<keyref>. Case 4 depicts a relationship with partial
participation of both relations. In this case, the
relationship in which at least one relation has a total
participation is modelled separately. The third
relation (from the partial relationship – i.e. “C” in
Case 4 of Table 2) is added to the structure and
references are used to reconstruct the partial
relationship.
ConvRel guarantees there is a way to transform
each relationship or table from a relational schema
to an XML Schema (see (Duta, Barker and Alhajj,
2004) for more details).
It is important to analyse the tables’ involvement
in more relationships, which is accomplished by
Conv2XML. Conv2XML uses a graph
representation that combines all structures
discovered by ConvRel. The vertices are tables and
the edges represent connections between tables so
the inner element is the head and the outer element
is the tail of the arc. Note that the arcs are not
necessarily created following the orientation of the
relationships.
Two categories of edges exist in the directed
graph: (1) full edges representing links that are
modelled as nested structures, and (2) dotted edges
representing relationships that are modelled using
keyref. The last type of arc is drawn from the child
to the parent table.
In Figure 2, A is an isolated node, so it represents
a table with no relationships. The edge F→G
represents a loose connection because it can only be
modelled using keyref. The edges B→C, C→D,
E→D, and the bi-directional edge EF are full edges
that represent relationships identified by the
algorithm that can be modelled with nested
structures. This analysis is done for each relationship
separately, so there are situations when not all full
edges are incorporated in a nested structure. In the
example from Figure 2, D is the inner element of
two different elements (C and E) so it is impossible
to model with an XML nested structure without
introducing enormous amounts of redundancy. The
two possible options are: (1) a nested structure for
B→C→D, another one for E and F either as E→F or
as F→E, and a keyref for E→D; (2) a nested
structure for B→C, and a second one for E→D and
E→F (D and F are both inner elements of E). The
connection between C and D is modelled as a loose
relationship using keyref
. Both options are valid and
they are considered equivalent in terms of design.
The ConvRel algorithm is thereby transformed to
a problem of discovering trees in a directed graph.
Identifying a tree in a directed graph is efficiently
solved with the depth-first algorithm (Cormen,
2001). The depth-first algorithm is applied to full
edges only as those could generate conflicts. In the
example from Figure 2, element F has a loose
connection to G, but this does not influence the
decision of how to model other full connections
from F.
The only change to ConvRel applies to a total
relationship of type 1:1. The determining factor in
identifying the orientation for the outer element →
inner element of the relationship is its similarity to
the relational Parent → Child orientation. The Child
→ Parent modelling for this relationship type is
equivalent to the Parent → Child orientation in
terms of the nested and compact structure and the
length of the XML file (Duta, Barker and Alhajj,
2004). Thus, the conversion algorithm of a
relationship to a nested structure is altered in the
following way. If Table A participates in a total 1:1
relationship with Table B and also in other
relationships with other tables, then the graph will
have a bi-directional edge between A and B, which
allows this relationship to be modelled in connection
with other relationships. If Tables A and B are
involved only in this total 1:1 relationship then the
relationship is modelled using the similarity to the
relational orientation Parent → Child. This change
in the ConvRel algorithm creates an additional bi-
directional type of edge in the directed graph.
In summary, the conversion algorithm from
RDBMS to XML Conv2XML includes the
following steps:
A
B
C
D
E
F
G
Figure 2: A directed graph representing the links
between tables
CONV2XML: RELATIONAL SCHEMA CONVERSION TO XML NESTED-BASED SCHEMA
213

1. Determine the 1:1, 1:M, and M:N relationships
found in the relational DB.
2. Convert each relationship separately to a nested
structure using ConvRel.
3. Construct the adjacency matrix associated to a
directed graph of the database.
4. Identify the trees in the directed graph.
5. Construct the XML nested-based Schema.
a. Create the XML Schema root.
b. Create XML complex types for each relation,
excluding the foreign keys attributes for
relations represented in a nested structure.
c. Create XML complex elements for each
XML complex type and set minOccurs and
maxOccurs values according to the participation
and cardinality ratios, respectively.
d. Create the primary and unique keys using key
and unique, including only attributes that have
not been eliminated at Step 5.b.
e. Create foreign keys in the XML Schema root
using keyref for the relationships not represented
as nested structures.
XML Schema requires a root element and all
other elements are inner elements of it. There are
multiple situations when more than one nested
structure (tree) results from applying the
Conv2XML algorithm to the directed graph. This
happens for three reasons: (1) some tables are not
connected to any other table, (2) structural
constraints do not permit mapping a relationship to
any nested structure (in Figure 2, the relationship
F→G), or (3) the splitting process creates several
trees from the graph (in Figure 2, the relationships
C→D or E→D).
To ensure the XML Schema has a single root, an
arbitrary root is created using the name of the
database. This root incorporates all elements from
the structure in the same way the database contains
all tables, relationships, constraints, and indexes
from the database. The database in the relational
model and the root element from XML has similar
functions. Thus, the root element in XML Schema
contains definitions for the following elements: (1)
elements that are roots of the trees identified by
applying the depth-first algorithm; (2) isolated
elements that are not connected to any other
elements; (3) semi-isolated elements that are
connected to other elements through keyref
references and are not part of any other nested
structure.
The child table in a relationship includes the
foreign key field, which is a column taken from the
parent table. In a nested structure these foreign keys
are not required and should not appear as they cause
problems in update or delete operations due to
referential integrity constraint enforcement. Thus,
the foreign key field is eliminated from the child
table when it is transformed to an XML element if
the relationship between the parent and child table is
represented as a nested structure.
5 EXAMPLE
Consider a relational database that contains two
relations Employee (EID
, EName) and Dependant
(EID
, DID, DName). Dependant.EID is a foreign
<?xml version="1.0" encoding="UTF-8"?>
<schema xmlns=
"http://www.w3.org/2001/XMLSchema" xmlns:r=
"http://www.cps.ucalgary.ca/~duta/XMLSchema"
targetNamespace="http://www.cpsc.ucalgary.ca
/~duta/XMLSchema">
<element name="company">
<complexType>
<sequence>
<element name="emps">
<complexType>
<sequence>
<element name="emp" type="r:empType"
maxOccurs="unbounded">
<key name="depPK">
<selector xpath="deps/dep"/>
<field xpath="DID"/>
</key>
</element>
</sequence>
</complexType>
</element>
</sequence>
</complexType>
<key name="empPK">
<selector xpath="emps/emp"/>
<field xpath="EID"/>
</key>
</element>
<complexType name="empType">
<sequence>
<element name="EID" type="integer"/>
<element name="EName" type="string"/>
<element name="deps">
<complexType>
<sequence>
<element name="dep" type="r:depType"
minOccurs="0"
maxOccurs="unbounded"/>
</sequence>
</complexType>
</element>
</sequence>
</complexType>
<complexType name="depType">
<sequence>
<element name="DID" type="integer"/>
<element name="DName" type="string"/>
</sequence>
</complexType>
</schema>
Figure 3: XML Schema of the relationship Employee
→ Dependant
ICEIS 2004 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
214

key that refers to Employee.EID. The relationship is
of type Employee (1;1) : (0,M) Dependant, thus
Employee participates partially and Dependant
totally in the relationship. A complex type definition
is created for each table similar to the record
definition and is assigned to a complex element. An
additional element with the table name concatenated
with an “s” takes the role of the relation, thus
keeping the “records” grouped. Figure 3 defines two
complex types, empType and depType corresponding
to record definitions of the tables Employee and
Dependant. The complex elements emp and dep are
of the complex types previously created and act as
records within the relation- elements emps and deps.
After the elements are created, additional
constraints (i.e. primary and unique keys) are
included in the XML Schema. For inner elements of
a nested structure the structural constraints of the
former relationships are represented with minOccurs
and maxOccurs restrictions as in Figure 3. The tree
root elements have maxOccurs equal to ”unbound”
regardless of the relation’s cardinality in the
database. This ensures that the tree roots are not
inner elements of any other element, except for the
XML Schema root element. If the eliminated foreign
key column is also part of the primary key of the
child table as in the example from Figure 3, then the
primary key in the XML Schema contains the
balance of the primary attributes and the constraint
is still preserved.
In conclusion, ConvRel and Conv2XML are two
algorithms for conversion of relationships into XML
nested structures focused on preserving their
structural constraints. ConvRel translates each
relationship individually into a nested XML
structure. Conv2XML considers the implications of
relationship interconnections in a relational
database.
6 CONCLUSION AND FUTURE
WORK
This paper introduced a detailed method for
representing relational information in a tree-like
structure in XML. The algorithms use the
advantages of the relational model, such as database
normalization, relationships, cardinality and
participation ratios, exactness of relational data
types, and of the XML Schema, such as a more
natural representation in nested structures. The
method proposed is based on the depth-first
algorithm that efficiently identifies tree structures in
an oriented graph. Thus, the Entity-Relationship
Diagram associated with the relational database is
transformed so that it can model nested structures
and is analysed from the perspective of a directed
graph.
The conversion algorithms presented in this
paper have been implemented in Java version 1.3.1.
It extracts the metadata of a DB2 database and based
on additional user input for certain semantic
cardinality ratios produces a nested XML Schema.
Additional future work includes incorporating
the query metric and the XML structure evolution.
The research community has not yet agreed upon a
standard query method so it has not been included in
our method. XML’s ability to evolve and alter its
structures by adding or subtracting elements,
subelements, and attributes is an interesting feature
that has not been adequately exploited yet.
REFERENCES
Cormen, T. H., 2001. Introduction to Algorithms,
Reading, The MIT Press, 2
nd
edition.
Duta, A., Barker, K., and Alhajj R., 2004. ConvRel:
Relationship conversion to XML nested structures (to
appear). In ACM Symposium on Applied Computing
(SAC’04), Cyprus, March, 2004.
Elmasri, R., and Navathe, S. B., 2003. Fundamentals of
Database Systems, Addison-Wesley, 4
th
edition.
Fernandez, M., Tan, W.-C., and Suciu, D., 2000.
SilkRoute: Trading between Relations and XML. In
International World Wide Web Conference (WWW),
Amsterdam, Netherlands, May 2000.
Lee, D., Mani, M., Chiu, F. and Chu, W. W., 2002. NeT &
CoT: Translating Relational Schemas to XML
Schemas using Semantic Constraints. In 11th ACM
Int'l Conf. on Information and Knowledge
Management (CIKM), McLean, VA, USA, November
2002.
Lee, D., Mani, M., Chiu, F. and Chu, W. W., 2001.
Nesting-based Relational-to-XML Schema Translation.
In International Workshop on the Web and Databases
(WebDB), Santa Barbara, CA, USA, May 2001.
Lee, D., Mani, M. and Chu, W. W., 2002. Effective
Schema Conversions between XML and Relational
Models. In European Conference on Artificial
Intelligence (ECAI), Knowledge Transformation
Workshop(ECAI-OT), Lyon, France, July 2002.
Turau V., 1999. Making Legacy Data Accessible for XML
Applications. [Internet] Available from
<http://citeseer.nj.nec.com/turau99making.html>
[Accessed January 15th, 2004]
World Wide Web Consortium, 2001. XML Schema Part 0,
1, and 2. [Internet] Available from
<http://www.w3.org/TR
> [Accessed January 19th,
2004]
CONV2XML: RELATIONAL SCHEMA CONVERSION TO XML NESTED-BASED SCHEMA
215
