
MODEL-BASED COLLABORATIVE FILTERING FOR TEAM
BUILDING SUPPORT
Miguel Veloso
Enabler – Solutions for Retailing, Av. da Boavista, 1223, 4100-130 Porto - Portugal, miguel.veloso@enabler.com,
Alípio Jorge
Faculdade de Economia, Laboratório de Inteligência Artificial e Ciência de Computadores, Universidade do Porto,
R. do Campo Alegre, 823, 4150-018 Porto, Portugal
Paulo J. Azevedo
Universidade do Minho, Departamento de Informática, Campus de Gualtar, Braga, Portugal
Keywords: Data Mining, Collaborative Filtering, Recommender Systems, Association Rules, Team Building
Abstract: In this paper we describe an application of recommender systems to team building in a company or
organization. The recommender system uses a collaborative filtering model based approach. Recommender
models are sets of association rules extracted from the activity log of employees assigned to projects or
tasks. Recommendation is performed at two levels: first by recommending a single team element given a
partially built team; and second by recommending changes to a completed team. The methodology is
applied to a case study with real data. The results are evaluated through experimental tests and one survey to
potential users.
1 INTRODUCTION
The task of recommending something or someone is
very common in everyday life (Resnick et al. 1997).
This happens very often in communities, such as
consumers, users of a given Web site, or a group of
friends. If someone knows your preferences, can
recommend you a new Web site that believes you
will find of interest, or filter out another one that you
would dislike. The task of making recommendations
in a particular domain can be partially automated by
a recommender system, also known as a filtering
system, using data mining techniques.
In this work we show how a recommender
system can be used for supporting managers in
setting up a team for a given activity or project in a
company. From the activity log of employees
(resources) assigned to other projects in the past, we
build recommender models based on association
rules. Such rules can be built using standard data
mining techniques.
In the following sections we will review the
concept of recommender systems and association
rules, and then describe the problem of team
building, as well as our approach. We apply the
proposed method to real data from a company, and
evaluate the results empirically and through a survey
on users’ perception.
2 RECOMMENDER SYSTEMS
There are basically two strategies for automatically
generating recommendations: content-based and
collaborative. In content-based filtering, an item is
recommended or not, given its description or
content. This is the case if you recommend a Web
site about planet Mars to someone who likes
astronomy, because you know what the site is about.
In collaborative filtering (Goldberg et al. 1992),
we do not need to look into the content of the items.
In this case, recommender systems are built on the
assumption that a good way to find interesting
content is to find other people who have similar
interests and then recommend items that those
similar users like (Breese et al. 1998). This makes
the verifiable assumption that human preferences are
correlated (Pennock et al. 2000). In this case you
241
Veloso M., Jorge A. and J. Azevedo P. (2004).
MODEL-BASED COLLABORATIVE FILTERING FOR TEAM BUILDING SUPPORT.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 241-248
DOI: 10.5220/0002636502410248
Copyright
c
SciTePress

would recommend the Web site on planet Mars to
someone that enjoyed the site on the Hubble
telescope, not because you know these two sites are
about related issues, but because you know of other
people who have enjoyed both of them.
Recommender Systems can therefore be very
relevant in a number of business applications,
especially for increasing the number of transactions
(Sarwar et al. 2001) and improving the satisfaction
of users. In this paper we describe an application of
a collaborative recommender system for supporting
project managers in choosing team members.
A collaborative filtering recommender system
works as follows. Given a set of transactions D,
where each transaction T is of the form <id, item,
rating>, a recommender model M is produced. Each
item is represented by a categorical value while the
rating is a numerical value in a given scale (e.g. each
item is a movie rated with 1 to 5 stars). Such a
model M can produce a list of top-N recommended
items, and corresponding predicted ratings, from a
given set of known ratings (Sarwar et al. 2001). In
many situations, ratings are not explicit. For
example, if we want to recommend Web pages to a
Web site visitor, we can use the set of pages he or
she visited, assigning an implicit rate of one to those,
and zero to all the other.
In terms of collaborative filtering two major
classes of algorithms exist (Breese et al. 1998,
Sarwar et al. 2001):
Memory-based: the whole set of transactions is
stored and is used as the recommender model.
These systems employ a notion of distance to
find a set of users, known as neighbours that
tend to agree with the target user. The
preferences of neighbours are then combined to
produce a prediction or top-N recommendation
for the active user.
Model-based approaches build a model, such as
decision trees or rules, from data, which is then
used for predictions. The model can be built
using machine learning (Mitchell 1997) or data
mining (Hand et al. 2001) algorithms such as
rule-based approaches.
(Pennock et al. 2000) proposed a hybrid between
memory- and model-based approaches.
Some variants of the basic recommendation
approaches have been suggested. Sarwar et al.
(2001) explore the similarities between items rather
then users. Wei et al. (2003) employ multiple
recommendation methods. To this purpose, a system
was developed to coordinate the output of the
different methods such that only the best
recommendations were presented to the user.
Recommender systems have been applied in
many domains (e.g., Amazon.com recommends
books and CDs) (Wei et al. 2003). In (Jorge et al.
2002) they were applied to build a model-based
recommender system, based on association rules,
with the objective of improving the usability of a
web site. Such a system can produce
recommendations (links to other web pages) to each
user, on the fly, as she or he traverses the site,
according to the pages the user visits in a given
session.
3 ASSOCIATION RULES
In brief, an association rule is an expression A⇒B,
where A and B are sets of items. The meaning of
such rules is quite intuitive: given a database D of
transactions – where each transaction T∈D is a set of
items -, A⇒B expresses that whenever a transaction
T contains A than T probably contains B. This
probability is known as rule confidence and is
defined as the percentage of transactions containing
B and A relatively to the overall number of
transactions containing A. In other words, the rule
confidence estimates the conditional probability
Pr(B|A). The support of the rule is the number of
transactions that contain all elements in A∪B. The
standard algorithm for discovering association rules
from a database of transactions is APRIORI
(
Agrawal et al. 1994). The idea of mining
association rules originates from the analysis of
market-basket data where rules like “A customer
who buys products x
1
and x
2
also buys product y
with probability c%.” are found. Nevertheless,
association rules are not restricted to dependency
analysis in the context of retail applications, but are
successfully applicable to a wide range of business
problems (Hipp et al. 2000).
A recommendation model M based on
association rules corresponds to the set of
association rules generated from the user preference
data (Jorge et al. 2002). Given a set of observed
items O, the set of recommendations R provided by
M can be computed using:
R = {consequent(r
i
) | r
i
∈M and antecedent(r
i
)⊆O
and consequent(r
i
)∉O} (1)
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
242
If we want the N best recommendations (top-N),
we select from R the N recommendations
corresponding to the rules with the highest
confidence values. Another example of a
recommendation system based in association rules
was presented in (Sarwar et al. 2000).
4 TEAM BUILDING
Team building and planning is a very important
activity for companies whose structure is organized
in projects. In such a case, each sale of the company
is accomplished through a project during a certain
period. The project has a number of company’s
employees (resources) working on it. Each resource
can be assigned to more than one project
simultaneously.
Team building is a complex problem because it
requires the manipulation of a huge amount of
variables: personal and technical characteristics of
the (human) resources of the company, as well as
their availability; customer characteristics; project
characteristics; among others. Therefore, there are a
lot of generic challenges for those who have the
responsibility of doing this kind of activities:
Where is it possible to find, implicitly or
explicitly, the necessary information to perform
the team building and planning activity?
How should this information be organized in
order to facilitate its access?
Due to the dynamic and permanent growing of
companies, is it possible to concentrate this
information in some key resources? What if
these resources leave the company?
Is it possible to get a second opinion about the
choices made?
Is it possible to get an advice or a
recommendation to make a choice of this kind?
The company dimension, the number of
resources and the number and diversity of the
projects, has an obvious impact on the difficulty of
these challenges.
Let’s concentrate on the activity of human
resources in every company project, every day. We
treat resources as items, and each day of a project as
a transaction (or basket) (Figure 1 shows the
similarity with the analysis of market-basket data).
From these baskets it is possible to build a set of
association rules A⇒B with support s% and
confidence c%, with this meaning: if the resource A
works in one project / day, then B has a c%
probability to work in that same project / day.
Our working assumption is that the history of the
resources activity in every company project, every
day, implicitly contains the necessary knowledge to
perform the team building and planning activity. In
other words, such historical data can be analyzed to
unearth the past criteria used to perform the resource
selections (personal and technical resource profiles,
resource availability, project objectives and
characteristics, project success achievements and
customer characteristics). The set of association
rules should retain this implicit knowledge.
From the activity data we build a model-based
recommender system, based on association rules,
with the aim of supporting the team building and
planning process. This system receives a set of
resources as input and outputs a resource
recommendation. The overall architecture is
illustrated in Figure 2.
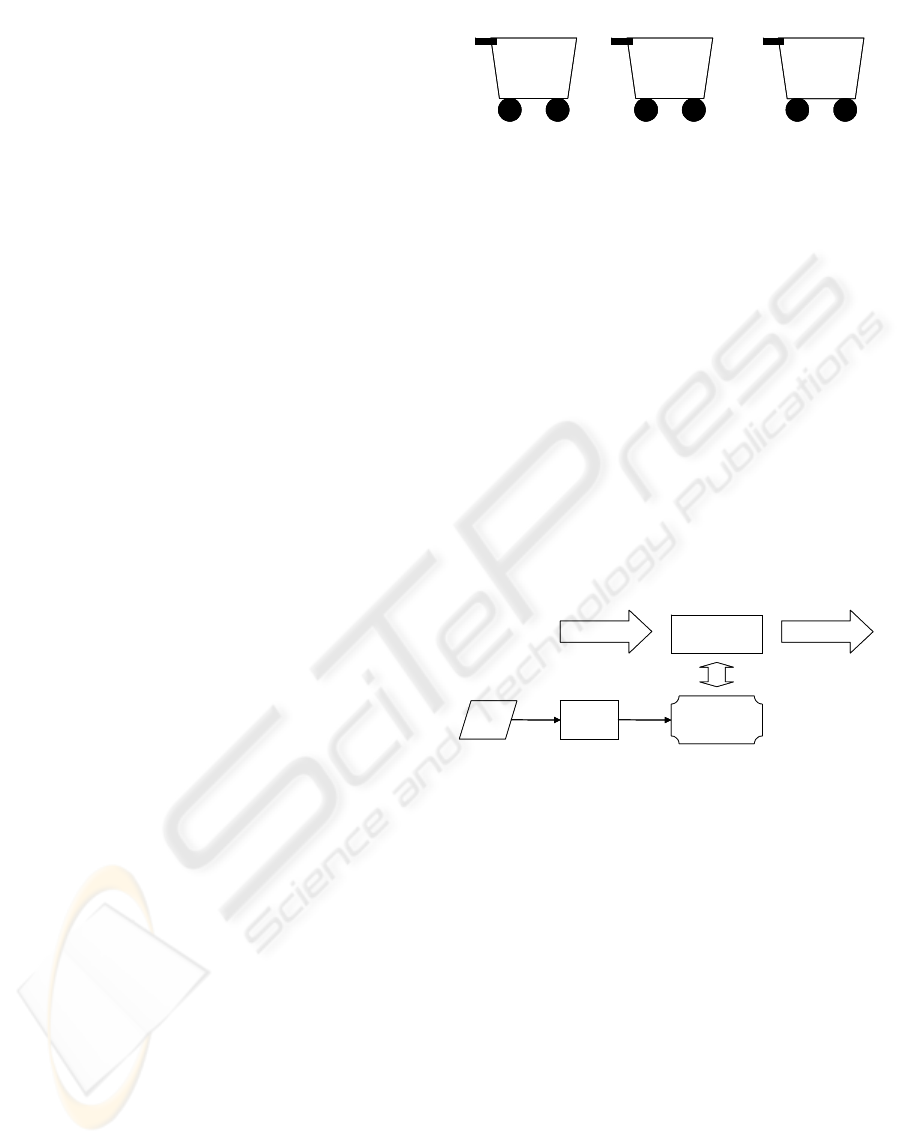
Resource
Activity
APRIORI
Set of
Association Rules
Recommender
System
Resource
Set
Recommendation
Resource
Activity
APRIORI
Set of
Association Rules
Recommender
System
Resource
Set
Recommendation
Figure 2: Team Building Recommender System
architecture.
From this functionality – Resource
Recommendation – we can build another one:
Resource Team Recommendation. Basically we can
describe it like this: given the resource team {a
1
, a
2
,
…, a
n
} as input, this functionality recommends
another team, with the same number of resources,
changing one single resource a
k
by another one - b -
that this system considers more appropriate
(according to the rules found from the activity data).
This new resource b has the same technical
characteristics as a
k
. For example: given the resource
team {x, y, z}, this functionality could recommend
the new team {x, k, z} where k has the same
technical characteristics of y.
The aim of this new functionality is to give the
manager in charge of the team building task an
opportunity to improve one resource team
previously built.
The team recommendation algorithm (
Veloso, M.
2003
) assumes that the resources are characterized
•John
•Louis
•James
•Rose
•
John
•Camilla
•Rose
•Gabriel
...
Project: A
Day: 1 July 2002
Project: A
Day: 2 July 2002
Project: B
Day: 1 July 2002
•John
•Louis
•James
•Rose
•
John
•Camilla
•Rose
•Gabriel
...
Project: A
Day: 1 July 2002
Project: A
Day: 2 July 2002
Project: B
Day: 1 July 2002
Figure 1: Resource activity viewed as a market-
basket problem.
MODEL-BASED COLLABORATIVE FILTERING FOR TEAM BUILDING SUPPORT
243
by a career level, which roughly corresponds to their
level of expertise, and by a resource pool – that
contains the set of resources with specific technical
competences, such as “information systems”,
“marketing”, and so on. Recommended
replacements must satisfy the restriction that the
career level and the resource pool must be the same
of the replaced element.
Team_Recommendation(e)
/* e = {r
1
,…,r
n
} – team that we want to
optimize */
for each sub team e
i
/* e
i
is a sub team of e with size =
[(size of e) – 1], by taking out
the resource r
i.
*/
generate all resource
recommendations given e
i
choose the best of these
recommendations, from the
same resource level and
from the same resource pool
as r
i
/* the best recommendation
corresponds to the rule
with the highest confidence
*/
among the [size of e]
recommendations selected on the
previous cycle, chose the one with
the highest confidence
recommend the team formed by the e
i
sub team
that has originated the
recommendation selected on the
previous step, and the associated
recommendation
This algorithm can be iterated, and produce more
than one replacement on the initial team.
5 EMPIRICAL RESULTS
These concepts have been applied to real data from a
systems integrator company: Enabler – Solutions for
Retailing
1
. This company belongs to SONAE
economic group and its main activity is to sell
Information Technology projects for retailers
operating in the European Union and Brazil.
Enabler uses a software application – Service
Sphere from Evolve
2
- to log time spent on projects
(time reports). Every Enabler resource must log its
own time report every week for control and
1
www.enabler.com
2
www.evolve.com
management purposes. These time reports store
information about the resource activity in the various
company projects - they represent the history of
resources activity mentioned in the previous section.
The time report data was loaded into a MySQL
3
database. Then, to create the set of association rules
we used CAREN (Azevedo 2003). The recommender
models were implemented in R
4
, a statistical
environment and programming language (Ihaka and
Gentleman, 1996).
To evaluate empirically the resource
recommendation models generated, we split
randomly the baskets into train and test sets (we
chose an 80% / 20% split). The training set is used
to generate the recommendation model. From each
basket in the test set we randomly delete one
resource. The set of deleted resources is called the
hidden set (Hidden). The set of baskets with the
remaining resources is called the observable set
(Observable). Breese et al. (1998) named this
evaluation set-up procedure the All But One
Protocol.
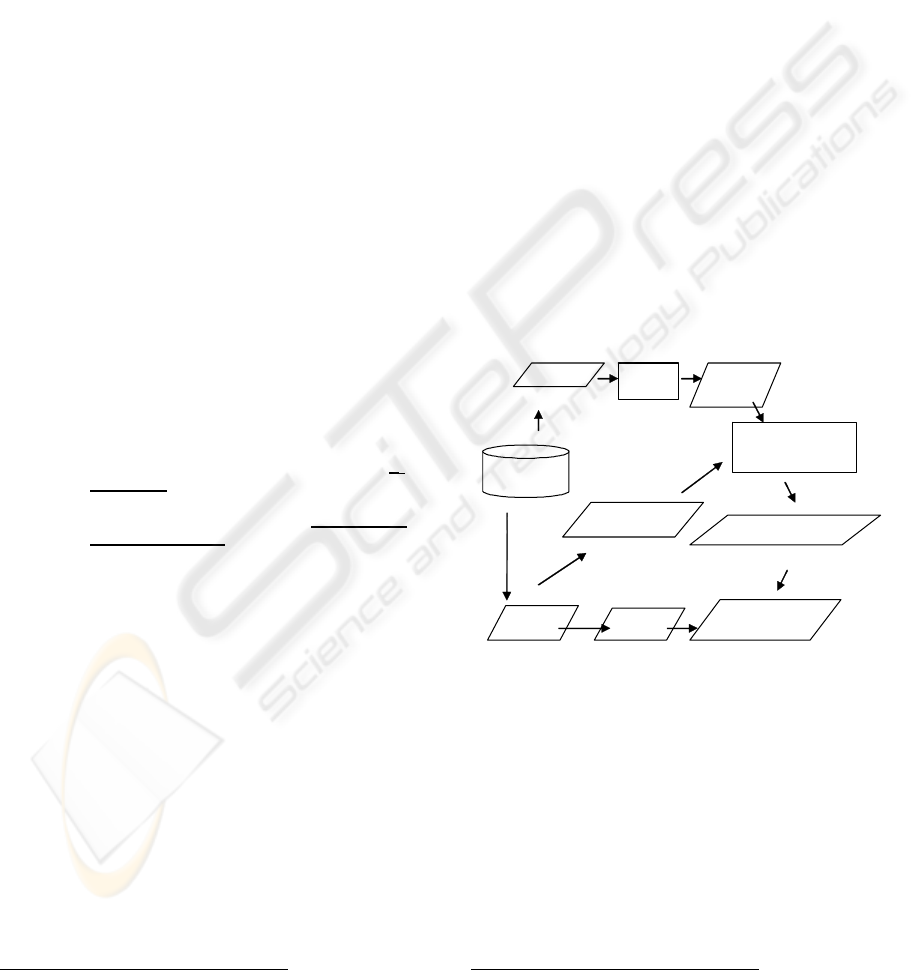
One recommender model is evaluated by
comparing the set of N recommendations it makes
(Rec), given the Observable set, against the
resources in the Hidden set (Figure 3).
Baskets
Train
Test
Observable
Hidden
Recommendation
System
Recommendations
Evaluation
Metrics
Caren Set of
Rules
Figure 3: Steps required to perform the recommendation
system empirical evaluation.
Several types of quality measures have been
proposed for evaluating a recommender system. We
have adopted measures typically used for
information retrieval tasks namely recall, precision
and F1 (van Rijsbergen 1979). These measures are
also common for the evaluation of recommender
systems (Breese et al. 1998), (Sarwar et al. 2000),
(Jorge et al. 2002).
Recall is a global measure for the whole set of
baskets in the test set. It corresponds to the
proportion of relevant recommendations that have
3
www.mysql.com
4
www.r-project.org
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
244
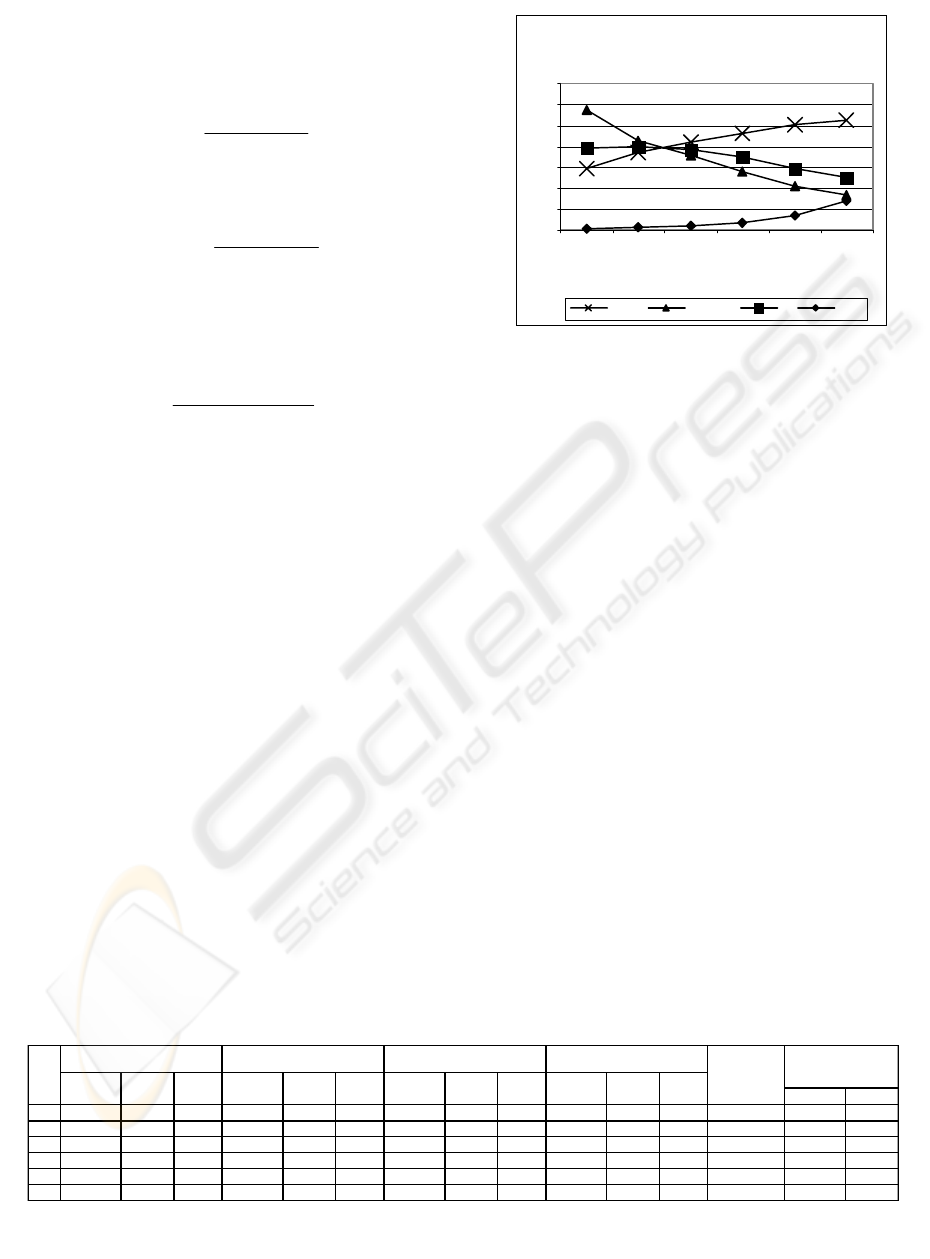
Table 1: Results for recall, precision and F1, for different N values. Recall values for random guess (RND), as well as recall
and precision for default guess are also shown
Recall Prec.
1 0,147 0,287 0,194 0,089 0,277 0,134 0,091 0,425 0,150 0,054 0,360 0,093 0,003 0,011 0,019
2 0,194 0,288 0,201 0,106 0,213 0,142 0,100 0,352 0,155 0,059 0,299 0,098 0,007 0,017 0,015
3 0,217 0,168 0,189 0,115 0,189 0,143 0,103 0,318 0,155 0,061 0,269 0,099 0,010 0,029 0,013
5 0,240 0,129 0,168 0,121 0,163 0,139 0,105 0,282 0,153 0,063 0,241 0,100 0,017 0,034 0,012
10 0,261 0,095 0,140 0,125 0,138 0,131 0,109 0,252 0,152 0,065 0,218 0,101 0,034 0,057 0,010
20 0,272 0,076 0,119 0,127 0,128 0,128 0,111 0,236 0,151 0,066 0,210 0,101 0,069 0,108 0,009
N
Prec. Prec.Recall RecallPrec.Recall Prec. F1
(Recall)
RND
Default
F1
minsup=0,003
minconf=0,1
minsup=0,005
minconf=0,5
F1
minsup=0,005
minconf=0,1
minsup=0,003
minconf=0,5
F1Recall
been retrieved by the system, i.e., the proportion of
resources in the hidden set that are adequately
recommended. The value of recall tends to increase
with N, the number of recommendations made for a
single team.
||
||
Hidden
RecHidden
Recall
∩
=
Precision gives us the average quality of an
individual recommendation. As N increases, the
quality of each recommendation decreases.
||
||
Rec
RecHidden
Precision
∩
=
F1 has been suggested as a measure that
combines recall and precision with equal weights. It
ranges from 0 to 1 and higher values indicate a more
balanced combination between recall and precision.
It is useful as a summary of the other two measures.
PrecisionRecall
PrecisionRecall
F1
+
××
=
2
The data used in these experiments refer to the
period between September 2001 and November
2002. For this period we have 290 resources and
26234 baskets. The average number of resources per
basket is 2,68. With the train and test split we got
20987 baskets for train set and 5247 baskets for test
set.
To build the set of association rules we tried
different combinations of minimum support and
minimum confidence. Table 1 shows the results for
recall, precision and F1, for different N values. The
best results for recall were achieved with minimum
support = 0,003 and with minimum confidence = 0,1.
For these parameters, the number of rules in the
model was 8957.
Recall is around 15% when only one
recommendation is made (N = 1) – this means that
we are able to retrieve 15% of the relevant
recommendations. In this case, precision is higher
(0,287) because a recommendation is not made
when no rule applies. The recommender model
recall value is 49 times higher than the resource
random guess (Rnd column). These random values
were obtained by dividing N by the total number of
resources (290).
We have also compared the predictive accuracy
of our model with the default recommendations (the
most likely resources a priori). When N = 1, the
default recommendation for every basket in the
observable set is the resource with the highest
support in the training set; when N = 2, the default
recommendations for every basket in the observable
set are the two resources with the highest support in
the train set, and so on. In Figure 5 we can see the
comparison of recall values between our model and
default recommendations, for different N values.
In the case of precision, it drops smoothly as the
number of recommendations N increases, as it was
expected. When N = 1 each one the collaborative
filtering recommendations made has a 28,7% chance
of being relevant. In Figure 6 we can see the
comparison of precision values between our model
and default recommendations, for different N values.
The F1 measure indicates that the best
combination of recall and precision is achieved
when N = 2. This can be used if we want to give the
team manager a list of recommendations with a good
balance between recall and precision.
Minsup=0,003 Minconf=0,1
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
12351020
N
Recall Precision F1 RND
Figure 4: Results for recall, precision and F1, for
different N values – minimum support=0,003 and
minimum confidence=0,1.
MODEL-BASED COLLABORATIVE FILTERING FOR TEAM BUILDING SUPPORT
245

Since many of the baskets in the data set have
one resource only, it is relevant to know how does
the predictive performance of the model change
when such baskets are not taken into account for
model evaluation. This makes sense because when a
basket with one resource only is used for testing,
that single resource is hidden and the model makes
a recommendation on the basis of no information.
This is unrealistic, since we do not expect the
resource recommender system to be used under such
conditions.
To do this we discarded baskets with only one
resource and obtained new values for recall,
precision and F1. These results are showed on Table
2. As we can observe, recall values increase visibly
under these more realistic conditions (for N = 5, for
example, recall is about 42%).
Table 2: Results for recall, precision and F1, for
different N values, when baskets with only one resource
are discarded. Recall values for random guess (RND), as
well as recall and precision for default guess are also
shown
We should also point out that this experimental
evaluation procedure can be pessimistic in many
situations since recall and precision measures only
consider as correct the recommendations that exactly
match the hidden one. The fact that a
recommendation is not exact, does not mean that it
is not adequate. Consider the following example:
suppose we hide for testing the resource c from the
basket with resources {a, b, c}. Therefore {a, b} is
the observable basket and {c} is the hidden basket.
If we apply the resource recommendation
functionality to the observable basket and if it
recommends the resource d, this mean that this
recommendation will not contribute positively to the
recall value (due to the fact that |{c}∩{d}| = 0). But
this does not mean that {d} is not an adequate
recommendation for the {a, b} team.
For that reason, we decided to confront the
decisions made by our collaborative filtering
recommender model to its potential users.
6 USERS’ PERCEPTION
For further evaluation of the system, we conducted a
survey to study the perception of its potential users
regarding the adequacy of the recommendations
made. We used a sample of 17 resources (among a
universe of 56 potential users of this system).
The survey was divided into two parts
(corresponding to the two functionalities of this
system):
• Resource recommendations – 6 randomly
generated resource teams were presented. For
each of them it was applied the resource
recommendation functionality. We then asked
the sampled resources to express their
perception about the adequacy level of the
recommendations made.
• Resource team recommendations - 6 randomly
generated resource teams were presented. For
each one of them it was applied the resource
team recommendation functionality. We then
collected the opinions about the adequacy of
the recommendations presented.
The adequacy level was measured according to
the following scale:
0
0,1
0,2
0,3
0,4
12351020
N
Precision Precision (Default)
Figure 6: Comparison of collaborative filtering
results with default recommendations (Precision)
Recall Prec.
1 0,255 0,287 0,270 0,003 0,011 0,019
2 0,338 0,288 0,257 0,007 0,017 0,015
3 0,378 0,168 0,233 0,010 0,029 0,013
5 0,418 0,129 0,197 0,017 0,034 0,012
10 0,455 0,095 0,158 0,034 0,057 0,010
20 0,474 0,076 0,131 0,069 0,108 0,009
(Recall)
RND
Default
Recall Prec. F1
N
minsup=0,003
minconf=0,1
0
0,05
0,1
0,15
0,2
0,25
0,3
12351020
N
Recall Recall (Default)
Figure 5: Comparison of collaborative filtering results
with default recommendations (Recall)
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
246

1 – Very Inadequate.
2 – Inadequate.
3 – Neither Inadequate, Nor Adequate
4 – Adequate.
5 – Very adequate.
The survey results were compiled in order to
obtain the average level of the adequacy perception.
We also show a 95% confidence interval for the
population means:
Table 3: Users’ perception survey compiled final
results show the average opinion of the users about the
adequacy of recommendations. The limits of the 95%
confidence interval are also shown
Average
Inf. Sup.
Resource Recommendation
3,31 3,03 3,59
Team Recommendation
3,80 3.59 4,02
95%
Confidence
Interval
With these results we can conclude, with a 95%
confidence, that the potential users of this
recommendation system have an average positive
perception of the adequacy of the recommendations
made, especially for the team recommendation
facility.
7 CONCLUSIONS
We proposed a new method to support the team
building and planning process in a company or
organization. To implement this method we
developed a model-based recommendation system,
based on association rules built on operational data
about the resources real activity. The choice of
association rules follows the assumption that these
data implicitly store relevant knowledge to this
building and planning process; as well as the
assumption that the set of association rules found are
able to represent that knowledge.
With this system it is possible to get a second
opinion about a resource choice previously made
and it is also possible to get an advice, or a
recommendation, to perform a choice of this kind.
The experimental results, as well as the analysis
of the users’ perception showed this approach has a
positive impact on the team building task.
This kind of system can be implemented in any
organization that stores information about the real
resource activity. In the case of the organization that
provided the data the process of information
collection does not represent any extra cost since it
had been done previously for management control
purposes.
The company dependency on some key resources
that usually concentrate a lot of information
necessary to perform team building and planning
activities could be minimized with a system with
these characteristics.
We demonstrate the applicability of association
rules and collaborative filtering recommender
systems in a different domain: team building and
planning.
Our approach could be improved by allowing the
manager the specification of more constraints to the
recommender system, in addition to the career level
and resource pool constraints. One useful feature
would be the special treatment of new resources that
do not appear in historical data.
ACKNOWLEDGEMENTS
We would like to thank to Jorge Brás (CEO Enabler
Portugal) for his permission to use Enabler real data
in this paper. A special thanks to Jorge Santos and
José Ribas (Enabler Portugal Competency Centre
Managers) for all their support. And, finally, a very
big thanks to the Enabler staff that kindly
participated on the survey that was presented.
This work has been supported by the
POSI/SRI/39630/2001/Class Project (Fundação
Ciência e Tecnologia), FEDER e Programa de
Financiamento Plurianual de Unidades de I & D.
REFERENCES
Agrawal, R. e Srikant, R. (1994), “Fast Algorithms for
Mining Association Rules”. In Proc. of the 20th Int’l
Conf. On Very Large Databases (VLDB’94),
Santiago, Chile, June 1994.
Azevedo, P. J. (2003), “CAREN – A Java Based Apriori
Implementation for Classification Purposes”.
Technical Report, January 2003. Accessed on March
30th 2003 www.di.uminho.pt/~pja/class/caren.html
Breese, J. S., Heckerman, D. and Kadie, C. (1998)
“Empirical Analysis of Predictive Algorithms for
Collaborative Filtering”. Appears in Proceedings of
the Fourteenth Conference on Uncertainty in Artificial
Intelligence, Madison, WI, July, 1998. Morgan
Kaufmann Publisher.
Goldberg, D., Nichols, D., Oki, B. M. and Terry, D.
(1992), “Using Collaborative Filtering to Weave an
Information Tapestry”. Comun. ACM 35, 12 (Dec.
1992), 61 – 70.
Hand, D. J., Mannila, H. and Smyth, P. (2001), Principles
of Data Mining, MIT Press.
MODEL-BASED COLLABORATIVE FILTERING FOR TEAM BUILDING SUPPORT
247

Hipp, J., Guntzer, U. e Nakhaeizadeh, G. (2000),
“Algorithms for Association Rule Mining – A General
Survey and Comparison”. SIGKDD 2000.
Ihaka, R., Gentleman, R. (1996), “R: A Language for Data
Analysis and Graphics”, Journal of Computational
Graphics and Statistics,Vol. 5, N. 3, pp. 299-314.
Jorge, A., Alves, M. A. and Azevedo, P. (2002),
“Recommendation With Association Rules: A Web
Mining Application”, in Proceedings of Data Mining
and Werehouses, a sub-conference of information
society 2002, EDS. Mladenic, D., Grobelnik, M., Josef
Stefan Institute, October 2002.
Mitchell, Tom M., (1997), Machine Learning, WCB /
McGraw-Hill.
Pennock, D. M., Horvitz, E., Lawrence, S. and Giles C. L.
(2000), “Collaborative Filtering by Personality
Diagnosis: A Hybrid Memory – and Model – Based
Approach”. In Proceedings of the Sixteenth
Conference on Uncertainty in Artificial Intelligence
(UAI-2000), pp. 473-480, Morgan Kaufmann, San
Francisco, 2000.
Resnick, P. and Varian, H. (1997), “Recommender
Systems”. Communications of ACM, Vol. 40, No. 3,
March 1997.
Sarwar, B., Karypis, G., Konstan, J. and Reid, J. (2000),
“Analysis of Recommendation Algorithms for E-
Commerce”. In Proceedings of the ACM EC’00
Conference. Minneapolis, MN. pp. 158-167.
Sarwar, B., Karypis, G., Konstan, J. and Reid, J. (2001),
“Item-based Collaborative Filtering Recommendation
Algorithms”. Appears in WWW10, May 1-5, 2001,
Hong Kong.
van Rijsbergen, C. A. (1979), Information retrieval.
London: Butterworths.
Veloso, M. (2003), “Regras de Associação Aplicadas a um
Método de Apoio ao Planeamento de Recursos
Humanos” (in portuguese), MSc. Thesis (submitted),
Mestrado em Análise de Dados e Sistemas de Apoio à
Decisão, Faculdade de Economia, Universidade do
Porto.
Wei, Y. Z., Moreau, L. and Jennings, N. R. (2003),
“Recommender Systems: A Market-Based Design”.
Proc. 2nd International Joint Conference on
Autonomous Agents and Multi Agent Systems
(AAMAS03).
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
248
