
DESIGN AND IMPLEMENTATION OF A SCALABLE
FUZZY CASE-BASED MATCHING ENGINE
RAMI HANSENNE, JONAS VAN POUCKE, VEERLE VAN DER SLUYS
Actonomy NV, Stapelplein 70, B – 9000 GENT (Belgium)
BARTEL VAN DE WALLE
Department of Information Systems and Management, Tilburg University
K
eywords: Case-based reasoning; fuzzy set theory; matching engine; matching techniques.
Abstract: We discuss the design and the implementation of a flexible and scalable fuzzy case-based matching engine.
The engine’s flexible design is illustrated for two of its core components: the internal representation of cases
by means of a variety of crisp and fuzzy data types, and the fuzzy operations to execute the ensuing case
matching process. We investigate the scalability of the matching engine by a series of benchmark tests of
increasing complexity, and find that the matching engine can manage an increasingly heavy load. This
indicates that the engine can be used for demanding matching processes. We conclude by pointing at several
applications in experimental electronic markets for which the matching engine currently is being put to use,
and indicate avenues for future research.
1 INTRODUCTION
Case-based reasoning (CBR) is a problem solving
approach resembling an example-based search
process. Problems that have been encountered earlier
are stored as examples, and when confronted with a
new problem, similar problems from this set are
identified by means of a search process. The query
(or target) problem is then classified according to the
similarity of earlier examples that have been
identified (Kolodner, 1993). More formally, CBR
can be defined as a four-step process (Aamodt and
Plaza, 1994):
• Retrieve: Given a target problem, relevant
stored cases are retrieved. A case consists of a
problem, its solution, and, typically, annotations
about how the solution was derived.
• Re-use: Map the solution from the previous case
to the target problem. This may involve
adapting the solution as needed to fit the new
situation.
• Revise: Having mapped the previous solution to
the target situation, test the new solution in the
real world (or a simulation) and, if necessary,
revise.
• Retain: After the solution has been successfully
adapted to the target problem, store the resulting
experience as a new case in memory.
The CBR process in general and the retrieval phase
in particular are the focus of the matching engine we
describe in this paper. The general design principles
that have guided the development of the matching
engine are presented in the following section, as well
as the case matching pipeline we have constructed.
Section 3 focuses on the internal workings of the
matching process, for which various operators
derived from fuzzy set theory are used. Section 4
investigates the scalability of the fuzzy matching
engine, by varying the case complexity and the
number of cases. We conclude in Section 5 by
presenting relevant enterprise matching applications
and indicating future research opportunities and
challenges.
375
HANSENNE R., VAN POUCKE J., VAN DER SLUYS V. and VAN DE WALLE B. (2004).
DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 375-382
DOI: 10.5220/0002645903750382
Copyright
c
SciTePress

2 DESIGN OF THE MATCHING
ENGINE
While our focus in this paper is on case-based
reasoning problem solving, it must be noted that it
was our overall design goal to develop a generic
framework for reasoning about data, and to allow
extensions of our framework towards other AI
technologies, such as clustering, re-inforcement
learning, neural networks and expert systems (Pal et
al., 2001).
2.1 Design layers overview
2.1.1 Algorithm Layer
This layer is concerned with the actual
implementation of the matching algorithms.
Moreover, Layer 1 controls the scalability of the
engine, e.g. by running certain matching algorithms
in parallel. To the end user, the Algorithm Layer is
the most abstract layer: there is no graphical user
interface (GUI) to directly interact with this layer.
The functionality of this layer is, in short, restricted
to matching one data set to another. This layer does
not ‘know’ where the data sets come from, or where
they will be further processed. This is taken care of
by the second layer, the Management Layer.
2.1.2 Management Layer
The Management Layer is an intermediate layer
between the Algorithm Layer and the Application
Layer and makes abstraction of the communication
between these two layers. This layer provides
management functionality to the matching engine,
for example security, data import from files, data
bases or data stores, user management, etc. This
layer must enable those users who have no specific
technical knowledge about the matching algorithms
or the structure of the datasets to work with the
matching engine.
2.1.3 Application Layer
The Application Layer, is the front end of the
software engine application. Layer 3 contains the
software which actually makes use of the matching
engine, and can add its own functionality to the
application. Dedicated GUIs can be developed and
other applications can be integrated within this layer.
Other applications such as search engines, web
services or autonomous agents can make use of the
data that have been matched.
2.2 The matching engine pipeline
The flow of the fuzzy matching engine as shown in
Figure 2 below can in essence be viewed as a
traditional input - output process, where the input
consists of one or more cases (the actual query), the
process is the fuzzy matching process, and the
output consists of the cases that have been matched
(the actions). This process is iterative: the output of
the process can be fed back into the engine, and re-
used for a subsequent or new matching query.
The different steps in the ‘pipeline’ of Figure 2 are
elaborated below. In principle, every step should be
individually configurable (at startup time and run
time), and controlled by a “step manager”. We are
currently exploring the development of a separate
workflow engine which controls each step of the
process and also indicates which loop-backs should
be performed.
2.2.1 Cases
Cases are the start of the process and are typically
created in Layer 2, the Management Layer. A case is
defined as a set of different properties, with every
property describing a single attribute on which a
matching is requested. Any property can have one of
the following formats: Boolean, Ordinal
(qualitative), Numeric (quantitative), Alpha numeric,
Fuzzy (vague) or Unknown. These properties are
extensible, as we do not know beforehand which
other data types may be needed. We only know that
they are atomic and that they form the basis upon
which will be matched. Properties also have meta-
information. They can have a weight to describe the
importance of an individual property, a ranking
relative to other properties and a veto power on other
properties that are not compatible. Some properties
can be converted into another format. For example, a
Numeric property is a special case of a Fuzzy
property, and hence could be converted into a Fuzzy
one without loss of precision or information. Cases
are stored in memory, which can be persistent or
transient.
Figure 1: The matching engine pipeline
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
376
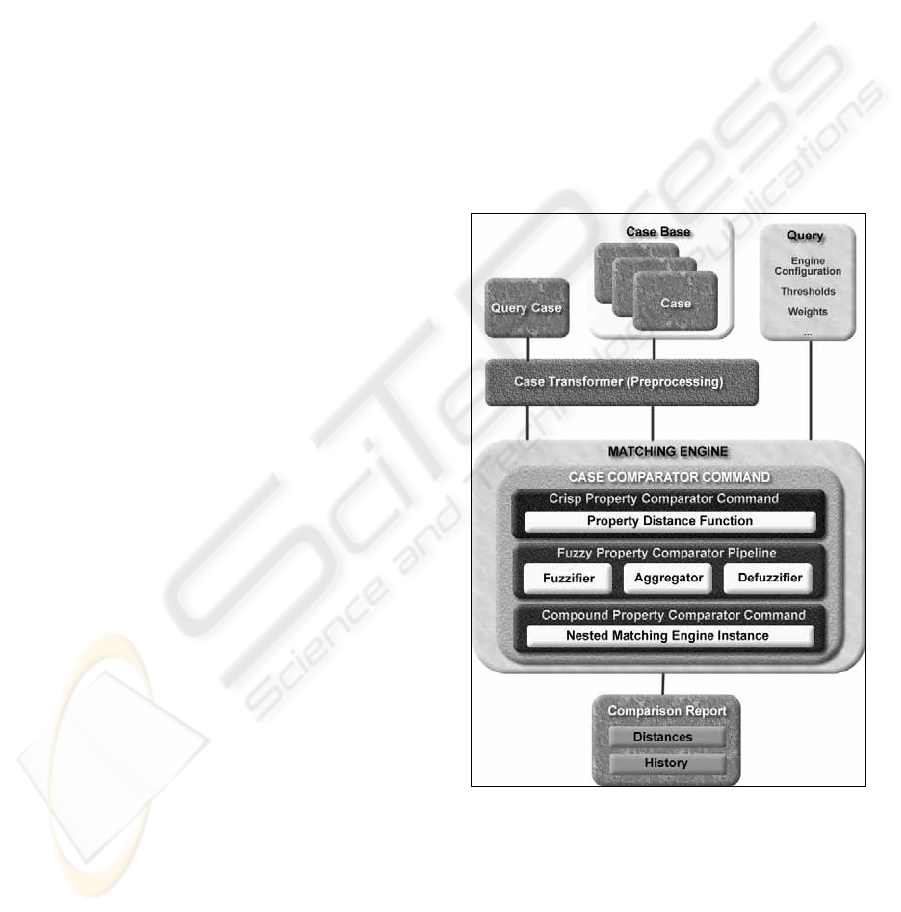
2.2.2 Pre-processing
The pre-processing step occurs before the actual
matching. While this step is not part of the actual
matching algorithm, it is, globally speaking, part of
the matching process. This step is not intended to
create cases or do property extraction from some
source, but rather to do some manipulation on the
properties of a case. The pre-processing is a queue
of zero, one or more pre-processing steps, but each
step is independent of the other. As such, they run
sequentially in a well defined order. The pre-
processing is not required; actually, a valid
implementation is one that simply let pass all cases
without modifying them.
2.2.3 Matching
The matching step is the heart of the workflow. Here
we select the algorithm to match cases against
others. The actual implementation can differ, and
one could choose for a simple sorting of cases or
instead perform complex clustering algorithms. For
our purposes, there are some requirements upon the
matching step. We must be able to handle unknown
and incomplete data, or more specifically, we must
be able to handle cases where some or more
properties are absent, unknown or invalid. As a
result of the matching step, we obtain a result or
conclusion. This result can be partially complete, but
it always has received a score which indicates how
well the case matches with other cases.
2.2.4 Post-processing
The post-processing step acts on the result of the
matching step and is optional, as was the pre-
processing step. In this step, for instance, we could
decide to store intermediate results.
2.2.5 Selection of actions and matching
loops
In principle, the workflow process could run in an
endless loop: the result of the matching step can be
fed again into the initial ‘cases’ step. However, an
action is associated with the conclusion of every
single loop. This allows us to act upon partial results
that have been obtained during the matching or
reasoning. The main reason for having a loop is to
make the matching process more powerful. The
algorithm of the matching can be selected before we
perform the loop. In a first loop, we could match the
cases with one particular algorithm and perform a
second loop with another algorithm. This can be
repeated until we are satisfied with the result or with
a pre-defined number of times. The result is a
matching flow which consists of several smaller
matching loops, running in parallel or sequential.
3 FUZZY MATCHING PROCESS
3.1 Introduction
The fuzzy case-based matching engine is capable of
comparing the properties of a set of cases and
produces a matching result indicating the degree to
which every two cases match. As mentioned earlier,
a case is any uniquely identifiable entity (a product
description, a buyer preference, a CV,…) containing
property values for certain criteria. For example,
criteria may be “color” and “price” and their
corresponding property values might be “red” and
“100$”, respectively.
In the remainder of this section, we describe the
internal workings of the engine in more detail.
Figure 2: The fuzzy matching engine’s internal
functionality
DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE
377
3.2 Input and internal data type
representation
Internally, the fuzzy engine performs its operations
using fuzzy data types. The property values of the
input cases may be defined in both a crisp (e.g. a
number or a range) or fuzzy (based on a membership
function) data type. Table 1 summarizes the
different data types that can be used in the fuzzy
engine.
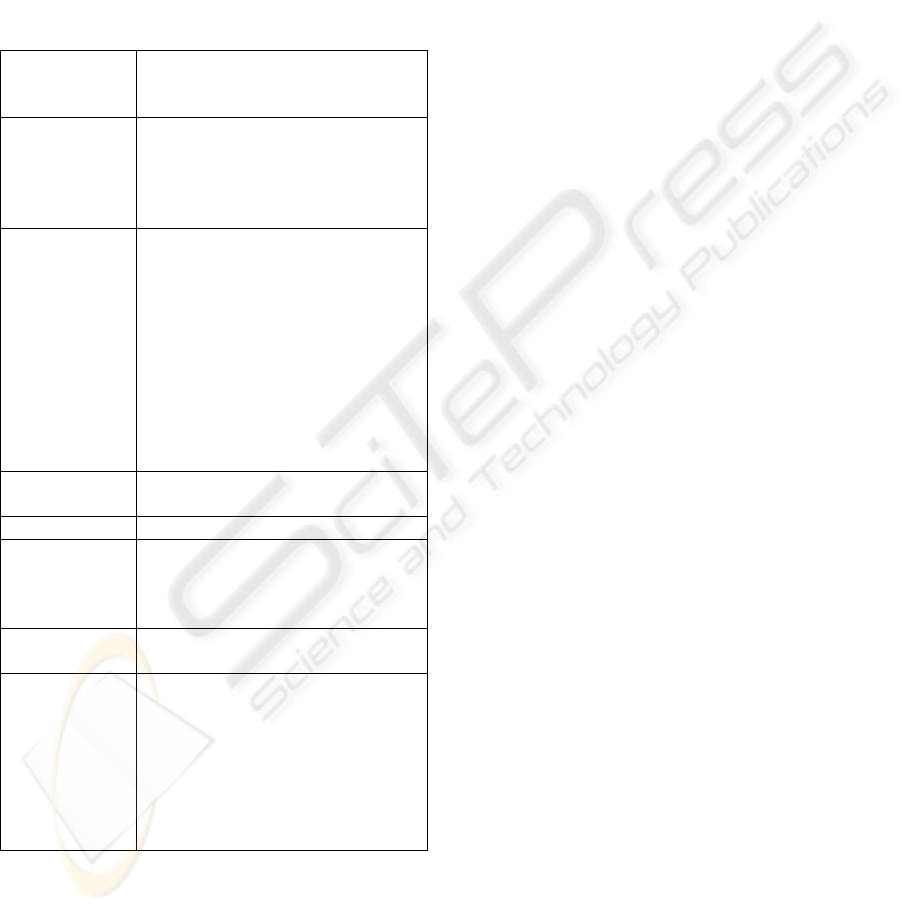
Table 1: Matching engine data types
Numerical A (crisp) number which can be
represented with double
precision
Discrete set A finite list of options. An option
can be any uniquely identifiable
object. An example of a discrete
set would be {“red”, “blue”,
“orange”}.
Weighted
Discrete Set
Identical to a standard discrete
set, however every set member
has an associated weight or
membership value (in the
interval [0,1]). This allows an
application to use fuzzy
modifiers for each et member,
each mapping to a certain
weight. For instance: 25%=“a
little”;50%=”somewhat”;
75%=”quite”,…
Range A single continuous numerical
range.
Range Set A unique set of ranges
Weighted
Range Set
A range set, with weights
associated to every range. This is
a generalization of a weighted
discrete set.
Fuzzy Set A fuzzy value, represented by a
function.
Case Properties may be compound.
For example a property “price”
may be a composition (linear
function) of “base price”, “VAT”
and “s&h”. These compound
properties are modeled as sub-
cases containing properties for
the sub-criteria.
Before comparing property values, the engine
converts any non-fuzzy property value into a fuzzy
value at the pre-processing phase. The matching
engine works with both point-functions and piece-
wise linear functions as membership functions for
fuzzy values. These can represent all the most
frequently used fuzzy set membership functions
(triangular, trapezoid…) and allow an approximation
of others, such as Gauss curves (De Baets et al.,
1989; Klir and Bo, 1995).
In order to match the properties of two distinct
cases, three standard operations need to be
performed: the fuzzification of the property values,
the aggregation of these fuzzy values, and the
defuzzification of the aggregation into a crisp
matching value, respectively (Xu et al., 2001). We
discuss each of these steps in the following sections
in some more detail.
3.3 Fuzzification
In order to convert crisp input values into fuzzy
values, a method of fuzzification needs to be
selected. A wide variety of fuzzification methods
exists, and the most suitable method for the case at
hand will depend on the usage context. Three
standard methods have been implemented in the
engine. In addition, specific fuzzification operations
can be performed in higher level applications,
simply by creating the appropriate function and
passing the result as a fuzzy property value to the
engine. The following fuzzification methods have
been implemented.
• Range-based fuzzification: This method
fuzzifies the value over a domain (UoD or
Universe of Discourse). The fuzzification factor
(a number in the interval [0,1]) indicates over
which percentage of the domain the value will
be fuzzified. The UoD width indicates how
wide the function domain is. The greater the
range, the wider the resulting fuzzy function
will be. In other words, this method assumes
that properties with a broader value domain
(e.g. “price” in interval [0-10.000]) need not be
matched as precise as properties with a narrow
domain (e.g. “age” in interval [25-65]). An
example: a numerical value is 1000 and the
domain is 0-2000. A triangular fuzzification
with fuzzification factor 0.1 will result in a
function with base x-coordinates 900-1100. The
same fuzzification over a domain 900-1100 will
result in a function with base 990-1010. This
ensures that the fuzzification is meaningful in
the specific UoD context.
• Fixed fuzzification: If no domain is available
however, the method for fixed fuzzification or
value-oriented fuzzification (presented next) can
be applied. The fixed fuzzification results in a
function with a specified base width, which
does not depend on the actual value. An
example: a numerical value is 1000 and the
fuzzification is 250. The resulting function will
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
378

have a base with x-coordinates 875-1125.
Clearly, this method of fuzzification should
only be used when no UoD is known, as the
fuzzification would be meaningless if the
domain is extremely wide (for example 0-
1.000.000) and exaggerated if the domain is
very narrow (for example 900-1100).
• Value-based fuzzification: This fuzzification
results in a function with a base width,
depending in the actual value. The greater the
value, the wider the base. An example: the value
is 100 and the fuzzification is 0.1. The resulting
function will have a base with x-coordinates 90-
110 (width=20). The same fuzzification on a
value of 1000 will result in a base 900-1100
(width=200). This fuzzification method is
therefore only applicable in certain contexts,
where larger values require less precise
matches.
Besides the fuzzification method, a fuzzifying
function needs to be defined. Depending on the
application context, this might for instance be a
triangular, trapezoid or Gauss function.
3.4 Aggregation
The second step is to aggregate the fuzzified values
in order to determine the degree to which these
values correspond. Three standard methods have
been implemented in the engine and, as was the case
for the fuzzification operations, additional
aggregation methods such as product or union can
be easily implemented by higher level applications.
The implemented methods are the following.
• Intersection: The intersection operator models
the fuzzy ‘AND’, and aggregates two fuzzy sets
using function intersection. Intersection is a
very strict yet commonly used form of
aggregation. Using fuzzy intersection, two
properties will only match well if they both
contain high membership values.
• Absolute difference: The absolute difference
aggregates two fuzzy sets into a function
representing the absolute difference of both.
The absolute difference between piecewise
linear functions is a new piecewise linear
function, and the absolute difference between a
point and a piecewise linear function is a new
point function. The difference aggregation does
not take into account the actual values of the
points, but only compares the amount in which
the both values differ. As a result, two very low
values might match much better than a low and
a high value. In certain contexts this might not
be the expected behavior and in these cases a
different aggregator should be used.
• Bounded difference: The bounded difference
determines the fuzzy difference between two
functions f
1
and f
2
, with a lower bound of 0. In
other words, the difference is max(f
1
-f
2
,0). In
contrast to the other aggregators, the order of
the functions is important here. Indeed, the
bounded difference of f
1
and f
2
is not
necessarily equal to the bounded difference of f
2
and f
1
. As with the absolute distance, this
aggregator is not suited for every form of
matching as a set of low preferences might
result in a perfect or near-perfect matching
score.
3.5 Defuzzification
The aggregation step is followed by a final step of
defuzzification a distance or matching value. This
resulting value is a measure for the similarity of two
property values. Depending on the data type of one
or both of the properties, either a numerical value or
range (partial matching) will be returned. As before,
additional operators can be easily added at the
Application layer, but the following operators are
available by default.
• Max: Simply returns the maximum membership
value of a fuzzy value. This can be used to
determine the maximum intersection value of
two properties and will be used most often in
fuzzy matching. However, if at least one of the
properties is a discrete set and the property
should only receive a high score if all of the
options in the set match well, average
intersection or a matching based on difference-
aggregation should be used. The max
defuzzification used in combination with a
bounded or absolute difference aggregation only
compares the similarity of property values,
without taking into account the actual values
themselves. This means, two properties with
both low, nearly equal values will score match
very closely. In some cases, this is not expected
behavior. In those cases distance function based
on intersection can be used.
• Average: Returns the average function value.
This property distance can be used when at least
one of the properties is a discrete set and the
property should only receive a high score if all
of the options in the set match well. If the
property score should reflect the score of the
best matching option, Max-Intersection should
be used instead.
DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE
379
0
20
40
60
80
100
120
140
160
180
200
1 10 100 1000
Crisp matching 1st run
Crisp matching 2nd run
Fuzzy matching 1st run
Fuzzy matching 2nd run
0
50
100
150
200
250
300
350
400
110100
Crisp matching 1st run
Crisp matching 2nd run
Fuzzy matching 1st run
Fuzzy matching 2nd run
.))0),()(max(1(
1
21
∑
−− xSxU
m
ii
C
j
C
.
|))()(|1(
1
,1
1
21
,1
1
2,1
∑
∑∑
=
=
−−
=
Ni
C
C
j
C
Ni
C
j
i
iii
W
xSxU
m
W
D
3.6 Matching
Once all property distances are computed for each of
the matching criteria, these distances can be turned
into a case distance. Several case distance functions
are available, however the weighted sum will be
used most frequently in fuzzy matching (Zadeh
1971).
Combining an intersection aggregator and a Max
defuzzification, will result in a matching value
defined as
with Ui and Si property values for a criterion Ci and
Wi a weight for the criterion Ci. Combining an
absolute difference aggregator and an Avg
defuzzification, will result in
The bounded difference and Avg defuzzification
amount to (unweighted):
4 FUZZY MATCHING ENGINE
SCALABILITY TESTING
This section provides a brief overview of the
performance of the fuzzy case-based matching
engine.
The benchmarks were performed under the
following test conditions: Hardware: P4-2,66Ghz,
512Mb Ram; Software: Windows XP, JDK1.4.1
Configuration: Single threaded; Fuzzy config: Fixed
value fuzzification (other fuzzification types are
marginally slower). All times are represented in
milliseconds (ms). Two runs are performed per
evaluation, to ensure initialization and configuration
of the matching engine are not taken into account.
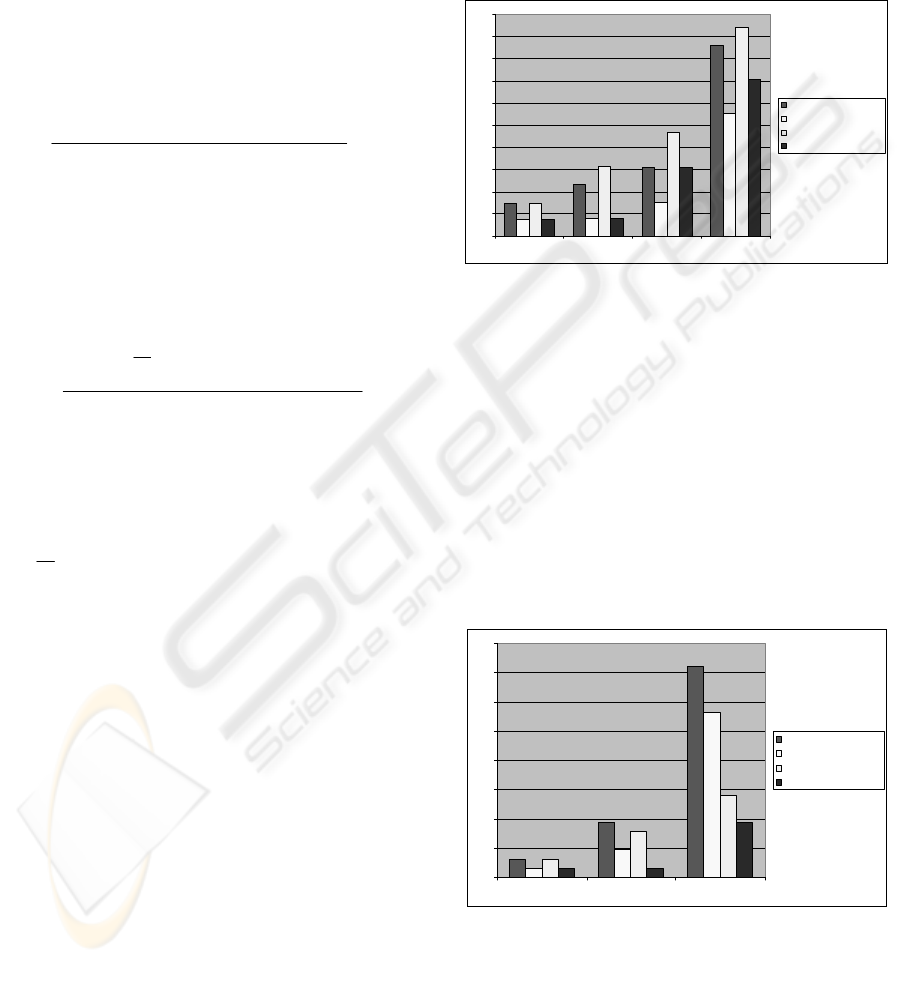
4.1 Case scaling
This test benchmarks matching speed for cases with
a single property, in order to evaluate the scaling in
function of the amount of cases. 1000 cases are
evaluated in approximately 140 ms when fuzzy logic
is used.
Using a plain CBR algorithm, 1000 cases are
evaluated in approximately 110 ms. The chart also
illustrates that the engine scales in a logarithmic and
not a linear fashion. This means the engine works
optimally when processing a large amount of cases.
4.2 Property scaling
This test benchmarks matching speed for a single
case, with an increasing amount of properties.
Here we note that the fuzzy algorithm
implementation is faster than standard CBR when
,
)))(),(((
,1
1
21
,1
1
2,1
∑
∑
=
=
=
Ni
C
C
j
C
Ni
C
j
i
iii
W
xSxUMinMaxW
D
Figure 3: Results of the case scaling tests for the fuzzy
matching engine
Figure 4: Results of the property scaling test for the
fuzzy matching engine
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
380
0
100
200
300
400
500
600
700
10 100 1000
Crisp matching 1st run
Crisp matching 2nd run
Fuzzy matching 1st run
Fuzzy matching 2nd run
0
100
200
300
400
500
600
700
800
900
10 100 1000
Fuzzy matching 1st run
Fuzzy matching 2nd run
processing a limit amount of cases with a large
amount of properties.
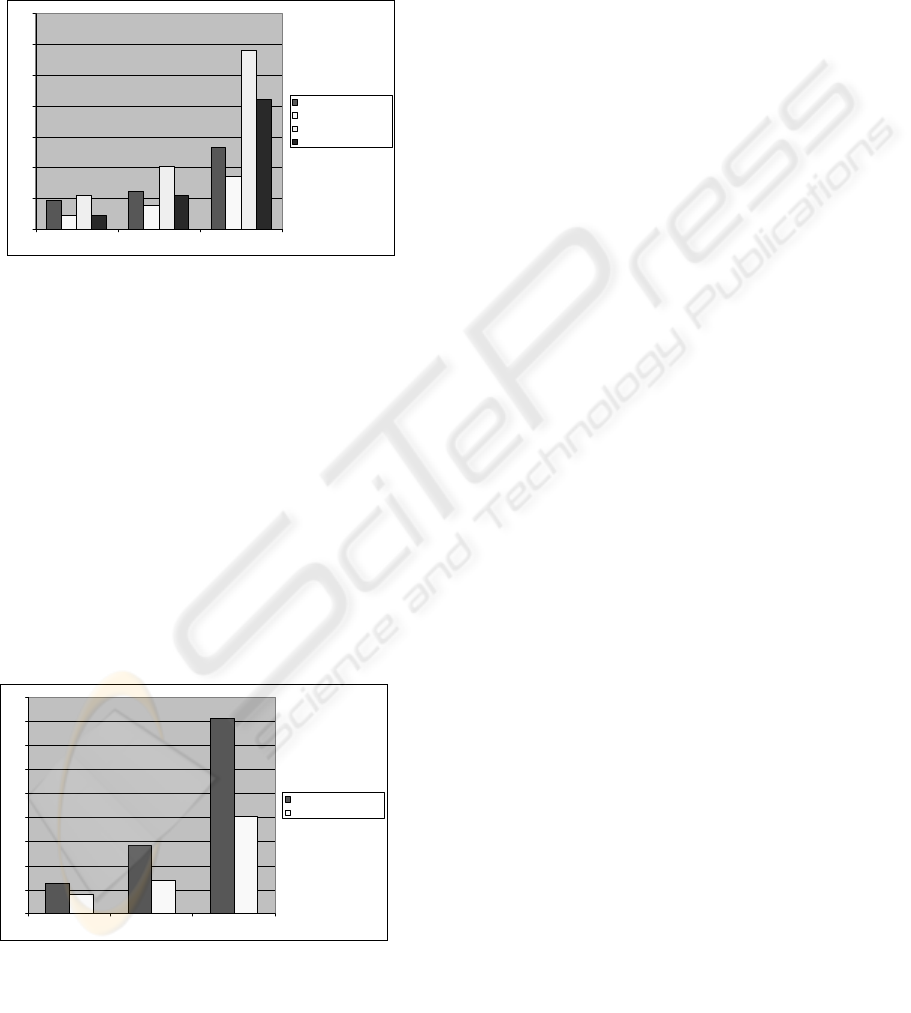
4.3 Real-world scaling
This benchmark tests matching speed for an
increasing amount of cases, with 10 properties each.
Most cases in real world applications can be
represented with no more than 10 properties, so that
this test gives a good idea of real world
performance. 1000 cases can be ‘fuzzy’ matched
against each other in approx. 400 ms (180 ms for
standard CBR). This means the matching engine is
capable of performing 25,000 fuzzy matches per
second, which is faster than most databases can
produce the data required for the matching.
4.4 Fuzzy scaling
All previous benchmarks were performed on pure
numerical properties. This benchmark tests the fuzzy
matching speed for an increasing amount of cases.
Each case contains 7 properties, of which 2 are
compound and nested within each other. Properties
are created randomly and are of types numeric,
interval, discrete weighted set, range set and fuzzy.
Matching 1000 cases takes approximately 400 ms.
5 CONCLUSIONS AND FUTURE
WORK
We have presented design and implementation
issues that have influenced and defined the
development of a fuzzy case-based matching engine.
We stressed the flexibility of the engine, which is
reflected in the variety of case data types on the one
hand and fuzzy set theoretical matching operations
on the other hand. We have analyzed the scalability
of the engine, and found that the engine is capable of
dealing with complex cases under increasing load
conditions. The applicability of the matching engine
is currently being investigated for e-marketplaces for
student jobs (Kurbel et al., 2001; Hansenne et al.,
2003; Van de Walle 2003(b); Hansenne et al., 2004)
and negotiation processes in electronic markets
involving complex multi-issue cases (Van de Walle
et al., 2001). We have recently developed a
theoretical model to deal with incomplete case
information and asymmetric matching processes
(Van de Walle and Van der Sluys, 2002; Van de
Walle 2003(a)), and our near term research objective
is to implement that model in the engine’s
application layer and investigate its applicability for
real world electronic markets.
REFERENCES
Aamodt, A. and E. Plaza, 1994. Case-Based Reasoning:
Foundational Issues, Methodological Variations, and
System Approaches. In AICom - Artificial Intelligence
Communications, IOS Press 7 (1), 39 – 59.
De Baets, B., M.M. Gupta and E.E. Kerre, 1989. Expert
knowledge representation by means of piecewise linear
fuzzy quantities. In Proceedings of the Third
International Fuzzy Systems Association Congress 89
(Seattle, WA, USA), 618-621.
Hansenne, R., V. Van der Sluys and B. Van de Walle,
2003. Smart Web Services in Action: Student Odd
Jobs on University Websites. In Proceedings of the
International Conference on Information Technology:
Research and Education ITRE2003 (Newark, New
Jersey USA), 255 – 256.
Hansenne, R., V. Van der Sluys and B. Van de Walle,
2004. Implementation of a web services based
recruitment platform. Submitted to WSMAI-2004, The
2
nd
International Workshop on Web Services –
Figure 5: Results of the real-world scaling tests for
the fuzzy matching engine
Figure 6: Results of the fuzzy scaling tests for the
fuzzy matching engine
DESIGN AND IMPLEMENTATION OF A SCALABLE FUZZY CASE-BASED MATCHING ENGINE
381

Modeling, Architecture and Infrastructure (Porto,
Portugal).
Klir, G. and Y. Bo, 1995. Fuzzy Sets and Fuzzy Logic:
theory and Applications. Prentice Hall, Englewood
Cliffs, NJ.
Kolodner, J., 1993. Case Based Reasoning. Morgan
Kaufmann Press.
Kurbel, K.; Loutchko I.; Klaue S.: Automated Negotiation
on Agent-Based E-Marketplaces: An Overview; in:
O'Keefe, B. et al. (Eds.): Proceedings of 14th Bled
Electronic Commerce Conference; Bled, Slovenia;
June 2001, pp. 508-519.
Pal, S., T. Dillon, and D. Yeung, (Eds.), 2001. Soft
Computing in Case Based Reasoning. London, U.K.:
Springer-Verlag.
Van de Walle, B., S. Heitsch and P. Faratin, 2001. Coping
with One-to-many Multi-criteria Negotiations in an
Electronic Marketplace. In Proceedings of the e-
negotiatons Workshop at the 17
th
International
Database and Expert Systems Applications Conference
DEXIA’01 (Munchen, Germany), 747 –751.
Van de Walle, B. and V. Van der Sluys, 2002. Non-
symmetric Matching Information for Negotiation
Support in Electronic Markets. In Proceeding of the
International Workshop on Information Systems
EuroFuse2002 (Trento, Italy), 271 – 276.
Van de Walle, B., 2003(a). A relational analysis of
decision makers’ preferences. In International Journal
of Intelligent Systems 18, 775 – 791.
Van de Walle, B., 2003(b). Relational structures for the
analysis of decision information in electronic markets.
In Applied Decision Support with Soft Computing
(Eds. X. Yu and J. Kacprzyck), Studies in Fuzziness
and Soft Computing Series Vol. 124, Springer-Verlag,
pp. 196 – 217.
Watson, I.D., 1997. Applying Case-Based Reasoning:
Techniques for Enterprise Systems. Morgan Kaufman
Publishers.
Xu, Y., E.E. Kerre, D. Ruan and Z. Song, 2001. Fuzzy
reasoning based on the extension principle. In
International Journal of Intelligent Systems 16, 469 –
495.
Zadeh, L.A., 1971. Similarity relation and fuzzy orderings.
In Information Sciences 3, 177 – 200.
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
382
