Descovering Collocations in Modern Greek Language

Kostas Fragos

, Yannis Maistros

, Christos Skourlas

1 Department of Computer Engineering, National Technical University of Athens,

Iroon Polytexneiou 9 15780 Zografou Athens Greece

2 Department of

Computer Engineering, National Technical University of Athens,

Iroon Polytexneiou 9 15780 Zografou Athens Greece

3 Departme

nt of Computer Science, Technical Educational Institute of Athens,

Ag Spyridonos 12210 Aigaleo Athens Greece

Abs

tract. In this paper two statistical methods for extracting collocations from

text corpora written in Modern Greek are described, the mean and variance

method and a method based on the X

test. The mean and variance method

calculates distances (“offsets”) between words in a corpus and looks for specific

patterns of distance. The X

test is combined with the formulation of a null

hypothesis H

for a sample of occurrences and we check if there are

associations between the words. The X

testing does not assume that the words

in the corpus have normally distributed probabilities and hence it seems to be

more flexible. The two methods extract interesting collocations that are useful

in various applications e.g. computational lexicography, language generation

and machine translation.

1 Introduction

Collocations are common in Natural Languages and can be found in technical and

non-technical texts. A collocation could be seen as a combination of words (or

phrases) which are frequently used together. Collocations in Natural Languages with

rich inflectional system (e.g. Modern Greek) could also be seen as phrases where the

occurrences of nouns follow a “rigid” syntactic / grammatical form e.g. the Greek

words “Χρηµατιστήριο” and “Αξιών” are only combined in the collocation

“Χρηµατιστήριο Αξιών” (Stock Exchange). Other words / phrases are more “flexible”

e.g. the Greek words “Στρώνω / στρωνοµαι” and “δουλειά” could be combined in

various phrases having different meaning, as the following ones:

“Στρώνοµαι στην δουλειά” (To get to work)

“Η δουλειά µου στρώνει” (My business is looking up).

There are different definitions based on different aspects of collocations. Firth [6]

defines Collocations of a given word as “statements of the habitual or customary

places of the word”.

Fragos K., Maistros Y. and Skourlas C. (2004).

Descovering Collocations in Modern Greek Language.

In Proceedings of the 1st International Workshop on Natural Language Understanding and Cognitive Science, pages 151-158

DOI: 10.5220/0002667101510158

 SciTePress

Benson and Morton [1] define collocations as an arbitrary and recurrent word

combination. The word recurrent means that these combinations are common in a

given context. Smadja [15] identifies four characteristics of collocations useful for

machine applications:

a) Collocations are arbitrary; this means that they do not correspond to any syntactic

or semantic variation. b) Collocations are domain-dependent; hence handling text in a

domain requires knowledge of the related terminology / terms and the domain-

dependent collocations. c) Collocations are recurrent (see above) d) Collocations are

cohesive lexical clusters; by cohesive lexical clusters is meant that the presence of one

or several words often implies or suggests the rest of the collocation.

In the work of Lin [10] collocation is defined as a habitual word combination. Gitsaki

et. al. [7] define it as a recurrent word combination. Howarth and Nesi [8] have

approached the use of collocations from the foreign language learner perspective.

Manning and Schutze [11] believe that collocations are characterized by limited

compositionality. A natural language expression is compositional if the meaning of

the expression can be predicted from the meaning of the parts. Hence, collocations are

not fully compositional. For example in the Greek expression “γερό ποτήρι” (heavy

drinker), the combination has an extra meaning, a person who drinks. It is completely

different from the meaning of the two “collocates” (portions of the collocation):

“γερό” (strong), “ποτήρι” (glass). Another characteristic of collocations is the lack of

valid synonyms for any collocates [11], [10]. For example, even though baggage and

luggage are synonyms we could only write emotional, historical or psychological

baggage.

2 The Rationale for Extracting Collocations in NLP Applications

Collocations are important in Natural Language generation, machine translation

[7],[8], text simplification [2], computational lexicography [14] etc. Smith [16]

examined collocations to detect events related to place and date information in

unstructured text.

In this paper we describe two statistical methods for extracting collocations from text

corpora written in Modern Greek. The first one is the mean and variance method that

calculates “offsets” (distances) between words in a corpus and looks for patterns of

distances. The second method is based on the X

test. In section 3 we focus on the

main ideas of applying the two methods. Some previous work in the field is also

discussed. Then, in section 4, the two methods are described. A short presentation of

the test data used and some experimental results are given in section 5. Discussion

and further work are given in section 6.

3 How to Extract Collocations Using Statistical Methods

The “traditional” approach for extracting collocations has been the lexicographic

one. Benson and Morton [1] propose that collocates, the “participants” in a

collocation, could not be handled separately. Therefore the task of extracting the

152

appropriate collocates is not predictable, in general, and collocations must be

extracted, manually, and listed in dictionaries.

In recent years, statistical approaches have been applied to the study of natural

languages and the extraction of collocations. Such approaches were partially

influenced by the availability of large corpora in machine-readable form. Choueka [3]

tried to automatically extract collocations from text, using N-grams from 2 to 6

words.

A simple method for extracting collocations based on a corpus is the frequency of

occurrence. If two or more words often appear together then we have an evidence for

the existence of collocation. Unfortunately, the selection of the most frequently

occuring N-grams does not always lead to interesting results. For example, if we look

for bigrams in a corpus the resulting list will consist of phrases such as: of the, in the,

to the, etc. To overcome this problem Justeson and Katz [9] proposed a heuristic

improving the previous results. They use a part-of-speech filter for the candidate

phrases and select only those N-grams that follow specific patterns. Some patterns

used for collocation filtering (in their heuristics) are AN, NN, AAN and ANN, where A

stands for adjective, N for noun. Although the heuristics are very simple the authors

reported significant results.

The method based on the frequency of occurrences works well for noun phrases.

However, many collocations involve words having other more flexible relationships.

The mean and variance method [15] overcomes this problem by calculating the

distance between two collocates and finding the “spread” of the distribution. The

method calculates the mean and variance of the “offset” (“signed” distance) between

the two words in the corpus. Such a method makes sense, intuitively. If the “spread”

of the distribution is low we have a narrow peaked distribution of “offsets” and this is

an evidence of the existence of a collocation. On the other hand, if the variance is

high the “offsets” are randomly distributed, i.e., there is no evidence of the existence

of a collocation.

"Mutual information" is a measure for extracting collocations [4]. The term

"mutual information" originates from information theory. The term "information" has

the restricted meaning of an event, which occurs in inverse proportion to its

probability. Church and Hanks [4] define "mutual information” as “holding between

the values of random variables”. It is roughly a measure of how much one word “tell

us” about the other.

We will describe the main ideas of applying the two statistical methods, the mean

and variance method and the X

test (pronounced ‘chi-square test’). We shall also

give an alternative formula for the calculation of X

statistic in the case of extracting

bigrams based on a corpus. The X

test is a well-defined approach in statistics for

assessing whether or not something is a chance event. This is, in general, one of the

classical problems of statistics and it is usually formulated in terms of hypothesis

testing. In our study, we want to know whether two words “occur” together more

often by chance. We formulate a null hypothesis H

for a sample of occurrences. The

hypothesis states that there is no association between the words beyond chance

occurrences. We calculate the probability p that the event would occur if H

were true.

If p is too low (under a predetermined significance level p<0.005 or 0.001) we reject

the H

(or retain H

, otherwise). To determine these probabilities usually we calculate

the t statistic:

153

(1)

where

is the sample mean, s

is the sample variance, N the size of the sample and µ

is the mean of the distribution if the null hypothesis were true.

If the t statistic is large enough we can reject the null hypothesis. The problem with

the t statistic is that it assumes normally distributed data. This assumption is not true,

in general, for linguistic data. For this reason we choose the X

test, which does not

assume normally distributed data. However, for this statistics, various side effects

have been observed with sparse data. Dunning [5] proposed an alternative testing the

likelihood ratios that works better than X

with sparse data.

4 Methods for Discovering Collocations

4.1 Mean and Variance

The mean is the simple arithmetic average value of the data. If we have n

observations x

, x

,, … x

, then the mean is given by the form:

(2)

The variance of the n observations x

, x

,, … x

is the average squared deviation of

these observations about their mean:

(3)

The standard deviation s is the square root of the variance.

(4)

4.2 Pearson’s chi-square test

In 1900, Karl Pearson developed a statistic that compares all the observed and

expected numbers when the possible outcomes are divided into mutually exclusive

categories. The form in equation 5 gives the chi-square statistic:

(5)

154

where the Greek letter Σ stands for summation and is calculated over the categories of

possible outcomes.

The observed and expected values can be explained in the context of hypothesis

testing. If we have data that is divided into mutual exclusive categories and form a

null hypothesis about that data, then the expected value is the value of each category

if the null hypothesis is true. The observed value is the value for each category that

we observe from the sample data.

The chi-square test is a remarkably versatile way of gauging the significance of

how closely the data agree with the detailed implications of a null hypothesis.

5 Experimental results

Several files of Greek language texts were collected and a preliminary part-of-

speech tagging process had been done to form a linguistic Corpus of 8,967,432

lemmas (or 29,539,802 words). This corpus will be a useful resource for future works.

We were interested only for the lemmas where the part-of-speech tag is Noun (No),

Verb (Vb), Adjective (Aj) and Adverb (Ad). These lemmas are distributed as follows:

Nouns=6,739,006 , Verbs=0 , Adjectives=2,228,426 , Adverbs=0.

Note that lemmas for Verbs and Adverbs are not provided. The remaining 8,977,083-

8,967,432=9,651 lemmas belong to a category tagged as RgFwGr and are related to

foreign words used in Greek Language.

5.1 Analysis of Variance

The only combination of bigrams we have tried is that of pairs (Adjective, Noun).

We calculate from the corpus the distances and the standard deviation of these

distances, for all the combinations of bigrams (Adjective, Noun), defining a

collocational window of 10 words (including punctuation marks). By a positive

distance d ( | d | <=10) we mean that the noun is found in a distance of d words on

the right hand side of the adjective. A negative distance denotes that the noun is found

in a distance of d words in the opposite side. Table 1 shows the 10 lowest standard

deviation bigrams.

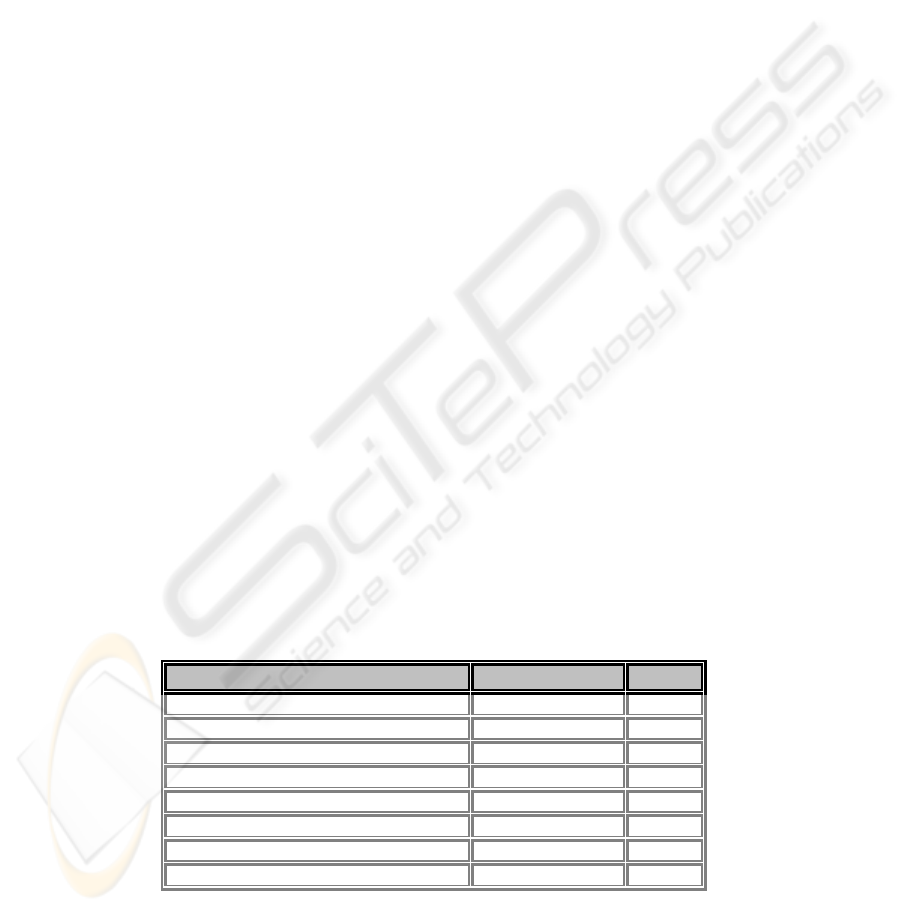
Table 1. The 10 lowest standard deviation bigrams in the corpus

Lemma_adj Lemma_nou stdv

"χρονικό" "διάστηµα" 0,7654

"κεντρική" "σηµασία" 0,8321

"ειδικός" "απάντηση" 1,1875

"µεγάλος" "βαθµός" 1,1932

"περασµένος" "κανόνας" 1,3007

"αµερικανική-αµερικανικής" "κανόνας" 1,3817

"κυριακής" "ελλάδα" 1,3901

"ανά" "κόσµος" 1,4151

155

Lemma_adj Lemma_nou stdv

"οικονοµικό" "παιχνίδι" 1,4434

"εργαζοµένα-εργαζοµένη-εργαζοµένης" "διεθνός-διεθνώς" 1,4546

Interpretation: For a bigram with a low standard deviation of the distances between

the words the existence of a half-sided high peak value distribution is a strong

indication that these words form a collocation. In other words, the narrow shape and

the high peak value of the distribution offer a strong indication that these words form

a collocation.

5.2 Analysis of X-square test

The X-square test is more flexible than the method of the variance, which can be

disastrous in the cases of extremely high frequencies. The X

statistic makes a

hypothesis (the null hypothesis) of statistical independence for the two words of a

bigram. That is, the null hypothesis supposes that the two words occur independently

of each other within the corpus. Calculating the X

statistic we can reject the null

hypothesis if it exceeds a critical value as defined from the X distribution

Experimental results. Our corpus consists of 29,539,802 words. Using this number

and a collocational window of 10 words around a target adjective we can calculate the

total number of bigrams (adjective, noun). Hence, the total number can be calculated

by the form Total_number_of_bigrams = (29,539,802-9)*9+36.

For each one of these bigrams we scan the corpus and calculate the

entries of

the 2-by-2 contingency table to evaluate eventually the X

score. Table 2 shows the 10

highest X

score

Table 2. The 10 highest X–square score bigrams in the corpus

Adjective Noun X2score

a12 a21 a22

"κοινωνικής" "διάλογος" 3,4057 59 117373 41737 265699004

"κοινωνικής" "µείωση" 3,3964 10 112994 41786 265703383

"διαφορετικός" "µέλη" 3,3488 11 116863 43135 265698164

"συγκεκριµένος" "σηµασία" 3,3426 11 111553 45637 265700972

"χρονικό" "δηµόσια" 3,3325 9 112041 41553 265704570

"προοπτική "µείωση" 3,2941 11 112993 45169 265700000

"ίδιο" "παρουσία" 3,1651 11 112471 44161 265701530

"διαφορετικός" "συµφωνία" 3,1563 11 115063 43135 265699964

"σηµερινή" "συµφωνία" 3,1501 10 115064 42776 265700323

"κυπριακός" "σηµασία" 3,1498 12 111552 47454 265699155

156

6 Discussion and further work

This work presents two methods of automatic extraction of collocations in the case

of the Greek language: The “mean and variance” method and the X

testing. In the

case of the X

testing, we have demonstrated that it is possible to work effectively

with large corpora of the Greek Language.

We could use various other statistical methods for calculating significance, like

mutual information (MI), log likelihood (LL) ratio test, t-test etc., but we choose to

use the chi-square statistics. The reason is that the other tests assume a parametric

distribution of the data. This is unsuitable when calculating frequencies of bigrams.

Likelihood ratio seems to work better than X

, when we have sparse data.

MI compares the joint probability p(w

) that two words occur together with the

independent probabilities p(w

), p(w

) that the two words occur in the data. The form

MI(w

, w

) = log

( p(w

) / p(w

)* p(w

) ) does not give us interesting results for

very low frequencies.

The X

testing is the most commonly used test of statistical significance in

computational linguistics and can be used in many different contexts.

In the future, our study can incorporate lexical knowledge to assist in extracting

collocations and improve the results. Such knowledge can be based on the use of

lexical thesaurus, synonymy, hypernymy and part of speech tagging available for the

Greek language. Pearsen [13] has worked in a similar way using WordNet Lexicon

[12] for the English language. Using such statistical methods we might have an

effective representation of the knowledge. By combining statistical methods in a

conceptual graph knowledge representation framework, we could collect valuable

information and obtain rich knowledge bases. In general, combining statistical

methods and Computer assessment of knowledge structure seems to be an interesting

and promising next step.

7 References

1. Benson & Morton 1989. The structure of the collocational dictionary. In International

Journal of Lexicography 2:1-14.

2. Caroll J., Minnen G., Pearse D., Canning Y., Delvin S. and Tait J. (1999). Simplifying

text for language-impaired readers. In Preceedings of the 9th Conference of the European

Chapter of the ACL (EACL '99), Bergen, Norway, June.

3. Choueka, Y.; Klein, T.; and Neuwitz, E. (1983). "Automatic retrieval of frequent

idiomatic and collocational expressions in a large corpus." Journal for Literary and Linguistic

Computing, 4, 34-38. In Information Theory, 36(2), 372-380. Fano, R. (1961). Transmission of

Information: A Statistical Theory of Information. MIT Press. Flexner, S., ed. (1987). The

Random House.

4. Church, K., and Hanks, P. (1989). "Word association norms, mutual information, and

lexicography." In Proceedings, 27th Meeting of the ACL, 76--83. Also in Computational

Linguistics, 16(1). algorithm." IEEE Transactions on Information Theory, IT-26(1), 15-25.

HaUiday, M. A. K., and Hasan, R. (1976). Cohesion in English. Longman.

5. Dunning, T. (1993). Accurate Methods for the Statistics of Surprise and Coincidence.

Computational Linguistics, Volume 19, number 1, pp61-74.

157

6. Firth J. R. (1957). A synopsis of linguistic theory 1930-1955. In Studies in Linguistic

Analysis, pp 1-32. Oxford: Philological society. Reprinted in F. R. Palmer(ed), Selected papers

of J. R. Firth 1952-1959, London: Longman, 1968.

7. Gitsaki C., Daigaku N. and Taylor R. (2000). English collocations and their place in the

EFL,classroom available at: http//www.hum.nagoya-

cu.ac.jp/~taylor/publications/collocations.html.

8. Howarth P. and Nesi H. (1996). The teaching of collocations in EAP. Technical report

University of Leeds, June.

9. Juteson S. and Katz S. (1995b). Technical terminology: some linguistic properties and an

algorithm for identification in text. Natural Languagr Engineering 1:9-27.

10. Lin D. (1998). Extracting collocations from text corpora. In First Workshop on

Computational Terminology, Montreal, Canada, Augaust.

11. Manning C. and Schutze H.(1999). Foundations of Statistical Natural Language Processing

(Fifth Printing 2002). The MIT Press.

12. Miller G., Beckwith R., Fellbaum C., Gross D. and Miller K. (1993). Introduction to

WordNet: An On-line Lexical Database. Five Papers on WordNet Princeton University.

13. Pearce D. (2001). Synonymy in Collocation Extraction. . In WordNet and Other Lexical

Resources: Applications, Extensions and Customizations (NAACL 2001 Workshop). pages 41-

46. June. 2001. Carnegie Mellon University, Pittsburgh.

14. Richardson, S. D. (1997). Determining similarity and inferring relations in a lexical

knowledge base [Diss], New York, NY: The City University of New York.

15. Smandja F. (1993). Retrieving collocations from text: Xtract. Computational Linguistics,

19(1):143-177, March.

16. Smith A. David (2002). Searching across language, time, and space: Detecting events with

date and place information in unstructured text July 2002 In Proceedings of the second

ACM/IEEE-CS joint conference on Digital libraries

158