Reasoning about the Properties of an Enterprise

Information System

John A. van der Poll

and Paula Kotz

School of Computing

University of South Africa

Abstract. A condensed speciﬁcation of a multi-level marketing enterprise in the

Z speciﬁcation language is presented and a number of proof obligations that result

from operations on the state is stated. The feasibility of using certain reasoning

heuristics for discharging proof obligations emerging from the speciﬁcation is

investigated and we show how two important proof obligations arising from the

speciﬁcation of a real-life enterprise may successfully be discharged using a suite

of well-chosen heuristics.

1 Introduction

Among the beneﬁts to be gained by using a formal speciﬁcation language like Z [1] is

that the speciﬁer can prove things about the speciﬁcation. The process of constructing

proofs can aid in the understanding of the system and may reveal hidden assumptions

[2].

The huge cost and inconvenience of detecting and correcting errors only after the

system has been released [3], justiﬁes the effort to identify and correct errors at an

early stage (e.g. speciﬁcation phase). However, the readiness with which the informa-

tion technology industry would accept such a methodology is likely to depend on the

availability of environments that ease the burden on the speciﬁer by automating much

of the speciﬁer’s tasks. The more sophisticated the environment (and thus the greater its

contribution to the partnership), the more natural becomes the inclusion of a reasoning

algorithm as one component.

Reasoning about the properties of an enterprise information system at the speciﬁ-

cation level may, however, be a non-trivial task owing to the size of the system or the

complexity of the structures that make up such a system. Accounts of costly, yet failed

proof attempts exist. Mokkedem et al. [4] report that an attempt to generate a proof

monolithically in one step from a stated property to a protocol was prohibitively difﬁ-

cult. The one step proof was abandoned, unﬁnished, after 18 months of effort which led

to the speciﬁers eventually adopting an incremental proof strategy.

Since Z is based on ﬁrst-order logic and a strongly typed fragment of Zermelo-

Fraenkel (ZF) set theory, it makes sense to investigate to what extent a set of heuristics

[5] for proving theorems in set theory may be used to reason about the Z speciﬁcation

of a multi-level marketing enterprise.

A. van der Poll J. and Kotzé P. (2004).

Reasoning about the Properties of an Enterprise Information System.

In Proceedings of the 2nd International Workshop on Veriﬁcation and Validation of Enterprise Information Systems, pages 10-19

DOI: 10.5220/0002672000100019

 SciTePress

1.1 Why Reasoning Heuristics?

Traditionally set-theoretic proofs pose demanding challenges to automated reasoning

programs [6, ?], since unlike number theory or group theory or applications to real

systems such as power stations, the denotations of terms in the context of set theory are

strongly hierarchical: one object (perhaps at a very ﬁne level of granularity) is a member

of another (coarser) object, which in turn may be a member of a higher-level (even

coarser) object, and so on. The possibility of moving between levels is a provocation

to much irrelevant activity; intelligence would be realised by heuristics that limit the

movement up or down to productive changes of granularity [7].

It is furthermore an open problem as to which inference rule would build set the-

ory into a theorem prover the same way as paramodulation builds in equality-oriented

reasoning [8]. Paramodulation is a rule applied to a pair of clauses and requiring that at

least one of the two contains a positive equality literal, and yielding a clause in which

an equality substitution corresponding to the equality literal has occurred. The object of

an application of paramodulation is, therefore, to cause an equality substitution to take

place from one clause into another.

Devising a set of heuristics appears to be the best strategy for reasoning about set-

theoretic constructs [7]. Such a set of heuristics was developed by one of the authors [5]

and in this paper we investigate to what extent these heuristics are useful for reasoning

about the properties of a franchise or a multi-level marketing enterprise [9].

1.2 Structure of this Paper

Section 2 presents a brief overview of OTTER [10], the automated reasoner used in this

work. A number of heuristics for reasoning about set-theoretic structures is presented

in Sect. 3. A brief Z speciﬁcation of a generic multi-level marketing enterprise [9] is

given in Sect. 4. Some applications of the said heuristics are illustrated in Sect. 5 where

two proof obligations (POs) are stated and discharged using an automated reasoner. A

summary and some ideas about future work conclude this paper.

2 The OTTER Theorem Prover

OTTER (Organized Techniques for Theorem Proving and Effective Research) [10] is

a resolution-based theorem-proving program for ﬁrst-order logic with equality and in-

cludes the inference rules binary resolution, hyperresolution (both positive and nega-

tive versions), UR-resolution and binary paramodulation. OTTER was written and is

distributed by William McCune at the Argonne National Laboratory in Illinois.

OTTER can convert ﬁrst-order formulae into sets of clauses, which constitute the

input to the resolution algorithm. Of course, OTTER cannot accept formulae in the

highly evolved notation of set theory so the user has to rewrite set-theoretic formulae

in terms of a weaker ﬁrst-order language having the relevant relations and functions

as predicate symbols and function symbols in its alphabet. Some other capabilities of

At the time of writing the latest version of OTTER is available at: http://www-

unix.mcs.anl.gov/AR/otter.

OTTER are factoring and weighting. The purpose of a weight clause is give a weight to

variables or terms and if such weight is chosen sufﬁciently high then the generation of

too many irrelevant paramodulants is effectively blocked. Note, however, that the use

of a weight leads to an incomplete search strategy.

An OTTER program is divided into several sections, each such section made up

of ﬁrst-order formulae or clauses (an exception is the section containing the optional

demodulators which must be in clausal form already). The most important sections are

the usable list and the set-of-support (sos) list. It is customary to place the negation of

the theorem to be proven in the sos and the rest of the information in the usable list.

Next we introduce a number of heuristics for reasoning about set theory. These

heuristics were developed to address the problems discussed in Sect. 1.1.

3 Set-Theoretic Reasoning Heuristics

The heuristics presented in this section are detailed in [5, ?] and have been developed

empirically through observing the behaviour of, as well as studying the format of the

clauses generated by the reasoner during a proof attempt. In total 14 heuristics were

developed and we brieﬂy discuss some prominent ones below:

1. Weight strategy: Use the setting weight(x,n), for n ∈ {3, 4, 5}, whenever the

sos consists of the negation of an equality literal. Equality reasoning with paramod-

ulation generally results in the generation of many irrelevant clauses. Assigning a

weight of n to all variables avoids the generation of too many irrelevant paramod-

ulants. Empirically we found a weight of 3, 4 or 5 to be sufﬁcient.

2. Extensionality: Use the principle of extensionality to replace an equality in the sos

with the condition under which two sets are equal, i.e. whenever their elements are

the same.

3. Nested functors: Avoid, if possible, the use of nested functor symbols in deﬁnitions.

Terms built up with the aid of function symbols (called functors) are more complex,

potentially leading to difﬁculties with uniﬁcation of terms, especially when these

functors are nested inside other structures.

4. Divide and Conquer: Perform two separate subset proofs whenever the problem at

hand requires one to prove the equality of two sets. An equality in the sos implies

(via Extensionality) an ‘if and only if’. Hence a speciﬁer may opt for two proofs,

one for the only-if part and another for the if part.

5. Multivariate functors: Make terms in sets as simple as possible — either not in-

volving functors at all, or else involving functors with the minimum number of

argument positions taken up by variables. The more variables occur as arguments

to a functor, the greater the likelihood of thrashing caused by the uniﬁcation of

these variables with other terms.

6. Intermediate structures: Avoid complex functor expressions by using an indirect

deﬁnition for an internal structure whenever this appears less likely to produce

complex functor expressions than the direct deﬁnition. In practice we simply give a

name to a complex structure that is nested inside another structure and then deﬁne

the inner structure externally on its own, instead of unfolding its deﬁnition directly

inside the enclosing structure.

7. Element structure: Deﬁne the elements of relations and functions directly in terms

of ordered pairs or ordered n-tuples whenever the tuples need to be opened to ﬁnd

a proof. An ordered n-tuple is an example of a functor and projecting out the coor-

dinates of the tuple often avoids the various functor problems listed above.

8. Search-guiding: Generate and use half deﬁnitions, via the technique of resolution

by inspection, for biconditional formulae in the usable list whenever the sos con-

sists of a conditional formula or a single literal. A half deﬁnition is an implication

(e.g. only-if) as opposed to an if and only if deﬁnition. Through inspection it is

often possible to trace the initial steps a reasoner would perform starting with the

conditional formula in the sos. Hence it is possible to predict which half of some

deﬁnitions in the usable list would probably be needed and which ‘other halves’ are

redundant.

9. Inference rule selection: Use set(neg

hyper

res) in the place of positive hy-

perresolution whenever the combined use of set(hyper

res) and set(ur

res)

rapidly makes the sos empty. If no rapid proof results, try binary resolution. Both

forms of hyperresolution are capable of generating homogeneous clauses only (i.e.

just positive or just negative but not mixed). Although many researches warn against

the use of binary resolution [11] we found such rule to be occasionally useful (see

Sect. 5 below).

10. Resonance: Attempt to give corresponding terms in formulae a syntactically similar

structure to aid the resolution process [12]. Not only does this apply to terms just in

the usable list, but also to a term in the sos and a corresponding term in the usable

list.

4 A Multi-level Marketing Enterprise

A multi-level marketing (MLM) enterprise [9] markets consumable products through

people as follows: A new distributor registers with the enterprise either as a direct asso-

ciate of the company, or under an existing distributor called an upline. Both the upline

(also called the sponsor) and the new distributor (now called a downline) then go on

to each sponsor more new distributors, and so on. In this way a network of distributors

of the products of the company is built. Hence, a MLM structure can be modelled by

forests and trees [13].

Distributors buy products from the company and every product carries a point value

(pv) as well as a business value (bv). The business value is directly related to the price

of the product. Both the points and the business values are accumulated per distributor

throughout a calendar month. At the end of the month the total business value in the

network for each distributor is calculated, and the distributor is paid (in the appropriate

currency) a certain percentage (determined by the pv) of the total business value for his

or her group. This is called a bonus.

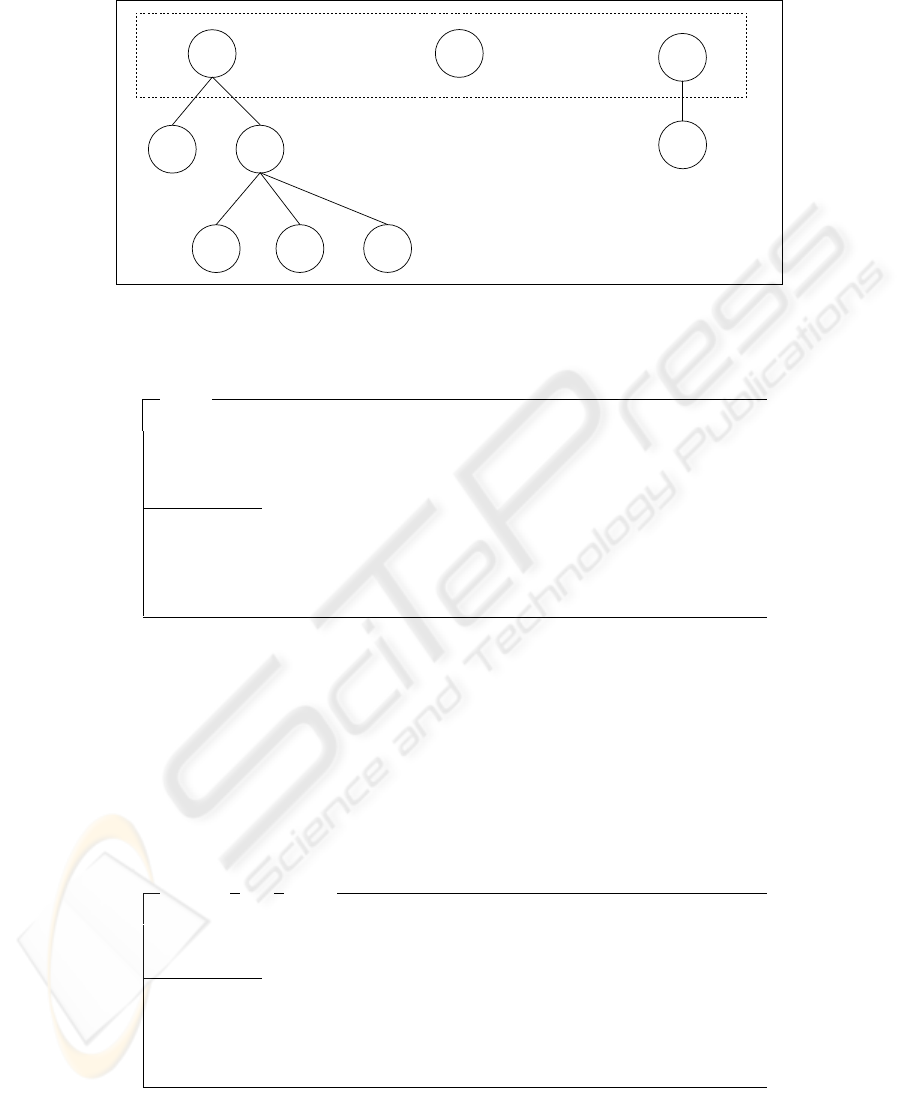
A small MLM network is shown in Fig. 1. Distributors A1, A2 and A3 associated

with the company directly are called the roots of the forest (or network in MLM terms).

The state of our MLM enterprise is (\ represents set-theoretic difference):

Fig. 1. An example network

MLM

known : P ID

NRoots : P ID

NUplines : ID ↔ ID

NDist : ID 7→ Name × Address × PV × BV × Bonus

known = dom NDist

dom NUplines ∪ ran NUplines ⊆ known

NRoots = known \ ran NUplines

Inj(NUplines)

The set known contains the identity codes of all distributors in the system. NRoots rep-

resents all root distributors. The relation NUplines represents the network of distribu-

tors while the function NDist represents a mapping from a unique identity code to the

particulars for that distributor. NDist is not necessarily injective since two (or more)

distributors may have the same particulars (i.e. name, address, etc.). Every distributor

has at most one upline, captured by the following general deﬁnition of injectivity:

(∀ R)(Inj(R) ↔ (∀ i)(∀ j)(∀ k)( ((i, k) ∈ R ∧ (j, k) ∈ R) −→ (i = j))) (1)

The following operation registers a new distributor p! below an existing one, q?:

with

upline

∆MLM

p!, q? : ID

name? : Name; addr? : Address

p! /∈ known ∧ q? ∈ known

known

= known ∪ {p!}

NUplines

= NUplines ∪ {q? 7→ p!}

NDist

= NDist ∪ {p! 7→ (name?, addr?, 0, 0.0, 0.0)}

A new identity code p! is generated by the system and the new distributor is linked to

q? in NUplines

. Initial product information pertaining to p! is reﬂected in the personal

pv being 0 and both the business value and potential bonus equal to the real value 0.0.

An order placed by a distributor is given by:

Order

∆MLM

id? : ID; pv? : PV; bv? : BV

id? ∈ known

(∃ pv : PV; bv : BV •

pv = third(NDist(id?)) + pv? ∧

bv = fourth(NDist(id?)) + bv? ∧

NDist

= NDist ⊕ {id? 7→

(ﬁrst(NDist(id?)), second(NDist(id?)),

pv, bv, ﬁfth(NDist(id?)))})

The functions ﬁrst, second, etc. project out an element at the appropriate position in the

tuple. NDist

is obtained from NDist by replacing the tuple with ﬁrst coordinate id? as

speciﬁed above. Many additional operations may be deﬁned on the state but are beyond

the scope of this paper. The interested reader is referred to [14].

Next we show how some of the heuristics introduced in Sect. 3 may be used to suc-

cessfully discharge two proof obligations that arise from the MLM speciﬁcation where

otherwise proofs are not easily arrived at.

5 Reasoning about the Speciﬁcation

Showing NRoots = known

\ ran NUplines

. Normally in Z a correct operation is as-

sumed to preserve the invariant. Nevertheless, a speciﬁer may want to verify the follow-

ing as a postcondition of schema Register

with

upline (Note that NRoots

= NRoots):

NRoots = known

\ ran NUplines

(2)

In effect the above predicate claims that the set of root elements is still equal to the

new set of all distributors (known

) minus the new set of all downline distributors

(ran NUplines

). If we deﬁne NewRoots = known

\ ran NUplines

and pose the nega-

tion of the following equality in the sos

NRoots = NewRoots (3)

then OTTER ﬁnds no proof in 20 minutes using a weight of 3, 4 or 5 and either posi-

tive or negative hyperresolution. Since neither form of hyperresolution is able to ﬁnd a

proof, we apply our inference rule selection heuristic and resort to binary resolution but

still using our weight template. Now the reasoner ﬁnds a proof after just 0.66 seconds.

Why does the reasoner fail to ﬁnd a proof for (3) using hyperresolution? The sos

format (3) requires the axiom of Extensionality [15]

(∀ A)(∀ B)[(∀ x)(x ∈ A ↔ x ∈ B) → (A = B)] (4)

to ‘open’ the equality in terms of elementhood to (loosely speaking) arrive at the fol-

lowing form of (3):

(∀ x)(x ∈ NRoots ↔ x ∈ NewRoots) (5)

The negation of (5) clausiﬁes into:

$c1 ∈ NRoots ∨ $c1 ∈ NewRoots (6)

$c1 /∈ NRoots ∨ $c1 /∈ NewRoots (7)

Formula (2) is unfolded in ﬁrst-order notation as

(∀ x)(x ∈ NRoots ↔ x ∈ known

∧ x /∈ ran(NUplines

))

and it clausiﬁes into

x /∈ NRoots ∨ x ∈ known

(8)

x /∈ NRoots ∨ x /∈ ran(NUplines

) (9)

x ∈ NRoots ∨ x /∈ known

∨ x ∈ ran(NUplines

) (10)

Note that positive hyperresolvents can be generated by resolving the sos clause (6) with

(8), but the sos clause (7) is not capable of generating a positive hyperresolvent with any

of the clauses (8) - (10). The result is that a proof attempt using positive hyperresolu-

tion cannot start off correctly. A similar problem occurs with negative hyperresolution.

Binary resolution creates no such problem, since binary resolvents may be mixed.

Still with this proof attempt, suppose a speciﬁer is initially, due to the weight clause,

concerned about an incomplete search for a proof. If we omit the weight template in the

above binary resolution proof then the reasoner again ﬁnds no proof in 20 minutes (as

opposed to a proof in 0.66 seconds). This forms the basis for a further heuristic that

may be applied to our last failed proof attempt.

In the proof of (3) we unfolded the predicate NUplines

= NUplines ∪ {q? 7→ p!}

in schema Register

with

upline into an ‘OTTER-like’ notation as

(all x)(El(x, NUplines

) ↔ El(x, NUplines) | El(x, Sin(ORD(q?, p!)))) (11)

using the following ﬁrst-order deﬁnition for a singleton:

(∀ x)(∀ y)(x ∈ Sin(y) ↔ x = y) (12)

Together with deﬁnition (11), we also needed the following fact about ordered pairs

from [15]:

(∀ u)(∀ v)(∀ w)(∀ x)(ORD(u, v) = ORD(w, x) ↔ ((u = w) ∧ (v = x))) (13)

Upon studying the clauses generated by the search for a proof, we note that (12) and

(13) interact to generate literals of the form El(ORD(x, y), Sin(ORD(u, v))) where x, y,

u and v are variables. This literal contains nested functors, a practice discouraged by

our heuristic #3, since it, in the absence of a weight template, leads to a large number

of unnecessary uniﬁcations.

If we, therefore, rewrite (11) as

(all x)(El(x, NUplines

) ↔ El(x, NUplines) | (x = ORD(q?, p!))) (14)

and still omit the weight template, then OTTER again ﬁnds a proof for (3), but in 3.70

seconds. According to our element structure heuristic #7 we can further rewrite (14) as

(∀ y)(∀ z)

(ORD(y, z) ∈ NUplines

↔ (ORD(y, z) ∈ NUplines ∨ (y = q? ∧ z = p!))) (15)

which cuts the execution time of 3.70 seconds down to just 0.06 seconds.

Cardinality proof. After the execution of operation Register

with

upline we expect

the following to hold regarding the cardinality of the set known

= known ∪ {p!}:

#known

= #known + 1 (16)

We use the following two deﬁnitions of cardinality (Card(A, n) denotes #A = n)

(∀ A)(Card(A, 0) ↔ A = ∅) (17)

(∀ A)(∀ n)(Card(A, n + 1) ↔ (∃ x)(x ∈ A ∧ Card(A − {x}, n))) (18)

Suppose we start with the precondition Card(known, n) and pose the following question

in the sos:

−Card(known

, n + 1) (19)

OTTER ﬁnds no proof for (19) in 30 minutes and closer investigation reveals that the

term Card(A − {x}, n) above contains nested functors (i.e. a singleton deﬁnition inside

a set difference inside the functor Card), a practice discouraged by our nested functor

heuristic. As a ﬁrst step we unfold deﬁnition (18) as:

(∀ A)(∀ n)(Card(A, n + 1) ↔

(∃ B)(∃ x)(x ∈ A ∧ Card(B, n) ∧ (∀ y)(y ∈ B ↔ y ∈ A ∧ y /∈ {x}))) (20)

With this unfolding OTTER still ﬁnds no proof, but since such unfolding is in turn

against the recommendation put forward by the intermediate structure heuristic we re-

place the deﬁnition of set B in (20) with

(∀ y)(y ∈ B ↔ y ∈ DIFF(A, {x})) (21)

where x is still existentially quantiﬁed as in (20) and DIFF is deﬁned by:

(∀ x)(x ∈ DIFF(known

, {p}) ↔ x ∈ known

∧ x /∈ {p}) (22)

With these deﬁnitions OTTER ﬁnds a short proof for (19) in just 0.21 seconds. Deﬁni-

tion (22) is in line with our multivariate functor heuristic which advocates cutting down

on the number of variables as arguments of functors. This is mainly the reason why the

nested functor in deﬁnition (21) turns out to be harmless. For example, if we rewrite

(22) above as

(∀ A)(∀ p)(∀ x)(x ∈ DIFF(A, {p}) ↔ x ∈ A ∧ x /∈ {p}) (23)

then OTTER again ﬁnds no proof in 20 minutes. Replacing one of the variables (say A)

in (23) above with a constant again helps OTTER to ﬁnd a proof in 8.59 seconds.

We may also ﬁt our search-guiding heuristic onto the last deﬁnition of Card above.

The technique of resolution by inspection reveals that the sos question (19) needs just

the ‘if-direction’ of (20). If we make such adjustments we can even ﬁnd a proof using

(23), but in 1 minute 27 seconds.

6 Summary and Future Work

This paper illustrated how some set-theoretic reasoning heuristics previously developed

may be used to discharge two proof obligations that arise from the speciﬁcation of a

multi-level marketing enterprise. We showed that the same PO may be discharged in

more than one way. This is signiﬁcant, since if a particular heuristic fails to deliver then

another one may be applied instead. The full suite of heuristics deﬁned in Sect. 3 have

been shown to be useful in reasoning about the properties of an extended version of the

Information Enterprise described in Sect. 4 of this paper. Details appear in [16].

A number of problem areas, however, remain: Our enterprise model is inherently

recursive, resulting in the reasoner experiencing difﬁculty when reasoning about recur-

sive structures. For example, using our traditional deﬁnitions of cardinality (17) and

(18) allows the reasoner to easily prove that the cardinality of the empty set is 0, or

the cardinality of a singleton equals 1. If we, however, pick a set with two elements,

say X = {2, 3}, then OTTER fails to ﬁnd a proof of the property #X = 2 in 20 min-

utes using any of our heuristics listed above. More work will have to be undertaken to

successfully guide the reasoner through the mineﬁeld of recursion.

Further empirical work is also called for to scale up the proofs reported on in this pa-

per to industrial sized proof attempts and we anticipate that additional heuristics would

have to be developed to address the challenges that may unfold from such experiments.

References

1. Bowen, J.P.: Z: A formal speciﬁcation notation. In Frappier, M., Habrias, H., eds.: Software

Speciﬁcation Methods: An Overview Using a Case Study. FACIT. Springer-Verlag (2001) 3

– 19

2. Woodcock, J., Davies, J.: Using Z: Speciﬁcation, Reﬁnement, and Proof. Prentice-Hall,

London (1996)

3. Fagan, M.: Design and code inspections to reduce errors in program development. IBM

Systems Journal 15 (1976) 182 – 211

4. Mokkedem, A., Hosabettu, R., Jones, M.M., Gopalakrishnan, G.: Formalization and proof

of a solution to the PCI 2.1 bus transaction ordering problem. Formal Methods in Systems

Design 16 (2000) 93 – 119

5. van der Poll, J.A., Labuschagne, W.A.: Heuristics for Resolution-Based Set-Theoretic

Proofs. South African Computer Journal Issue 23 (1999) 3 – 17

6. Boyer, R., Lusk, E., McCune, W., Overbeek, R., Stickel, M., Wos, L.: Set Theory in First-

Order Logic: Clauses for G

odel’s Axioms. Journal of Automated Reasoning 2 (1986) 287 –

327

7. Bundy, A.: A Survey of Automated Deduction. Technical Report EDI-INF-RR-0001, Divi-

sion of Informatics, University of Edinburgh (1999)

8. Wos, L., Pieper, G.W.: A Fascinating Country in the World of Computing: Your Guide to

Automated Reasoning. World Scientiﬁc Publishing Company (1999)

9. Golden Neo-Life Diamite International: Distributor Business Guide: The Business Plan.

(1997)

10. McCune, W.W.: OTTER 3.3 Reference Manual. Argonne National Laboratory, Argonne,

Illinois. (2003) ANL/MCS-TM-263.

11. Quaife, A.: Automated Development of Fundamental Mathematical Theories. Automated

Reasoning Series. Kluwer Academic Publishers (1992)

12. Wos, L.: The Resonance Strategy. Computers and Mathematics with Applications 29 (1995)

133 – 178 (Special issue on Automated Reasoning).

13. Scheurer, T.: Foundations of Computing : System Development with Set Theory and Logic.

International Computer Science Series. Addison-Wesley (1994)

14. van der Poll, J.A., Kotz

e, P.: A Multi-level Marketing Case Study: Specifying Forests and

Trees in Z. South African Computer Journal Issue 30 (2003) 17 – 28

15. Enderton, H.: Elements of Set Theory. Academic Press, Inc. (1977)

16. van der Poll, J.A.: Automated Support for Set-Theoretic Speciﬁcations. PhD thesis, Univer-

sity of South Africa (2000)