
Health care and social inference systems:
An unauthorized inference control based on fuzzy logic
Souhila Kaci
1
, Abdeslam Ali-Laouar
2
, and Fr
´
ed
´
eric Cuppens
2
1
Centre de Recherche en Informatique de Lens (C.R.I.L.–C.N.R.S.)
Rue de l’Universit
´
e SP 16 62307 Lens France
2
Institut de Recherche en Informatique de Toulouse (I.R.I.T-C.N.R.S)
118 route de Narbonne 62077 Toulouse France
Abstract. In this paper, we address the problem of unauthorized inference of
confidential information in the field of health care and social information systems.
More precisely, we will focus on the problem of inference control of confidential
information from statistical databases which contain information about patients
and propopse a method based on fuzzy logic to avoid unauthorized inference.
Information provided using our approach remains relevant because it is without
loss of quality.
1 Introduction
The security of information systems is a very important problem which has been mainly
addressed in military applications. This led to security policies which are applicable
only in environments which accept a rigid bluk-heading of information and services
handling this information. Indeed, these models cannot be used in other domains which
also require security policies like for example the health care domain where it is impor-
tant to guarantee the confidentiality, integrity and availability of pieces of information
contained in medical files of patients. The confidentiality consists in expressing who
has the right to reach which information about which, when, and possibly under which
conditions. The integrity is the property which ensures that information is modified only
by the users authorized under the conditions normally envisaged. Lastly, the availabil-
ity is the aptitude of an information system for being able to be employed by the users
competent under the conditions of accesses and use normally envisaged.
In this paper, we particularly address the problem of security of information systems
in the field of health care and social. Let us note that in spite of the development of
security policies in this context [6, 7], it is always possible for an external attacker and,
especially, for an internal user badly disposed, to try to circumvent the mechanisms of
access control to the resources in order to attack the confidentiality, the integrity or the
availability of information.
To prevent the infringements against the intimacy of the patients, the medical databases
must protect not only confidential information, but also information not explicitly con-
fidential which can be employed to obtain confidential information. This paper treats
Kaci S., Ali-Laouar A. and Cuppens F. (2004).
Health care and social inference systems: An unauthorized inference control based on fuzzy logic.
In Proceedings of the 2nd International Workshop on Security in Information Systems, pages 217-226
DOI: 10.5220/0002674902170226
Copyright
c
SciTePress

detection and the limitation of the situations for which there is a risk of illegal infer-
ence (called also illegitimate inference). This problem is called unauthorized inference
problem. It can also be simply defined in the following way. Suppose that a user is au-
thorized to access to some information. The crucial question now is: can this user use
this information to deduce a confidential information for which she would not have the
right of access? A possible solution to this problem is to refuse to answer when this
may allow to deduce confidential information however this solution is not interesting
because it does not respect the availability condition. Another possible solution is the
use of false answers for users having a restricted access to the information system. In-
deed this method allows to protect confidential information by providing false but not
very significant answers. The problem of this method is that the user to whom one pro-
vides false answers can make bad decisions. It is also difficult to provide a coherent set
of false answers. The solution that we propose in this paper does not consist to provide
a false answer to the user but a ”vague” information formalized in fuzzy logic [8, 4].
Section 2 describes the problem of illegitimate information from databases contain-
ing information about the patients. We also describe a well-known method to attack
such databases. In section 3, we first present the general principle of our approach. We
then give some necessary background on fuzzy logic on which our approach is based.
Lastly, section 4 gives a detailed description of our approach.
2 Illegitimate inference in statistical databases
The main difference between a statistical database (SDB for short) and a traditional one
relates to the interrogation interface more limited in the SDB. The queries on a SDB are
limited to operations like counting (COUNT), sum (SUM), the average (AVG) and other
statistical calculus, which are carried out on subsets of data. Although these operations
seem to be without consequence, it should be made sure that significant information on
the individuals are not revealed. This problem becomes particularly difficult if we ac-
cept the possibility that a sequence of general queries, each one by itself does not allow
to deduce confidential information, can be employed to deduce significant information.
Let us now give an example to illustrate the difficult nature of the inference problem
in the statistical databases. We consider a database, given in Table 1, which contains
Table 1. Example of a statistical database.
Name Sex Age Department salary
Jean M 27 Mathematics 2.000
Thomas M 43 computer science 3.000
Name Sex Age Department salary
Isabelle F 27 Mathematics 2.600
Justine F 31 computer science 3.200
information concerning the employees. Let us suppose that the policy of the company
imposes that the salary of the employees is a confidential information which should
not be revealed. To achieve this goal, the database does not return an answer to a query
like: how much is the salary of the employee whose name is Isabelle? since the answer
218

is confidential. Similarly, the base does not answer any query when, for example, the
average is calculated on the basis of a simple record, i.e. a query concerning only one
individual. Consequently, it refuses to answer for example the query: how much is the
average salary of the women employees who work for the computer science depart-
ment? because the average here is calculated from only one record.
A query on a SDB R consists to compute a subset of R using a characteristic formula
C, which is a logical formula built from the values of the attributes of R by using the
logical operators ∧ (and), ∨ (or), and ¬ (not). For example, the subset of records rep-
resenting the women employees who work for the computer science department, can be
represented by the following characteristic formula:
C = (sex=F) ∧ (department=computer science).
The set of records which satisfy the characteristic formula C, denoted by X
C
, is called
the result of the query. Applying the formula C on the relation R given in Table 1, we
get: COUNT (C) = 1, AV G(Age, C) = 31 and SUM(Salary, C) = 3200.
Generally, a statistical query taken separately does not allow to deduce confidential
information. For this reason, a user with good intentions should be able to form any
interesting characteristic formula, and to carry out any statistical measurement on the
resulting set of the records. However, it is possible that a user forms statistical queries
which can be employed to deduce specific values of a field of the database, which is not
acceptable if the values represent confidential information. In this case, we say that the
database has been compromised.
A characteristic formula used in order to compromise a database is called a tracker
[2, 3]. This formula is chosen so that it gives as a result a set X
C
whose size is equal
to 1. Denning et col. [2] have shown that for any real database, a tracker can always be
found.
In the next section, we propose a new strategy to prevent attacks based on trackers.
3 Our approach
In the everyday life and particularly in the medical field, medical analyses are gener-
ally expressed by linguistic descriptions (Example: Temperature of the body is raised,
normal, etc). This is especially used for the non-specialists in the medical field. In this
paper, we take as a starting point this method to deal with the illegitimate inference
problem in statistical databases. More precisely, we replace the results of the statistical
queries (quantitative answers) by linguistic descriptions (qualitative answers) in order
to limit the risk of illegitimate inference.
For this, our idea consists in replacing the numerical answers (e.g. numbers of patients
= 10) by linguistic descriptions (e.g. medium) formalized in fuzzy logic framework.
Intuitively, each numerical answer is associated to a given class then a qualitative an-
swer is associated to each class. Thus, the formalization of our approach requires two
steps: classification and fuzzification. Let us recall these two concepts:
– Classification is the procedure which consists in decomposing the scale of the used
numerical values into non-empty classes so that each numerical value belongs to
one and only one class.
Let I be a set of elements. We say that Q(I) is a partition of I if there exists a set
219

{q
1
, q
2
, · · · , q
k
} satisfying the following conditions:
S
i=1,···,k
q
i
= I with q
i
6= ∅ and q
i
∩ q
j
= ∅ for i 6= j.
To be relevant, a partition should be made up of definitely individualized classes.
Among existing classification methods, we recall one method, that we will use later,
based on the aggregation around the centers using a fixed number of classes. The
principle of this method is to determine a partition of I composed of k classes, the
number k being fixed a priori by the user of the method. k centers c
1
, · · · , c
k
are
chosen which are either arbitrarily points in the space of the variables, or elements
of the set I.
Each element of the set I is associated to one and only one class whose center is
one of the k centers c
1
, · · · , c
k
according to the following assignment rule:
i belongs to the class q
j
of center c
j
iff ||i − c
j
|| = min
l=1,···,k
||i − c
l
||.
After the classification step, we have to associate an appropriate linguistic variable
to each class. For example, if the numerical scale corresponds to the temperature
then the linguistic variable which corresponds to the interval [20, 25] may be tepid.
This can be formalized in fuzzy logic [8].
– Fuzzification: A principal characteristic of the human reasoning is that it is based
on vague or incomplete data. Thus, to determine if a temperature is hot or cold
is easy for any individual without necessarily knowing its exact value. Fuzzy logic
has the aim of studying the representation of vague knowledge and the approximate
reasoning. A principal characteristic of fuzzy logic is that an object may belong to
a set and at the same time to its complement. Thus, a temperature of 22 may at the
same time be hot and not hot.
A linguistic variable is a triple (X, V, F
X
), where X is a variable (age, temper-
ature, etc) defined on a set of reference V (the set of integers, reals, etc). F
X
=
{A
1
, A
2
, · · ·} is a finite or infinite set of subsets of V used to characterize X (old,
young, hot, cold, etc). Each fuzzy subset represents a linguistic description.
The variable may belong to one or more subsets of this element of reference. For
example, the temperature T = 28 may belong to the subset ”pleasant” but may also
belong partly to the subset ”hot”.
The membership relation between a variable and a subset is called membership
function. In other terms, we speak about the membership degree of a variable x to
a subset F , denoted by µ
F
(x).
A fuzzy set F of universe Ω (a fuzzy subset of Ω) is defined by a membership func-
tion µ
f
which associates to each element x of Ω a value in the interval [0, 1].
µ
F
: Ω → [0, 1]
x 7→ µ
F
(x)
µ
F
(x) represents the membership degree of x to the set F . By definition, if µ
F
(x) =
0 then x does not belong to F and more µ
F
(x) approaches 1, more the value x be-
longs to F . If µ
F
(x) = 1 then x belongs completely to F .
A fuzzy subset is said to be convex if and only if:
∀x, y; x > y, ∀z ∈ [x, y], µ
F
(z) ≥ min(µ
F
(x), µ
F
(y)).
Generally, we express numerical quantities by vague linguistic descriptions such as
”approximately 100”. The results of fuzzy measurements or an error analysis are
220

modelled by fuzzy sets called fuzzy quantities. A fuzzy quantity Q is a fuzzy set in
the universe R of real numbers. It is supposed to be normalized.
A fuzzy interval N is a convex fuzzy quantity. It is a generalization of a real interval
whose extremities are fuzzy in order to model concepts such as ”approximately”,
”roughly”, etc.
– Representation of a L-R fuzzy interval A fuzzy interval of type LR has a mem-
bership function built from a quadruplet A = (m
1
, m
2
, a, b), where m
1
, m
2
, a and
b are strictly positive real numbers, and of two functions L and R from R
+
into the
interval [0, 1] semi-continuous, non-increasing and satisfying the conditions:
– L(0) = R(0) = 1,
– L(1) = 0 or ∀x ∈ R
+
, L(x) > 0 and lim
x→+∞
L(x) = 0,
– R(1) = 0 or ∀x ∈ R
+
, R(x) > 0 and lim
x→+∞
R(x) = 0.
The membership function is defined as follows:
µ
F
(x) =
L(
m
1
−x
a
) if m
1
− a ≤ x ≤ m
1
1 if m
1
< x < m
2
R(
x−m
2
b
) if m
2
≤ x ≤ m
2
+ b
0 if x < m
1
− a or x > m
2
+ b
When m
1
= m
2
= m, the fuzzy interval P = (m, m, a, b)
LR
is called a fuzzy
number, denoted by P = (m, a, b)
LR
and whose membership function is defined
as follows:
µ
F
(x) = L(
m−x
a
)if x < m, µ
F
(x) = 1if x = m and µ
F
(x) = R(
x−m
b
)if x > m.
Let P
1
= (p
1
, α
1
, β
1
)
LR
and P
2
= (p
2
, α
2
, β
2
)
LR
be two LR-fuzzy numbers.
Then the addition ⊕, the substraction ª and multiplication ⊗ are defined by [4]:
P
1
⊕ P
2
= (p
1
+ p
2
, α
2
+ α
2
, β
1
+ β
2
)
LR
.
P
1
ª P
2
= (p
1
− p
2
, α
1
+ α
2
, β
1
+ β
2
)
LR
.
P
1
⊗ P
2
= (p
1
∗ p
2
, p
1
∗ α
2
+ p
2
∗ α
1
, p
1
∗ β
2
+ p
2
∗ β
1
)
LR
.
Contrary to the addition and subtraction, the multiplication P
1
⊗ P
2
is not of
type LR. An approximate value of type LR is given when P
1
and P
2
have a
support included in R
+
, α
1
and β
1
are small w.r.t. p
1
and, α
2
and β
2
are small
w.r.t. of p
2
.
To apply a linguistic representation to a quantitative variable, the principle consists
in breaking up all possible values of the given quantitative variable into subsets (a
set of classes of values), so that the borders of the classes are not clearly given. This
treatment allows to transform a numerical input into a fuzzy subset. The decompo-
sition should not be arbitrary but founded on criteria, such as the homogeneity of
the classes, the uniform partition of the universe, the subsets are totally ordered.
These subsets are also called ”linguistic variables”.
The subsets are characterized by their associated membership functions; we asso-
ciate a membership function to each subset. Their positions and overlappings can
be chosen arbitrarily provided that the following conditions are verified: their form
should be convex, the subsets (often in the form of trapezoid) should be partially
overlapped so that there are no unspecified ranges and lastly to avoid to imbricating
more than two subsets.
221

00
10
20
T
=
31
40
50
µµ
11
−
10
−
20
V
e
r
y
c
o
l
d
t
e
m
p
e
r
a
t
u
r
e
s
C
o
l
d
t
e
m
p
.
P
l
a
i
s
ea
n
t
t
e
m
p
e
r
a
t
u
r
e
s
H
o
t
t
e
m
p
e
r
a
t
u
r
e
s
V
e
r
y
h
o
t
t
e
m
p
e
r
a
t
u
r
e
s
TT
0
.
6
0
.
35
Fig. 1. Representation of the temperature in fuzzy logic.
Example 1. Let us consider the temperature input T = 31. According to the mem-
bership function given in Figure 1, we obtain the following values:
µ
T
(very cold temperatures) = µ
T
(cold temperatutres) = 0, µ
T
(pleasant temperatures) =
.6, µ
T
(hot temperatures) = .35 and µ
T
(very hot temperatures) = 0.
Now, it seems important to answer some questions : How many classes is it nec-
essary to represent each quantitative variable? Which are the best linguistic val-
ues for each class? For the first question, more the number of linguistic values is
high, more the partitioning quality is good. It is necessary however that the rate:
Card(Ω)/Number of Partitions is not equal to 1, otherwise this simply means that
there is no fuzzification.
For the second question, we compute the membership degree of each element x to
all the subsets F
i
of the universe Ω. Let µ
F
i
(x) be the membership degree of x to
F
i
. We say that x ∈ F
i
only if ∀F ∈ Ω, µ
F
(x) ≤ µ
F
i
(x).
4 Detailed description of our approach
The principle of our method consists, in a first step, to decompose the set of values of
the confidential attributes into subclasses of values. Each subclass contains values ac-
cording to a given criterion. In this paper, we will use the classification method based
on a fixed number of classes.
After the classification into subclasses the fuzzification comes. We transform each class
into a fuzzy quantity i.e., a fuzzy number with a membership function. Then, we as-
sociate a linguistic variable to each number (small, large, etc). Next, for each answer
provided by the database management system, we compute the membership degree of
this answer to each fuzzy subset (linguistic variables). The answer of our system is the
linguistic variable which has the highest membership degree.
Let us note that the simplest version of a statistical query SQL is written as follows:
SELECT f( <attributes>) FROM <relations> WHERE <conditions>,
where f is a statistical function such as Sum, Avg, Count, etc.
In this paper, we focus on queries which compute statistical quantities, i.e. queries
which deduce information on aggregation such as sum, average, max and min.
Let us consider the example of relation R (patient, H/F, age, sickness insurance com-
pany, leucocyte rate) given in the Table 2 (borrowed from [5]).
The number of patients is 10 and the normal leucocyte rate in mm3 of blood is 4500.
In this example, we suppose that the leucocyte rate is a confidential attribute. To control
the illegitimate inference on this attribute, we will transform the answers to the queries
222
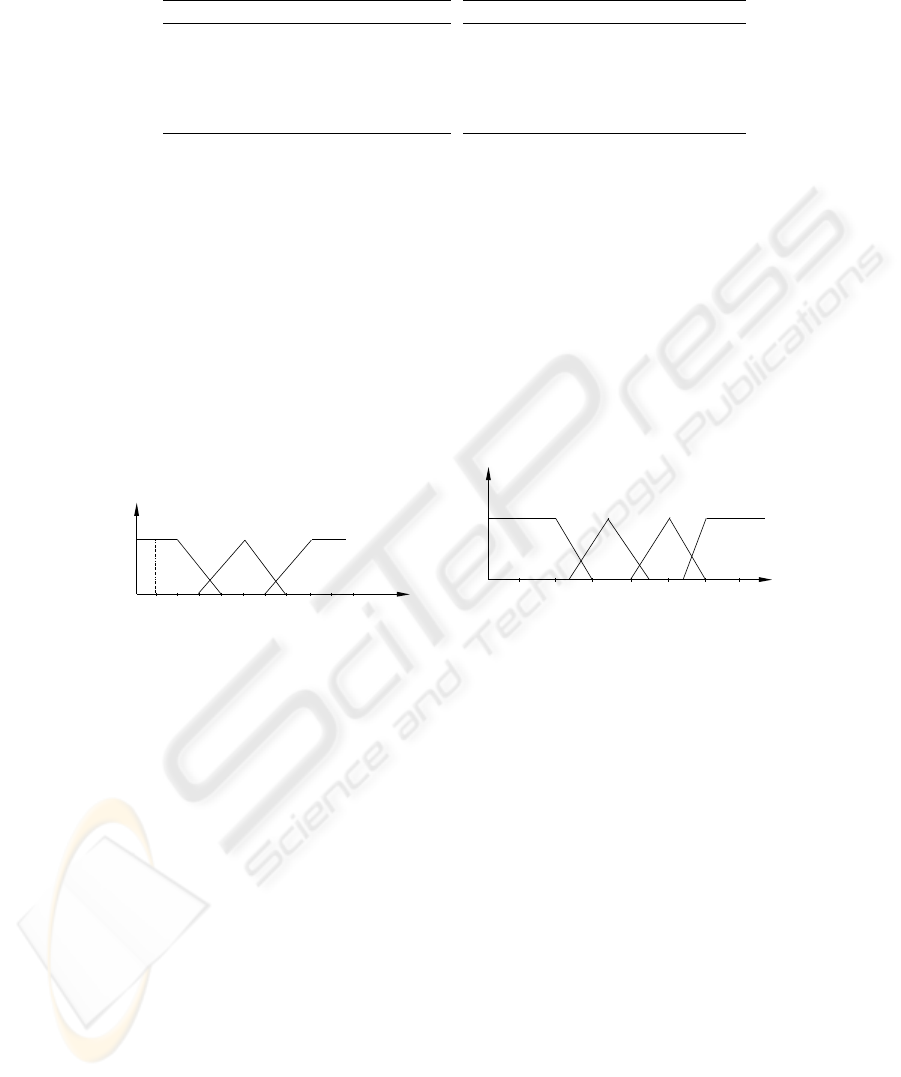
Table 2. Example of a database.
Patient M/F Age Sick. ins. Leucocyte
Dufour M 45 MAAF 4000
Dulac F 35 MMA 7000
Dulon M 55 MGEN 3500
Dumas M 40 Rempart 3800
Dumont M 38 MMA 7500
Patient M/F Age Sick. ins. Leucocyte
Dupont M 30 MMA 6000
Dupr F 32 IPECA 7200
Dupuis F 50 MGEN 6800
Durand F 25 LMDE 3000
Duval M 45 IPECA 5500
concerning this attribute by giving qualitative answers.
We proceed in the same way for the answers to the queries which compute the number
of patients who verify a given condition. For this, we fuzzify the number of patients and
the leucocyte rate.
Let us start with the number of patients and decompose this variable as follows: A first
class: from 0 to 3, a second class: from 4 to 6 and a third class: from 7 to 10.
We now transform each class into a fuzzy number A
i
(m, a, b) where m is the center of
the class, a and b represent the degrees of inaccuracy.
For each number, we associate a linguistic variable (see also Figure 2-a):
– The first class is fuzzified by the fuzzy number ”small” = (2, 2, 2)
LR
,
– The second class is fuzzified by the fuzzy number ”medium” = (5, 2, 2)
LR
,
– The third class is fuzzified by the fuzzy number ”great” = (8, 2, 2)
LR
.
11
22
33
44
55
66
77
88
99
10
µµ
11
S
m
a
ll
M
e
d
i
u
m
G
r
ea
t
N
u
m
b
e
r
o
f
p
a
t
i
e
n
t
s
L
e
u
c
o
c
y
t
e
r
a
t
e
µµ
1000
2000
3000
4000
5000
6000
7000
11
A
cce
p
t
a
b
l
e
W
ea
k
G
ood
H
i
g
h
Fig. 2. (a) Fuzzification of the number of patients. (b) Fuzzification of the leucocyte rate.
We now classify the leucocyte rate for a patient as follows:
– 1
st
class: from 0 to 3000, 2
nd
class: from 3000 to 4500,
– 3
rd
class: from 4500 to 6000 and 4
th
class: from 6000 to 7000.
We now propose the following fuzzification (see also Figure 2-b):
– The first class is fuzzified by the fuzzy number ”weak” = (2000, 1000, 1000)
LR
– The second class is fuzzified by the fuzzy number ”acceptable” = (3500, 1000, 1000)
LR
– The third class is fuzzified by the fuzzy number ”good” = (5000, 1000, 1000)
LR
– The fourth class is fuzzified by the fuzzy number ”high” = (6000, 1000, 1000)
LR
Let us now suppose that a user is authorized to carry out statistical queries and she
wants to discover the leucocyte rate of ”Dulon”. Let us also suppose that this user knows
moreover that ”Dulon” has the MGEN as a sickness insurance company. Consider now
the following queries:
1) SELECT Count(Patient) FROM R WHERE M/F=’M’ AND Sick. ins. =’MGEN’
223

Result = 1 (R
1
)
Let us compute the membership degrees µ
F
i
(R
1
) of the result (R
1
) w.r.t. each
fuzzy subset. We get: µ
small
(R
1
) = 1, µ
medium
(R
1
) = 0 and µ
great
(R
1
) = 0.
So the answer provided after fuzzification is ”small” since it corresponds to the
highest membership degree.
2) SELECT AVG(Leucocyte) FROM R WHERE M/F=’M’ AND Sick. ins. = ’MGEN’
Result = 3500 (R
2
)
We compute the membership degrees µ
F
i
(R
2
) of the result (R
2
) w.r.t. each fuzzy
subset: µ
weak
(R
2
) = µ
good
(R
2
) = µ
high
(R
2
) = 0 and µ
acceptable
(R
2
) = 1.
Then the answer is ”acceptable”.
Note that the deduction of confidential information when handling numerical an-
swers is very easy. It is clear that from (R
1
) and (R
2
), the user may directly deduce
that the leucocyte rate of ”Dulon” is equal to 3500.
The case of the qualitative answers is less simple: from (R
1
), the user knows that
the size of the set to which ”Dulon” belongs is ”small”, and from (R
2
), she deduces
that their average of the leucocyte rate (the set ”small”) is ”acceptable”.
Let us now see what may the user deduce from these two information. For this, we
know that the average is defined by the equation
x =
1
n
P
x
i
. It is clear that when
n is equal to 1, the average is equal to x
i
. To see the impact of the fuzzification on
the reasoning of the user, we will analyze the use of the fuzzification step by step:
– Let us suppose that the number of patients is not fuzzified whereas the leucocyte
rate is. The answer given to the user in this case is then: the number of patients
is equal to 1 (as an answer to the query (R
1
)) and their average leucocyte rate
is ”acceptable”, which allows to deduce that the leucocyte rate of Dulon is
”acceptable”. However, the fuzzification of the number of patients makes that
the answer provided to the user (also as an answer to the query (R
1
)) is ”small”,
which does not allow to know precisely how many patients correspond to this
answer ”small”.
– Let us now suppose that the user knows moreover that the maximum size of the
fuzzy quantity ”small” is equal for example to two. However even if the user
has this information, she deduces nothing as we will show on the following
example: It is known that an ”acceptable” leucocyte rate lies between 3000
and 4500. Let the size of ”small” be equal to 2. From a leuycocyte average
of two patients x
1
and x
2
equal to ”acceptable”, we may have the following
possibilities for x
1
and x
2
:
– x
1
= 2500 ≡ ”weak”
3
, x
2
= 4000 ≡ ”acceptable”
– x
1
= 2500 ≡ ”weak”, x
2
= 5000 ≡ ”good”
– x
1
= 1500 ≡ ”weak”, x
2
= 6500 ≡ ”high”
– x
1
= 3500 ≡ ”acceptable”, x
2
= 5000 ≡ ”good”
– x
1
= 3500 ≡ ”acceptable”, x
2
= 4000 ≡ ”acceptable”.
From these results, one can say that from a leucocyte average equal to ”accept-
able” computed for two patients, one concludes nothing on the leucocyte rate
of one of the two patients.
3
The equivalence means here that the number (e.g. 2500) corresponds to the given class (e.g.
”weak”) after fuzzification.
224

Note that to have an average rate ”acceptable”, we have five possibilities for
the leucocyte rate for each of the two patients. In only one case, the rate of
the two patients is ”acceptable”. In the other cases, it varies between ”Weak”,
”acceptable”, ”Good” and ”High”. So we have four cases with x
1
or x
2
equal
to ”acceptable” and six cases different from ”acceptable”.
Then we may say that it is totally possible that the leucocyte rate of ”Dulon”
is equal to ”acceptable”, but it is also totally possible that it is different from
”acceptable”. Indeed, we are in a situation of total ignorance.
Let us note that in the real case, the database may contain thousands of patients and
the fuzzy quantity ”small” may reach several hundreds of patients. Consequently,
the possibilities of inference are even weaker when the cardinality which corre-
sponds to the fuzzy quantity is larger. The user deduces nothing on the leucocyte
rate of ”Dulon” when all the possible cases are considered.
3) SELECT Count(Patient) FROM R. Then, Result = 10 (R
3
)
The answer after fuzzification is ”great” (R
0
3
)
The user tries thereafter to know the number of patients different from ”Dulon”. For
this, she gives the following query:
4) SELECT Count(Patient) FROM R WHERE NOT (M/F=’M’ AND Sick. ins.=’MGEN’);
Result = 9 (R
4
)
The answer after fuzzification is ”great” (R
0
4
)
From these two answers, the user may construct the following reasoning: The dif-
ference between (R
3
) and (R
4
) (10-9=1) corresponds to the number of male pa-
tients who have the MGEN as a sickness insurance company (i.e., the number of
patients having the same properties as ”Dulon”).
With a similar reasoning, she concludes that the difference between (R
0
3
) and (R
0
4
)
is equal to
4
| ”great” ª ”great” |= | (8, 2, 2)
LR
ª (8, 2, 2)
LR
| =| (8, 2, 2)
LR
⊕
(−8, 2, 2)
LR
| =| (0, 4, 4)
LR
| which is equivalent to (0, 0, 4)
LR
after removing
the negative part, since there is no negative leucocyte rate.
So we have (R
0
3
) ª (R
0
4
) ∼ ”small”. Indeed, we get the same result as for (R
1
)
after fuzzification.
To know the average of the leucocyte rate for all the patients, the user gives the
following query:
5) SELECT AVG(Leucocyte) FROM R. Then, Result = 5430 (R
5
)
The answer after fuzzification is ”good” (R
0
5
)
To compute the average of the leucocyte rate of all the patients different from ”Du-
lon”, the user gives the following query:
6) SELECT AVG(Leucocyte) FROM R WHERE NOT (M/F=’M’ AND Sick. ins.=’MGEN’),
Result = 5644 (R
6
)
The answer after fuzzification is ”high” (R
0
6
)
In the case of numerical answers, to know the leucocyte rate of ”Dulon”, the user
computes the following value: 10 ∗ 5430 − 9 ∗ 5644 = 3500.
With a similar reasoning, in the case of qualitative answers, she may try to proceed
4
Since the values are not known a priori but supposed to be positive, the subtraction is translated
into fuzzy logic by the absolute value.
225

in the following way. The leucocyte rate of ”Dulon” is equal to:
| ((R
0
3
) ⊗ (R
0
5
)) ª ((R
0
4
) ⊗ (R
0
6
)) | ∼| (−8000, 38000, 38000)
LR
|.
From the obtained number, the user deduces nothing because the leucocyte rate is
never negative. Even if she can deduce some information (if the fuzzification is
changed), the situation is similar to the first case since the user does not know the
exact number of patients. Let us also note that we lost the precision on the com-
putation of the leucocyte rate because of the multiplication which we carried out
(recall that in the case of the multiplication, the computation is only approximate).
We have shown on this example that the user may use different ways to deduce con-
fidential information however the use of qualitative answers makes difficult the imple-
mentation of attacks by trackers because after fuzzification, it is difficult to identify the
individual concerned by the confidential information. Indeed, required information is
not distinguished after fuzzification.
5 Conclusion
We have proposed a first attempt to limit the risk of inference of confidential information
from a database using fuzzy logic. It is difficult to affirm here that we eliminate any
risk of illegal inference. The goal is nevertheless to continue to answer the queries as
well as possible using non-confidential information. So our aim is to limit at least as
possible the restrictions of legitimate access on databases while ensuring that the risk
of unauthorized inference remains below an acceptable threshold.
An immediate prospect for this work would be to implement our approach and to
validate it on great databases. We showed in this paper that our approach particularly
enables us to control the attacks by trackers. We expect to see how this approach could
be used to control other types of attacks like linear systems [2, 1]. Lastly, it would be
interesting to see to what extent our approach is sensitive to the classification method
used, i.e. to see if the use of other classification methods give sensitively different re-
sults.
References
1. F. Cuppens. A logical analysis of authorized and prohibited information flows. In IEEE Sym-
posium on Research in Security and Privacy, 1993.
2. D. Denning, P. Denning and Schwartz. The tracker: A Threat to Statistical Database Security.
ACM Transactions on Database Systems, 4(1): 76-96, 1979.
3. D. Denning and J. Schlorer. A Fast Algorithm for Calculating a Tracker in Statistical Databse.
ACM Transactions on Database Systems, 5(1), 1980.
4. D. Dubois and H. Prade. La logique floue. In Quaderni, 50-73, 1995.
5. A.A. El Kalam. MP6, Sous-projet 3: Politiques de scurit pour les SICSS. Informations protger
et menaces. Rapport technique.
6. R. Sandhu, E. Coyne, H. Feinstein and C. Youman. Role-based access control models. IEEE
Computer, 29:38-47, 1996.
7. S. Solms. The management of computer security profiles using a role-oriented approach. Com-
puter and Security, 13(8), 673-680, 1994.
8. L. Zadeh. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets and Systems, 1, 3-28,
1978.
226
