
On the Role of the Inner State Size in Stream Ciphers
Erik Zenner
University of Mannheim (Germany)
Abstract. Many modern stream ciphers consist of a keystream generator and an
initialisation function. In fielded systems, security of the keystream generator is
often based on a large inner state rather than an inherently secure design. As a
consequence, an increasing number of attacks on stream ciphers exploit the (re-
)initialisation of large inner states by a weak initialisation function.
In this paper, we propose a strict separation of keystream generator and initialisa-
tion function in stream cipher design. After giving lower bounds on the necessary
inner state size, we show how a secure stream cipher can be constructed from a
weak keystram generator. We introduce the notion of inner state size efficiency
and compare it for a number of fielded stream ciphers, indicating that a secure
cipher can be based on reasonable inner state sizes. Concluding, we ask a number
of open questions that may give rise to a new field of research that is concerned
with the security of initialisation functions.
Keywords: Stream cipher, keystream generator, initialisation, inner state.
1 Introduction
Background: Let m = (m
1
, m
2
, . . .) be a message consisting of blocks m
t
∈ {0, 1}
w
.
A stream cipher is a pair of efficient algorithms, where encryption transforms a message
block m
t
into a ciphertext block c
t
∈ {0, 1}
w
and decryption implements the inverse
transformation. Both encryption and decryption run under the control of a key K and
a counter t. Note that the use of a counter is the critical difference between a stream
cipher and a block cipher.
A frequent building block for stream ciphers is a keystream generator, i.e. a finite
state machine that transforms K into a pseudorandom bitstream z = (z
1
, z
2
, . . .) with
z
t
∈ {0, 1}
w
. In most cases, z
t
is added bitwise to m
t
for encryption and to c
t
for
decryption.
While a large body of literature exists on the design of keystream generators (cf.
[33, 27]), the remaining aspects of stream cipher design are less well researched. Only
few guidelines exist for the choice of important parameters like key length, inner state
size, or the number of bits produced before re-keying. The same uncertainty exists with
respect to the key setup algorithm that transforms the key into a starting state for the
generator.
The consequences in practical stream cipher design are twofold. On one hand, an
increasing number of stream ciphers is broken not by attacking the keystream generator,
but by attacking the key setup algorithm (e.g. RC/4 as used in the WEP protocol [35], or
Zenner E. (2004).
On the Role of the Inner State Size in Stream Ciphers.
In Proceedings of the 2nd International Workshop on Security in Information Systems, pages 237-250
DOI: 10.5220/0002676702370250
Copyright
c
SciTePress

A5/1 from the GSM standard [17]). There exist a few general attack techniques against
weak setup functions for stream ciphers (e.g. resynchronisation attacks [13, 23]), but no
design criteria for good initialisation functions. Considering recent research progress
on related key attacks for pseudorandom functions (see [6] and subsequent work), more
problems for stream ciphers designed in an ad-hoc manner are to be expected in the
future.
On the other hand, when a cipher is successfully attacked, a common solution is
to change the parameters while keeping the general design intact. Examples include
increasing the inner state size (e.g. for LILI-128 [9]) or decreasing the security level
(e.g. for Sober-128 [25]). For some ciphers, huge security margins for the parameters
are used in the first place (e.g. more than 33,000 bit of inner state for SEAL [32]).
Paper outline: This paper intends to be a starting point for future research on the design
of stream ciphers. We consider the construction of such ciphers from two primitives:
a keystream generator and an initialisation function. Observe that the inner state of
the cipher forms the interface between those two primitives. While a large inner state
is advantageous for the security of the keystream generator, it makes the task of the
initialisation algorithm more difficult. It also requires more memory, hampering the use
on a restricted computational device like a smart card. In many respects, inner state
bits are to stream ciphers what encryption rounds are to block ciphers: Given a large
number of them, almost any design can be secure while at the same time, performance
is suffering.
Our goal is to improve the understanding of the necessity and the limitations of the
inner state. To this purpose, in section 2, we introduce a formal model of the stream
ciphers considered. In section 3, we discuss the cryptographic relevance of inner states,
giving lower bounds on the minimum size as well as a construction for a secure stream
cipher when inner state size and initialisation time are not critical. In section 4, we
observe that the inner state size has to be limited in most practical stream ciphers. This
leads us to the definition of inner state efficiency, yielding a measure of how much the
inner state size actually contributes to the security of the keystream generator. We also
give concrete values of inner state efficiency for a number of practical stream ciphers.
Concluding, in section 5, our results are summarised, and a list of open questions for
future research on stream cipher design is presented.
2 Terminology
2.1 Keystream generators
Basic model: In [33], Rueppel defined a
keystream generator
as consisting of the fol-
lowing components (see the box in figure 1):
(a) An inner state S
t
∈ S with S ⊆ {0, 1}
n
,
(b) an update function f : S → S that modifies the inner state with each clock, and
(c) an output function g : {0, 1}
v
→ {0, 1}
w
, w ≤ v ≤ n, that uses the inner state to
compute w keystream bits with each clock.
(d) a Boolean predicates C : S → {0, 1}, such that an inner state S is a valid starting
state iff C(S) = 1.
238
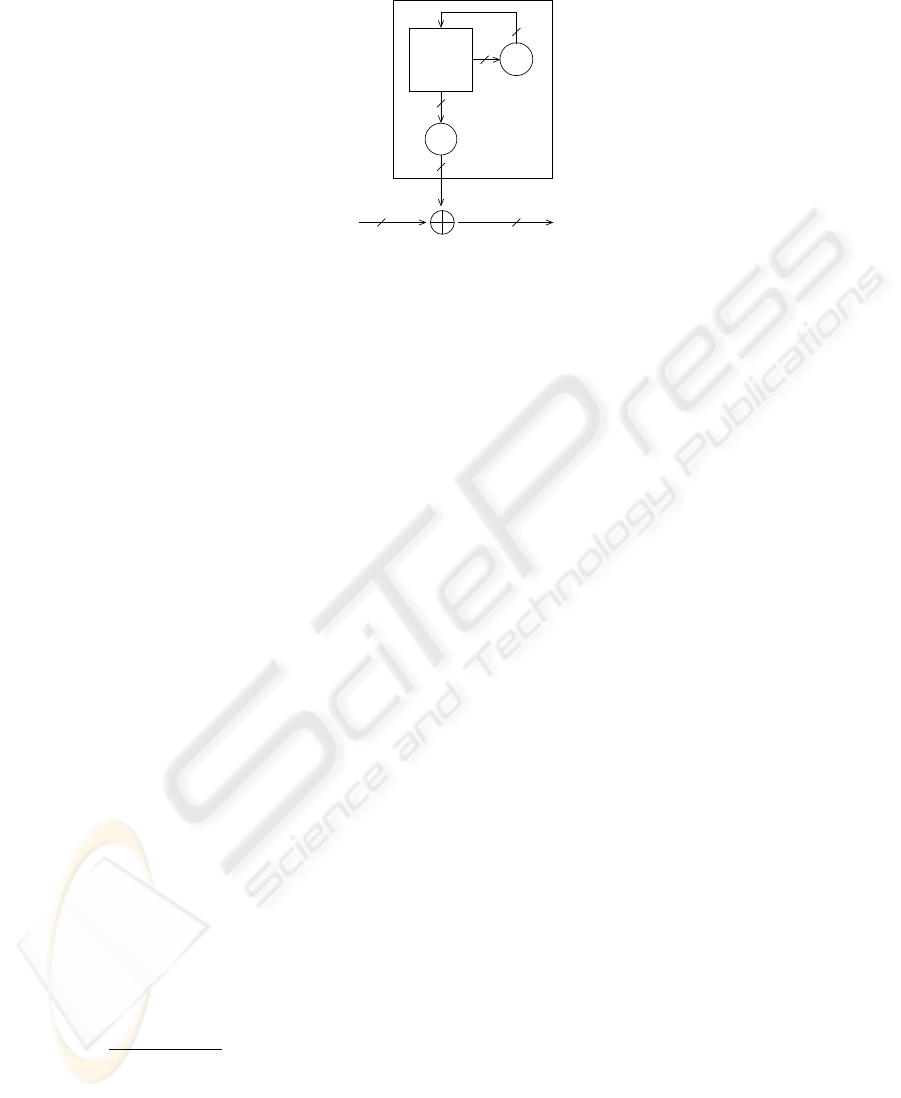
g
f
t
z
t
S
t t
cm
w w
w
v
n
n
Fig. 1. General model of a keystream generator
Deployment in stream ciphers: Keystream generators are often used in cryptography to
implement efficient stream ciphers. A wide-spread design requires the following addi-
tional components:
(A) A secret
key
K ∈ {0, 1}
l
that is not necessarily identical to the inner state,
(B) an
initialisation function
h : {0, 1}
l
× {0, 1}
m
→ S that derives a starting state
S
0
from the key K and m bit of additional information (like an initial value or a
nonce), such that C(S
0
) = 1.
(C) the
xor-function
⊕ : {0, 1}
w
× {0, 1}
w
→ {0, 1}
w
which adds the keystream
bitwise modulo 2 to the plaintext, generating the ciphertext
1
.
2.2 Inner state size:
A na
¨
ıve candidate for the inner state size is the parameter n, denoting the length of
the inner state representation. There is, however, the obvious problem that the same
generator may be represented in different ways, yielding different values of n depending
on the concrete implementation.
Instead, in order to derive a unique definition of the inner state size, we consider an
autonomous finite state machine
(AFSM) implementing the generator
2
. Such an AFSM
consists of a set S of inner states, and for each inner state S ∈ S, there exists
– a
transition rule
that defines the next state f(S) for S, and
– a
label
defining the output g(S) generated from S.
In addition, each finite state machine needs a set S
0
of valid
starting states
.
Note that there exists an infinite number of AFSM describing the generator. In par-
ticular, the size of the AFSM (i.e. the number of inner states) can vary arbitrarily. Thus,
in order to find a unique value for the number of inner states, we need to revert to the
notion of the
minimal AFSM
describing the generator.
1
In fact, other functions like addition modulo 2
w
are also possible, but rarely used.
2
For a full discussion of this topic, cf. [37]
239

An AFSM is said to
generate
an (infinite) output sequence z = (z
0
, z
1
, . . .) if there
exists a starting state S
0
∈ S
0
such that z
i
= g(f
i
(S
0
)). Two AFSM A and B are
said to be
equivalent
if all (infinite) output sequences produced by A are also produced
by B, and vice versa. As a consequence, all AFSM that describe a given keystream
generator are equivalent. An AFSM is said to be
minimal
if no equivalent AFSM of
smaller size exists. Thus, if a minimal AFSM for a given generator can be found, its
size yields the minimal number of inner states required to implement the generator.
Having introduced these notions, we can define the unique inner state size of the
generator as follows:
Definition 1. Let G be a keystream generator as defined above, and let A be a minimal
AFSM implementing G. Then the inner state size of the generator G is defined as ˆn :=
dlog
2
(|A|)e, where |A| is the number of inner states of A.
2.3 Attacker model
Prior knowledge: The attacker is assumed to know everything about the stream cipher
with the exception of the key K and the current inner state S
t
. In particular, he is aware
of the set S of possible inner states and of the functions f, g and h. He also knows (or
even controls) the m bit of public information that are used, along with the key, to set
up the inner state S
0
.
Class of attack: We consider a known-plaintext attack. Since knowledge of plaintext
and ciphertext implies knowledge of the keystream, it can be assumed that the attacker
has L ¿ 2
l
known keystream bits at his disposal.
Computational resources: The attacker can do any computation that requires less steps
than a complete search over the key space. This bound holds both for the precomputa-
tion and the actual attack phase, implying a bound of strictly less than 2
l
bits of memory
that can be used.
Notion of success: An attacker is considered successful if he can correctly predict
previously unknown keystream bits, or if he can distinguish the output of the keystream
generator from truly random bits. We say that the keystream generator is broken if there
exists an attacker whose success probability differs significantly from pure guessing.
Note that in particular, reconstruction of a correct tupel (t, S
t
) or of the key K implies
a successful attack in the above sense.
3 Cryptographic strength from large inner states
3.1 The necessity of large inner states
In the following, let l denote the key length, ˆn the inner state size and n the length of the
inner state representation (n ≥ ˆn). For most practical stream ciphers, it can be observed
that n > l holds. We will briefly discuss that this is in fact a necessary condition for
secure stream ciphers.
240

First lower bound: The main design goals of practical stream ciphers are security and
efficiency. In order to achieve the efficiency goal, the functions f, g and h are chosen to
be as simple as possible. In particular, g : {0, 1}
v
→ {0, 1}
w
is constructed such that
w ≤ v < min{l, n}.
Lemma 1. Let the output function g depend on v < l inner state bits and let the output
be balanced. Then the keystream generator can not be secure if n < l + w.
Proof. For such a generator, a divide-and-conquer attack can be mounted: The attacker
guesses all v bits of the inner state representation that are input to g (since v < l, this
is feasible in our attack model). He then verifies whether the output of g matches the
observed value z
0
. Since g is balanced, only 2
−w
of all assignments meet this criterion,
strongly reducing the search space. The attacker can now mount a complete search over
the remaining assignments, yielding an attack in 2
n−w
steps. If n < l + w, this attack
would be more efficient than brute force search over the key space of the stream cipher.
2
Since the value n depends on the implementation and is thus not under the control of the
cipher designer, the inner state size must be chosen such that the above attack becomes
infeasible for all implementations.
Corollary 1. If v < l, a necessary condition for a secure keystream generator is ˆn ≥
l + w.
Note that for many ciphers, this attack can be extended using a backtracking approach
[21, 38, 36], yielding an even greater lower bound on the minimum size of the inner
state.
Second lower bound: The requirement for a large inner state gets even stronger if the
attacker has a large amount of keystream bits at his disposal. In this case, time-memory-
data tradeoff attacks have to be taken into account, as follows.
Lemma 2. Let L be the number of keystream bits available to the attacker. Then the
keystream generator can not be secure if n < l + log(L).
Proof. A general time-memory-data tradeoff [3, 21, 7] for w = 1 can be conducted as
follows:
–
Precomputation phase:
The attacker draws a large sample (say, 2
l−²
) of inner states
at random from S. For each sample state S
i
, the generator is run to produce an l-bit
output z
i
. The tuple (z
i
, S
i
) is stored in a table, indexed by z
i
.
–
Attack phase:
The attacker segments the known output stream into roughly L over-
lapping frames ˜z
j
of l bits
3
. For each frame, he checks whether ˜z
j
is contained in
the table, and if yes, he extracts the inner state S.
3
To be exact, there are L − l + 1 such frames.
241

By the birthday paradox, there is high probability for a collision between the set of
samples z
i
in the table and the set of observations ˜z
j
in the keystream if 2
l−²
· L ≈ 2
n
.
Since this attack requires 2
l−²
precomputations and L table-lookups, it is feasible for
the attacker if n ≈ l + log(L) − ², where ² is small.
Note that this proof can be generalised for arbitrary values of w by using frame lengths
that are multiples of w, yielding the same result. 2
Again, the cipher designer can not control n, but only the inner state size ˆn. Remem-
bering that an attacker who is restricted to 2
l
operations can read at most L = 2
l
output
bits, we obtain the following lower bound:
Corollary 2. If the generator produces arbitrarily large output streams, a necessary
condition for a secure keystream generator is ˆn ≥ 2l.
3.2 A generic construction
We have seen that for efficient and secure stream ciphers, the inner state size ˆn must be
strictly larger than the key size l. An obvious question is: What happens if we increase
ˆn further? An interesting observation is that a large inner state can be used to make up
for the deficiencies of a relatively weak keystream generator.
Constructing the stream cipher: Let H = {H
n
| n ∈ N} be a family of cryptograph-
ically secure hash functions H
n
: {0, 1}
∗
→ {0, 1}
n
. Let G = {G
n
| n ∈ N} be a
family of keystream generators with n = ˆn.
4
Furthermore, let the generator be such
that the mapping from state space to the first n keystream bits is bijective. Finally, we
assume that there exists a known parameter c, 0 < c < 1, such that for any generator
G
n
∈ G and given n bits of output stream, predicting additional output bits will require
at least 2
cn
computational steps for all but O(1) cases.
Given these building blocks, we can construct a stream cipher with security level l
as follows. First, choose n such that c · n > l, and use G
n
as keystream generator. The
n bits of inner state for generator G
n
are initialised using the matching hash function
H
n
: {0, 1}
l
× {0, 1}
m
→ {0, 1}
n
.
Security against inversion: It can be shown that such a stream cipher is secure against
inversion attacks, as long as no assumption about G
n
and H
n
is violated.
Lemma 3. If the stream cipher (G
n
, H
n
) can be inverted in less than 2
l
steps, then the
hash function H
n
can be inverted in less than 2
l
+ n steps.
Proof. Assume that there exists an attacker A who, given the description of (G
n
, H
n
)
and at least n bit of cipher output z, can invert the stream cipher in less than 2
l
steps.
Then we can construct an inverter A
0
who, given a valid output y of the hash function
H
n
, finds a corresponding input x such that H
n
(x) = y.
4
Many keystream generators are of that kind, e.g. many LFSR-based combination and filter
generators or clock-controlled generators.
242

– A
0
runs the keystream generator on inner state representation y, producing n bit of
cipher output z = G
n
(y).
– A
0
invokes attacker A with input z and obtains a key k with G
n
(H
n
(k)) = z.
– A
0
outputs k.
Note that k meets the condition G
n
(H
n
(k)) = z. Since G
n
is injective, there exists
only one intermediate value y with G
n
(y) = z, implying that H
n
(k) = y. Thus, A
0
has
inverted the hash function, using 2
l
+ n computational steps. 2
Security against prediction: Analogously, it can be shown that the stream cipher is
secure against prediction attacks, as long as the output of keystream generator G
n
can
not be predicted in less than 2
cn
computational steps in all but a small number of cases.
Lemma 4. If the stream cipher (G
n
, H
n
) can be predicted in less than 2
l
steps, then
the keystream generator G
n
can be predicted in less than 2
l
steps on a significant subset
of its inputs.
Proof. Assume that there exists an attacker A who, given the description of (G
n
, H
n
)
and output bits (z
0
, . . . , z
n−1
), can predict output bits (z
n
, . . . , z
n+d−1
) correctly in
less than 2
l
steps. Then we can construct a trivial predictor A
0
who, given a valid output
(z
0
, . . . , z
n−1
) of G
n
, can predict the subsequent output bits (z
n
, . . . , z
n+d−1
) in at
least 2
l
different cases.
– A
0
runs A on input (z
0
, . . . , z
n−1
) and obtains bits (z
n
, . . . , z
n+d−1
).
– A
0
outputs (z
n
, . . . , z
n+d−1
).
Note that due to the injectivity of G
n
, (z
0
, . . . , z
n−1
) was generated from a unique
starting state S
0
. For the analysis, we have to distinguish two cases:
(a) If S
0
is a possible output of H
n
, the sequence (z
0
, . . . , z
n−1
) is a correct output of
the stream cipher (G
n
, H
n
). Thus, if A predicts correctly for the stream cipher, A
0
predicts correctly for the generator.
(b) If, however, no key k exists such that H
n
(k) = S
0
, the behaviour of A (and thus of
A
0
) is undefined - the prediction may or may not be correct.
In any case, the running time of A
0
is identical to the running time of A, yielding an
effort of less than 2
l
steps. Note that the algorithm is always right if case (a) occurs,
yielding a correct prediction in at least 2
l
(out of 2
n
) cases. 2
4 Inner state efficiency
4.1 Disadvantages of large inner states
In practice, stream ciphers often use a relatively weak keystream generator and rely on
the inner state size and the key schedule algorithm for security. Since constructing a
cipher in the above way is tempting, why not use it as a general design rule?
With all their advantages as demonstrated in sections 3.1 and 3.2, there are also three
arguments against large inner states. The first (and most obvious) one is that memory
243

is not for free. While on a modern PC, sufficient memory should be available, other
platforms like encryption hardware or smartcards may require a more economical use
of resources. A second problem is that cryptographic memory must be protected from
observation (both on general purpose and specialised hardware), and that an increase in
memory size increases the options of an attacker, e.g. for side-channel attacks.
But there is third, more subtle reason why large inner states do not only provide
advantages: most practical stream ciphers have to be re-initialised on a regular basis;
i.e. after producing a fixed number of output bits, a new inner state is computed from
the same key K, but with different additional information. This can be for synchroni-
sation purposes, but also due to cryptographical reasons.
5
However, for a stream cipher
with a large inner state, either performance or security of the initialisation procedure is
impaired.
6
If the cipher re-initialises rather often, the function h must be computable
in as few computational steps as possible. On the other hand, a good mixing of key
and nonce into the starting state can not be obtained in a small number of computa-
tional steps. The lack of widely accepted design criteria for such initialisation functions
further complicates the problem.
4.2 Efficient inner state size
For all of the above reasons, the inner state size must not be too large, even though
a certain minimum size for the inner state is necessary, as shown in subsection 3.1.
Note that the lower bound on the required inner state size depends on the quality of
the keystream generator. In order to make comparisons between different generators
possible, we introduce a measure of inner state efficiency, much in analogy to the well-
known efficient key size.
Definition 2. Let G be a keystream generator, and let A be the best known attack
against G. The
efficient inner state size
of G is a number σ ∈ R such that execut-
ing A takes as many computational steps as a brute force search over 2
σ
starting states
of G. The quotient γ = σ/ˆn is denoted as the
inner state efficiency
and is a measure
for the quality of the keystream generator G.
4.3 Comparison of fielded stream ciphers
For an arbitrary generator, the inner state efficiency lies in the range of 0 ≤ γ ≤ 1.
However, using the time-memory-data tradeoff technique presented in subsection 3.1,
it can be shown that for a generator that produces at least 2
ˆn/2
output bits, the inner
state efficiency is restricted to 0 ≤ γ ≤ 0.5. But what values of γ are encountered in
practice?
In table 1, the efficiency δ of inner states is compared for a number of contemporary
stream ciphers. We denote by l
max
the maximum key length of the overall stream cipher.
5
Note that once the number of keystream bits available to the attacker gets large, most keystream
generators become vulnerable to a wide range of cryptanalytic techniques, like time-memory-
data tradeoffs, correlation attacks, differential attacks, or algebraic attacks.
6
This line of research was first proposed to us by W. Meier [31].
244

Cipher
l
max
ˆn σ γ
A5/1 [8]
64 64 32.0 0.5000
Lili-128 [14]
128 128 48.0 0.3750
E
0
[1]
128 132 49.0 0.3712
Sober-t32 [26]
256 576 158.0 0.2743
SNOW 1.0 [15]
256 576 100.0 0.1736
Scream [24]
128 4,116 100.0 0.0243
RC4 (8bit) [29]
256 1,700 30.6 0.0180
Leviathan [30]
256 6,784 39.0 0.0057
Seal 3.0 [32]
160 33,036 43.0 0.0013
Table 1. Keystream generators of fielded stream ciphers (details: appendix A)
Note that σ represents the most efficient attack that (a) has been published at the moment
and that (b) targets the keystream generator only. Also note that runtime estimates for
cryptographic attacks are always somewhat tricky, but the order of magnitude should
be correct. In appendix A, a short description is given on how values ˆn and σ have been
derived.
It can be observed that the stream ciphers with particularly large internal states have
very low inner state efficiencies. It could be argued that the attacks that determined σ
for these ciphers are distinguishing attacks, and that in all cases, it is not known how to
transform them into prediction or key reconstruction algorithms.
7
But then again, dis-
tinguishing attacks could be mounted against the ciphers with smaller inner states, too,
with less drastic results. As a consequence, the ciphers with large inner states do not
seem to enjoy a real advantage over ciphers with small values for ˆn. In other words: It
should be possible to construct a secure stream cipher from a generator with a reason-
able inner state size.
5 Conclusions and research directions
Directions for future research: The following is an incomplete list of open questions
that might be of interest for a more thorough understanding of stream cipher design.
– How much inner state is required to make a stream cipher secure?
– What is the right cryptographic primitive for a key schedule algorithm? Is a full-
scale pseudorandom function generator required, or can we get away with a less
strict security requirement?
– What constructions for provably secure stream ciphers can be given, in particular
in the concrete security setting [5]?
– Can a set of practical design guidelines for key schedule algorithms be developed,
in analogy to the design guidelines for block ciphers or keystream generators? What
7
In addition, these ciphers are not meant to be re-synchronised frequently. Thus, they can indeed
afford larger internal states under running time considerations, since re-initialisation is required
only rarely.
245

knowledge about key schedule algorithms from block ciphers can be re-used for
stream cipher initialisation?
– What are the conditions for a direct attack on the key? What can be said about the
relationship between the keystream generator and the key schedule? Is it possible to
develop a good stream cipher by using generic keystream generators and key setup
algorithms independently? Or should both algorithms be chosen in an orthogonal
way, being dependent on one another?
Summary: We have have shown that for a wide-spread type of stream ciphers, an in-
crease in inner state size can increase the security of the keystream generator used, but
at the same time can slow down or even weaken the initialisation function. As a conse-
quence, we propose to evaluate the strength of the keystream generator used relative to
its inner state size. To this end, the notion of
inner state efficiency
was introduced. In an
ad-hoc survey of practical stream ciphers, ciphers with large inner states displayed no
cryptographical advantage over those with small inner states. This is an indication that
efficient use of inner states is not just a theoretical claim, but is feasible in practice. To
this end, we gave a number of questions that may be addressed by future research.
Acknowledgements
The author wishes to thank Frederik Armknecht, Stefan Lucks, Willi Meier, and Greg
Rose for encouragement and inspiring discussions.
References
1. Bluetooth Specification v1.1, 1999. www.bluetooth.com.
2. F. Armknecht and M. Krause. Algebraic attacks on combiners with memory. In D. Boneh,
editor, Proc. Crypto 2003, volume 2729 of LNCS, pages 162–175. Springer, 2003.
3. S. Babbage. A space/time tradeoff in exhaustive search attacks on stream ciphers. In Eu-
ropean Convention on Security and Detection, volume 408 of IEE Conference Publication,
May 1995.
4. S. Babbage, C. De Canni
`
ere, J. Lano, B. Preneel, and J. Vandewalle. Cryptanalysis of Sober-
t32. In T. Johansson, editor, Proc. Fast Software Encryption 2003, volume 2887 of LNCS,
pages 111–128. Springer, 2003.
5. M. Bellare. Practice-oriented provable security. In I. Damg
˚
ard, editor, Lectures on Data
Security, volume 1561 of LNCS, pages 1–15. Springer, 1999.
6. E. Biham. New types of cryptanalytic attacks using related keys. In T. Helleseth, editor,
Proc. Eurocrypt ’93, volume 765 of LNCS, pages 398–409. Springer, 1993.
7. A. Biryukov and A. Shamir. Cryptanalytic time/memory/data tradeoffs for stream ciphers.
In T. Okamoto, editor, Proc. Asiacrypt 2000, volume 1976 of LNCS, pages 1–13. Springer,
2000.
8. M. Briceno, I. Goldberg, and D. Wagner. A pedagogical implementation of A5/1.
http://www.scard.org/gsm/a51.html.
9. A. Clark, E. Dawson, J. Fuller, H.-J. Lee J. Dj. Goli
´
c, W. Millan, S.-J. Moon, and L. Simpson.
The LILI-II keystream generator. In L. Batten and J. Seberry, editors, Proc. ACISP 2002,
volume 2384 of LNCS, pages 25–39. Springer, 2002.
246

10. D. Coppersmith, S. Halevi, and C. Jutla. Cryptanalysis of stream ciphers with linear masking.
In M. Yung, editor, Proc. Crypto 2002, volume 2442 of LNCS, pages 515–532. Springer,
2002.
11. N. Courtois. Fast algebraic attacks on stream ciphers with linear feedback. In D. Boneh,
editor, Proc. Crypto 2003, volume 2729 of LNCS, pages 176–194. Springer, 2003.
12. P. Crowley and S. Lucks. Bias in the LEVIATHAN stream cipher. In M. Matsui, editor, Proc.
Fast Software Encryption 2001, volume 2355 of LNCS, pages 211–218. Springer, 2002.
13. J. Daemen, R. Govaerts, and J. Vandewalle. Resynchronisation weakness in synchronous
stream ciphers. In T. Helleseth, editor, Proc. Eurocrypt ’93, volume 765 of LNCS, pages
159–167. Springer, 1994.
14. E. Dawson, A. Clark, J. Goli
´
c, W. Millan, L. Penna, and L. Simpson. The LILI-128
keystream generator.
http://www.isrc.qut.edu.au/resource/lili/
lili
nessie
workshop.pdf.
15. P. Ekdahl and T. Johansson. SNOW - a new stream cipher.
http://www.it.lth.se/cryptology/snow/. NESSIE project submission.
16. P. Ekdahl and T. Johansson. A new version of the stream cipher SNOW. In H. Heys and
K. Nyberg, editors, Proc. SAC 2002, volume 2595 of LNCS, pages 47–61. Springer, 2002.
17. P. Ekdahl and T. Johansson. Another attack on A5/1. IEEE Trans. Information Theory,
49(1):284–289, 2003.
18. H. Finney. An RC4 cycle that can’t happen. Newsgroup post to sci.crypt, September 1994.
19. S. Fluhrer. Cryptanalysis of the SEAL 3.0 pseudorandom function family. In M. Matsui, ed-
itor, Proc. Fast Software Encryption 2001, volume 2355 of LNCS, pages 135–143. Springer,
2002.
20. S. Fluhrer and D. McGrew. Statistical analysis of the alleged RC4 keystream generator.
In B. Schneier, editor, Proc. Fast Software Encryption 2000, volume 1978 of LNCS, pages
19–30. Springer, 2001.
21. J. Goli
´
c. Cryptanalysis of alleged A5 stream cipher. In W. Fumy, editor, Proc. Eurocrypt
’97, volume 1233 of LNCS, pages 239–255. Springer, 1997.
22. J. Goli
´
c. Linear statistical weakness of alleged RC4 keystream generator. In W. Fumy, editor,
Proc. Eurocrypt ’97, volume 1233 of LNCS, pages 226–238. Springer, 1997.
23. J. Goli
´
c and G. Morgari. On the resynchronization attack. In T. Johansson, editor, Proc. Fast
Software Encryption 2003, volume 2887 of LNCS, pages 100–110. Springer, 2003.
24. S. Halevi, D. Coppersmith, and C. Jutla. Scream: A software-efficient stream cipher. In
J. Daemen and V. Rijmen, editors, Proc. Fast Software Encryption 2002, volume 2365 of
LNCS, pages 195–209. Springer, 2002.
25. P. Hawkes and G. Rose. Primitive specification for Sober-128.
http://www.qualcomm.com.au/Sober128.html.
26. P. Hawkes and G. Rose. Primitive specification and supporting documentation for Sober-t32.
NESSIE project submission, October 2000.
27. S. Jiang and G. Gong. Cryptanalysis of stream cipher - a survey. Technical Report CORR-
2002-29, University of Waterloo, 2002.
28. T. Johansson and A. Maximov. A linear distinguishing algorithm on Scream. Presented at
ISIT 2003, available at
http://www.it.lth.se/movax/Publications/2003/Scream/
disting.pdf.
29. Itsik Mantin. Analysis of the stream cipher RC4. Master’s thesis, Weizmann Institute of
Science, Rehovot, Israel, November 2001.
30. D. McGrew and S. Fluhrer. The stream cipher Leviathan. NESSIE project submission,
October 2000.
247

31. W. Meier. personal communication, August 2003.
32. P. Rogaway and D. Coppersmith. A software-optimized encryption algorithm. Journal of
Cryptology, 11(4):273–287, Fall 1998.
33. R. Rueppel. Stream ciphers. In G. Simmons, editor, Contemporary Cryptology - The Science
of Information Integrity, pages 65–134. IEEE Press, 1992.
34. M.-J. Saarinen. A time-memory tradeoff attack against LILI-128. In J. Daemen and V. Rij-
men, editors, Proc. Fast Software Encryption 2002, volume 2365 of LNCS, pages 231–236.
Springer, 2002.
35. A. Stubblefield, J. Ioannidis, and A. Rubin. Using the Fluhrer, Mantin and Shamir attack to
break WEP. Technical Report TD-4ZCPZZ, AT&T labs, August 2001.
36. E. Zenner. On the efficiency of clock control guessing. In P. J. Lee and C. H. Lim, editors,
Proc. ICISC ’02, volume 2587 of LNCS, pages 200–212. Springer, 2003.
37. E. Zenner. On the role of the inner state size in stream ciphers. Technical Report Informatik
TR-04-001, University of Mannheim (Germany), January 2004. available at
http://www.informatik.uni-mannheim.de/techberichte/
html/TR-04-001.html.
38. E. Zenner, M. Krause, and S. Lucks. Improved cryptanalysis of the self-shrinking generator.
In V. Varadharajan and Y. Mu, editors, Proc. ACISP ’01, volume 2119 of LNCS, pages 21–35.
Springer, 2001.
A Deriving ˆn and σ
In the following, the inner states and best known attacks for the keystream generators in
section 4.3 are discussed. In most cases, inner states can be subdivided into a linear part
(i.e. inner states whose update function is linear), a nonlinear part, and key-dependent
S-boxes which may or may not be bijective.
Note that for each stream cipher, only those attacks that target the keystream gener-
ator directly are considered.
–
A5/1:
The inner state is purely linear, consisting of 64 bit.
Numerous attacks have been proposed against the full A5/1 stream cipher, all taking
into account that in practice, only a small number of output bits is available to the
attacker. If, however, we assume an arbitrary amount of output bits, the generic
time-memory-tradeoff attack is most efficient, yielding σ = 32.
–
E
0
:
The inner state consists of a 128-bit linear part and a 4-bit nonlinear part.
A number of attacks against the E
0
generator have been proposed in literature.
For the time being, the algebraic attack technique proposed by Courtois [11] using
equations developed by Armknecht and Krause [2] seems to be the most efficient,
requiring roughly 2
49
computational steps. The attack does, however, require more
consecutive output bits than the cipher produces between two re-initialisations.
–
Leviathan:
The inner state consists of a 48-bit counter and 4 permutation tables
over {0, 1}
8
. Thus, the overall inner state size is 16 + 4 · 1, 684 = 6, 784 bit.
The best known attack against Leviathan is a distinguisher by Crowley and Lucks
[12], requiring 2
39
bits of output and a similar work effort.
–
LILI-128:
The inner state consists of two independent linear states of sizes 39 and
89 bit, respectively, yielding a total inner state size of 128 bit.
Given the construction of the cipher, a security level of 128 bit was not achievable
248

in the first place due to lemma 1. As a consequence, a number of attacks on LILI-
128 have been published, the most efficient one being a specialised time-memory
attack by Saarinen [34] that requires roughly 2
48
computational steps. Note that the
attack proposed by Courtois in [11] formally requires less computational steps, but
needs 2
60
output bits.
In the meantime, a successor LILI-II has been published [9]. The inner state size
has been almost doubled to 255 bits, with the allowed key size still at 128 bit. No
cryptanalysis of LILI-II has been published so far.
–
RC4 (8-bit version):
The inner state size of RC4 is difficult to analyse. It consists
of two 8-bit state variables and a table that implements a permutation {0, 1}
8
that
changes over time. Normally, this would yield an inner state size of 16 + 1, 684 =
1, 700 bit. However, the starting values for the state variables are key-independent,
and it was shown by Finney [18] that a fraction of 1/256 states can never be
reached. Experiments on smaller versions of RC4 seem to indicate that the frac-
tion of non-reachable states is even larger but still small enough that 1, 700 is a
good approximation of the inner state size.
Numerous attacks against RC4 have been described. A particularly strong attack
against its keystream generator was proposed by Goli
´
c [22] and improved by Fluhrer
and McGrew [20]. The attack is a distinguisher that requires 2
30.6
output bits and a
similar amount of work.
–
Scream:
The generator uses an evolving state of 128 bit, a round key of 256 bit,
a mask table (16 times 16 bytes) of 2,048 bit, and an S-Box that implements a
permutation over {0, 1}
8
(1,684 bit). Thus, the inner state size is 4,116 bit.
The best attack against Scream that we are aware of is a linear distinguisher by
Johansson and Maximov [28]. It requires about 2
100
output bits and a similar work
effort. Note, however, that Scream has been published only quite recently, i.e. it has
not yet received the full cryptanalytic consideration.
–
Seal 3.0:
The generator uses a 12 bit counter, 8 32-bit state words, and a set of
lookup tables consisting of 1024 32-bit words, contributing up to 32, 768 bit to the
inner state. Thus, the inner state size of the generator is 33, 036 bit.
While the state words are re-initialised every 2
6
· 2
7
= 2
13
output bits, the ta-
bles are re-initialised once every 2
19
output bits. Thus, SEAL has two initialisation
functions h
1
and h
2
, and can be seen considered as a stream cipher (H, G) =
((h
1
, h
2
), g). Note that the best known attack - a distinguishing attack by Fluhrer
[19] that requires rougly 2
43
computational steps - is only applicable if (h
2
, g) is
considered as the keystream generator.
8
–
Snow 1.0:
The linear part contributes 16 32-bit words to the inner state, while the
nonlinear part adds another 2 32-bit words, yielding a total inner state size of 576
bit.
Amongst the attacks proposed against Snow 1.0, the most efficient is a distinguisher
by Coppersmith et al. [10], requiring about 2
100
computational steps.
An updated version Snow 2.0 with equal inner state size has been proposed [16],
but no cryptanalytic results are available yet.
8
The inner generator g is in fact a one-time pad: Without additional knowledge about the ini-
tialisation function, it is secure in an information-theoretical sense.
249

–
Sober-t32:
Here, the inner state consists of 17 linear 32-bit words and one 32-bit
constant. Thus, the inner state size is 576 bit.
The most efficient attack against full Sober-t32 is a distinguisher presented by Bab-
bage et al. [4], requiring 2
153+5
= 2
158
output bits and a similar work effort.
Recently, a new version Sober-128 with equal inner state size but reduced key
length was published [25]. However, no cryptanalytic results are available for the
time being.
250
