
METHOD FOR ALARM PREDICTION
Luis Pastor Sanchez Fernandez
Center for Computing Research. Mexico City, Mexico.
Lazaro Gorostiaga Canepa
Center of Automatization, Robotics and Technologies of the Information and the Manufacture. Spain
Oleksiy Pogrebnyak
Center for Computing Research. Mexico City, Mexico.
Keywords: Alarm, prediction, supervision, trend, identification, neural networks.
Abstract: The goal of this paper is to show a predictive supervisory method for the trending of variables of
technological processes and devices. The data obtained in real time for each variable are used to estimate the
parameters of a mathematical model. This model is continuous and of first-order or second-order (critically
damped, overdamped or underdamped), all of which show time delay. An optimization algorithm is used for
estimating the parameters. Before performing the estimation, the most appropriate model is determined by
means of a backpropagation neural network (NN) previously trained. Virtual Instrumentation was used for
the method programming.
1 INTRODUCTION
The antecedents are methods for supervising
technological processes (Juricek, Seborg and
Larimore, 1998) and more specifically, the
algorithms that devices use to detect special or
abnormal conditions. These conditions will be
determined by the values taken up by their variables
in the chosen algorithm. Alarm algorithms by limits
and hysteresis may be used, but they are limited to
diagnose conditions that exist already or that are
likely to occur in a short period of time. This paper
aims at developing more detailed algorithms using
mathematical models representing the dynamics of
the processes that will be supervised. The presented
method makes it possible to predict, in short time,
possible abnormal conditions. This will give rise to
one of two possibilities. The first is a series of
preventative actions to prevent the system from
operating in such a way. The second is a series of
actions for the successful operation of the process
upon reaching the critical state that may or may not
be abnormal (as it happens with hydraulic canals
whose dynamics are complex).
The backpropagation network (NN) was chosen
due to it’s ability to successfully recognize diverse
patterns. In our case, it is used to recognize signal
patterns of first and second order dynamic systems
(Ogata, 2001) in which the dynamics of a
considerable amount of technological processes can
be represented. The methodology used consists of
estimating the parameters of the models through an
optimization algorithm (Edgar and Himmelblau,
1988). Before such parameters are estimated, the
most appropriate model is determined by means of a
NN, thus reducing the total processing time.
A broad range of mathematical techniques,
ranging from statistics to fuzzy logic, have been
used to great advantage in intelligent data analysis
(Robins, 2003).
The following transfer functions are used:
First order model:
-θs
1
Ke
Gm(s) =
Ts+1
(1)
Second order model:
336
Pastor Sanchez Fernandez L., Gorostiaga Canepa L. and Pogrebnyak O. (2005).
METHOD FOR ALARM PREDICTION.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 336-339
DOI: 10.5220/0001163203360339
Copyright
c
SciTePress
-θs
22
Ke
Gm(s) =
s/ω n+2ξ s/ω n+1
(2)
where the parameters to be estimated are:
1
T : time constant; K : gain; : natural oscillation
frequency
;
θ
: time delay.
n
w
ζ: coefficient of damping. ζ<1 (underdamped). ζ=1
(critically damped). ζ>1 (overdamped).
2 BLOCK CHART OF THE
METHOD
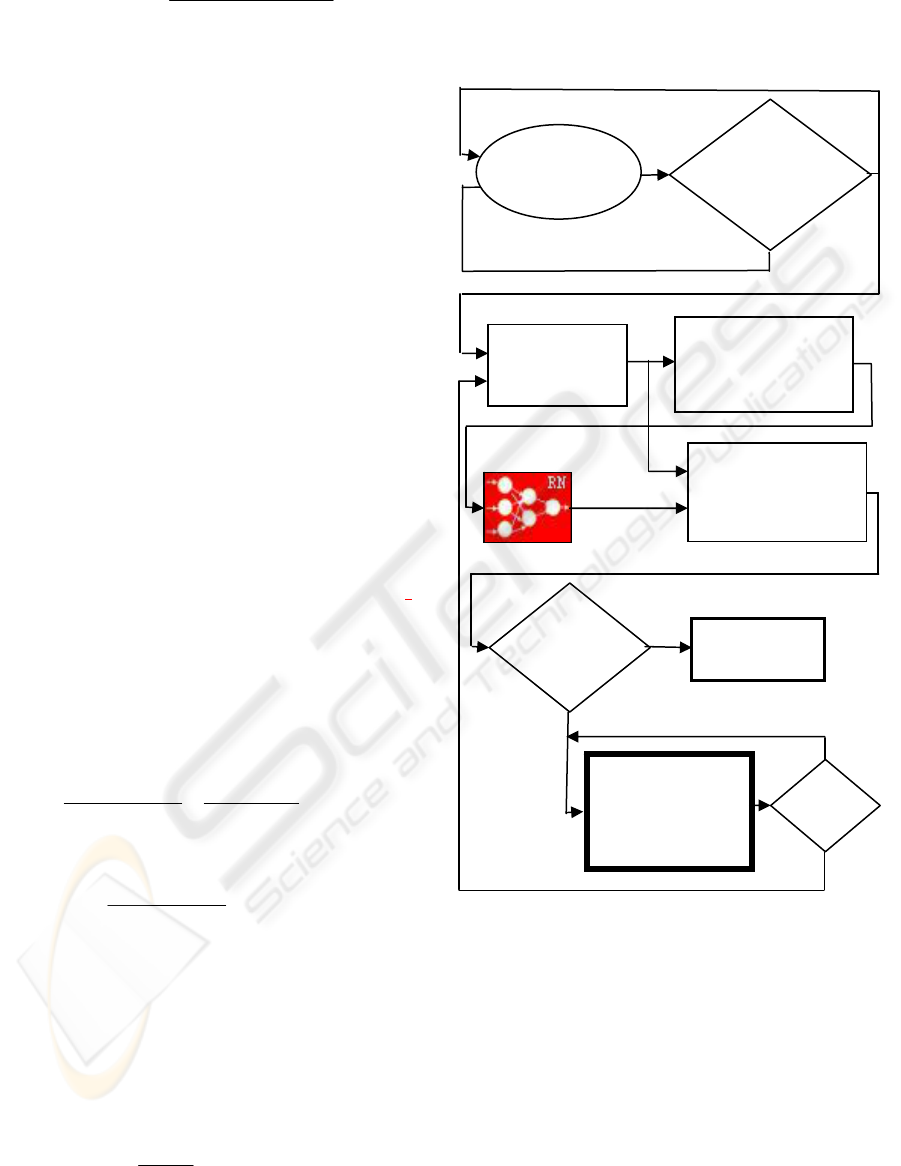
Figure 1 displays the simplified flow chart of a cycle
of the predictive alarm algorithm. A circular buffer
of changeable dimensions is used. This cycle begins
with the permanent storing of N last data of the
variable of the technological process or device under
supervision.
As shown in Figure 2, the instant for
recognizing and estimating the parameters of the
model representing by the points stored in the
circular buffer is determined by an algorithm of
lineal trend prediction. On predicting by lineal trend,
the behavior of the variable is considered to be that
of a straight line from the current sampling instant.
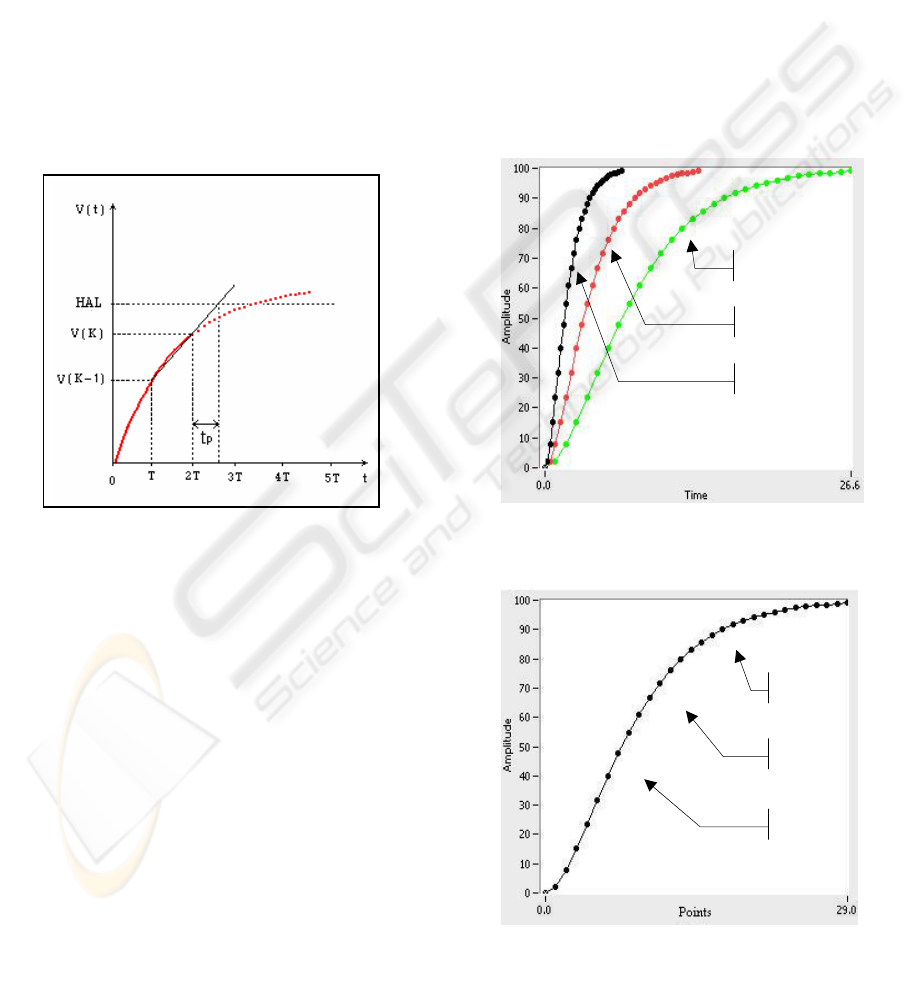
Figure 2 shows an example of a variable versus time
plot V(t) with the following parameters:
HAL: high alarm limit; v(k): current value; v(k-1):
previous value; T: sampling period. The current
sampling instant in this example is 2T.
Regarding Figure 2, it can be stated that:
() ( ) ()
V k -V k-1 LSA-V k
=
2T - T tp
(3)
Obtaining tp as:
() ( )
()
T
tp = LSA - V k
Vk-Vk-1
⎛⎞
⎟
⎜
⎡⎤
⎟
⎜
⎟
⎢⎥
⎜
⎣⎦
⎟
⎜
⎟
⎜
⎟
⎝⎠
(4)
The minimum prediction time T
mp
must be set,
such that if tp < T
mp,
then the recognition process of
the signal pattern represented by the samples stored
in the circular buffer begins.
Afterwards,
digital filtering by the moving
average filter (Oppenheim, Schafer and Buck, 1999)
is performed according to the following expression:
+M
1
Y(k) = X(k -i)
2M +1
i=-M
∑
(5)
where
M = 2 was used.
The latest data are selected if it is the time for
recognizing and estimating the parameters of the
model.
Then, a sampling
frequency conversion with a
non-integer factor combining interpolation and
decimation is performed (Oppenheim, Schafer and
Buck, 1999) which makes it possible to obtain 30
points. This is the number of input neurons of the
NN. Later, the
selection of the weights of the NN is
accomplished in accordance with the sign of the 30-
point-curve slope, since it was trained for the
patterns with a positive and negative slope. As an
output, the NN will produce the most suitable model
with its parameters estimated through an
Figure 1: Flow diagram of the predictive alarm algorithm
cycle
Instant for
recognizing
and estimating
the
p
arameters
Data circular
buffer
No
Yes
•
The latest data
are selected
• Digital filtering.
• Frequency conversion
• Selection of the
weights of the NN
Suitable model
Optimization algorithm
for the fitting of curves
(estimation of the
parameters of the model)
The curve
fitting is
good
No
Yes
•
Prediction by
means of the model
• Prediction error is
calculated (
Pe)
Prediction by
lineal trend
Pe<
ε
Yes
No
METHOD FOR ALARM PREDICTION
337
optimization algorithm for the fitting of curves
using all the selected points
. Hooke and Jeeves´s
(Hooke and Jeeves, 1961) optimization method of
direct search is used. This method returns the
minimized index. If the returned index is smaller
than a value that has been pre-established as fair,
then it is considered that the curve
fitting is good
(estimation of the parameters of the model), and the
prediction by means of the model will be made in
order to predict the time when the variable will
reach its limit value. The algorithm establishes the
value considered as fair for the optimization index
by default. The user can increase or reduce this
value considered as fair if he wants the model to
have more or less accuracy. The
prediction error is
calculated periodically. If the fitting of the model is
not good
, the prediction by lineal trend is made.
2.1 Prediction error
Whenever the prediction is made, an approximate
prediction error (
Pe) is calculated. If this error is
smaller than a pre-established value
ε (Pe<
ε
), the
prediction is continued according to the model;
otherwise, as points keep on being stored in the
circular buffer, another process for estimating
parameters is performed. \
3 NEURAL NETWORK
TRAINING PATTERNS
The selection of the NN training patterns was based
on the behavior of the dynamic responses of first-
and second-order systems to step input function,
because this is the most frequent type of disturbance.
In other cases, even though it might not strictly be an
ideal step, it can be considered as such, provided that
for instance, the time constants of the process are
relatively larger than the time constants of an
exponential signal. Figure 3 displays the responses
of critically damped second order systems, with
natural oscillation frequencies w
n
equal to 1, 0.5 and
0.25 respectively. 30 points are shown for every
curve. They have been taken up from sampling
frequencies of 4, 2 and 1 samples per second,
respectively. That is why every time interval in axis
X will be the sampling period of each curve. If the
points of the three curves were graphically
represented using the same time interval for axis X,
they would be superimposed, as shown in Figure 4.
Figure 3: Responses of critically damped systems
w
n
=1
w
n
=0.5
w
n
=0.25
Figure 4: The three curves of Figure 3, superimposed
Figure 2: Prediction based on the linear-trend of the
variable
w
n
=1
w
n
=0.5
w
n
=0.25
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
338

A similar behavior will occur in first order
systems with respect to the time constant, as well as
in overdamped and underdamped second order
systems, in which only its coefficient of damping
will show any difference.
For NN training patterns, the variations in signal
amplitude are taken up in %, standardized, from
40% to 90%.
After numerous tests, training was carried out
with 858 input patterns, distributed in the following
way:
• For overdamped second order systems (OSO):
For every
ζ value, 11 patterns are obtained
corresponding to the variations of the
amplitude from 40 to 90, with an increase of 5
(40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90).
The
ζ varies from 1.2 to 3, with an increase of
0.09, thus obtaining a total of
220 patterns.
For ζ greater than 3, the behavior of the system
is similar to a first order system.
• For underdamped second-order systems (USO):
As for every
ζ value, 11 patterns corresponding
to amplitude variations are obtained.
The
ζ varies from 0.1 to 0.7, with an increase
of 0.0667, thus obtaining a total of
99
patterns.
• For first- (F) and critically damped second-order
(CSO) systems,
11 patterns are created,
respectively, corresponding to amplitude
variations from 40 to 90.
In order to have a similar number of patterns for
each model and achieve a better training of the NN,
the F and CSO patterns are repeated 20 times,
respectively, for a total of 440 patterns. For the USO
pattern they are repeated twice for 198 patterns. 858
PATTERNS IN ALL.
Once the patterns were chosen, varied topologies
were used until the simplest with the most suitable
response was obtained. Eventually, a 30-input neural
network was used, 11 neurons in the hidden layer
and four-output neurons. Very good results were
obtained in the training and generalization of the
NN. The training error was 0.15%. Over 1000 test
patterns were used, obtaining a correct response,
with an error of 0.9% of failures.
4 CONCLUSIONS AND FUTURE
WORK
Satisfactory results were obtained on training the
neural network, having a high level of
generalization. During the operation, the neural
network recognized the signals used, even those
affected by noise.
The research and the technological advances
presented are a satisfactory step forward in
facilitating the use of advanced and efficient
algorithms of predictive alarm by trend, with
minimum processing time. The presented algorithm
guarantees that the prediction will be corrected in
each period of analysis of the alarm condition states.
This method of predictive alarm has been applied
with good results on several occasions, in managing
hydraulic canals for irrigation and research purposes,
and in controlling sequential processes. For
example, a more efficient operation of a set of tanks
was developed by predicting the time in which a
tank level will reach a limit value.
Moreover, work has began to enhance the neural
network to not only select the most appropriate
model, but also make a pre-estimation of such a
model. This optimization algorithm would be
extremely efficient as its initial operation conditions
would be the values pre-estimated by the neural
network.
REFERENCES
Edgar, T.F. and Himmelblau, D.M., 1988. Optimization of
chemical processes, NY, MacGraw-Hill.
Hooke, R.A. and Jeeves, T.A., 1961. Direct Search
Solution for Numerical and Statistical Problems.
Journal ACM 8, 212-221.
Juricek, B.C., D.E. Seborg and W.E. Larimore, 1998.
"Early Detection of Alarm Situations Using Model
Predictions," Proc. IFAC Workshop on On-Line Fault
Detection and Supervision in the Chemical Process
Industries, Solaize, France.
Ogata, K.. 2001. Modern Control Engineering, 4th
Edition. Prentice Hall, NY.
Oppenheim, A.V., Schafer, R.W. and Buck, J.R., 1999.
Discrete-Time Signal Processing, 2nd Edition.
Prentice-Hall Int. Editions.
Robins, V. et al., 2003. Topology and Intelligent Data,
Advances in Intelligent Data Analysis V, Lecture
Notes in Computer Science, Springer-Verlag GmbH,
Vol. 2810, 275–285
.
METHOD FOR ALARM PREDICTION
339
