
COMPOSITIONAL ANALYSIS FOR REGULARITY, LIVENESS
AND BOUNDEDNESS
Li Jiao
Laboratory of Computer Science, Institute of Software, Chinese Academy of Sciences, Beijing, China
Keywords: Analysis, boundedness, composition, liveness, Petri nets, regularity.
Abstract: By the linear algebraic representation of Petri nets, Desel introduced regularity property (Desel, 1992).
Regularity implies a sufficient condition for a Petri net to be live and bounded. All the conditions checking
the regularity of a Petri net are decidable in polynomial time in the size of a net (Desel and Esparza, 1995).
This paper proves that regularity, liveness and boundedness can be preserved after applying many
compositional operations to Petri nets. This means that, by applying these compositional operations, a
designer can construct complex nets satisfying regularity, liveness and boundedness properties from simpler
ones without forward analysis.
1 INTRODUCTION
As a graphical and mathematical tool, Petri nets
provide a uniform environment for modeling, formal
analysis, and design of discrete event systems. One
of the major advantages of using Petri net models is
that the same model can be used for the analysis of
behavioural properties and performance evaluation,
as well as for systematic construction of discrete-
event simulators and controllers (Zhou and
Venkatesh, 1999).
One net is regular if it satisfies the conditions of
the Rank Theorem described in algebraic methods
(Desel, 1992; Desel and Esparza, 1995). Regularity
is a sufficient condition for ordinary nets to be live
and bounded (Desel and Esparza, 1995). In general,
a system is live if all its operations are eventually
executable, starting not only from its initial state but
also from any reachable state. A system is bounded
if it has a finite number of states. In the terminology
of Petri nets, liveness requires the firability of every
transition starting from any reachable marking,
boundedness implies that the number of tokens
existing in every place will not exceed a certain limit.
For system designs specified in Petri nets, the
major approaches for verification include reach-
ability analysis, direct proving on the basis of
definitions, mathematical programming, characteri-
zation and property-preserving transformation. This
paper relates to the fourth approach, i.e., the
property-preserving transformation. In this approach,
the original net is assumed to satisfy some specific
properties and the transformation is required to
preserve these properties in the transformed net. The
advantage of this approach is that the transformed
net is automatically correct without the need of
forward verification.
Transformations on Petri nets may be roughly
classified into three groups, namely reduction,
refinement and composition. In the literature, there
has been much work related to transformations that
preserve liveness and/or boundedness (Berthelot,
1986; Berthelot, 1987; Esparza, 1994; Koh and
DiCesare, 1991; Suzuki and Murata, 1983; Valette,
1979; Souissi, 1991; Zhou, 1996; Huang, Jiao and
Cheung, 2005). The preservation of regularity has
not been considered. This paper introduces four
kinds of composition operations in terms of places
and transitions. They are: merging two places each
coming from different net; merging two places
coming from the same net; merging two transitions
each coming from different net; merging two
transitions coming from the same net. For each kind
of the four composition operations, this paper proves
that regularity, liveness and boundedness can be
preserved automatically or under some simper
conditions.
This paper is organized as follows: Section 2
presents some basics about Petri nets including
algebraic characterizations. Four compositional
operations in terms of places and transitions are
169
Jiao L. (2005).
COMPOSITIONAL ANALYSIS FOR REGULARITY, LIVENESS AND BOUNDEDNESS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 169-174
DOI: 10.5220/0001178901690174
Copyright
c
SciTePress

introduced and the preservation of regularity is
verified in Sections 3. Section 4 proves that liveness
and boundedness can be preserved under these
operations. In this section, an example is given to
illustrate some results of this paper. Some
concluding remarks are given in Section 5.
2 PRELIMINARIES OF PETRI
NETS
This section outlines the definitions, terminology
and properties as required in the paper.
A net is denoted by N = (P, T, F), where P is a
non-empty finite set of places, T is a non-empty
finite set of transitions with P ∩ T = ∅ and F ⊆ (P ×
T) ∪ (T × P) is a flow relation. The pre-set of x is
defined as
•
x = {y ∈ P ∪ T | (y, x) ∈ F} and the
post-set of x is defined as x
•
= {y ∈ P ∪ T | (x, y) ∈
F}. Similarly, for any subset of Y ⊆ P ∪ T,
•
Y (resp.,
Y
•
) denotes the union of
•
y (resp., y
•
) for all y ∈ Y. A
net N = (P, T, F) is said to be pure or self-loop-free
iff
•
x ∩ x
•
= ∅ ∀x ∈ P ∪ T. We just discuss pure
nets in this paper.
The incidence matrix V of a pure net N is a |P| × |T|
matrix whose element v
ij
at row p
i
and column t
j
is
denoted as follows: v
ij
= 1 if p
i
∈ t
j
•
; v
ij
= -1 if p
i
∈
•
t
j
;
and v
ij
= 0 if p
i
•
•
∪∉
jj
tt
.
A marking of a net N = (P, T, F) is a mapping
M: P → {0, 1, 2, …}. A place p is said to be marked
by M if M(p) > 0. A transition t is enabled or firable
at a marking M if for every p ∈
•
t, M(p) ≥ 1. A
transition t may be fired if it is enabled. Firing
transition t results in changing the marking M to a
new marking M', where M' is obtained by removing
one token from each p ∈
•
t and by putting one token
to every p ∈ t
•
. R(N, M
0
) denotes the set of all
markings reachable from the initial marking M
0
.
A transition t is said to be live in a Petri net (N,
M
0
) iff, for any M ∈ R(N, M
0
), there exists M' ∈
R(N, M) such that t can be fired at M'. (N, M
0
) is said
to be live iff every transition of N is live. A place p
is said to be bounded in (N, M
0
) iff there exists a
constant k such that M(p) ≤ k for all M ∈ R(N, M
0
).
(N, M
0
) is bounded iff every place of N is bounded.
For x ∈ P ∪ T, the cluster of x, denoted as [x],
is the smallest subset of P ∪ T satisfying three
conditions: (1) x ∈ [x]; (2) if p ∈ P ∩ [x] then p
•
⊆
[x]; and (3) if t ∈ T ∩ [x] then
•
t ⊆ [x]. N is said to
satisfy the rank-and-cluster property iff the rank of
its incidence matrix is less than the number of its
clusters by 1.
A net N is said to be connected iff every pair of
nodes (x, y) satisfies (x, y) ∈
∗−
∪ )(
1
FF
. A net N
is said to be strongly connected iff (x, y) ∈
*
F
, i.e.,
there exists a directed path from every node x to
every node y. A P-invariant (resp., T-invariant) of N
is a non-negative integer |P|-vector
α
(resp., |T|-
vector
β
) satisfying the equation
α
V = 0 (resp.,
V
T
β
= 0), where V is the incidence matrix of N. A
P-invariant
α
(resp., T-invariant
β
) of a net is called
semi-positive if
α
≥ 0 and
α
≠ 0 (resp.,
β
≥ 0 and
β
≠
0). The support of a semi-positive P-invariant
α
,
denoted by
〉
〈
α
, is the set of places p satisfying
α
(p)
> 0, and the support of a semi-positive T-invariant
β
,
denoted by
〉
〈
β
, is the set of transition satisfying
β
(t) > 0 (Desel and Esparza, 1995).
A net N is regular (Desel 1992) iff (1) N is
connected, (2) N has a positive P-invariant, (3) N has
a positive T-invariant, and (4) N satisfies the rank-
and-cluster property.
In N, a non-empty set of places D is said to be a
siphon (resp., trap) iff
•
D ⊆ D
•
(resp., D
•
⊆
•
D). A
siphon (resp., trap) is said to be minimal if it does
not properly contain any other siphon (resp., trap).
For more details, please refer to (Recalde,
Teruel and Silva, 1998; Silva, Teruel and Colom,
1998).
3 FOUR COMPOSITIONAL
OPERATIONS AND THE
PRESERVATION OF
REGULARITY
This section considers four compositional operations
in terms of places and transitions. Two of them are
very natural and can be found in the literature. The
other two operations are a little similar to those in
(Berthelot, 1987). Suppose the original nets are
regular. We will prove that, for two of the four
compositional operations, the regularity can be
automatically preserved. For the other two ones,
some simple conditions will be provided under
which the regularity can be preserved.
3.1 Merging a Pair Of Places From
Two Nets
COMPOSITION-BY-PLACE (composition via
merging a pair of places from two different nets):
Consider two disconnected ordinary nets N
1
= (P
1
∪
ICINCO 2005 - ROBOTICS AND AUTOMATION
170

{p
1
}, T
1
, F
1
) and N
2
= (P
2
∪ {p
2
}, T
2
, F
2
), where T
1
∩ T
2
= ∅ and F
1
∩ F
2
= ∅. Let N be composed from
N
1
and N
2
by merging the pair of places p
1
and p
2
into p
12
, that is, N = (P, T, F), where P = P
1
∪ P
2
∪
{p
12
}, T = T
1
∪ T
2
and F = F
1
∪ F
2
.
Theorem 1: Let N, N
1
and N
2
be defined in
COMPOSITION-BY-PLACE. Then, N is regular if
N
1
and N
2
are regular.
Proof: In order to show that N is regular, we
must prove that N is connected, has a positive P-
invariant and a positive T-invariant, and satisfies:
Rank(N) = |C
N
| – 1. The incidence matrices of N, N
1
and N
2
have the forms:
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
32
22
31
11
21
12
2
1
0
0
V
V
V
V
TT
p
P
P
V
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
31
11
1
1
11
V
V
T
p
PV
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
32
22
2
2
22
V
V
T
p
PV
(1) Since N
1
and N
2
are connected, it is obvious that
N is also connected.
(2) Since N
1
and N
2
have positive P-invariants,
there exist
α
1
and
α
2
such that
α
1
> 0,
α
2
> 0,
α
1
V
1
=
0 and
α
2
V
2
= 0. Let
α
= (
α
2
(p
2
)
α
1|P1
α
1
(p
1
)
α
2|P2
α
1
(p
1
)
α
2
(p
2
)). Then
α
> 0 and
α
V = (
α
2
(p
2
)
α
1|P1
V
11
+
α
1
(p
1
)
α
2
(p
2
)V
31
α
1
(p
1
)
α
2|P2
V
22
+
α
1
(p
1
)
α
2
(p
2
)V
32
)
=(
α
2
(p
2
)(
α
1|P1
V
11
+
α
1
(p
1
)V
31
)
α
1
(p
1
)(
α
2|P2
V
22
+
α
2
(p
2
)V
32
)) =(
α
2
(p
2
)
α
1
V
1
α
1
(p
1
)
α
2
V
2
)
= 0. This means that
α
is a positive P-invariant of N.
(3) Since N
1
and N
2
have positive T-invariants,
there exist
β
1
and
β
2
such that
β
1
> 0,
β
2
> 0,
V
1
T
1
β
= 0 and V
2
T
2
β
= 0. This means that V
11
T
1
β
=
0, V
31
T
1
β
= 0, V
22
T
2
β
= 0 and V
32
T
2
β
= 0.
Let
β
= (
β
1
β
2
), then V
T
β
=
T
TTTT
VVVV )(
232131222111
ββββ
+
= 0. That
is,
β
is a T-invariant of N.
(4) Since Rank(V
1
) = |C(N
1
)| − 1 and Rank(V
2
) =
|C(N
2
)| − 1 and |C(N
1
)| ≤ |P
1
| and |C(N
2
)| ≤ |P
2
|,
Rank(V
1
) < |P
1
| and Rank(V
2
) < |P
2
|. Hence, the
bottom row V
3i
is a linear combination of the other
rows of V
ii
and Rank(V
i
) = Rank(V
ii
) for i = 1 and 2.
This also implies that the bottom row of V is a linear
combination of the other rows of V and Rank(V) =
Rank(V
11
) + Rank(V
22
) = (|C(N
1
)| − 1) + (|C(N
2
)| − 1).
Since the only change in clustering after
COMPOSITION-BY-PLACE is that the two clusters
([p
1
] in N
1
) and ([p
2
] in N
2
) are merged to one, we
have |C(N)| = |C(N
1
)| + |C(N
2
)| −1. Thus, Rank(V) =
(|C(N
1
)| − 1) + (|C(N
2
)| − 1) = |C(N)| − 1. □
3.2 Merging Two Non-neighboring
Places In A Net
MERGE-N-PLACE (merging two non-neighboring
places in a net): Let a net N = (P
0
∪ {p
1
, p
2
}, T, F)
be a net and p
1
and p
2
satisfy: (
•
p
1
∪ p
1
•
) ∩ (
•
p
2
∪
p
2
•
) = ∅. Let N' = (P
0
∪ {p
12
}, T, F') be obtained
from N by merging the places p
1
and p
2
into a single
place p
12
, where F' = F ∪ {(t, p
12
) | (t, p
1
) ∈ F or (t,
p
2
) ∈ F} ∪ {(p
12
, t) | (p
1
, t) ∈ F or (p
2
, t) ∈ F} − {(t,
p
i
) | (t, p
i
) ∈ F, where i = 1, 2} − {(p
i
, t) | (p
i
, t) ∈ F,
where i = 1, 2}.
Note that since this paper just considers pure
and ordinary nets, we add some conditions to p
1
and
p
2
, i.e., just considering non-neighboring places to
be merged.
Theorem 2 below proposes a simple condition
under which the regularity can be preserved after
applying MERGE-N-PLACE.
Theorem 2: Let N and N' be involved in
MERGE-N-PLACE, where N = (P
0
∪ {p
1
, p
2
}, T, F)
and N' = (P
0
∪ {p
12
}, T', F'). Then, N' is regular if
the following conditions hold:
(1) N is regular.
(2) there exists a positive P-invariant of N α such
that α(p
1
) = α(p
2
).
(3) p
1
and p
2
belong to the same cluster, and
(4) there exists at least one P-invariant α such that
〉
〈
α
∩ {p
1
, p
2
} = {p
i
}, where i = 1 or 2.
Proof: The incidence matrices of N and N' have
the following forms:
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
2
1
0
2
1
0
V
V
V
p
p
P
V
T
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
21
0
12
0
'
VV
V
p
P
T
V
(1) Since N is regular, N is connected. It is obvious
that N' is also connected.
(2) Since there exists a positive P-invariant of N α
such that α(p
1
) = α(p
2
), let
'
α
= (α
|P0
α(p
1
)) and
''V
α
= α
|P0
V
0
+
α
(p
1
)(V
1
+ V
2
) = α
|P0
V
0
+
α
(p
1
)V
1
+
α
(p
2
)V
2
= 0. This means that
α
is a positive P-
invariant of N'.
(3) Since N is regular, N has a positive T-invariant.
Let
β
be a positive T-invariant of N, then V
T
β
= 0.
It is obvious that
'V
T
β
= 0. That is,
β
also is a T-
invariant of N'.
(4) Since p
1
and p
2
belong to the same cluster,
|C(N')| = |C(N)|. Suppose that there exists one P-
invariant
α
such that
〉
〈
α
∩ {p
1
, p
2
} = {p
2
}. Then,
the corresponding row of p
2
in V can be expressed as
COMPOSITIONAL ANALYSIS FOR REGULARITY, LIVENESS AND BOUNDEDNESS
171

a linear combination of the other rows of P
0
. Hence,
Rank(V') = Rank(V). This means that Rank(V') =
Rank(V) = |C(N)| − 1 = |C(N')| − 1. □
It is obvious from the proof of Theorem 2 that
when p
1
and p
2
belong to different cluster, N' must
be not regular if N is regular and Condition (3) holds.
3.3 Merging A Pair Of Transitions
From Two Nets
COMPOSITION-BY-TRANSITION (composition
via merging a pair of transitions from two different
nets): Consider two disconnected ordinary nets N
1
=
(P
1
, T
1
∪ {t
1
}, F
1
) and N
2
= (P
2
, T
2
∪ {t
2
}, F
2
),
where P
1
∩ P
2
= ∅, (T
1
∪ {t
1
}) ∩ (T
2
∪ {t
2
}) = ∅,
T
1
∩ {t
1
} = ∅, T
2
∩ {t
2
} = ∅ and F
1
∩ F
2
= ∅. Let
N be composed from N
1
and N
2
by merging the pair
of transitions t
1
and t
2
. That is, N = (P, T, F), where
P = P
1
∪ P
2
, T = T
1
∪ T
2
∪ {t
12
} and F = F
1
∪ F
2
.
Theorem 3: Let N, N
1
and N
2
be defined in
COMPOSITION-BY-TRANSITION. Then, N is
regular if N
1
and N
2
are regular.
Proof: Similar to that of Theorem 1.□
3.4 Merging Two Non-neighboring
Transitions In A Net
MERGE-N-TRANSITION (merging two
transitions in a net): Let a net N = (P, T
0
∪ {t
1
, t
2
},
F) be a net and satisfy the following conditions: (
•
t
1
∪ t
1
•
) ∩ (
•
t
2
∪ t
2
•
) = ∅. Let N' = (P, T
0
∪ {t
12
}, F')
be obtained from N by merging the transitions t
1
and
t
2
into a single place t
12
, where F' = F' = F ∪ {(t
12
, p)
| (t
1
, p) ∈ F or (t
2
, p) ∈ F} ∪ {(p, t
12
) | (p, t
1
) ∈ F or
(p, t
2
) ∈ F} − {(t
i
, p) | (t
i
, p) ∈ F, where i = 1, 2} −
{(p, t
i
) | (p, t
i
) ∈ F, where i = 1, 2}.
Note that since this paper just considers pure
and ordinary nets, we add some conditions to t
1
and
t
2
, i.e., just considering non-neighboring transitions
to be merged.
Theorem 4: Let N and N' be involved in
MERGE-N-TRANSITION, where N = (P, T
0
∪ {t
1
,
t
2
}, F) and N' = (P, T
0
∪ {t
12
}, F'). Then, N' is
regular if the following conditions hold:
(1) N is regular,
(2) there exists a positive T-invariant
β
such that
β
(t
1
) =
β
(t
2
),
(3) t
1
and t
2
belong to the same cluster, and
(4) there exists at least one T-invariant
β
such that
〉〈
β
∩ {t
1
, t
2
} = {t
i
}, where i = 1 or 2.
Proof: Similar to that of Theorem 2. □
4 PRESERVING LIVENESS AND
BOUNDEDNESS
Desel and Esparza have shown that the regularity
guarantees the existence of a live and bounded
marking. This section will decide if a given initial
marking M
0
ensures liveness and boundedness of (N,
M
0
), where N is the net obtained by applying the
four compositional operations defined in Section 3.
Lemma 1 below characterizes liveness and
boundedness of regular nets.
Lemma 1: (Desel and Esparza, 1995) Let N be
a regular net. Then, a marking M of N is live and
bounded iff it marks all minimal siphons of N.
In order to check whether the liveness and
boundedness of a marked regular net, it is important
to know whether all siphons are marked after
applying the four compositional operations. The
following propositions state the relationship of
siphons of nets of before and after transformation.
Proposition 1: Suppose that N, N
1
and N
2
are
defined in COMPOSITION-BY-PLACE. Let D be a
siphon of N. Then, D
i
= D ∩ P
i
is a siphon of N
i
if
p
12
∉
D, otherwise D
i
= (D ∩ P
i
) ∪ {p
i
} is a siphon
of N
i
, where i = 1 and 2.
Proof: Since D is a siphon of N,
•
D ⊆ D
•
. Since
P
1
∩ P
2
= ∅, T
1
∩ T
2
= ∅ and D = (D ∩ P
1
) ∪ (D ∩
P
2
) =D
1
∪ D
2
if p
12
∉
D, it is obvious that
•
D
1
⊆ D
1
•
and
•
D
2
⊆ D
2
•
. This means that D
i
= D ∩ P
i
is a
siphon of N
i
if p
12
∉
D. If p
12
∈ D, then
•
p
12
in N =
(
•
p
1
in N
1
) ∪ (
•
p
2
in N
2
) and p
12
•
in N = (p
1
•
in N
1
) ∪
(p
2
•
in N
2
). Since
•
D ⊆ D
•
and T
1
∩ T
2
= ∅,
•
((D ∩
P
i
) ∪ {p
i
}) ⊆ ((D ∩ P
i
) ∪ {p
i
})
•
, this means that (D
∩ P
i
) ∪ {p
i
}
is a siphon of N
i
, where i =1 and 2. □
Proposition 2: Suppose that N and N' are
defined in MERGE-N-PLACE. Let D' be a siphon of
N'. Then, D' is a siphon of N if p
12
∉D', otherwise D
= D' ∪ {p
1
, p
2
} − {p
12
} is a siphon of N.
Proof: Since D' is a siphon of N',
•
D' ⊆ D'
•
in
N'. It is obvious that
•
D' ⊆ D'
•
in N if p
12
∉D'. This
means that D' is a siphon of N. If p
12
∈ D', then
•
p
12
in N' = (
•
p
1
∪
•
p
2
) in N and p
12
•
in N' = (p
1
•
∪ p
2
•
) in
N. Since
•
D' ⊆ D'
•
,
•
(D' ∪ {p
1
, p
2
} − {p
12
}) ⊆ (D' ∪
{p
1
, p
2
} − {p
12
})
•
, this means that D' ∪ {p
1
, p
2
} −
{p
12
}
is a siphon of N. □
Proposition 3: Suppose that N, N
1
and N
2
are
defined in COMPOSITION-BY-TRANSITION. Let
D be a siphon of N. Then, D
i
= D ∩ P
i
is a siphon of
N
i
, where i = 1 or 2.
Proof: Since P
1
∩ P
2
= ∅, T
1
∩ T
2
= ∅ and D
= (D ∩ P
1
) ∪ (D ∩ P
2
) =D
1
∪ D
2
, it is obvious that
•
D
1
⊆ D
1
•
and
•
D
2
⊆ D
2
•
because of
•
D ⊆ D
•
. □
ICINCO 2005 - ROBOTICS AND AUTOMATION
172
Proposition 4: Suppose that N and N' are
defined in MERGE-N-TRANSITION. Let D' be a
siphon of N'. Then, D' is a siphon of N if {t
12
}
∉
•
D'.
Proof: Since D' is a siphon of N',
•
D' ⊆ D'
•
in
N'. It is obvious that
•
D' ⊆ D'
•
in N if {t
12
}
∉
•
D', i.e.,
D' is a siphon of N if {t
12
}
∉
•
D'. □
Theorem 5: Suppose that N
and N
i
are defined
in COMPOSITION-BY-PLACE. Let M
i
be an initial
marking of N
i
and M be obtained from M
i
such that
M(p) = M
i
(p) if p ∈ P
i
− {p
1
, p
2
} and M(p
12
) =
Max{M
1
(p
1
), M
2
(p
2
)}. Then, (N, M) is live and
bounded if N
i
is regular and (N
i
, M
i
) is live and
bounded, where i = 1 and 2.
Proof: Since N
1
and N
2
are regular, by Theorem
3.1, N is regular. Since (N
1
, M
1
) and (N
2
, M
2
) are live
and bounded, according to Lemma 1, all siphons of
N
1
and N
2
are marked. Let D be a siphon of N. By
Proposition 1, if p
12
∉ D, then D
i
= D ∩ P
i
is a
siphon of N
i
. Hence, D
i
is marked. If p
12
∈ D, then
(D ∩ P
i
) ∪ {p
i
}
is a siphon of N
i
by Property 1 and
thus (D ∩ P
i
) ∪ {p
i
} is marked. In this case, if p
i
is
marked for i = 1 or 2, then p
12
is marked, otherwise,
D ∩ P
i
is marked. This means that all siphons of N
are marked. Thus, (M, N) is live and bounded
according to Lemma 1. □
Theorem 6 Suppose that N and N' are defined
in MERGE-N-PLACE, and M is an initial marking
of N. Let M' be obtained from M such that M'(p) =
M(p) if p ∈ P − {p
1
, p
2
} and M'(p
12
) = Max{M(p
1
),
M(p
2
)}. Then, (N', M') is live and bounded if the
following conditions hold:
(1) N is regular,
(2) p
1
and p
2
belong to the same cluster,
(3) there exists a positive P-invariant of N α such
that α(p
1
) = α(p
2
),
(4) there exists at least one P-invariant α such that
〉〈
α
∩ {p
1
, p
2
} = {p
i
} for i = 1 or 2, and
(5) (N, M) is live and bounded.
Proof: By Conditions (1)-(4) and Theorem 2,
N' is regular. Condition (5) implies that all siphons
are marked according to Lemma 1. Consider any
siphon D' of N'. By Proposition 2, if p
12
∉D', then D
= D' is a siphon of N. Hence, D is marked. If p
12
∈
D', then (D ∩ P) ∪ {p
1
, p
2
}
is a siphon of N and thus
is marked. This means that all siphons of N' are
marked. Thus, (N, M) is live and bounded according
to Lemma 1. □
The example below shows the application of
some results obtained in Section 3 and this section.
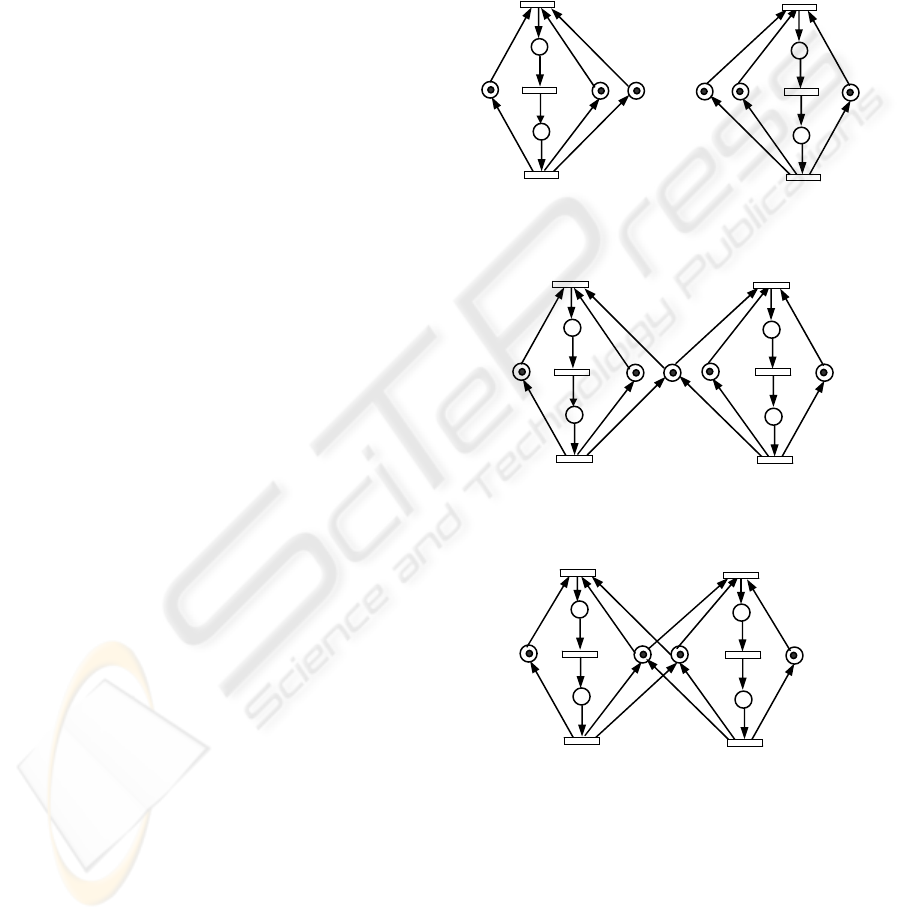
Example 1: In Figure 1, both (N
1
, M
1
) and (N
2
,
M
2
) are live and bounded marked graphs. Of course,
N
1
and N
2
are regular. After applying
COMPOSITION-BY-PLACE to them, p
1
and p
2
are
merged into r
1
and (N, M) shown in Figure 2 is
obtained. By Theorem 1 and Theorem 5, N is regular
and (N, M) is live and bounded. After applying
MERGE-N-PLACE to (N, M), p
3
and p
4
are merged
into r
2
and (N', M') shown in Figure 3 is obtained.
Since, in N, p
3
and p
4
belong to the same cluster and
{p
3
, p
12
, p
13
} is a P-component, by Theorem 2 and
Theorem 6, N' is also regular and (N', M') is live and
bounded.
Theorem 7: Suppose that N
and N
i
are defined
in COMPOSITION-BY-TRANSITION. Let M
i
be
an initial marking of N
i
and M be obtained from M
i
such that M(p) = M
i
(p) if p ∈ P
i
. Then, (N, M) is live
and bounded if N
i
is regular and (N
i
, M
i
) is live and
bounded, where i = 1 and 2.
Proof: Similar to the proof of Theorem 5. □
p
11
p
12
p
13
t
11
t
12
t
13
p
3
p
1
(N
1
, M
1
)
p
4
t
21
p
21
p
23
p
22
t
22
t
23
p
2
(N
2
, M
2
)
Figure 1: Two live and bounded Petri nets
p
11
p
12
p
13
t
11
t
12
t
13
r
1
p
3
p
4
t
21
p
21
p
23
p
22
t
22
t
23
Figure 2: Petri net (N, M) obtained from Figure 1
by merging p
1
and p
2
into r
1
.
p
11
p
12
p
14
t
11
t
12
t
13
r
2
r
1
t
21
p
21
p
25
p
23
t
22
t
23
Figure 3: Petri net (N', M') obtained from Figure 2
by merging p
3
and p
4
into r
2
.
COMPOSITIONAL ANALYSIS FOR REGULARITY, LIVENESS AND BOUNDEDNESS
173

Theorem 8: Suppose that N and N' are defined
in MERGE-N-TRANSITION. Let M be an initial
marking of N and M' be obtained from M such that
M'(p) = M(p) for any p ∈ P. Then, (N', M') is live
and bounded if the following conditions hold:
(1) N is regular,
(2) t
1
and t
2
belong to the same cluster,
(3) there exists a positive T-invariant
β
such that
β
(t
1
) =
β
(t
2
),
(4) there exists at least one T-invariant
β
such that
〉〈
β
∩ {t
1
, t
2
} = {t
i
} for i = 1 or 2, and
(5) (N, M) is live and bounded, and
(6) all input places of t
1
and t
2
are marked or every
minimal siphon D' of N' with t
12
∈
•
D' is marked.
Proof: By Conditions (1)-(4) and Theorem 4,
N' is regular. Condition (5) implies that all siphons
are marked according to Lemma 1. Consider any
siphon D' of N'. By Property 4, D' is a siphon of N if
{t
12
} ∉
•
D' and thus D' is marked. By Condition (6),
D' is marked if t
12
∈
•
D'. This means that all siphons
of N' are marked. Hence, (N, M) is live and bounded
according to Lemma 1. □
5 CONCLUSION
This paper studied four compositional operations in
terms of place and transition for pure and ordinary
nets and showed that regularity, liveness and
bounded-ness can be preserved automatically or
under some simper conditions. These compositional
operations are quite natural. COMPOSITION-BY-
PLACE and COMPOSITION-BY-TRANSITION
are usually be used to obtain more complex nets
from some subnets. Liveness and boundedness
preservations on the two operations for different
subclasses of Petri nets have been studied under
different conditions. Our results are based on the
regularity preservation. MERGE-N-PLACE and
MERGE-N-TRANSITION are two operations used
in a net, a little similar to (Berthelot, 1987). Of
course, these results that this paper are contributed
are new and can accommodate the design of
complex systems.
ACKNOWLEDGEMENTS
I would like to thank the anonymous referees for
their helpful comments. The research was funded by
the National Natural Science Foundation of China
under Grants No. 60473007 and No. 60421001.
REFERENCES
Berthelot, G., 1986. Checking properties of nets using
transformations. In: Rozenberg, G.: LNCS Vol. 222:
Advances in Petri nets 1985, pp. 19-40.
Berthelot, G., 1987. Transformations and decompositions
of nets. In: Brauer, W.; Reisig, W.; Rozenberg, G.,
editors: LNCS Vol. 254: Petri Nets: Central Models
and Their Properties, Advances in Petri Nets 1986,
Part I, Proceedings of an Advanced Course, Bad
Honnef, September 1986, pp. 359-376.
Desel, J., 1992. A proof of the rank theorem for extended
free choice nets. In Jensen, K., editor: LNCS Vol. 616,
Application and Theory of Petri Nets, Springer-
Verlag, pp. 134-183.
Desel, J. and Esparza, J., 1995. Free choice Petri nets.
London, Cambridge University Press.
Esparza, J. 1994. Reduction and synthesis of live and
bounded free choice Petri nets, Information and
Computation, Vol. 114, No. 1, pp. 50-87.
Huang, H., Jiao, L. and Cheung, T., 2005. Property-
preserving subnet reductions for designing
manufacturing systems with shared resources.
Theoretical Computer Science, 332(1-3), pp.461-485.
Koh, I. and DiCesare, F., 1991. Modular transformation
methods for generalized Petri nets and their
applications in manufacturing automation, IEEE
Transactions on Systems, Man and Cybernetics, 21, pp.
963-973.
Recalde, L., Teruel, E. and Silva, M., 1998. On linear
algebraic techniques for liveness analysis of P/T
systems, Journal of Circuits, Systems, and Computers,
8(1), pp.223-265.
Silva, M., Teruel, E. and Colom, J. M., 1998. Linear
algebraic and linear programming techniques for the
analysis of Place/Transition net systems, in Reisig, W.
and Rozenberg, G., editors: LNCS Vol. 1491, Lectures
on Petri Nets I: basic models, Springer-Verlag,
pp.309-373.
Souissi, Y., 1991. On liveness preservation by
composition of nets via a set of places, In: Rozenberg,
G., editor: LNCS Vol. 524, Advances in Petri Nets,
pp.277-295.
Suzuki, I. and Murata, T., 1983. A method for stepwise
refinement and abstraction of Petri nets, Journal of
Computer and System Sciences, 27, pp.51−76.
Valette, R., 1979. Analysis of Petri nets by stepwise
refinements, Journal of Computer and System
Sciences, 18, pp.35−46.
Zhou, M., 1996. Generalizing parallel and sequential
mutual exclusions for Petri net synthesis of
manufacturing systems, IEEE Int. Conf. On Emerging
Technologies and Factory Automation, 1, pp.49-55.
Zhou, M. and Venkatesh, K., 1999. Modeling, simulation,
and control of flexible manufacturing systems: A Petri
net approach, World Scientific Publishing Co. Pte.Ltd.
ICINCO 2005 - ROBOTICS AND AUTOMATION
174
