COMPARATIVE PERFORMANCE OF INTELLIGENT

IDENTIFICATION AND CONTROL ALGORITHMS FOR A

FLEXIBLE BEAM VIBRATION

M. A. Hossain, A. A. Madkour and K. P. Dahal

Modelling Optimization Scheduling And Intelligent Control (MOSAIC) Research Centre

Department of Computing, University of Bradford, Bradford, BD7 1DP, UK

Keywords: Performance issues, system identification, active vibration control, genetic algorithm, recursive least square

and ANFIS.

Abstract: This research presents an investigation into the comparative performance in implementing intelligent system

identification and control algorithms. Several approaches for on-line system identification and control are

explored and evaluated to demonstrate the merits in implementing the algorithms for similar level of error

convergence. Active vibration control (AVC) of a flexible beam system is considered as a platform for the

investigation. The AVC system is designed using three different on-line identification approaches, which

include (a) genetic algorithms (GAs) (b) adaptive neuro-fuzzy inference system (ANFIS) and (c) recursive

least square (RLS) estimation. These algorithms are used to estimate a linear discrete model of the system.

Based on these algorithms, different approaches of the AVC system are implemented, tested and validated

to evaluate the relative merits of the algorithms. Finally, a comparative performance of the error

convergence performance in implementing the identification and control algorithms is presented and

discussed through a set of experiments.

1 INTRODUCTION

Many demanding complex identification and control

algorithms cannot be satisfactorily realised in real-

time due to such computational complexity.

Comparative performance analysis of alternative

strategies, where multiple solutions are available,

could provide an opportunity to identify the best

algorithm(s). Many attempts have been made in the

past at devising methods of tackling the control

problem using artificial intelligence (Amato et al.,

2001; Hossain and Tokhi, 1997; Yamlidou et al.,

1996). Many attempts have also been made for real-

time control system implementation (Baxter et al.,

1994; Jones, 1989; Tokhi et al., 2002). However,

limited contributions have been reported on real-

time performance issues in implementing intelligent

identification and control algorithms (Albertos, et

al.,2001;Madkour et al, 2004).

The conventional on-line system identification

schemes, such as least squares, instrumental

variables and maximum likelihood are in essence

local search techniques. These techniques often fail

in the search for the global optimum if the search

space is not differentiable or linear in the

parameters. On the other hand, these techniques do

not iterate more than once on each datum received.

To address these issues, several approaches using

artificial intelligence (AI) techniques have been

reported earlier (Hossain and Tokhi, 1997). This

investigation considers some of these approaches to

explore comparative performance in implementing

the algorithms for same error convergence.

2 ALGORITHMS

The intelligent active vibration control algorithm

consists of flexible beam simulation algorithm,

control algorithm and system identification using

GAs, ANFIS and RLS algorithms. Therefore, three

approaches of AVC algorithm are designed based on

the three identification algorithms. These algorithms

are briefly described below.

364

A. Hossain M., A. Madkour A. and P. Dahal K. (2005).

COMPARATIVE PERFORMANCE OF INTELLIGENT IDENTIFICATION AND CONTROL ALGORITHMS FOR A FLEXIBLE BEAM VIBRATION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 364-367

DOI: 10.5220/0001179903640367

 SciTePress

2.1 Simulation and control

algorithms

Consider a cantilever beam system with a force

()

txF , applied at a distance

from its fixed

(clamped) end at time

. This will result in a

deflection

()

txy , of the beam from its stationary

position at the point where the force has been

applied. In this manner, the governing dynamic

equation of the beam is given by

() ()

()

txF

txy

∂

(1)

where,

is a beam constant and m is the mass of

the beam. Discretising the beam into a finite number

of sections (segments) of length

x∆ and considering

the deflection of each section at time steps

∆

using

the central FD method, a discrete approximation to

equation (1) can be obtained as (Kourmoulis, 1990)

(

)

()

txF

SYYY

kkk

∆

+−−=

−+

(2)

where,

()()

xt ∆∆=

µλ

, S is a pentadiagonal

matrix, entries of which depend on the physical

properties and boundary conditions of the beam, and

Y ( 1,,1 −+= kkki ) is a vector representing the

deflection of end of sections

to n of the beam at

time step

i . Equation (2) is the required relation for

the simulation algorithm.

Observed

Signal

Detector

Secondary

source

Primary

source

Figure 1: Active vibration control structure

A schematic diagram of an AVC structure is shown

in Figure 1. A single-input single-output (SISO)

AVC system is considered for vibration suppression

of the beam. The unwanted (primary) disturbance is

detected by a detection sensor, processed by a

controller to generate a cancelling (secondary,

control) signal so as to achieve cancellation at an

observation point along the beam.

The objective in Figure 1 is to achieve total

(optimum) vibration suppression at the observation

point. This requires the primary and secondary

signals at the observation point to be equal in

amplitudes and to have a

180 phase difference.

ANFIS, GAs and RLS algorithms are used as

system identification algorithms to estimate the

AVC system cancelling signal. To identify the

cancelling signal, a linear discrete second order

model will be estimated using ANFIS, GA and RLS.

)(

)()(1

)(

zaza

zbzb

−−

(3)

where Y is the system input and U is its output

2.2 Identification algorithms

2.2.1 Adaptive neuro-fuzzy inference system

The hybrid Adaptive Neuro-Fuzzy inference

system(ANFIS) provides a method of fuzzy

modelling to learn information about a data set, in

order to compute the membership function

parameters that best allow the associated fuzzy

inference system to track the given input-output

data. ANFIS has been proven to be an excellent

function approximation tool (Jian, 1993). This

function is used for system identification, which is a

major training routine of Sugeno-type FIS (fuzzy

inference system).

2.2.2 Genetic algorithms

A Genetic Algorithm (GA) simultaneously evaluates

many points in the parameter space and converges

more likely towards the global solution. This

algorithm differs from other search techniques in

that it uses concepts taken from natural genetics and

evolution theory. The GA is used based on the

method of minimization of the prediction error. The

method of evolutionary computation works as

follows: create a population of individuals, evaluate

their fitness, generate a new population by applying

genetic operators, and repeat this process for a

number of times Genetic algorithms consider the

same multi parameter system given by equation (3)

with the following fitness function (Hossain and

Tokhi, 1997):

∑

−=

kykyrJ

)(

)()( (4)

where,

)(ky is measured output, )(

ky is estimated

model output, and

is the number of sets of

measurement considered.

COMPARATIVE PERFORMANCE OF INTELLIGENT IDENTIFICATION AND CONTROL ALGORITHMS FOR A

FLEXIBLE BEAM VIBRATION

365

2.2.3 RLS algorithm

This is a well-known traditional adaptive filter

algorithm estimates the current parameter vector

)(

based on the previous estimated vector

)1(

−k

Estimation of the parameter vector

is performed

such that the estimate

minimizes the cost

index

)(rJ , where

denotes the number of sets of

measurement (Madkour et al., 2004)

3 IMPLEMENTATION AND

RESULTS

A cantilever beam in transverse vibration of length

m 635.0=L , mass kg 037.0=m , was considered.

The beam was discretised into 19 equal-length

segments. To allow dominant modes of vibration of

the beam to be excited, a finite-duration step

disturbance force of amplitude

N 1.0 was applied to

the beam. The input and output samples of the plant

were collected from two separate points on the

beam. The sample period was selected as

ms 3.0=∆t , which is sufficient to cover all the

dominant resonance modes of vibration of the beam

(Hossain, 1995).

To identify the cancelling signal, a linear discrete

second order model was estimated using ANFIS,

GA and RLS.

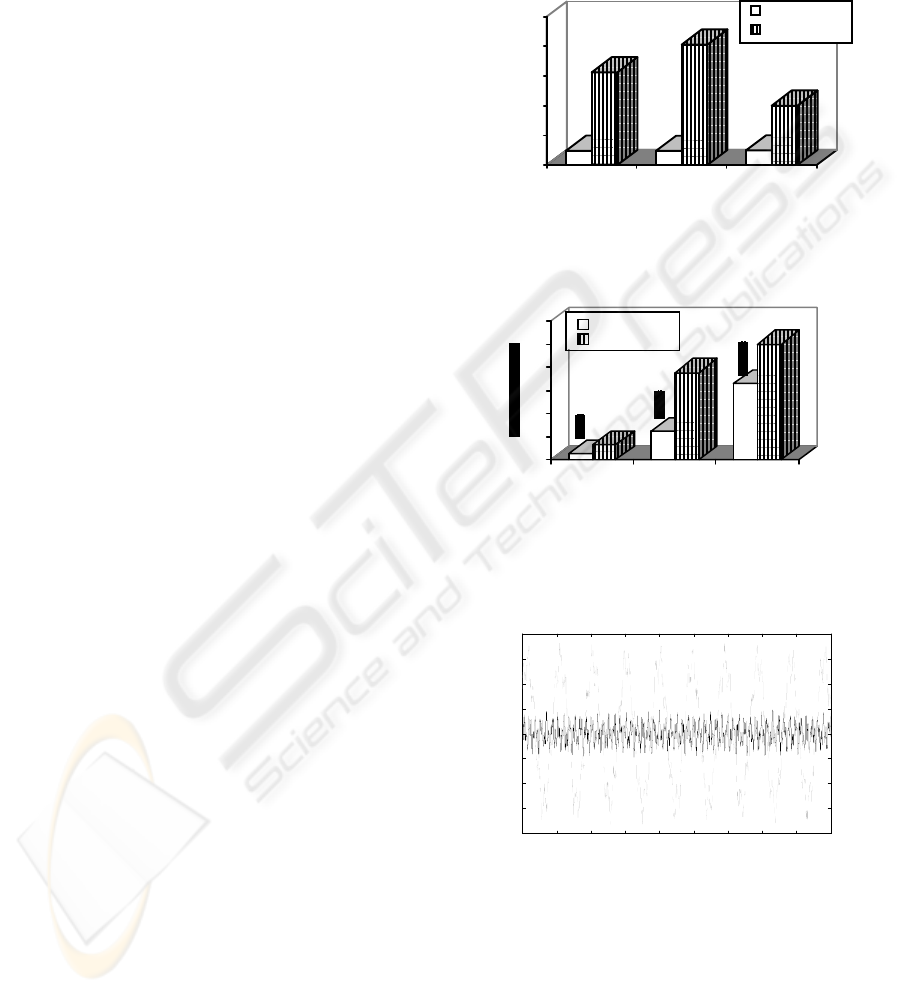
Figure 2 shows the error convergence and the

real-time performances of the algorithms. It is worth

mentioning that the error has been calculated based

on the differences between absolute value of the

original and the estimated signal. On the other hand,

the execution time of the algorithms was measured

for 6000 iterations with

ms 3.0 sampling time.

Therefore, the maximum execution time of the

algorithms in implementing real-time should be

s 8.1 . It is worth noting that for the sake of better

investigation on execution time, error convergences

for all the algorithms were considered to be within a

similar level. However, an insignificant error

convergence variation is observed during

implementation. With regard to the execution time

in implementing the system identification

algorithms, all the algorithms achieved real-time

performance. It is noted that the RLS algorithm

offers the best performance and ANFIS offers the

worst performance among the three algorithms. It is

also noted that the execution time in implementing

ANFIS is double as compared to the RLS algorithm

and 1.56 times as compared to the GA.

It is also observed that performance of the GA

based system identification varies due to the bit

representation and population size. Therefore, a

further investigation was made to explore and

demonstrate this issue. Figure 3 shows execution

times in implementing the GA based system

identification algorithms for 8 and 16 bits

representation. It is observed that except population

with 10 of 8 bit representation, none of the other

situations achieved real-time performance.

0.2412

1.56

0.2383

2.03

0.2465

0.5

1.5

2.5

Execution time (s)

GAs ANFIS RLS

Algorithms for system identification

Error Conver.

Relative Time

Figure 2: Relative performance in implementing the

system identification algorithms

3.121

18 .8 9

25.051

10 5 0 10 0

Populat ion Size

8 bits rep.

16 bits rep.

Figure 3: Performance of GA for 8 and 16 bits

representation

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

-8

-6

-4

-2

x 10

-4

Tim e (sec )

Deflection (m)

Figure 4: Performance in implementing the AVC

algorithm using ANFIS

Figures 4, 5 and 6 show the time-domain

performance in implementing the AVC system

using, ANFIS, GA and RLS algorithms, where the

dotted and solid lines represent fluctuation of the

beam at the end point before and after cancellation.

It is noted that ANFIS offers the best and RLS the

worst performance among the three methods. It is

also noted that the peak to peak end-point

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

366

fluctuation after cancellation using ANFIS is 4, GA

is 1.8 and RLS is 1.2 times smaller as compared to

the fluctuation before cancellation.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

-8

-6

-4

-2

x 10

-4

Tim e (s e c )

Defl ection (m)

Figure 5: Performance in implementing the AVC

algorithm using GA

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

-8

-6

-4

-2

x 10

-4

Tim e (s e c )

Defl ecti on (m)

Figure 6: Performance in implementing the AVC

algorithm using RLS

4 CONCLUDING REMARKS

This paper has presented the relative real-time

performance and error convergence issues in

implementing system identification and AVC system

of a flexible beam vibration using, ANFIS, GA and

RLS algorithm. A comparative performance of the

algorithms has been presented and discussed through

a set of experiments. For system identification, it is

noted that the execution time in implementing

ANFIS as compared to GA and RLS is significantly

higher. However, ANFIS shows slightly better error

convergence for the same number of iterations. On

the other hand, real-time computing performance of

GA varies based on the selection of the size of

population and binary representation. It is noted that

the GA with higher bit representation and larger

population size for the same error convergence

performs slower than ANFIS. It is also noted that the

execution time for each of the three algorithms is

less than the sampling time, in turn satisfying the

real-time requirement. However, in case of GA, this

is true only for population size 10 with 8 bit

representation.

REFERENCES

Albertos, P., Crespo, A. and Simo, J. (2001). Real-time

constraints in intelligent control,

http://www.delet.ufrgs.br/vsbai/vsbai/artigos/1156.pdf

Amato P., Farina, M., Palma, G. and Porto, D. (2001). An

alife-Inspired evolutionary algorithm for adaptive

control of time-varying system, Proc EUROGEN

2001, Athens, Greece, pp. 15-16

Baxter, M. J., Tokhi, M. O. and Fleming, P. J. (1994).

Parallelising algorithms to exploit heterogeneous

architectures for real-time control systems,

Proceedings of IEE Control-94 Conference, Coventry,

21-24 March 1994, 2, pp. 1266-1271.

Hossain, M. A. (1995). Digital signal processing and

parallel processing for real-time adaptive noise and

vibration control, Ph.D. thesis, Department of

Automatic Control and System Engineering, The

University of Sheffield, UK.

Hossain, M. A. and Tokhi, M. O. (1997). Evolutionary

adaptive active vibration control, Proc Inst.

Mechanical Eng., 211(1), pp. 183-193.

Jang, J. S. R. (1993). ANFIS: Adaptive-Network-based

Fuzzy Inference Systems, IEEE Transactions on

Systems, Man, and Cybernetics, 23(3), pp. 665-685,

1993.

Jones, D. I. (1989). Parallel architectures for real-time

control, Electronics and Communications Engineering

Journal, 1(5), 217-224.

Kourmoulis, P. K. (1990). "Parallel processing in the

simulation and control of flexible beam structure

systems", PhD thesis, Dept. of Automatic Control &

Systems Engineering, The University of Sheffield.

Madkour, A. A. M., Hossain, M. A., Dahal, K. P. and Yu,

H., (2004). Real-time System Identification using

Intelligent Algorithms, Proceedings of IEEE SMC

UK-RI Chapter Conference 2004 on Intelligent

Cybernetic Systems, pp. 236-241.

Tokhi, M. O. and Hossain, M. A. (1994). Self-tuning

active vibration control in flexible beam structures,

Proc. IMECE-I: J. Systems Control Eng. 208(14), pp.

263-277.

Tokhi, M. O., Hossain, M. A. and Shaheed, M. H. (2002).

Parallel Computing for Real-time Signal Processing

and Control, Springer, London.

Yamlidou, K. Moody, J., Lemmon, M. and Antsaklis, P.

(1996). Feedback control of Petri nets based on place

invariants, Automatica, 32(1), pp. 15-28.

COMPARATIVE PERFORMANCE OF INTELLIGENT IDENTIFICATION AND CONTROL ALGORITHMS FOR A

FLEXIBLE BEAM VIBRATION

367