
ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH
BASED ON LOCAL COMMUNICATION AND SENSING
Damien Bright
KnowledgeLab, University of Southern Denmark
Campusvej 55, DK-5230 Odense M, Denmark
Keywords:
simulation, collective robotics, stigmergy, reinforced random walk, optimization.
Abstract:
This paper presents a simulation model for experimenting with locally adaptive movement strategies for robots
involved in collective robotic search tasks in rapidly changing and uncertain environments. The model assumes
that the nature of the environment restricts inter-robot communication and uses a form of stigmergy based
local communication which has been widely applied in collective robots. The model is based on a biased
random walk where the degree of bias is linked to a local control variable which can change depending on
the evaluation of local adaption strategies. The local adaption strategies use an approach based on activation
functions to control the choice of which candidate paths should be inhibited or have increased preference over
random motion. Experiments aim to test the effectiveness of this approach for optimal collective search in
various test domains. A series of initial experiments is presented demontrating aspects of the model.
1 INTRODUCTION
Studies of foraging behaviour in insects and animals
have been used by many researchers in collective ro-
botics as a model for experimenting with search be-
haviour for robots (eg (Balch and Arkin, 1994)). The
modeling of foraging can be divided at a general level
into macroscopic or microscopic approaches where
the former is used to model the actions of large num-
bers of entities and the latter the actions of individ-
uals. It has been found that there are advantages in
the use of microscopic models with a high degree
of localization and the use of external communica-
tion mechanisms in improving the ability of collabo-
rating robots ((Holland and Melhuish, 1999), (Wag-
ner et al., 1999),(Montgomery and Randall, 2002))
to perform foraging or search type tasks. This is of-
ten because robots generally have independent control
software and it is advantageous to remove the need
to maintain direct communication and shared knowl-
edge of individuals exact locations between multiple
robots which can be difficult to support in uncertain
and highly dynamic (i.e. rapidly changing) environ-
ments.
External communication mechanisms have at-
tracted considerable interest from collective robotics
and AI life researchers. In particular, the concept of
stigmergy (Holland and Melhuish, 1999) which de-
scribes a form of indirect communication utilizing the
environment as the communication medium has been
widely studied. Stigmergeric cues or markers rep-
resent a change made to the environment that com-
municates information and can take many forms E.g.
this could involve the use of beacons to guide robots
for tasks such as robot search and rescue. A much
studied form of stigmergeric marker is the use of
pheromone for trail marking where a chemical marker
(pheromone) is deposited. Entities in the system have
a pre-disposition to follow the strongest pheromone
trails they encounter and pheromone trails evaporate
(decay) over time which is useful for optimization.
Usually pheromone is considered as an attractant but
(Montgomery and Randall, 2002) has introduced the
concept of anti-pheromone as a useful tool for explor-
ing a search space. This is related to the fact that
a useful pure reactive strategy for search is to avoid
previously covered terrain which can be marked with
negative bias in the form of anti-pheromone.
Recent research in areas such as adaptive control
and optimization methods has examined the idea of
locally adaptive strategy within some search space.
For example this approach has been used in Genetic
algorithm (GA) work e.g. see (Igel et al., 2005) and
”self-tuning” methods for robotic control (Patterson
335
Bright D. (2005).
ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH BASED ON LOCAL COMMUNICATION AND SENSING.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 335-340
DOI: 10.5220/0001186503350340
Copyright
c
SciTePress

and Kautz, 2001). A large body of past research in
general optimization techniques such as gradient de-
scent and simulated annealing (Glover and Kochen-
berger, 2003) has also shown that the inclusion of ran-
dom processes can be important to achieving global
maxima/minima over local maxima/minima. Ro-
botic control which is purely reactive (like gradi-
ent following) can lead to the same type of local
maxmima/minima issues. The addition of random-
ness or noise into robotic motion has been shown to
help to avoid this (Balch and Arkin, 1994) but the
strategy used to determine the amount of random mo-
tion is generally fixed (ie not locally adaptive) and
therefore not well suited to time-dependent problems
requiring adaption to changing or uncertain environ-
mental conditions.
The main contribution of this paper is the devel-
opment of a simulation model based on a novel ap-
proach for representing local self-tuning or adaption
strategies within the context of optimization of multi-
robot search in complex and dynamic domains. A key
aim of the simulation model is to be able to study
in detail the use and effect of local strategies which
vary the degree to which reactive behaviour to marker
trails and reinforcement of marker trails should dom-
inate over random motions. The random walk model
used in this paper can be compared to a markov de-
cision process and has influences from reinforcement
learning theory (Kaelbling et al., 1994). This paper is
structured as follows: First a brief summary is given
of related work, then the numerical model is defined
and a set of initial results is presented. A summary
and future work section then describes some of the
aims and proposed uses of the simulation model.
2 RELATED WORK
A large body of research in AI life applied to opti-
mization and guidance problems has made use of in-
direct communication techniques based on social in-
sects such as trail laying. This has led to the term
synthetic pheromone describing data structures in-
spired by chemical markers called pheromones from
biological systems. Research in collective robotics
(Holland and Melhuish, 1999) has made substantial
use of stigmergy and other concepts from AI life re-
search. Approaches based on such techniques can
a provide robust and adaptive indirect coordination
mechanism for collaborating entities such as robots
(Wagner et al., 1999). Multiple robots using such
techniques are particularly efficient for tasks such
as mapping unknown terrain which are well suited
to being performed collectively. Each robot needs
only relatively simple functionality to achieve com-
plex group behaviour. This reduces the complexity
and cost of each robot. Different approaches to navi-
gation strategy for indoor searching have been exam-
ined by (Gonzales-Banos and Latombe, 2002). One
approach to aid search behaviour has been the use of
coverage maps (Stachniss and Burgard, 2003) which
in a similar way to maker trails can be viewed as a
form of indirect communication stored in the environ-
ment. Lately there has been increased use of multi-
ple robots to perform specialized tasks (eg search and
rescue (Baltes and Anderson, 2003)). Some common
problems with multiple robot guidance are:
(1) Pure reactive navigation often suffers from local
minima issues due to limitations such as sensor range
and/or accuracy. It has been found that a combina-
tion of goal directed behaviour and reactive behaviour
can be an effective (Balch and Arkin, 1994) strategy
but this often requires more complex robot behaviour
such as the use of path planning algorithms.
(2) centralized versus de-centralized control and
whether to use localized and indirect communica-
tion. Decentralized control and indirect communi-
cation (see (Holland and Melhuish, 1999), (Wagner
et al., 1999)) can be very useful in complex and dy-
namic environments where the environment is spa-
tially/geographically complex or where the positions
of objects that exist in the environment change or the
environment itself is subject to uncertainty or change.
Also robots with limited ability to transmit and com-
municate over longer distances can benefit from an
approach based on local communication.
Random walk models have been widely used to
model movement patterns such as dispersion. It is
possible under certain conditions to look at local con-
trol decisions in a biased random walk as a form of
Markov decision process. (Azar et al., 1992) examine
optimal strategy applicable to time independent long
term behaviour of a random walk on a finite graph
where local movement decisions can be viewed in
terms of a controller selecting from a set of available
actions to bias the behaviour of a markov chain. This
type of approach has relevance for this paper but is not
able to address time dependent local strategy forma-
tion. A reinforced random walk model was first pro-
posed by Coppersmith and Diasconis (Coppersmith
and Diaconis, 1987) as way of modeling a person ex-
ploring a new city (See also (Davis, 1990)). Ran-
dom walk models can be used as an important part
of more specific models for spatial exploration and
cooperative interaction. For example a biased ran-
dom walk model which uses feedback with the en-
vironment to influence a walkers movement is the ac-
tive walker model originally formulated by (Lam and
Pochy, 1993).
ICINCO 2005 - ROBOTICS AND AUTOMATION
336
Figure 1: Single robot search on box canyon maze domain
with n
x
= 70, n
y
= 70, r
seed
= 2392093, R
d
= 0.0, and
ν = 0.95, nsteps = 5000, Starting position is (55, 35).
No strategy change is applied for this run.
3 NUMERICAL MODEL
The discrete time simulation model that is proposed
here is based on the mapping of values from a global
time dependent field m(x, y, t), which represents the
dynamic (changing) part of the environment. m is
used to store data for stigmergy style collective com-
munication and gives the value of a marker (ie a type
of synthetic pheromone) m at position (x, y) in a 2D
domain at time t. m is mapped to local vectors of
the form v
ij
, i = 0..N which represent the probabil-
ity of making one of N possible local choices (eg a
local control decision of picking an adjacent square
to move to) for robot j in the system on the next
timestep. Marker values m can be positive or neg-
ative representing an attractant marker or repulsant
marker respectively. The field m(x, y, t) influences
the movement of robots in the system but also changes
due to feedback affects from individual robots when
an robot changes its local environment by laying a
marker trail. Therefore the model represents a stig-
mergy based form of indirect communication between
robots using the environment as the communication
medium.
Locally visible values of m(x, y, t) can be viewed
as positive or negative weights applied to local robot
decisions. The default trail laying behaviour of a ro-
bot is to deposit an initial positive concentration (rep-
resented by a value) of a marker at the grid square
(with position (x, y)) it occupies at each timestep.
This initial value is represented in the model as a
value m with initial magnitude 1.0. The model also
supports a robot laying a negative pheromone trail in
which case the initial value of m would be −1.0. This
means that unreinforced marker will be represented as
a m value in the range [−1.0, 1.0]. The concentration
of a marker can be reinforced by a grid square being
visited multiple times with the result that the mag-
nitude of reinforced m can increase without bound
over time. The magnitude of the marker can also be
made to decay over time by specifying a decay rate
R
d
which is applied to all squares containing a value
of m at each timestep. Robots can also have vari-
able sensor range limitations. In this model the sen-
sor range along a straight line path is represented as a
scalar value R
sense
which is measured in terms of a
number of grid cells.
3.1 Domain specification
Domain boundaries and objects in the domain can be
represented in two ways in the model. There is a sta-
tic 2D function f(x, y) which can be used to define
locations (x, y) which block movement. These can
be used to represent objects in the domain where it
is assumed that the grid cells have a binary structure
(occupied or free). Global values from this function
are mapped to a local filter vector f
i
, i = 0..N which
has values of 0 or 1 and can be used to filter the avail-
able local choices. An robot cannot choose squares
that have been filtered out and this can be used to set
up rigid type boundary conditions.
Alternatively a type of reflective boundary condi-
tion can be set up by specifying sufficiently large neg-
ative and non-decaying values of m(x, y, t). In this
case the boundary value at a square acts as a repulsive
force on robots in the system in such a way that an ro-
bot will tend to move away in the opposite direction.
Combining these methods provide a flexible way to
specify complex domains and domain objects.
3.2 Local mappings
There are two important types of mapping that are
used in the model. First local vectors v
i
of the general
form:
v
i
, i = 0..N (1)
are used. Each v
i
represents a value related to the
probability of making choice i. The range of i rep-
resents the available number of local choices. In a
square type domain grid this can be used as part of
making a movement decision to one of 8 possible ad-
jacent squares (also known as a Moore neighborhood)
so in this case N = 7 in 1. All the results presented
in this paper use N = 7.
A superposition of vectors of type v
i
can be used
to combine a number of different effects that may in-
ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH BASED ON LOCAL COMMUNICATION
AND SENSING
337

fluence a movement decision (see main equations be-
low) of an robot. This is a flexible way to incorpo-
rate many factors that may influence decisions in the
model. Because many of the factors that can influ-
ence movement decisions are related to the state of
the environment it is necessary to extract global val-
ues from m(x, y, t) or f (x, y) for the (N + 1) local
squares visible by an individual robot in the system at
each timestep. This is the first type of mapping used
(global to local).
The other type of mapping relates to negative val-
ues of m(x, y, t). Because the value of v
i
repre-
sents a probability value it should be greater than
zero. Therefore there needs to be a way to map neg-
ative values of m(x, y, t) (which represent negative
weights) to a positive probability value. Since values
of m(x, y, t) are used to influence robot movement in
our model it has been chosen to map a negative value
of m(x, y, t) to a positive value of the same magni-
tude but in the opposite direction. This means a re-
pulsive effect on an robot movement decision is made
equivalent to an attractive effect in the opposite direc-
tion.
3.3 Main update equations
First we need to define a set of local vectors. A deci-
sion vector d
i
represents the final probabilities of an
robot moving in one of i possible directions; a weight
vector w
i
represents weight values assigned to each of
the i possible path choices which are locally visible to
an robot and which represents an estimate of the max-
imum gain associated with choosing to move along a
particular path; a random decision vector r
i
represents
pure random choice (ie equal values for all i direc-
tions); a reinforcement decision vector l
i
represents
locally visible values of the component of m(x, y, t)
due to reinforcement; and a filter vector f
i
represents
a mask on which of the i choices are allowed or not
allowed due to rigid boundary conditions.
The basis of the model is a biased random walk
equation applied to the movement of each robot in
the system at each time step ∆t. For each robot
A
k
, k = 1..M, where M is the total number of ro-
bots, this equation takes the form:
d
i
= [(1 − ν
i
)r
i
+ ν
i
m
i
]f
i
(2)
where i = 0..N and the parameter ν
i
controls the
degree to which pure random choice (represented by
r
i
) dominates over weighted or biased choice repre-
sented by m
i
. There is also a step size s associated
with the random walk. Equation 2 and the stepsize to-
gether define the biased random walk. The vector m
i
represents weights based on locally visible values of
m(x, y, t) in the neighborhood of the walker. Given
only a single walker and m
i
purely based on trail lay-
ing (of marker) by the single walker, then a high value
of ν
i
leads to a random walk that approximates a self
avoiding walk.
Using 2 it is possible to experiment with local adap-
tive control strategies for selecting values of ν
i
and s
for each walker at each time step. This paper focuses
on the choice of ν
i
and experiments with adaptive val-
ues of s are left to future work. The approach taken
in this paper is to link increases in the value of ν
i
to
direction choices that are weighted by reinforced val-
ues of the m(x, y, t) field. This creates a subset of
(greedy) candidate directions from the complete set of
possible direction choices. This subset may be empty
if no reinforced field values are locally visible. These
direction choices are candidates for increased bias in
their probability of selection against random choice.
The aim of a local adaptive strategy for ν
i
is to fur-
ther reduce this subset of possible candidates (if this
can be done) by inhibiting the choice of some candi-
dates. In this paper the strategy is evaluated by cal-
culating a set of measures along a path up to distance
R
sense
(maximum sensor range) in each candidate di-
rection. Initially 3 measures have been chosen: (1) the
magnitude of reinforcement; (2) the distance dist that
can be traversed before any boundaries or field objects
(such as another robot walker) are encountered; (3) a
path gradient estimate calculated along the path up to
dist. Using a simple perceptron type activation func-
tion a strategy is activated depending on the values
of the measures and a set of weights. Strategies that
are evaluated but not activated inhibit the choice of a
candidate direction.
More formally, we need to first calculate a rein-
forcement vector l
i
:
l
i
=
m
i
− 1.0 if m
i
> 1.0
0 if m
i
< 1.0
Then for each l
i
a vector r
ij
(j = 0..2) is calcu-
lated which contains the required measures. Given
the three chosen measures, we have r
i0
= l
i
, r
i1
as
the distance that can be traversed along the path be-
fore a boundary or object is encountered and r
i2
is
the path gradient estimate.
We define a strategy π for selecting a local con-
trol variable z as π
z
. The local strategy for selecting
ν(x, y, t) is then defined as:
π
ν
: ν = ν
0
+ p(r
i
, θ) ∗ f(l
i
, ν
0
, ν
max
) (4)
where f is an monotonically increasing scaling func-
tion of l
i
with lower limit ν
0
and upper limit ν
max
,
ν
0
equals a constant positive parameter σ in the range
[0, 1], ν
max
is 1.0, θ is a threshold value, and p is an
activation function defined as:
p(r
i
, θ) =
1.0 if
P
2
i=0
w
i
r
i
> θ,
−1.0 if
P
2
i=0
w
i
r
i
< θ.
ICINCO 2005 - ROBOTICS AND AUTOMATION
338

where the w
i
are weight parameters. Equation 4 is
equivalent to conditionally increasing ν, after cer-
tain conditions are satisfied which result in the ac-
tivation function firing, by a factor between ν
0
and
ν
max
which depends on the magnitude of l
i
. This is
based on a simple perceptron like behaviour to choose
an approximate new scaled value of ν in the range
[ν
0
, ν
max
].
The choice of a gradient measure in caculating r
i
is
used as a rough estimate of whether movement along
a particular path will lead towards less frequently tra-
versed parts of the domain (based on the m(x, y, t)
field). As part of calculating the gradient estimate, a
scalar discount factor ζ is introduced to discount val-
ues of m which are more than one cell away from
the walker and which may have uncertainty associ-
ated with them due to changes in a cell value that will
take place by the time the walker gets to that cell.
At each timestep ∆t the simulation moves each ro-
bot according to (Eq. 2) and updates m which is dis-
cretized on a i by j grid as follows:
m
i,j
(t + ∆t) = m
i,j
(t) + ξ
i,j
(t),
∀0 < i < nx, 0 < j < ny (6)
where ξ
i,j
(t) is based on the pheromone deposited
by robots during their movement (positive or nega-
tive) and the pheromone decay rate R
d
for the current
timestep. On each timestep the following heuristic is
applied:
1. Calculate m
i
from m(x, y, t)
2. Perform mappings (global to local, negative to pos-
itive)
3. ∀m
i
> 1.0, set l
i
= m
i
− 1.0 (else l
i
= 0) and
normalize m
i
, l
i
4. Calculate a set of r
i
(greedy candidate measures)
5. Apply local strategies π
ν
6. Calculate and normalize d
i
where normalization for a vector v
i
is calculated as
v
norm
i
=
v
i
i
v
i
. Due to normalization the strength-
ening of the probability of making one choice leads
automatically to the weakening of the probability of
choosing the other available choices.
3.3.1 Model parameters
The key model parameters are M the total number of
robots, n
x
, n
y
representing the discrete grid dimen-
sions, σ representing a constant ratio of random ef-
fects versus bias effects on robot movement, σ which
represents a threshold used to control the effect of re-
inforcement in the model, R
d
which represents the
decay rate applied to the magnitude of field values
m(x, y, t), nsteps represents the number of steps
taken in the simulation, and r
seed
representing the
seed value used for the random number generator.
w
i
(i = 0..1) are weight parameters which are in the
series of initial experiments described below are as-
signed values using the following rules: w
0
= 1.0/r
0
,
w
1
= r
1
/R
sense
; if ((|r
2
| > 1)AND(r
2
> 0)) then
w
2
= −1.0 else w
2
= 1.0.
4 RESULTS
A series of initial tests have been performed us-
ing a Java implementation of the model where
Java.util.Random was used as the random number
generator for randomly chosen motion. These tests
have all been performed with the following fixed
model parameters: nx = 70, ny = 70, r
seed
=
2392093, R
d
= 0.0, and with variable values for the
other parameters. The metric chosen here to evalu-
ate the model for domain coverage has been percent-
age coverage (of the bounded domain) versus time
(number of iterations). A standard sigmoid func-
tion has been used for the scaling function f with
exp(−(r
0
− σ))/2.
The first set of tests used just one robot to search
a maze type domain. Initially tests were undertaken
with no use of strategies and different values of σ (i.e.
this is the fixed value of ν = σ case). It was found that
as σ was increased in this case (with the random walk
becoming more like a self-avoiding walk) that the do-
main coverage also increased. At domain boundaries
a reflective boundary condition needs to be strongly
enforced and this is achieved using high negative
marker values and reinforcement (in direction choice)
to define the boundary. In Fig. 1 the use of local
strategies to adapt the value of ν was compared with
the fixed value (No strategy) case for σ = 0.75. The
results appear to indicate that the use of adaptive local
strategy can increase performance (domain coverage
versus time) but more experiments need to be per-
formed to examine this in detail. The strategy para-
meter sets used were Strategy1 = (θ = 2.8, σ = 0.75)
and Strategy2 = (θ = 2.5, σ = 0.75) with other para-
meters set as described above.
The next set of simulation tests demonstrated that
the model scales well as the number of robots is in-
creased. Figure (3) shows that as the number of ro-
bots is increased from 1, to 8 the use of local strategy
adaption still provides benefits over the no strategy
case but it is not as pronounced as in the single robot
test. The strategy parameter set (θ = 2.5, σ = 0.95)
is used for these simulation runs.
ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH BASED ON LOCAL COMMUNICATION
AND SENSING
339
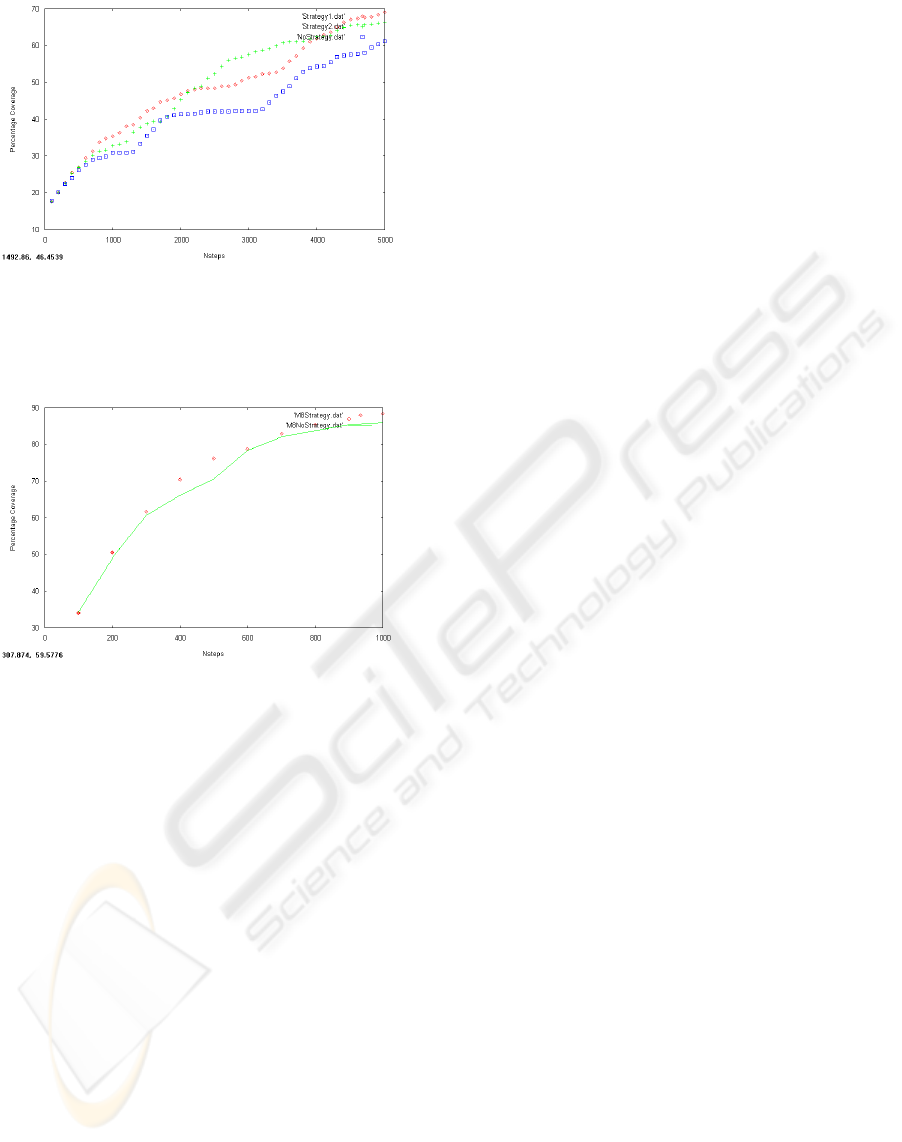
Figure 2: Single robot search on maze domain with n
x
=
70, n
y
= 70, r
seed
= 2392093, R
d
= 0.0, and σ = 0.75.
”NoStrategy.dat” does not apply local strategy selection.
”Strategy1.dat” and ”Strategy2.dat” both apply strategy se-
lection. Starting position is (55, 35).
Figure 3: Multi robot search using 8 robots on
box canyon domain with n
x
= 70, n
y
= 70,
r
seed
= 2392093, R
d
= 0.0, and σ =
0.95. Starting positions are ((10, 60), (10, 10), (60, 60),
(60, 10), (15, 60), (15, 10), (50, 60), (50, 10)).
5 CONCLUSION
A simulation model is presented which can simulate
multiple robots using stigmergy as a decentralized co-
ordination mechanism for solving foraging and do-
main coverage type tasks. The model is derived from
a biased random walk using localized decisions as
the basis of walker movement. It is scalable to any
number of robots and able to represent complex do-
mains/environments. This model can be used to study
the effect of random versus biased decision mak-
ing (based on weighted estimates of path suitability)
through a set of local control parameters which allow
experimentation with locally adaptive strategy selec-
tion. A set of simple tests is used to demonstrate some
of the model features. The model introduced here will
allow the study of optimal local strategy for move-
ment to be studied in detail in a series of experiments.
These more detailed experiments will be the subject
of future work.
REFERENCES
Anderson, R. (1988). Random-walk learning: A neu-
robiological correlate to trial-and-error, In: Neural
Networks and Pattern Recognition. Academic Press,
Boston.
Azar, Y., Broder, A., Karlin, A., Linial, N., and Phillips, S.
(1992). Biased random walks. In 24th Annual ACM
Symposium on Theory of Computing, pages 1–9.
Balch, T. and Arkin, R. (1994). communication in reac-
tive multiagent robotic systems. Autonmous Robots,
1(1):27–52.
Baltes, J. and Anderson, J. (2003). Flexible binary space
partitioning for robotic rescue. In Proc. Int. Conf.
IEEE IROS 2003 - Intelligent Robots and Systems.
Coppersmith, D. and Diaconis, P. (1987). Random walks
with reinforcements. Stanford Univ. Preprint.
Davis, B. (1990). Reinforced random walk. Prob. Th. Rel.
Fields, 84:203–229.
Glover, F. and Kochenberger, G. A. (2003). Handbook of
Metaheuristics. Kluwer publishing.
Gonzales-Banos, H. and Latombe, J. (2002). Navigation
strategies for exploring indoor environments. Int. J.
Robot. Res., 21(10-11):829–848.
Holland, O. and Melhuish, C. (1999). Stigmergy, self-
organization, and sorting in collective robotics. Ar-
tificial Life, 5:173–202.
Igel, C., Friedrichs, F., and Wiegand, S. (2005). Evolu-
tionary optimization of neural systems: The use of
strategy adaptation. In Trends and Applications in
Constructive Approximation, Int. Series of Numerical
Mathematics. Birkhuser Verlag.
Kaelbling, L., Cassandra, A., and Littman, M. (1994). Act-
ing optimally in partially observable stochastic do-
mains. In Twelfth National Conference on Artificial
Intelligence.
Lam, L. and Pochy, R. (1993). Active-walker models:
growth and form in non-equilibrium systems. Com-
putation simulation, 7:534.
Montgomery, J. and Randall, M. (2002). Anti-pheromone
as a tool for better exploration of search space. In
Third International Workshop on Ant Algorithms,
ANTS 2002.
Patterson, D. J. and Kautz, H. (2001). Autowalksat:a self-
tuning implementation of walksat. Electronic Notes in
Discrete Mathematics (ENDM), 9.
Rekleitis, I., Dudek, G., and Milios, E. (2001). Multi-robot
collaboration for robust exploration. Annals of Math-
ematics and Artificial Intelligence, 31(1-4):7–40.
Stachniss, C. and Burgard, W. (2003). Mapping and explo-
ration with mobile robots using coverage maps. In
Proc. of the IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS).
Wagner, I. A., Lindenbaum, M., and Bruckstein, A. M.
(1999). Distributed covering by ant-robots using evap-
orating traces. IEEE transactions on robotics and au-
tomation, 15(5).
ICINCO 2005 - ROBOTICS AND AUTOMATION
340
