
TRANSMISSION OF A MESSAGE DURING LIMITED TIME
WITH THE HELP OF TRANSPORT CODING
Evgenii Krouk
St.-Petersburg State University of Aerospace Instrumentation, Bolshaia Morskaia str., 67, St.-Petersburg, 190000, Russia
Sergei Semenov
Nokia Technology Platforms, P.O. Box 86, FIN-24101 Salo, Finland
Keywords: packet switching network, coding, transport protocols, telecommunication traffic, redundancy, message
delay, transport coding
Abstract: A fundamental characteristic of the majority of communications networks is the mean message delay. In a
packet-switching network, the mean packet and message delay may differ considerably from each other, and
their distribution will often take different forms. The mean message delay depends both on the mean packet
delay and on the dispersion of the packet delay. Obviously, by reducing the mean packet delay one can also
reduce the message delay. However, it is not always possible to decrease the mean packet delay in the
network. A proposed method of transmitting data in a network is based on the use of error-correcting
coding, which reduces the dispersion of the packet delay with some increase in the mean packet delay. The
conditions were obtained for which an increase in the mean packet delay with simultaneous reduction in the
dispersion leads to a reduction in the mean message delay. In many real time networks there are exist some
restrictions on the message delay. Use of the transport coding makes it possible to deliver the messages over
the network during some limited time with high probability.
1 INTRODUCTION
In this paper we will consider the applications of
error correcting codes to the data network. It is well
known, that using of error controlling codes adapted
to typical errors in a defended system is the
universal method of error protection. However in
modern data networks error correcting (or
controlling) codes are used only as means of
increasing the reliability of information during the
data transmission over the different channels; and no
correlation between coding and other network
procedures is considered. The application of coding
not only to the physical layer but also to the
procedures at higher layers (e.g. transport layer)
gives us some unexpected results indicating that
coding in network helps not only to increase the
reliability of the transmitted information, but also
can be used to improve such important characteristic
of a network, as the mean message delay. In this
chapter we will consider mostly the packet switching
network with datagram routing (or in datagram
mode). Packet switching is switching in which
messages are broken into packets and one packet at a
time is transmitted on a communication link. Thus,
when a packet arrives at a switching node on its path
to the destination site, it waits in a queue for its turn
to be transmitted on the next link in its path. The
datagram routing is packet switching in which each
packet finds its own path through the network
according to the current information available at the
nodes visited (Bertsekas, Gallager, 1992). To be
more precise, there is only one restriction on the
considered network model, which is essential for the
exposition of this chapter. This is the possibility to
get the packets out of order at the destination node.
It is shown in (Bertsekas, Gallager, 1992) that not
only the datagram networks but also the virtual
circuit networks have this feature as well. However,
for simplicity we assume that we are dealing with a
datagram network and that packets can get out of
order arbitrarily on the network consider a packet
switching network.
88
Krouk E. and Semenov S. (2005).
TRANSMISSION OF A MESSAGE DURING LIMITED TIME WITH THE HELP OF TRANSPORT CODING.
In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 88-93
DOI: 10.5220/0001419300880093
Copyright
c
SciTePress

The outline of the paper is as follows. Section 2
describes the concept of transport coding. Section 3
analyses the possibility of using transport coding for
improving the probability of message delivery
during limited time. Section 4 discusses an
interpretation of the results.
2 DECREASING THE MESSAGE
DELAY WITH THE HELP OF
TRANSPORT CODING
The one of the most important measure of the
effectiveness of a data network is the information
delay. The mean packet delay has been subject to
many studies, for example (Kleinrock, 1975),
(Kleinrock, 1964), (Kleinrock, Naylor, 1974).
However, in a packet-switching network, the
parameter of interest is not the delay of a separate
packet but the delay of a message as a whole. And
the mean message delay can differ from the mean
packet delay, as the assembly of a message at a
destination node can be delayed due to the absence
of a small number of packets (for example one).
This section deals with an analysis of the method of
decreasing the mean message delay with the help of
error-correcting code at the transport level of
network. This method was suggested in
(Kabatianskii, Krouk, 1993) and generalized in
(Krouk, Semenov, 2002). The possibility of using
error-correcting code in a bipolar network was
described in (Maxemchuk, 1975).
Let us consider a model of a network having M
channels, in which the capacity of the ith channel is
C
i
. The time taken to transmit a packet over a
channel has an exponential distribution with the
expectation
µ
1 . When the servicing device is busy,
the packet may be placed in a queue. Each message,
arriving in the network, is divided into
K
similar
packets. The length of each packet is
s
bits. The
traffic arriving in the network from external sources
forms a Poisson process with the intensity
γ
(packets per second). We will denote the mean
number of packets passing through the ith channel
per second by
i
λ
. The total network traffic is then
.
1
∑
=
=
M
i
i
λλ
,
(1)
If the packets arrive to a node via different
routes, we can assume that the dependence between
packet delays is negligible. Hence, the model of the
network turns out to be close to the Kleinrock
model, for which the Kleinrock «assumption of
independence» holds (Kleinrock, 1975), (Kleinrock,
1964). According to this assumption, the packet
delays can be regarded as independent random
variables. This statement was proved in
(Vvedenskaya, 1998) for some network types. Then
the ith channel can be represented in the form of a
queuing system with a Poisson flow of intensity
i
λ
at the input and an exponential servicing time with
mean
i
C⋅
µ
1
. In this case we can assume that the
packet delays in the network have an exponential
distribution with the expectation
),(
µ
λ
t , where
.
1
),(
1
ii
M
i
i
C
t
λµγ
λ
µλ
−
⋅=
∑
=
,
(2)
If we consider a case where all
M
channels
have the same carrying capacity while the external
traffic is uniformly distributed between the channels
(so that the intensity of the packet flow for all
channels is the same), expression (2) can be written
as follows:
,
1
1
),(
ρµ
µλ
−
⋅=
C
l
t
(3)
where
γ
λ
γ
λ
i
M
l
⋅
==
is the mean path length
traversed by a packet along the network,
C⋅
=
µ
λ
ρ
is the network load, and
∑
=
=
M
i
i
CC
1
is the overall
capacity of the network channels. The value of the
network load in this case is identical with the
i
i
i
C⋅
=
µ
λ
ρ
, the load of a single channel. In fact, as
it will be shown later, all needed assumptions are as
follows: the packet delays are independent random
variables with the exponential distribution and with
expectation of form
ρ
−1
a
, where
ρ
is the network
load and a is the constant for the given network.
The delay
T
of an uncoded message in the
network is determined by the maximum delay
among the
K
packets of the given message
TRANSMISSION OF A MESSAGE DURING LIMITED TIME WITH THE HELP OF TRANSPORT CODING
89

},,...,max{
1 K
ttT =
where
i
t is the delay of the ith packet of the
message; i.e., the message delay is equal to the delay
of the packet which arrives last. If we redenote the
packet delays of the message in increasing order
KKKK
ttt
::2:1
...≤≤≤ , we have
.
:KK
tT =
We can apply now the coding at the transport
level of the network and to encode the message,
which consists of K packets with the help of an
MDS (N, K) code (for example Reed-Solomon
code). In case of using the Reed-Solomon code each
of K packets is considered an element of a field
GF(2
s
) (s is the packet length), and after encoding
the original message consisting of K packets is
replaced by a message consisting of N packets.
When the encoded messages are transmitting over
the network, the traffic increases by a factor of 1/R
(R=K/N is the rate of the code used). This naturally
leads to an increase in the mean packet delay in the
network. However, at the node-addressee, to
reconstruct the message (in view of properties of
MDS codes), only K packets need to be received, as
against all N packets. We will show that with some
restrictions on the operation of the network this
method leads to a decrease of the mean message
delay. We will denote this method further on as
transport coding.
In case of using transport coding, the delay of the
encoded message is
.
:NKcod
tT
=
Using the apparatus of order statistics (David,
1981), the mathematical expectation of the delay of
the ith packet (for an overall number of packets
N )
can be written as follows:
[] [ ] [ ]
)()(1)(
1
:
tdPtPtPtBtE
iNi
iNi
−
∞
∞−
−
−⋅⋅⋅=
∫
(4)
or
[] [ ]
,1)(
1
1
0
1
:
duuuuPBtE
iN
i
iNi
−
−−
−⋅⋅⋅=
∫
(5)
where
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⋅=
1
1
i
N
NB
i
, )(tP is the distribution
function of packet delay and
)(
1
uP
−
is the inverse
function of
)(tP
. In the case of an exponential
distribution of the packet delay in the network
equations (4), (5) can be rewritten as follows:
∑
+−=
−
⋅=
N
iNj
Ni
jttE
1
1
:
][
(6)
where
t is the mean packet delay in the network
(depends on
λ
and
µ
). The mean delay of the
uncoded message in the network is then
TEt t j
KK
j
K
1
1
1
==⋅
−
=
∑
[](,)
:
λµ
(7)
where
),(
µ
λ
t is defined by (3). The sum on the
right-hand side of (7) can be represented as follows:
,
)1(...)1(2
1
ln
21
1
∑∑
∞
==
−
−+⋅⋅−⋅
−++=
i
i
K
j
iKKK
A
K
Kj
ε
∫
−−⋅⋅−⋅⋅=
1
0
,)1(...)1(
1
dxxixx
i
A
i
where
...577.0
=
ε
is Euler’s constant. Hence we
obtain the following estimate for the mean delay of
the uncoded message
1
T :
)ln(
1
1
)ln(),(
1
K
C
l
KtT +⋅
−
⋅=+⋅≥
ε
ρµ
εµλ
(8)
We can write the mean delay of the coded
message
2
T
for given
N , in accordance with (6), as
follows:
,),/(][
1
1
:2
∑
+−=
−
⋅==
N
KNj
NK
jRttET
µλ
(9)
where
),/(
µ
λ
Rt is the mean packet delay for traffic
that has been increased as a result of using coded
messages by a factor of
R1 ; R = K/N is the rate of
the code used. The sum on the right-hand side of (9)
can be represented as follows:
+
−
−+
⎟
⎠
⎞
⎜
⎝
⎛
−
=−=
∑∑∑
=
−
=
−−
+−=
−
N
j
KN
j
N
KNj
KNNKN
N
jjj
11
11
1
1
)(2
1
2
1
ln
≤
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
−
−+−−
+
∑
∞
=2
)1...()1)...((
i
ii
iNN
A
iKNKN
A
⎟
⎠
⎞
⎜
⎝
⎛
−
≤
KN
N
ln
(10)
ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES
90

0.2 0.4 0.6 0.8 1.0
0
2
4
6
8
10
12
14
K = 10, exact calculation
K = 10, estimation
K = 100, exact calculation
K = 100, estimation
T
1
/T
2
ρ
Figure 1: A gain of transport coding vs. network load.
It is possible to choose the code rate R in such a
way as to minimize the mean message delay
2
T . For
the best-chosen code, we obtain
.),/(min
/
1/
1
2
⎭
⎬
⎫
⎩
⎨
⎧
⋅=
∑
+−=
−
RK
KRKj
R
jRtT
µλ
(11)
Then, with the help of (10) we can estimate (9)
as
.
1
1
ln),/(min
2
⎭
⎬
⎫
⎩
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅≤
R
RtT
R
µλ
(12)
The mean packet delay for traffic which has been
increased by a factor of
R1 can be written in
accordance with (3), as
,),/(
ρµ
µλ
−
⋅=
R
R
C
l
Rt
(13)
where
γ
λ
γ
λ
==
R
R
l
is the mean path length
traversed by a packet along the network and
C⋅
=
µ
λ
ρ
is the load of the network when using the
uncoded messages. Minimizing (12) with respect to
R
, obtain
.
)1(
4
2
2
ρ
ρ
µ
−
⋅≤
C
l
T
(14)
The gain of using coding at the transport level of
the network can be obtained when the following
condition is satisfied:
0 200 400 600 800 1000
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
exact calculation
estimation
T
1
/T
2
K
Figure 2: A gain of transport coding vs. number of
information packets in message
.
.0
21
>−TT
(15)
Substituting (8) and (14) into (15), we obtain the
following condition for gain of using coding at
transport level
.
1
4
ln
ρ
ρ
ε
−
>+
K
(16)
The plots of gain of transport coding (in the
sense of decrease the mean message delay) are
shown in Fig. 1, 2.
As one can see from Fig. 1. exact calculation
shows that gain of transport coding can be obtained
with wider range of network load than it follows
from condition (16). However, the estimation
reflects the proper tend of changing gain versus
network load. The plot in Fig. 2 shows that increase
of number of information packets in message leads
to the gain increase that has logarithmic behaviour.
3 MESSAGE DELIVERY DURING
LIMITED TIME
For many data networks the probability )(
0
TP of
message delivery during the time no more than
0
T
has the same importance as the mean message delay.
Let us show that in this case transport coding also
can be used to increase
)(
0
TP . Let
{}
0
Pr Ttp
≤
=
denote the probability of message delivery during
the time no more than
0
T and let
R
p denote the
same probability for the encoded message having
regard to the increased network load. Then for the
uncoded messages we have
TRANSMISSION OF A MESSAGE DURING LIMITED TIME WITH THE HELP OF TRANSPORT CODING
91
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
K
P(To), PR(To)
P(To)
PR(To), N=K+1
PR(To), N=K+2
PR(To), N=K+10
Figure 3: A probability of message delivery during time T
0
vs. number of information packets in message, a = 4, ρ =
0.2
.
K
pTP =)(
0
(17)
and in case of using the encoded messages (code
length is N) the probability
)(
0
)(
TP
R
that the
encoded message is delivered during the time no
more than
o
T can be written as follows
()
PT
N
i
pp
R
R
i
i
NK
R
Ni()
()
0
0
1=
⎛
⎝
⎜
⎞
⎠
⎟
⋅− ⋅
=
−
−
∑
(18)
Now if we will use the same assumptions as in
Section 1 about exponential distribution of packet
delay and about dependence of the mean packet
delay on the network load (3) we obtain the
following expression for p:
pe
Tt
=−
−
1
0
/( ,)
λµ
(19)
where
t(, )
λ
µ
is the mean packet delay defined by
(3). Let denote as a the ratio
Tt
0
/(,)
λ
µ
and as
ξ
the ratio of the mean packet delay in the ordinary
network without transport coding to the mean packet
delay in the network with transport coding,
ξλµλµ ρ ρ
==−−
−
ttR R(, ) (/ , ) ( )( )11
1
. Then
formulas (17) and (18) can be rewritten as follows:
()
K
a
eTP
−
−= 1)(
0
(20)
()
PT
N
i
ee
Ra
Ni
i
NK
ia()
()
0
0
1=
⎛
⎝
⎜
⎞
⎠
⎟
⋅− ⋅
−
−
=
−
−
∑
ξξ
(21)
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
K
P(To), PR(To)
P(To)
PR(To), N=K+1
PR(To), N=K+2
PR(To), N=K+10
Figure 4: A probability of message delivery during time T
0
vs. number of information packets in message, a = 4, ρ =
0.6
.
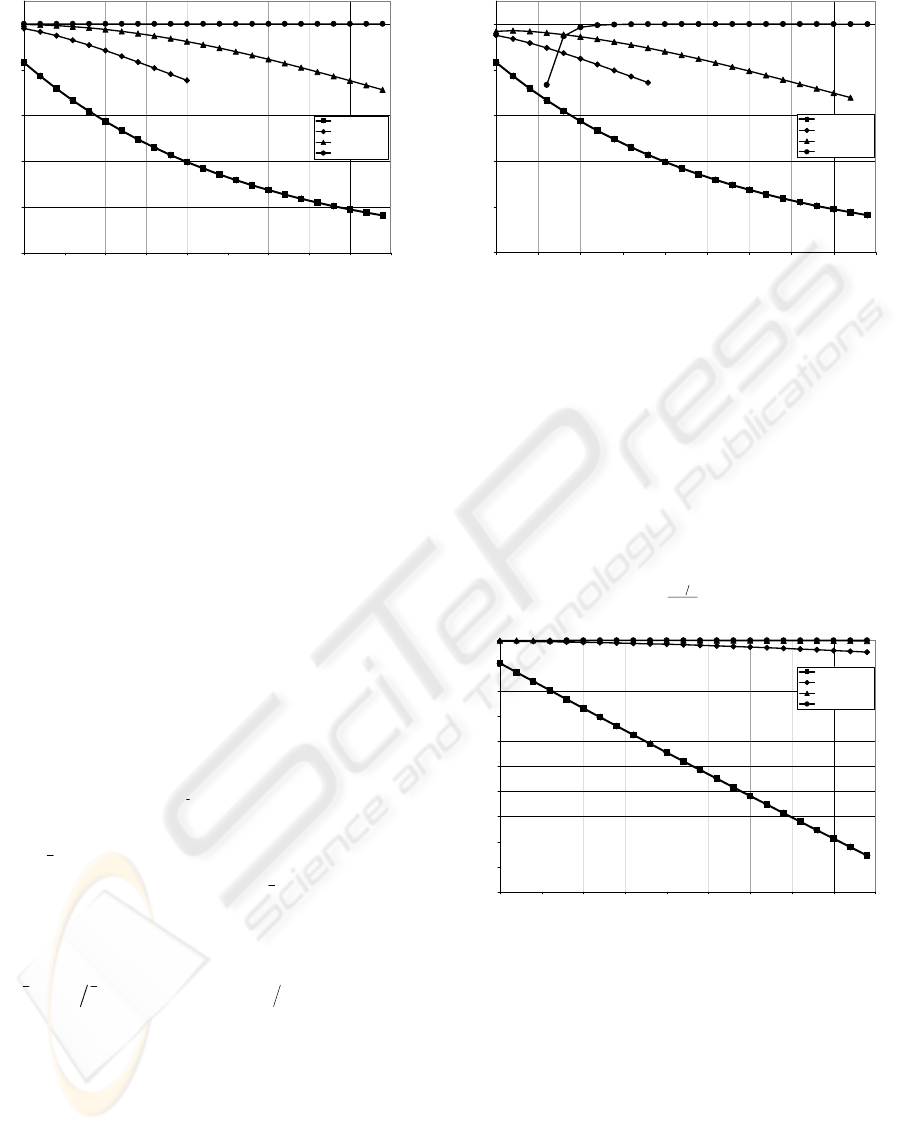
It is easy to verify that
0)(
0
→TP with
increasing the number of packets in the message K.
From the other hand, in case
ξ
a
eR
−
>− )1( ,
cTP
R
→)(
0
)(
,
)10(
≤
<
c
with increasing K. The
condition
ξ
a
eR
−
>− )1( with the restriction
ρ
>R
can be written as the following inequality
ρ
ρ
ρ
<<−
−
−
−
Re
a
R
1
1
1
.
(22)
0.9
0.91
0.92
0.93
0.94
0.95
0.96
0.97
0.98
0.99
1
10 20 30 40 50 60 70 80 90 100
K
P(To), PR(To)
P(To)
PR(To), N=K+1
PR(To), N=K+2
PR(To), N=K+10
Figure 5: A probability of message delivery during time T
0
vs. number of information packets in message, a = 7, ρ =
0.6
.
Thus, for any R satisfying (22) the addition of N-
K redundant packets to the message leads to the fact
that the probability
)(
0
)(
TP
R
tends to the constant
greater than zero, whilst the probability
)(
0
TP tends
to zero with increasing K. The plots of
)(
0
TP and
)(
0
)(
TP
R
against K are represented in Fig. 3 - 5.
ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES
92

4 CONCLUDING REMARKS
The given estimates of mean message delays in the
network are rather rough. However, even these
estimations show that transport coding leads to a
significant decrease of mean message delay under
conditions of moderate network load. Moreover, it is
possible to use transport coding not only to decrease
the mean message delay, but also to increase the
reliability of message delivery during limited time,
which also is a question of great interest. All given
estimations and exact formulas given are based on
the assumption that packet delay in a network has an
exponential distribution. Although this assumption
has some grounding in (Kleinrock, 1975),
(Vvedenskaya, 1998) for many kinds of networks, it
is possible that in some networks the distribution of
the packet delay differs from the exponential one.
However, this assumption was used only for the
simplification of calculations. It is necessary to note
that an exponential distribution of packet delay is
not the best case for use of transport coding because
the probability of a high packet delay is very small.
We can therefore expect that the gain of transport
coding could be more significant for another
distribution of packet delay.
REFERENCES
Bertsekas, D., Gallager, R., 1992, Data Networks. Prentice
Hall.
Kleinrock, L., 1975, Queuing Systems. Theory, vol.1, John
Wiley & Sons.
Kleinrock, L., 1964, Communication nets; stochastic
message flow and delay. N.Y., Dover.
Kleinrock, L., Naylor, W., 1974, On Measured Behavior
of the ARPA Network, AFIPS Conf. Proc., National
Computer Conf., vol. 43, pp. 767-780.
Kabatianskii, G.A., Krouk, E.A., 1993, Coding Decreases
Delay of Messages in Networks. IEEE International
Symposium on Information Theory. Proceedings.
Maxemchuk, N.F., 1975, Dispersity routing, IEEE Conf.
Commun., San Francisco, 1975, N.Y., vol. 3.
David, H.A., 1981, Order statistics, .1, John Wiley &
Sons.
Vvedenskaya, N.D., 1998, Large Queuing System where
Messages are Transmitted via Several Routes,
Problems Of Information Transmission, Vol. 34, Nmb.
2, April–June, pp. 180–189
Krouk, E., Semenov, S., 2002, Application of Coding at
the Network Transport Level to Decrease the Message
Delay. Proceedings of Third International Symposium
on Communication Systems Networks and Digital
Signal Processing. 15-17 July 2002 Staffordshire
University, UK, pp. 109-112.
TRANSMISSION OF A MESSAGE DURING LIMITED TIME WITH THE HELP OF TRANSPORT CODING
93
