
LINEAR QUADRATIC GAUSSIAN REGULATORS FOR
MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS
L. Armesto and J. Tornero
Dept. of Systems Engineering and Control, Technical University of Valencia,
Camino de Vera s/n 46022, Valencia, Spain
Keywords:
Multi-rate Sampled Data Systems, Linear Quadratic Regulator, Kalman Filter.
Abstract:
In this paper, linear quadratic Gaussian regulators are presented and formalized for multi-rate sampled-data
stochastic systems using two well-known approaches: lifting technique and time-variant periodic modeling. It
has been demonstrated that both regulators are equivalent at the global frame-period with different computa-
tional costs and execution periods. An interesting analysis has been done to demonstrate the convergence of a
periodic Kalman filter, used in the periodic regulator, into its equivalent continuous one (Bucy Kalman filter),
when the periodicity ratio converges to infinity. In addition to this, in both regulators, multi-rate holds have
been used, acting as interfaces between signals at different sampling rates, which may improve the system
performance. A numerical example of LQG multi-rate control of a MIMO plant shows the application of both
regulators, where in addition to showing the improvement with respect to the single-rate case.
1 INTRODUCTION
In complex real-time control systems, it becomes
more and more realistic to assume different sampling
periods for different system variables. This is the case
of many distributed control systems, where there are
more than one processor and many communication
channels involved. Moreover, sensor and actuators
with different dynamics should be treated at different
rates. For all these situations, multi-rate techniques
may be used to improve system performances.
In multi-rate sampled-data systems, inputs and out-
puts are updated at different sampling rates. In most
of the cases, multi-rate sampling is due to technolog-
ical limitations in sensors and actuators. Other lim-
itations may come from computational requirements
in real-time applications such as multi-rate sensor fu-
sion, data-missing, mapping, etc.
A general multi-rate sampling could be asynchro-
nous and totally random, although it is generally ac-
cepted that a periodicity between sampling-rates of
inputs and outputs exists. On the one hand, the m
inputs are updated at T
u
v
, with v = 1, 2, . . . , m; on
the other hand, the p outputs are sampled at T
y
w
,
with w = 1, 2, . . . , p. The frame-period is for-
mally defined as
¯
T = lcm(T
u
v
, T
y
w
) which involves
all input and output periods, and the base-period is
T = gcd(T
u
v
, T
y
w
). The ration between periods is
N =
¯
T /T , where N is the periodicity of the system.
Therefore, inputs and outputs are updated/sampled at
multiple time instants of the base-period, with T
u
v
=
N
u
v
·T and T
y
w
=N
y
w
·T .
The multi-rate problem has been extensively
treated in the last four decades and it is possible
to find many contributions dealing with modeling
and analysis (Albertos, 1990; Araki and Yamamoto,
1986; Godbout et al., 1990; Khargonekar et al., 1985;
Tornero, 1985; Tornero and Armesto, 2003; Tornero
et al., 1999), as well as control design of multi-rate
systems (Chen and Francis, 1995; Colaneri and de
Nicolao, 1995; Qui and Chen, 1999; Tangirala et al.,
1999). One of the approaches to treat the modeling
phase is to assume an enlarged MIMO system (Khar-
gonekar et al., 1985; Albertos, 1990; Araki and Ya-
mamoto, 1986; Godbout et al., 1990). In these ap-
proaches, a discrete time-invariant state equation ex-
pressed at frame period
¯
T is used, with enlarged in-
put and output vectors. Many of these modeling tech-
niques are based on the initial idea of VSD (Kranc,
1957). In (Tornero, 1985), Tornero proposed an in-
teresting time-variant modeling technique for multi-
rate systems expressed at base-period T , based on two
auxiliary state vectors associated to inputs and out-
puts. In this approach, usually periodic, input and
67
Armesto L. and Tornero J. (2006).
LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 67-74
DOI: 10.5220/0001209000670074
Copyright
c
SciTePress
output sampling hold mechanisms are represented by
two periodic and diagonal matrices. In (Tornero and
Armesto, 2003), it is demonstrated that the approach
is equivalent to many other well-known multi-rate
modeling techniques.
In this paper, we focus on multi-rate linear
quadratic Gaussian regulators, which has been pre-
viously treated in (Colaneri and de Nicolao, 1995;
Tornero et al., 1999). In (Lee and Tomizuka, 2003),
a Kalman filter is developed using the lifting tech-
nique. Shah et. al. (Shah et al., 1995) implemented a
multi-rate formulation of the iterated EKF on a biore-
actor. Kalman filters have also been used in multi-
rate digital signal processing and filter banks (analy-
sis/synthesis) (Hong, 1994). In (Zhang et al., 2004) a
Kalman filter is obtained based on It
ˆ
o-Volterra equa-
tions for continuous, multi-rate and randomly sam-
pled measurements.
Techniques applied for multi-rate Kalman filter
have been also extended to non-linear multi-rate filter-
ing such as the Extended and Unscented Kalman fil-
ters (Julier et al., 2000; Julier and Uhlmann, 2002). In
this sense, different multi-rate sensor fusion applica-
tions in mobile robotics have been already presented
(Armesto et al., 2004; Armesto and Tornero, 2004).
In the paper, two different but equivalent multi-
rate LQG regulators are presented, based on perio-
dic (time-variant) and on lifting techniques (time-
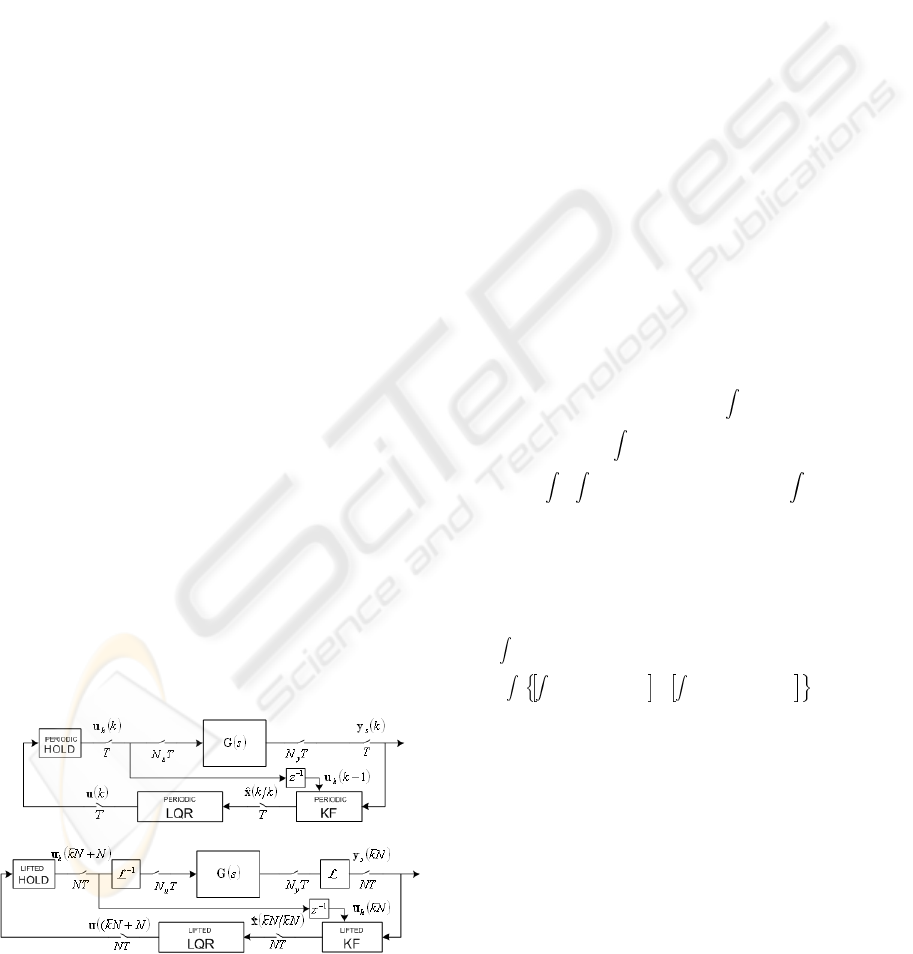
invariant), which can be summarized in figure 1. One
of the most important contributions comes from the
fact that multi-rate holds are integrated into LQG reg-
ulators. Another contribution is the demonstration
of convergence of discrete-time Kalman filter to the
continuous one (Bucy-Kalman), when the periodic-
ity ratio goes to infinity. In addition, multi-rate holds
are defined according to general primitive functions,
which can generate conventional ZOH and FOH as
well as others holds based on Bezier, exponential or
sinusoidal functions (Armesto and Tornero, 2003).
Figure 1: Multi-rate LQG control structures.
2 MULTI-RATE TIME-VARIANT
PERIODIC LINEAR
QUADRATIC GAUSSIAN
REGULATOR
2.1 Sampled-data System Model
Suppose a continuous-time stochastic system:
˙x(t)=A
c
·x(t)+B
c
·u(t)+G
c
·w(t)
y(t) =C·x(t)+v(t)
where A
c
∈ ℜ
n×n
is the state matrix, B
c
∈ ℜ
n×m
in-
put matrix and C ∈ ℜ
p×n
output matrix, being n, m
and p the dimensions of the state x(t), input u(t) and
output y(t), respectively; G
c
∈ ℜ
n×g
is the system
noise transmission matrix, coupling the system noises
with the state; w (t) ∈ ℜ
g×1
and v(t) ∈ ℜ
p×1
are inde-
pendent Gaussian Wiener processes with covariances
Q
c
∈ ℜ
g×g
and R
c
∈ ℜ
p×p
, respectively.
The sampled-data system with discrete inputs at
base period is (Loan, 1978):
x((k+1)T )=A(T)·x(kT )+B(T )·u(kT )+w(kT )
(1)
y(kT )=C·x(kT )+v(kT ) (2)
with,
A =A(T ) =e
A
c
T
B =B(T ) =
T
0
e
A
c
(T−τ )
B
c
dτ
w(kT ) =
T
0
e
A
c
(T−τ )
G
c
w(τ −kT )dτ
v(kT ) =C
T
0
t
0
e
A
c
(T−τ )
G
c
dw(τ −k T )dt+
T
0
dv(τ −kT )
In the remainder of the paper, we use notation x(k)=
x(kT ), u(k) = u(kT ), y(k) = y(kT ), w(k) =
w(kT ) and v(k) = v(kT ), with discrete covariances
Q=Q(T ) and R =R(T ) computed as (Colaneri and
de Nicolao, 1995),
Q =
T
0
e
A
c
(T−τ )
·G
c
·Q
c
·G
T
c
·e
A
T
c
(T−τ )
dτ
R =C
T
0
T
τ
e
A
c
(s−τ)
G
c
ds
Q
c
T
τ
G
T
c
e
A
T
c
(s−τ)
ds
dτ C
T
+R
c
T
2.2 Multi-rate Time-Variant
Periodic High Order Holds
Multi-rate high-order holds (MR-HOH) are used
as multi-rate interfaces between signals at differ-
ent sampling frequencies (Tornero and Tomizuka,
2002). Low-frequency signals are extrapolated to
high frequency, usually at base-period. In (Armesto
and Tornero, 2003), it was proposed a methodol-
ogy for designing MR-HOHs based on primitive
functions such as polynomial extrapolation, approx-
imation functions (Bezier) and even non-polynomial
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
68

Table 1: Multi-rate High Order Holds Based on Polynomial
Extrapolation Functions.
Name Order Primitive function u
h
(t)
ZOH 0 u(t
j
)
FOH 1 1+
t−t
j
t
j
−t
j−1
·u(t
j
)−
t−t
j
t
j
−t
j−1
·u(t
j−1
)
NOH n
n
l=0
n
q=0
q6=l
t − t
j−q
t
j−l
− t
j−q
· u(t
j−l
)
Table 2: Multi-rate High Order Holds Based on Polynomial
Extrapolation Discrete Functions.
Name Order Primitive function u
h
(t)
ZOH 0 u(jN
u
T )
FOH 1 1+
i
N
u
·u(jN
u
T )−
i
N
u
·u((j −1)N
u
T )
NOH n
n
l=0
n
q=0
q6=l
i + qN
u
(q − l)N
u
· u((j − l)N
u
T )
functions (exponential, sinusoidal, etc). In (Kabamba,
1987), other Generalized Sampled-data Hold Func-
tions (GSHF) can be found.
Multi-rate sampled-data systems are obtained com-
bining different MR-HOH and the continuous-time,
providing different system performance (Braslavsky
et al., 1998).
In Table 1 it can be found the primitive functions
for polynomial extrapolation functions used to gener-
ate conventional ZOH, FOH and even the general case
NOH (N-th Order Hold).
Primitive functions use signal samples at low fre-
quency as control point for generating an extrapolated
continuous-time signal,
u
h
(t) =
n
l=0
f
n,l
(t, t
j
, t
j−1
, . . . , t
j−l
)·u(t
j−l
) =
n
l=0
f
n,l
(·)u(t
j−l
)
where n is the order of the hold device and t
j
is the
time of the last updated input, with t
j
≤ t < t
j+1
.
The discrete function expressed at base-period with
regular sampling is,
u
h
(k ) =
n
l=0
f
∗
n,l
(i, N
u
) · u((j−l)N
u
T )
where t
j
= j · N
u
· T , t
j
− t
j−1
= N
u
and i =
Mod(k, N
u
) = k − jN
u
. Table 2 shows the signal
sampled at high frequency for ZOH, FOH and NOH.
In order to describe the multi-rate input sampling
at base-period, a periodic diagonal matrix is defined
(Tornero, 1985),
∆
u
(k ) = diag{δ
u
v
(k ), v = 1, 2, . . . , m}
δ
u
v
(k ) =
1 if Mod(k, N
u
v
)= 0
0 otherwise
According to this, the periodic representation for
multi-rate high-order holds (Armesto and Tornero,
2003) is ,
υ
u
(k+1) = A
h
(k )·υ
u
(k )+B
h
(k )·u(k) (3)
u
h
(k ) = C
h
(k )·υ
u
(k )+D
h
(k )·u(k) (4)
where υ
u
(k) is an auxiliary state vector related to the
input hold mechanism. The periodic multi-rate hold
matrices are defined as,
A
h
(k) =
I−∆
u
(k) 0 . . . 0
∆
u
(k) I−∆
u
(k) . . . 0
.
.
.
.
.
.
.
.
.
.
.
.
0 . . . ∆
u
(k) I− ∆
u
(k)
B
h
(k) =
∆
u
(k)
0
.
.
.
0
C
h
(k) =
f
∗
n,0
(·) f
∗
n,1
(·) . . . f
∗
n,n
(·)
• [I−∆
u
(k)]D
h
(k) = ∆
u
(k)
Despite of the mathematical complexity, the perio-
dic state-space representation for a MR-ZOH is sim-
ply,
υ
u
(k+1) = (I−∆
u
(k ))·υ
u
(k )+∆
u
(k )·u(k)
u
h
(k ) = (I−∆
u
(k ))·υ
u
(k )+∆
u
(k )·u(k)
which means that the input u(k) is incorporated into
the state on every update (at low frequency) and the
output u
h
(k) maintains this value until the next up-
date. For a MR-FOH the formulation is,
υ
u
(k+ 1)
υ
u
(k− N
u
+1)
=
I−∆
u
(k) 0
∆
u
(k) I−∆
u
(k)
·
υ
u
(k)
υ
u
(k− N
u
)
+
∆
u
(k)
0
u(k)
u
h
(k)=
1+
i
N
u
−
i
N
u
• [I−∆
u
(k)]
υ
u
(k)
υ
u
(k− N
u
)
+∆
u
(k)u(k)
where • represents the inner product. In this case,
the present updated input and the last updated input
are stored in the state and used to generate a ramp
based on these values at the output. In section 3.1
it is shown a very simple numerical example of the
transfer function of several holds.
2.3 Multi-rate Time-Variant
Periodic Stochastic System
A general multi-rate periodic stochastic system can
be seen as the concatenation of a multi-rate high or-
der hold (3) and (4) and the discrete-time stochastic
model (1) and (2) at base-period. Note that, we have
expressed the multi-rate stochastic system in terms of
k instead of k + 1 because the LQG requires the es-
timation of x(k) in real-time, that is at the present
sampling period k,
x(k ) = A·x(k−1)+B·u
h
(k−1)+w(k−1) (5)
y
s
(k ) = C
s
(k )·x(k)+ v
s
(k ) (6)
where y
s
(k) only contains measured outputs, C
s
(k)
is the row-reduced matrix of C and v
s
(k) is the re-
duced noise vector, respectively. In the remainder of
the paper, matrices and vectors affected by the multi-
rate sampling will be also denoted with sub-index s.
The size-varying output vector is defined as,
y
w
(k ) ⊂ y
s
(k )∈ ℜ
p(k)×1
if δ
y
w
(k ) = 1
δ
y
w
(k ) =
1 if Mod(k, N
y
)= 0
0 otherwise
being p(k) the number of sampled outputs at a given
time instant k. In fact, the complete state-space repre-
sentation of the multi-rate system including the hold
is,
x
MR
(k) = A
MR
(k−1)x
MR
(k−1)+B
MR
(k−1)u(k−1)+
w(k−1)
0
y
s
(k) = C
MR
(k)·x
MR
(k)+ v
s
(k)
LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS
69

where x
MR
(k) = [x(k) υ
u
(k)]
T
and,
A
MR
(k) =
A BC
h
(k)
0 A
h
(k)
B
MR
(k) =
BD
h
(k)
B
h
(k)
C
MR
(k) = [C
s
(k) 0]
2.4 Multi-rate Time-Variant
Periodic Kalman Filter
According to the periodic multi-rate stochastic system
(5) and (6), we define the periodic estimation model,
ˆx(k|k −1) = A·ˆx(k−1|k −1)+B·u
h
(k−1)
ˆx(k|k) = ˆx(k|k−1)+K
s
(k)·(y
s
(k)−C
s
(k)·ˆx(k|k−1))
Note that the state of the hold is not included, since
it is completely known. Therefore, input of the esti-
mation model is the output of the hold. In this sense,
equations related with the Kalman Gain K
s
(k) and
output covariance matrix S
s
(k) are affected by the
multi-rate output sampling, while the equation related
with the state covariance prediction P(k|k−1) is not
affected. Therefore, the multi-rate periodic Kalman
filter (MR-PKF) equations are,
P(k |k−1) =A·P(k−1|k−1)·A
T
+Q
K
s
(k ) = P(k|k−1)·C
T
s
(k )·S
−1
s
(k )
S
s
(k ) = C
s
(k )·P(k|k−1)·C
T
s
(k )+R
s
(k )
P(k |k)= P(k|k−1) − K
s
(k )·C
s
(k )·P(k|k−1)
Special attention requires the case p(k) = 0, where
outputs are not sampled. The output vector is void and
also each vector/matrix denoted with sub-index s. It
is not possible to correct the state and its covariance,
and they both are simply predicted.
2.5 Multi-rate Time-Variant
Periodic Linear Quadratic
Regulator
Suppose a single-rate index as follows,
J
SR
=
1
2
∞
k=0
x
T
(k ) u
T
(k )
·
˜
Q
˜
M
˜
M
T
˜
R
·
x(k )
u(k)
(7)
with
˜
Q,
˜
M and
˜
R weighting matrices for states
and inputs previously computed from a discrete-time
continuous-time index,
J
c
=
1
2
∞
0
x
T
(t) u
T
(t)
·
Q
c
0
0 R
c
·
x(t)
u(t)
dt (8)
with,
˜
Q =
T
0
e
A
T
c
t
˜
Q
c
e
A
c
t
dt
˜
M =
T
0
e
A
T
c
t
˜
Q
c
t
0
e
A
c
τ
B
c
dτ
dt
˜
R =
T
0
t
0
B
T
c
e
A
T
c
τ
dτ
˜
Q
c
t
0
e
A
c
τ
B
c
dτ
dt+
˜
R
c
·T
The multi-rate periodic equivalent index to the
single-rate one considering the hold is,
J
MR
=
1
2
∞
k=0
[x
T
(k) u
T
h
(k)]
˜
Q
˜
M
˜
M
T
˜
R
x(k)
u
h
(k)
=
1
2
∞
k=0
[x
T
MR
(k) u(k)]
Q
MR
(k) M
MR
(k)
M
T
MR
(k) R
MR
(k)
x
MR
(k)
u(k)
where,
Q
MR
(k) =
˜
Q
˜
MC
s
(k)
C
T
s
(k)
˜
M C
T
s
(k)
˜
RC
s
(k)
M
MR
(k) =
˜
MD
h
(k)
C
T
s
(k)
˜
RC
s
(k)
R
MR
(k) = D
T
h
(k)
˜
RD
h
(k)
The optimal multi-rate control input is obtained
from the solution of the N-Periodic Riccati equation
(Tornero et al., 1999),
˜
A
MR
(k ) = A
MR
(k )−B
MR
(k )·R
−1
MR
(k )·M
T
MR
(k )
S
MR
(k ) =
˜
A
MR
T
(k )·S
MR
(k+1)·[
˜
A
MR
(k )+K
MR
(k ))]+
+Q
MR
(k )−M
MR
(k )·R
−1
MR
(k )·M
T
MR
(k )
K
MR
(k ) = [R
MR
(k )+B
T
MR
(k )·S
MR
(k+1)·B
MR
(k )]
−1
·
· B
MR
(k )·S
MR
(k+1)·
˜
A
MR
(k )
u(k)= −(R
−1
MR
(k )·M
T
MR
(k )+K
MR
(k ))·x(k)
Remark 1 R
MR
(k) is singular if non one input is up-
dated. This apparent problem can be solved since el-
ements related with non updated inputs do not affect
to the index (Colaneri and de Nicolao, 1995).
3 MULTI-RATE LIFTED LINEAR
QUADRATIC GAUSSIAN
REGULATOR
3.1 Multi-rate Lifted High Order
Holds
The lifting technique for the dual-rate HOH gives the
lifted transfer function expressed at frame-period,
¯
G
h
(¯z) =[I
n
l=0
f
∗
n,l
(1) · ¯z
−l
. . .
n
l=0
f
∗
n,l
(N − 1) · ¯z
−l
]
T
where inputs are updated once per frame-period. This
transfer function is derived from the state-space rep-
resentation is as follows,
¯υ
u
(
¯
kN +N)=
¯
A
h
·¯υ
u
(
¯
kN)+
¯
B
h
·¯u(
¯
kN)
¯u
h
(
¯
kN) =
¯
C
h
·¯υ
u
(
¯
kN)+
¯
D
h
·¯u(
¯
kN)
where,
¯
G
h
(¯z) =
¯
C
h
¯zI −
¯
A
h
−1
¯
B
h
+
¯
D
h
¯
A
h
=
0 0 . . . 0
I 0 . . . 0
.
.
.
.
.
.
.
.
.
.
.
.
0 . . . I 0
¯
B
h
=
I
0
.
.
.
0
¯
C
h
=
0 . . . 0 0
f
∗
n,1
(1) . . . f
∗
n,n
(1) 0
.
.
.
.
.
.
.
.
.
.
.
.
f
∗
n,1
(N −1) . . . f
∗
n,n
(N −1) 0
¯
D
h
=
I
f
∗
n,0
(1)
.
.
.
f
∗
n,0
(N −1)
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
70

Table 3: Numerical Examples of Lifted Transfer Function
of MR-HOHs.
N DR-ZOH DR-FOH DR-SOH
1 G
h
= 1 G
h
= 1 G
h
= 1
2 G
h
=
1
1
G
h
=
1
3¯z−1
2¯z
G
h
=
1
15¯z
2
−10¯z+3
8¯z
2
3 G
h
=
1
1
1
G
h
=
1
4¯z−1
3¯z
5¯z−2
3¯z
G
h
=
1
14¯z
2
−7¯z+2
9¯z
2
20¯z
2
−16¯z+5
9¯z
2
Lifted MR-HOH for a periodic sampling can be ob-
tained using successive substitution of equation (3)
and (4). In that case, the lifted input vector is ¯u(
¯
kN)=
[u
T
(
¯
kN−N) . . . u
T
(
¯
kN−2N
u
) u
T
(
¯
kN−N
u
)]
T
. In
order to show that despite of the mathematical com-
plexity the implementation of MR-HOH is very sim-
ple, since at the end they are composed with simple
transfer functions. In this sense, table 3 shows the
lifted transfer functions of ZOH, FOH and SOH.
3.2 Multi-rate Lifted Stochastic
System
A general multi-rate lifted stochastic system is ob-
tained by combining multi-rate holds with the sto-
chastic system,
¯x(
¯
kN ) =
¯
A· ¯x((
¯
k−1)N)+
¯
B· ¯u
h
(
¯
kN )+
¯
G· ¯w(
¯
kN )
¯y
s
(
¯
kN ) =
¯
C
s
·¯x((
¯
k−1)N)+
¯
D
s
·¯u
h
(
¯
kN )+
˜
G
s
· ¯w(
¯
kN )+¯v
s
(
¯
kN )
with lifted signals,
¯w(
¯
kN) =[w
T
(
¯
kN −N) . . . w
T
(
¯
kN −2) w
T
(
¯
kN −1)]
T
¯y
s
(
¯
kN) = [y
T
(
¯
kN −N +N
y
) . . . y
T
(
¯
kN −N
y
) y
T
(
¯
kN)]
T
¯v
s
(
¯
kN) = [v
T
(
¯
kN −N +N
y
) . . . v
T
(
¯
kN −N
y
) v
T
(
¯
kN)]
T
and,
¯
A = A
N
¯
B =
A
N−1
·B A
N−2
·B . . . B
¯
G =
A
N−1
A
N−2
. . . I
¯
C
s
=
C·A
N
y
C·A
2N
y
.
.
.
C·A
N
¯
D
s
=
C·B 0 . . . 0
C·A
N
y
·B C·B . . . 0
.
.
.
.
.
.
.
.
.
.
.
.
C·A
N−N
y
·B C·A
N−2N
y
·B . . . C·B
˜
G
s
=
C 0 . . . 0
C·A
N
y
C . . . 0
.
.
.
.
.
.
.
.
.
.
.
.
C·A
N−N
y
C·A
N−2N
y
. . . C
In fact, the complete state-space representation, in-
cluding the hold, is:
¯x
MR
(
¯
kN ) =
¯
A
MR
¯x
MR
((
¯
k−1)N )+
¯
B
MR
¯u(
¯
kN )+
¯
G ¯w(
¯
kN )
0
¯y
s
(
¯
kN ) =
¯
C
MR
¯x
MR
((
¯
k−1)N )+
¯
D
MR
¯u(
¯
kN )+
˜
G
s
¯w(
¯
kN )+¯v
s
(
¯
kN )
where ¯x
MR
(
¯
kN) = [¯x(
¯
kN) ¯υ
u
(
¯
kN)]
T
and,
¯
A
MR
=
¯
A
¯
B·
¯
C
h
0
¯
A
h
¯
B
MR
=
¯
B·
¯
D
h
¯
B
h
¯
C
MR
=
¯
C
s
¯
D
s
·
¯
C
h
¯
D
MR
=
¯
D
s
·
¯
D
h
3.3 Multi-rate Lifted Kalman Filter
(MR-LKF)
The lifted estimation model is,
ˆ
¯x(
¯
kN |(
¯
k−1)N )=
¯
A·
ˆ
¯x((
¯
k−1)N |(
¯
k−1)N )+
¯
B·¯u
h
(
¯
kN )
ˆ
¯x(
¯
kN |
¯
kN ) =
ˆ
¯x(
¯
kN |(
¯
k−1)N )+
+
¯
K
s
(
¯
kN )·(¯y
s
(
¯
kN )−
¯
C
s
·
ˆ
¯x((
¯
k−1)N |(
¯
k−1)N )−
¯
D
s
·¯u(
¯
kN ))
where
¯
K
s
(
¯
kN) is the Kalman correction matrix. Once
again, the state of the hold is not estimated since it is
assumed to be completely known.
Kalman filter equations for the lifted model are,
¯
P(
¯
kN |(
¯
k−1)N) =
¯
A·
¯
P((
¯
k−1)N|(
¯
k−1)N)·
¯
A
T
+
¯
G·
¯
Q·
¯
G
T
¯
P
xy,s
(
¯
kN |(
¯
k−1)N) =
¯
C
s
¯
P((
¯
k−1)N|(
¯
k−1)N)
¯
A
T
+
˜
G
s
¯
Q
¯
G
T
¯
P
yy,s
(
¯
kN ) =
¯
C
s
¯
P((
¯
k−1|)N|(
¯
k−1|)N)
¯
C
T
s
+
˜
G
s
¯
Q
˜
G
T
s
+
¯
R
s
¯
K
s
(
¯
kN ) =
¯
P
T
xy,s
(
¯
kN |(
¯
k−1)N)·
¯
P
−1
yy,s
(
¯
kN ) (9)
¯
P(
¯
kN |
¯
kN ) =
¯
P(
¯
kN |(
¯
k−1)N)−
¯
K
s
(
¯
kN )·
¯
P
xy,s
(
¯
kN |(
¯
k−1)
where the enlarged covariance matrices are,
¯
Q = E[ ¯w(
¯
kN)· ¯w
T
(
¯
kN)]
¯
R
s
=E[¯v
s
(
¯
kN)·¯v
T
s
(
¯
kN)]
3.4 Multi-rate Lifted Linear
Quadratic Regulator
The multi-rate lifted equivalent index to the single-
rate one (8) considering the hold is,
¯
J
MR
=
1
2
∞
¯
k=0
[¯x
T
MR
(
¯
kN ) ¯u
T
(
¯
kN )]·
¯
Q
MR
¯
M
MR
¯
M
T
MR
¯
R
MR
·
¯x
MR
(
¯
kN )
¯u(
¯
kN )
where,
¯
Q
MR
¯
M
MR
¯
M
T
MR
¯
R
MR
=
¯
˜
A 0 0
0
¯
˜
B
¯
C
h
¯
˜
B
¯
D
h
T
¯
˜
Q
¯
˜
M
¯
˜
M
T
¯
˜
R
¯
˜
A 0 0
0
¯
˜
B
¯
C
h
¯
˜
B
¯
D
h
with,
¯
˜
Q=diag{
˜
Q, . . . ,
˜
Q}
¯
˜
M=diag{
˜
M, . . . ,
˜
M}
¯
˜
R=diag{
˜
R, . . . ,
˜
R}
¯
˜
A =
I
A
.
.
.
A
N
¯
˜
B =
0 . . . 0 0
B . . . 0 0
.
.
.
.
.
.
.
.
.
0
A
N−1
B . . . B 0
The optimal control input is obtained from the so-
lution of the Riccati equation in a similar way,
¯
S
MR
(
¯
kN ) =
¯
Q
MR
−
¯
M
MR
¯
R
−1
MR
¯
M
T
MR
+[
¯
A
T
MR
−
¯
M
T
MR
¯
R
−1
MR
¯
B
T
MR
]
·
¯
S
MR
(
¯
kN +N)·[
¯
A
MR
−
¯
B
T
MR
(
¯
R
−1
MR
¯
M
T
MR
+
¯
K
MR
(
¯
kN ))]
¯
K
MR
(
¯
kN ) = [
¯
R
MR
+
¯
B
T
MR
¯
S
MR
(
¯
kN +N)
¯
B
MR
]
−1
¯
B
T
¯
S
MR
(
¯
kN +N)·
·(
¯
A
MR
−
¯
B
MR
¯
R
−1
MR
¯
M
T
MR
)
¯u(
¯
kN +N) = −(
¯
R
−1
MR
¯
M
T
MR
+
¯
K
MR
(
¯
kN ))·¯x(
¯
kN )
LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS
71

4 MULTI-RATE BUCY-KALMAN
FILTER
The limit case, when N → ∞ with constant frame-
period, both discrete-time Kalman filters converge to
their equivalent continuous-ones. Continuous lifting
technique must be applied to converge MR-LKF into
its equivalent one (Bamieh et al., 1991). In this pa-
per the convergence of MR-PKF to the Bucy-Kalman
filter (continuous) is shown.
The prediction and correction covariance equations
for a sampled-data system is,
P(t+T |t)= e
A
c
T
·P(t|t)·e
A
T
c
T
+ Q(T )
S
s
(t)= C
s
(t)P(t+T |t)C
T
s
(t)+R
s
(T )
K
s
(t+T )= P(t+T |t)·C
T
s
(t)·S
−1
s
(t)
P(t+T |t+T )= P(t+T |t)−K
s
(t+T )·C
s
(t)·P(t + T |t)
being C
s
(t) the output matrix considering the multi-
rate sampling. The derivate of the covariance is,
˙
P(t|t) = lim
T →0
P(t+T |t+T )−P(t|t)
T
˙
P(t|t) = lim
T →0
∂P(t+T |t)
∂T
− lim
T →0
∂K
s
(t+T )
∂T
·C
s
(t)·P(t+T |t)−
− lim
T →0
K
s
(t+T )·C
s
(t)·
∂P(t+T |t)
∂T
Operating and re-ordering some terms,
lim
T→0
∂P(t+T |t)
∂T
=
˜
˙
P(t|t) = A
c
·P(t|t)+P(t|t)·A
T
c
+G
c
·Q
c
·G
T
c
lim
T→0
∂K
s
(t+T )
∂T
C
s
(t)P(t+T |t) =
˜
˙
P(t|t)C
s
(t)K
T
s
(t)−
−K
s
(t)
˙
S
s
(t)K
T
s
(t)
lim
T→0
K
s
(t+T )C
s
(t)
∂P(t+T |t)
∂T
= K
s
(t)C
s
(t)
˜
˙
P(t|t)
where
˙
S
−1
s
(t) = −S
−1
s
(t)
˙
S
s
(t)S
−1
s
(t). Operating, we
get to multi-rate Bucy-Kalman filter equations:
˜
˙
P(t|t)= A
c
·P(t|t)+P(t|t)·A
T
c
+G
c
·Q
c
·G
T
c
K
s
(t)=
˜
˙
P(t|t)C
T
s
(t)
C
s
(t)
˜
˙
P(t|t)C
T
s
(t) + R
s
(t)
−1
˙
P(t|t)=
˜
˙
P(t|t)−K
s
(t)·C
s
(t)·P(t|t)
Finally, the state estimation is as follows:
ˆ
˙x(t)= A
c
·ˆx(t)+B
c
·u
h
(t)+K
s
(t)(y
s
(t)−C
s
(t)·ˆx(t))
5 NUMERICAL EXAMPLE
Suppose the weak-coupled plant proposed by (Araki
and Yamamoto, 1986; Godbout et al., 1990), with in-
puts u
1
and u
2
updated at T
u
1
= 0.1sec. and T
u
2
=
0.15 sec. and outputs y
1
and y
2
sampled at T
y
1
= 0.15
sec. and T
y
2
= 0.1 sec., respectively. The base-period
is T = 0.05 sec. and the frame-period
¯
T = 0.3 sec.,
thus N =6.
˙x(t)= A
c
·x(t)+B
c
·u(t)+w(t)
y(t) =C·x(t)+v(t)
with,
x(t)= [x
1
x
2
x
3
]
T
, u(t)= [u
1
u
2
]
T
, y(t) = [y
1
y
2
]
T
A
c
=diag{−2.5, −2, −1}
B
c
=
2.5 0
10 −1.2
5/6 1
, C =
−4 1 0
−1/3 0 1
where noise covariances are Q
c
=
diag{0.05, 0.3, 0.1} and R
c
=diag{0.1, 0.1}.
The lifted input and output vectors are:
¯u(
¯
kN ) = [u
1
(
¯
kN−N ) u
2
(
¯
kN−N ) u
1
(
¯
kN−4) u
2
(
¯
kN−3) u
1
(
¯
kN−2)]
T
¯y
s
(
¯
kN ) = [y
2
(
¯
kN−4) y
1
(
¯
kN−3) y
2
(
¯
kN−2) y
1
(
¯
kN ) y
2
(
¯
kN )]
T
while the periodic time-variant vectors and matrices
are,
∆
u
(0) = I ∆
u
(1) = 0 ∆
u
(2) = ∆
u
(4) =
1 0
0 0
∆
u
(3) =
0 0
0 1
y
s
(0) = [y
1
y
2
]
T
, y
s
(1) = y
s
(5) = ∅, y
s
(2) = y
s
(4) =y
2
, y
s
(3) = y
1
Figure 2 shows the state covariance computation
using a MR-LKF and MR-PKF for unit step with
ZOH. The MR-LKF is combined with the fast sam-
pling model of the plant (inter-sampling prediction).
It can be observed that the covariance (and also the
estimation error, which is not represented), are the
same at every frame-period, therefore both filters are
equivalent at those time instants. However, the advan-
tage of the multi-rate periodic time-variant approach
is that estimations are performed at a fast sampling
rate, while the lifting approach is in open-loop until
all inputs and output of the frame-period have been
processed.
0 0.5 1 1.5
0
0.05
0.1
+3σ x
1
0 0.5 1 1.5
0
0.1
0.2
+3σ x
2
0 0.5 1 1.5
0
0.1
0.2
Time [sec.]
+3σ x
3
Figure 2: State covariance for MR-LFK (dotted line) and
MR-PKF (dashed line).
Now, can compare the equivalence of the perio-
dic and lifted LQG control using a ZOH. In figure
3, it is depicted the state evolution with initial val-
ues x(0) = [0.5 −0.4 0.3]
T
, and weighting matrices
˜
Q
c
= 10·I
3×3
,
˜
R
c
= 0.1·I
2×2
. It can be appreciated
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
72
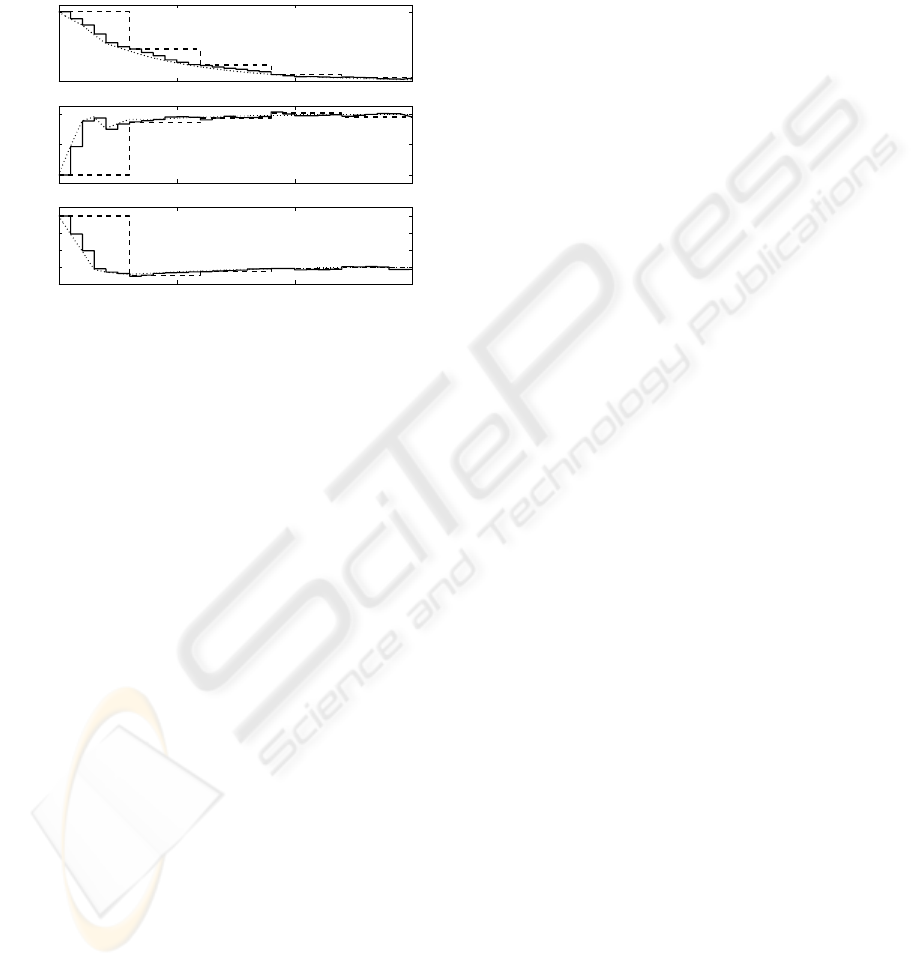
that in both cases, they give the same estimation each
frame-period, however in the periodic approach the
state estimation is much more closer to the real state.
This is because the lifted LQG is in open-loop among
frame-periods. Figure 3 shows the state evolution for
the proposed example, where the same conclusions
can be obtained.
0 0.5 1 1.5
0
0.5
x
1
0 0.5 1 1.5
−0.4
−0.2
0
x
2
0 0.5 1 1.5
−0.1
0
0.1
0.2
0.3
x
3
Time [sec.]
Figure 3: State estimation in LQG control, with the perio-
dic regulator (solid line) with the lifted regulator (dashed
line) and the real state evolution of multi-rate LQR control
(dotted-line).
6 CONCLUSIONS
In this paper, we have presented and formalized two
Linear Quadratic Gaussian regulators for multi-rate
sampled-data systems, using time invariant (lifting
technique) and time variant (periodic) modeling. In
the numerical example, it has been shown that both
approaches are equivalent at frame period, since they
are representing the same sample-data system.
The lifted LQG regulator is expressed with con-
stant coefficient matrices and executed at the frame-
period. This implies a partial open loop control
among frame-periods. On the contrary, the periodic
LQG is executed at base-period and consequently, it
is a time-variant system. In addition, this regulator
is not restricted to periodic sampling and can also be
used for dealing with data-missing problems without
recomputing the system model.
In both regulators, multi-rate holds are integrated
as signal interfaces for different frequencies. Gen-
eral multi-rate holds are based on primitive functions.
In particular, from polynomial functions it is possible
to generate multi-rate ZOH, FOH, etc. Other less-
conventional holds based on non-polynomial func-
tions may improve signal reconstruction and even sys-
tem behavior. The wide variety of holds proposed di-
rectly in this paper or indirectly in other authors’ ref-
erences, open a research field to be exploited.
An interesting analysis has been done to demon-
strate the convergence of the Periodic Kalman filter
to its equivalent continuous one (Bucy Kalman fil-
ter), when the periodicity ratio converges to infinity.
A new approach related with Bucy Kalman filter is
the fact that continuous signals with discontinuities
can be easily incorporated for estimation.
The multi-rate periodic modeling can be also used
in non-linear filters such as Extended and Unscented
Kalman Filters and Particle Filters, widely used in
mobile robotics.
Many technological limitations associated to sen-
sors and actuators can be overtaken in a systematic
way, using the multi-rate sampling approaches used
in this paper.
REFERENCES
Albertos, P. (1990). Block Multirate Input-Output model
for sampled-data control systems. IEEE Trans. on Au-
tomatic Control, AC-35(9):1085–1088.
Araki, M. and Yamamoto, K. (1986). Multivariable mul-
tirate sampled-data systems: State-space description,
transfer characteristics and nyquist criterion. IEEE
Trans. on Automatic Control, AC-31(2):145–154.
Armesto, L., Chroust, S., Vincze, M., and Tornero, J.
(2004). Multi-rate fusion with vision and inertial sen-
sors. In Int. Conf. on Robotics and Automation, pages
193–199.
Armesto, L. and Tornero, J. (2003). Dual-rate high order
holds based on primitive functions. In American Con-
trol Conference, pages 1140–1145.
Armesto, L. and Tornero, J. (2004). Slam based on kalman
filter for multi-rate fusion of laser and encoder mea-
surements. In IEEE Int. Conf. on Intelligent Robots
and Systems, pages 1860–1865.
Bamieh, B., Pearson, J., B.A., F., and A., T. (1991). A lift-
ing technique for linear periodic systems with appli-
cations to sampled-data control. Systems and Control
Letters, 17:79–88.
Braslavsky, J. H., Middleton, R. H., and Freudenberg, J. S.
(1998). L2-induced norms and frequency gains of
sampled-data sensitivity operators. IEEE Trans. on
Automatic Control, 43(2):252–258.
Chen, T. and Francis, B. (1995). Optimal Sampled-data
Control Systems. Springer-Verlag, London.
Colaneri, P. and de Nicolao, G. (1995). Multirate LQG con-
trol of continuous-time stochastic systems. Automat-
ica, 31:591–596.
Godbout, L., Jordan, D., andApostolakis, I. (1990). Closed-
loop model for general multirate digital control sys-
tems. In IEEE Proceedings, volume 137 of D, pages
326–336.
LINEAR QUADRATIC GAUSSIAN REGULATORS FOR MULTI-RATE SAMPLED-DATA STOCHASTIC SYSTEMS
73

Hong, L. (1994). Multirate estimation. In Proceedings
of the IEEE Aerospace and Electronics Conferences,
pages 435–440.
Julier, S. and Uhlmann, J. (2002). Reduced sigma points
filters for the propagation of means and covariances
through nonlinear transformations. In American Con-
trol Conference, volume 2, pages 887–892.
Julier, S., Uhlmann, J., and Durrant-Whyte, H. F. (2000).
A new method for the nonlinear transformations of
means and covariances in filters and estimators. IEEE
Transactions on Automatic Control, AC-45:477–482.
Kabamba, P. (1987). Control of linear systems using gen-
eralized sampled-data hold functions. IEEE Transac-
tions on Automatic Control, pages 772–783.
Khargonekar, P., Poolla, K., and Tannenbaum, A. (1985).
Robust control of linear time-invariant plants using
periodic compensation. IEEE Transactions on Auto-
matic Control, AC-30:1088–1985.
Kranc, G. (1957). Input-output analysis of multirate feed-
back systems. IEEE Transactions on Automatic Con-
trol, AC-3:21–28.
Lee, D. and Tomizuka, M. (2003). Multirate optimal state
estimation with sensor fusion. In American Control
Conference, pages 2887–2892.
Loan, C. V. (1978). Computing integrals involving the
matrix exponential. IEEE Trans. Automatic Control,
23:395–404.
Qui, L. and Chen, T. (1999). Multi-rate sampled-data sys-
tems: All H
∞
suboptimal controllers and the mini-
mum entropy controller. IEEE Trans. Automatic Con-
trol, 44(3):537–550.
Shah, S., Gudi, R., and M.R., G. (1995). Adaptative multi-
rate state and parameter estimation strategies with ap-
plication to a bioreactor. AICHE Journal, 412:2451–
2464.
Tangirala, A., Li, D., Patwardhan, R., Shah, S., and Chen,
T. (1999). Issues in multi-rate process control. In Pro-
ceedings of the American Control Conference, pages
2771–2775.
Tornero, J. (1985). Non-conventional sampled-data systems
modelling. Control System Center Report 640/1985,
University of Manchester (UMIST).
Tornero, J., Albertos P., and Salt J. (1999). Periodic optimal
control of multirate sampled data systems. In 14th
World Congress of IFAC, pages 211–216, China.
Tornero, J. and Armesto, L. (2003). A general formulation
for generating multi-rate models. In American Control
Conference, pages 1146–1151.
Tornero, J. and Tomizuka, M. (2002). Modeling, analysis
and design tools for dual-rate systems. In American
Control Conference, pages 4116–4121.
Zhang, H., Basin, M., and Skliar, M. (2004). Optimal
state estimation with continous, multirate and ran-
domly sampled measurements. In Proceedings of the
American Control Conference.
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
74
