
NEURAL NETWORK BASED DATA FILTERING FOR POSITION
TRACKING OF AN UNDERWATER VEHICLE
M. Ufuk Altunkaya, Serhat İkizoğlu
Electrical Engineering Dept., Istanbul Technical University, Istanbul, Turkey
Fikret Gürgen
Computer Eng. Dept., Boğaziçi University Istanbul, Turkey
Keywords: INS, inertial navigation, piecewise neural networks, acceleration data, filtering, backpropagation, radial
basis, position estimation.
Abstract: As a side effect of the developments in the mobile robotics, navigational technology has gained a leap
recently. Although the most popular navigational aid for trajectory tracking is the Global Positioning
System (GPS), it has also some disadvantages. Therefore attentions are drawn to other navigational devices
such as Inertial Navigation Systems. Taking the underwater implementations of vehicle navigation into
account, INS becomes a necessity due to communicational problems between the GPS and the satellites. On
underwater vehicles Inertial Navigation Systems consisting of Inertial Measurement Units (IMU) such as
accelerometers and gyros are used combined with other navigational devices like GPS or sonar. The error of
the IMU output makes it necessary to be accompanied by an additional device. In this paper a neural
network based filtering system is introduced that is planned to be used for the trajectory tracking of an
underwater vehicle.
1 INTRODUCTION
Today several systems are used for accurate position
tracking of vehicles. Among them the most
commonly used one is the Global Positioning
System (GPS). But even this system is not perfect,
and some additional units are employed to correct
the data given by the GPS. Generally an Inertial
Measurement Unit (IMU) is utilized for this
purpose. The whole system is called an Inertial
Navigation System (INS). Recently there is a trend
to omit the GPS due to its unreliability at certain
situations. As GPS uses satellites, it cannot be used
whenever the connection with the satellites is
corrupted (due to poor satellite geometry, high
electromagnetic interference, high multipath
environments, or obstructed satellite signals). In
addition, the INS system provides much higher
update positioning rates compared with the output
rate conventionally available from GPS (Hiliuta et
al, 2004). Also this system is strategically dangerous
as it is used for military purposes.
2 THE SYSTEM
Our aim in this study is the accurate tracking of an
underwater vehicle which can travel without any
external guidance. Therefore, an IMU (Microstrain
3DM-G) that consists of a 3D-accelerometer, a 3D-
gyroscope and a 3D-magnetometer is chosen for this
purpose. Using this device, the position tracking can
be done by double integrating the acceleration data.
But if there is any noise or bias at the output data of
the accelerometer, then this error will increase with
each integration step. To overcome this problem the
output data must be filtered. There are different
methods used for filtering the sensor data, from
conventional filters to Kalman filtering. This paper
introduces the study of a signal filtering method
depending on neural network methodology. For this
purpose Matlab and Simulink programs are used.
Both the reading process of the acceleration data and
teaching the neural network are done by Matlab
while Simulink is used for the simulation of the
197
Ufuk Altunkaya M., Ä
ˇ
rkizo
˘
glu S. and Gürgen F. (2006).
NEURAL NETWORK BASED DATA FILTERING FOR POSITION TRACKING OF AN UNDERWATER VEHICLE.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 197-200
DOI: 10.5220/0001216901970200
Copyright
c
SciTePress
position tracking for the previously prepared neural
network models.
2.1 Errors of the Inertial Sensors
In the IMU, there are two main sources of error that
occur at the inertial sensors: The sensor bias and the
noise of the sensor data. (Other errors are scale
factor and axes misalignment, (Hou, 2004)).The
bias for accelerometers and gyros is described as the
output value for zero input. The effect of the bias of
an accelerometer on the velocity and position
calculations is:
∫∫
∫
===
==
2
21 tbtdtbvdtpe
tbdtbve
ff
ff
(1)
where
pebve
f
,
stand for velocity error, sensor bias
and position error respectively. Also the effect of the
noise upon the position calculation is similar. Since
ve and pe would increase with time, it is very
important to filter the disturbing signals.
2.2 Filtering Methods
Advanced filtering methods like the Kalman Filter
are mostly preferred for high precision filtering. By
these methods, also called the Stochastic Modeling
Methods, first the error is modeled, and then this
calculated error is filtered. Haiying Hou (2004) has
made a comparison of the Kalman Filter and some
other stochastic modeling methodologies.
Great care must be taken for determining the
coefficients of the Kalman Filter and modeling.
Since in our system the sampling rate is determined
due to the performance of the computer Matlab is
running on, it’s hard to model the system from the
samples taken. On the other hand, as our aim is to
design a system that can be employed in different
environments and on different types of vehicles, we
prefer a model-free concept. Thus, using a neural
network based learning algorithm that can be trained
in the form of the real data would result in a better
filtering.
3 THE STUDY: NEURAL
NETWORK BASED FILTERING
Although neural network based systems are recently
used for trajectory tracking they are mostly
employed in INS-GPS integrated applications
(
Noureldin et al, 2004, Kaygisiz et al, 2003). In these
applications neural networks are trained to follow up
the position of the vehicle and are aimed to converge
to the INS position data in order to trace the route in
the absence of the GPS.
3.1 Algorithm Comparison
In our study we first compared network architectures
using the two main algorithms: The Multi-layer
Perceptron Backpropagation Feed-forward Networks
and the Radial Basis Neural Networks.
In order to compare the algorithms we need a
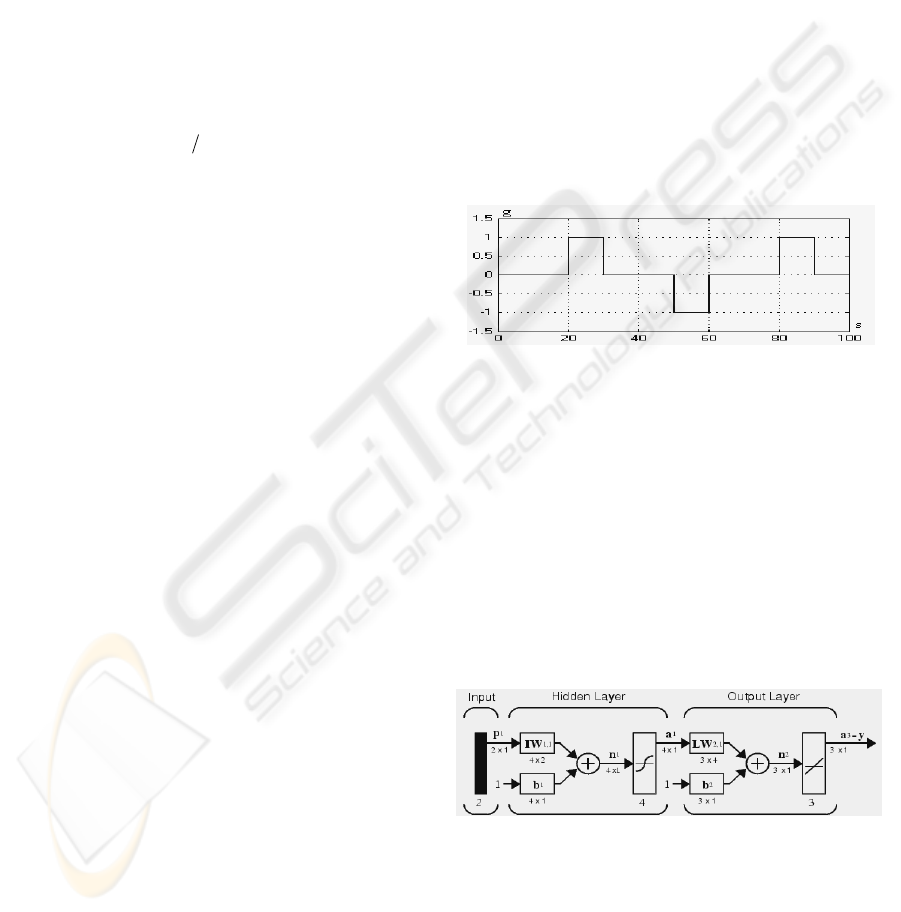
“known” signal and a noisy one. The signal with 1g
amplitude in Figure 1 forms our “known” signal.
The noisy signal is constructed as the superposition
of the known signal and the output data of the sensor
for the steady state that constitutes the noise-data.
Figure 1: The “known” acceleration data.
3.1.1 The Backpropagation Algorithm
The Back-propagation method, sometimes also
called the generalized delta rule, is commonly
applied to feedforward multilayer networks. Here
the weights and the biases are adjusted by error-
derivative (delta) vectors back-propagated through
the network. Figure 2 shows the architecture of a
feedforward neural network using the
backpropagation algorithm with one hidden layer of
sigmoid neurons and an output layer of linear
neurons.
Figure 2: Back-propagation Neural Network Architecture.
In this study following network architectures
using back-propagation algorithms are trained and
compared: Gradient Descent (GD), Gradient
Descent with Momentum Back- Propagation
(GDM), Gradient Descent with Adaptive Learning
Rate Back Propagation (GDX) and Levenberg-
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
198
Marquardt Back Propagation (LM). Among these
Levenberg-Marquardt methodology has given the
best result (Figure 3).
Figure 3: Training with Levenberg-Marquardt Algorithm.
3.1.2 The Radial Basis Neural Network
The Radial Basis Function is a curve fitting method
applied in multi-dimensional space. A radial basis
neuron acts as a detector that produces 1 whenever
the input p is identical to its weight vector w. The
bias b allows the sensitivity of the neuron in the
radial basis layer to be adjusted (Figure 4).
Figure 4: Radial Basis Neural Network Algorithm.
For comparison, Radial Basis Network (RB),
Exact Radial Basis Network (RBE) and
Generalized
Regression Neural Network (GRNN) architectures
are trained. Due to the comparison the Generalized
Regression Neural Network has given the best
convergence as shown at Figure 5.
Figure 5: Training with Generalized Regression
Algorithm.
3.1.3 Back-Propagation vs. Radial Basis
Neural Network
The two best trained architectures using different
algorithms are compared within the Matlab/Simulink
model of the system.
The position data obtained by double integrating
the “known” acceleration data is given in Figure 6:
Figure 6: The true position data.
Comparing the two networks denotes that
filtering with the backpropagation neural network
(lighter line) ends up with an error of about 5m more
than the one using the radial basis network (darker
line) over a 4000m distance (Figure 7).
Figure 7: Errors of the radial basis and the back-
propagation network outputs for position data.
Although they may require more neurons
comparatively, the Radial Basis Networks can be
trained in a much shorter time than the standard
feedforward networks. Therefore we have chosen
Radial Basis Neural Network architecture as the
optimum network for our study.
3.2 Methods to Obtain Accurate
Position Tracking Using Neural
Network Based Optimisation
After choosing the optimum neural network
algorithm, we designed different filtering
architectures to get the best position estimation using
the acceleration data of the vehicle.
Whilst filtering the noise on the acceleration
output, the true data also deforms causing an error
which increases with each integration. Therefore, we
decided to compare the results for filtering the
velocity and position data respectively.
3.2.1 Velocity-Data Filtering
After filtering the noisy velocity data, position
estimation is obtained by integrating the velocity
data once. The errors of the filtered and the noisy
data are given in Figure 8, the darker line
representing the filter output.
NEURAL NETWORK BASED DATA FILTERING FOR POSITION TRACKING OF AN UNDERWATER VEHICLE
199
Figure 8: Position errors of the integrated noisy and filtered
velocity data.
3.2.2 Position-Data Filtering
The errors given in Figure 9 belong to the noisy
position data obtained by double integrating the
noisy acceleration data, and the filtered noisy data.
(The dark line represents the filtered signal.)
Figure 9: Errors of the noisy and filtered position data.
The comparison of the three filtering processes
applied for different versions of the data leads to the
conclusion that filtering the acceleration data gives
the best result (Fig. 10). The closest (light) line to
the horizontal axis at zero value represents the
output of acceleration filtering. The data with
positive hunch values correspond to the output of
position filtering and the third curve describes the
output of velocity filtering.
Figure 10: Comparison of position data obtained from
acceleration, velocity and position filtering.
3.2.3 Filtering with Piecewise Trained
Networks
Constructing a system composed of neural networks
each of which is trained for a special situation can
provide dynamic position estimation.
A switching model, containing neural networks
trained for different phases of input as zero input,
increasing / decreasing input and non-zero constant
value input is designed. The system uses the specific
neural network to filter for the specific part of the
data whenever the system detects the input in any of
these forms. Thus the system can adapt to different
trajectories of the vehicle.
The system tested with the “known”
acceleration data (Figure 1) is observed to filter the
noise with a high accuracy as seen in Figure 11.
Figure 11: Position errors of the Piecewise Neural
Network (darker line) and the noisy data.
4 CONCLUSION
In this study neural network based filtering models
are tested using data sets constructed from the
readouts of an IMU and user-defined signals in order
to simulate the trajectory of an underwater vehicle
with good estimations of position data. As the
piecewise neural network filter offers the best
performance among all and also gives satisfactory
results, we have decided to use this method for our
further practical studies.
REFERENCES
Hiliuta, A., Landry, R. JR., Gagnon, F., 2004. Fuzzy
Corrections in a GPS-INS Hybrid Navigation System.
In IEEE Transactions on Aerospace and Elecronic
Systems Vol. 40, No.2.
Hou, Haiying (2004) Modeling Inertial Sensors Errors
Using Allan Variance, Department of Geomatics
Engineering, The University of Calgary, Calgary,
Canada.
Kaygisiz, B.H.; Erkmen, A.M.; Erkmen, I. 2003 GPS/INS
Enhancement Using Neural Networks For
Autonomous Ground Vehicle Applications. Intelligent
Robots and Systems, (IROS 2003)
Noureldin, Aboelmagd; Osman, Ahmed, El-Sheimy,
Naser 2004 A Neuro-Wavelet Method For Multi-
sensor System Integration For Vehicular Navigation.
Journal of Measurement Science and Technology,
Volume 15, Issue 2, pages 404-412.
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
200
