Blind Source Separation Based on a Single Observation

Damjan Zazula, Aleš Holobar

University of Maribor, Faculty of EE and CS

Smetanova 17, 2000 Maribor, Slovenia

Abstract. This paper deals with a novel approach to the compound signal

decomposition. It takes adv

antage of blind source separation using the

algorithm for convolution kernel compensation (CKC). We derive a version

which cope with compound signals, mixtures of several source contributions,

even if only a single observation is available. Our novel approach detects and

separates the triggering instants of all source symbols which contribute to the

processed observation. The obtained decomposition is very robust and accurate.

We experimented with synthetic signals having characteristics similar to the

electrocardiographic (ECG) signals. Also at signal-to-noise ratios (SNRs) as

low as 0 dB, the obtained average true positive statistics for the detected source-

symbol triggerings was 98±1%, average false positive statistics 2±1%, and false

negative statistics 3±2%.

1 Introduction

Many natural and technological phenomena can be modelled as multiple-input

multiple-output (MIMO) systems. Observing compound signals, for example, such as

telecommunication, bioelectrical, seismic, speech or imaging data, successful

approaches are sought to perform a thorough decomposition to the signals’ constituent

components. These components observed, i.e. measured, at multiple system outputs

carry simultaneous information on each system input excitation, which is said to come

from a source, and on the response of the transmission path between a source and an

observation point, i.e., a system channel [1, 2].

On the other hand, any compound signal can be interpreted as a superimposition of

gnal components, which correspond to the individual source symbols generated by

the MIMO input sources. These components, therefore, appear at time instants which

coincide with the triggering (generating) instants of the sources. If the symbol

alphabet is finite, so is the number of different observed signal components. By

reformulating the model in such a way that it describes the observed signal

components and their triggering instants, the characteristics of source symbols and the

model transfer channels are not seen separately any more [1]. There are several

benefits out of this assumption. The first of them brings unification to the

interpretation of all compound signals, regardless their original sources. Secondly,

decomposition of those signals can be focused on the component triggering instants,

which greatly improves its accuracy, robustness, and reliability. So, the

Zazula D. and Holobar A. (2006).

Blind Source Separation Based on a Single Observation.

In Proceedings of the 2nd International Workshop on Biosignal Processing and Classiﬁcation, pages 76-85

DOI: 10.5220/0001224100760085

 SciTePress

decomposition result is a train of triggering pulses. And finally, the observed

individual signal components may be extracted from the observations by different

approaches, such as spike-triggering averaging [11].

Typical observations of compound signals in practice are related to

communications, bioelectrical signals, range imaging, etc. If the input source symbols

can be considered spatially and temporally uncorrelated, a variety of blind source

separation (BSS) techniques serve the decomposition purpose accordingly [3, 4, 5, 6,

7, 8]. When the sources tend to become correlated, more reliable solutions may be

expected using higher-order statistics (HOS) [9, 10], which are also very noise-

resistant. While the BSS methods cope with nonstationary signals, HOS approaches

cannot. On the other hand, the number of observations must exceed the number of

sources to warranty a reliable BSS operation, whereas for HOS there is no such

limitation [10, 11].

Recently, a novel BSS-based method has been proposed. It makes use of the

Mahalanobius distance and angle calculation which, consequently, can lead to the

entire model convolution kernel compensation (CKC). As a result, the system output

observations are blindly deprived of the transfer channel influence and only the

source-symbol triggering pulse trains are extracted [11, 12]. It has been shown that

the source symbols correlated up to 10 % and the underdetermined cases with the

number of observations being as low as a half of the number of source symbols do not

hinder a proper CKC-based decomposition [12].

This paper proposes a novel solution which combines the benefits of the CKC and

HOS approaches. It can cope with an arbitrary underdetermined case in such a way

that it generates additional observations out of the given ones. This generation must

be based on nonlinear operations on the given observations–the linear ones wouldn’t

increase the rank of the CKC decomposition matrix. To demonstrate the idea in an

extreme situation, we are going to deal with only a single observation here, so the

anticipated model will be reduced to a multiple-input single-output (MISO). Adequate

data model and the CKC-based decomposition are presented in Section 2. Section 3

introduces the idea of how to generate more observations out of a single one, while

Section 4 explains this new concept with a short example. The influence of noise and

correlated sources is discussed in the concluding Section 5.

2 Data Model

Recapitulate briefly the reconstruction of source-symbol pulse trains using the CKC-

based decomposition [11, 12]. Consider the following data model:

∑∑

−

=+−=

ijiji

Minvkntkcnx

,,1);()()()( …

(1)

where x

(n) stands for the i-th observation, c

(k) corresponds to the contribution of

length L of the j-th source symbol in the i-th observation, and t

(n-k) denotes a

sequence of triggering instants for this symbol, , with unit-

sample pulses placed at T

∑

∞

−∞=

−=

lTnnt ))(()(

(l) lags, while v

(n) is considered i.i.d. white noise

independent from the sources.

It has been shown [3] that Eq. (1) can be transformed into a multiplicative vector

form as follows:

1,,0);()()(

−

=+= Nnnnn

eeee

…vtCx

(2)

where subscript e designates extended vectors and matrices, C

contains the observed

contributions of source symbols:

⎥

⎦

⎤

⎢

⎣

⎡

MKM







111

(3)

with

⎥

⎦

⎤

⎢

⎣

⎡

−

)1()0(0

0)1()0(

Lcc

ijij







, (4)

(n) stands for the vector of observations, and t

(n) for the vector of triggering

pulses, both at lag n:

eKKee

eMMee

MLntntMLntntn

MnynyMnynyn

)]2(),....,(),....,2(),....,([)(

)]1(),....,(),....,1(),....,([)(

+−−+−−=

+−+−=

(5)

Extended noise vector v

(n) is considered constructed in the same way. M

in Eqs.

(5) means an extension factor. If it fulfils the following inequality

)1( −+≥⋅

MLKMM

, (6)

then for K different source symbols of length L and M observations the matrix C

is of

full column rank. This condition warranties a successful elimination of contributions

of C

, as we are going to show in the next section.

2.1 Convolution Kernel Compensation

Recall Eq. (2). It has a typical MIMO structure. From this point of view, Ce is a

convolution kernel convolving t

(n) into the observations x

(n). Given x

, if we can

get rid of C

the triggering instants of unknown source symbols, t

, would be

obtained. We called this process “convolution kernel compensation (CKC)”.

Observe the following expression:

)()(

xRx

−

(7)

where stands for the sample correlation matrix:

ICRCICttCxxR

σσ

+=+==

eee

(8)

with denoting sample correlation matrix of source triggering trains of pulses,

and the expression σ

I represents the noise, v

, correlation matrix.

For easier comprehension of derivation, continue with the noise-free case. By

substituting (8) into (7), we see that convolution kernel is eliminated:

)()()()()()(

1111

nnnnnn

eeee

eee

tRttCCRCCtxRx

ttx

−−−−−

(9)

The expression from (7) is known as Mahalanobius distance, which, as it is clear

from Eq. (9), yields only the information on source triggering instants. Actually, its

value depends on the number of sources active in given time instant n. This is why we

call it activity index.

Suppose we deal with orthogonal sources and n

indicates the time instant where

one of them generates a symbol (its contribution appears in the observation). Then

vector t

) is all zero except the element which belongs to the generated symbol, say

the i-th, and equals 1. Besides, matrix is diagonal, and so is . It is then

straightforward that

1−

)()()()()()()()(

,,,0,,

ntrntntrnnnnnp

ieiiieieiie

ein

====

−−

tRtxRx

(10)

where r

i,I

denotes the i-th diagonal element of , and t

1−

e,i

(n) stands for the train

value at lag n for the i-th source symbol. Evidently, taking all possible n’s into

account, Eq. (10) produces a sequence

in ,

whose values equal the i-th source-

symbol triggering pulse train to a constant amplitude factor, r

i,i

. So, all repetitions of

that symbol are detected.

The values of activity index indicate those lags n

where individual sources

contribute their symbols. If we select such n

’s that cover all different source contribu-

tions, a thorough decomposition is done and all source-symbol triggering pulse trains,

; i∈[1,K], are separated.

Once the triggering instants of the signal components, i.e. the source-symbol pulse

trains, are known, also the components themselves can be obtained–for example, by

using the spike-triggered averaging throughout the given observations.

3 An Upgrade of the CKC-based Decomposition Using a Single

Observation

Suppose the data model from Eq. (1) represents a MISO instead of a MIMO system–

so, only a single observation x

(n); n=0,…,N-1, is available. The necessary condition

(6) for a thorough decomposition can, therefore, not be met.

Now, try to increase the number of observations artificially as follows. Assuming

every observed sample x

(n) an independent random variable, new observations may

be generated using higher-order moments of these variables. Also cross-moments may

be applied by combining the variables at different observation lags. In the

continuation, we will talk only the moments at a given lag, actually meaning the dot-

operations (according to MATLAB) with the given shift of the observation

repetitions. This will give additional, artificial observations; however, it will also

produce additional, artificial source symbols. For instance, taking the second-order,

zero-lag moments, all the observation samples that comprise superimpositions of

several source activities will generate new artificial sources whose activity is

determined by pair-wise logical products of the superimposed source activities. Such

artificially introduced source symbols will be called cross-symbols, s

(n), if i and j are

two intersecting, superimposed sources in the observation sample n, s

(n)=s

(n)·s

(n-

), where d

is a time shift between the triggerings of sources i and j.

Any zero-lag higher-order moment can generate one additional (artificial)

observation. How about the nonzero lags? Suppose source triggers with a minimum

distance of T

min

between the adjacent symbols. Suppose also those source symbols

contribute signal components whose length in observation equals L, L<T

min

. It is

necessary, then, to limit the lags respected in higher-order moments to Λ=T

min

-L. This

assumption is correct with all possible applications mentioned in Section 1.

Remember we have only a single observation available, x

. Hence, all additional,

artificial observations will be derived from it. Denote them by y and a set of indexes:

the number of indexes is going to be equal to the order of moments applied, and the

values of indexes are going to define the shifts among the combined observation

repetitions. Make this more comprehensible by a short example; let

[]

65432101

,,,,,,)( aaaaaaanx =

be an observation which can be further designated as

{}

)()(

nxny

Second-order moments at zero lag will be calculated as:

{}

[

]

00,0

,,,,,,)( aaaaaaany =

giving the first artificial observation whose sample values equal the squares of the

values in x

. Further non-zero lags are possible, such as:

{}

[

]

0,,,,,,)(

6554433221101,0

aaaaaaaaaaaany =

with the second repetition of x

shifted anticausally by one sample. Also y

{0,-1}

(n) is

feasible, but because y

{0,-1}

(n)= y

{0,1}

(n) no new observation is obtained.

We have already mentioned that added artificial observations introduce new source

symbols as well. Actually, they contribute new signal components which consist of

non-linear combinations of the responses to the original source symbols. Whenever a

superimposition of two or more source contributions appear in an observation sample,

the artificial observations based on higher-order moments need also additional,

artificial sources to be modelled by MIMO. Exemplify this statement by a concrete

situation. Suppose we have two components, c

(n)=[a

] and c

(n)=[b

superimposed in our observation, so that:

(n)=[a

,0,a

,0,b

]

It is obvious that c

(n) appears alone first, then at location 4 it overlaps with c

(n-

1), while at location 9 c

(n) appears alone. Using the triggering train of pulses, t, a

matrix form follows:

[]

tC ⋅=

⎥

⎦

⎤

⎢

⎣

⎡

1,0,0,0,1,0,0,0,0,0,0,0

0,1,0,0,0,1,0,0,0,0,0,0

0,0,1,0,0,0,1,0,0,0,0,0

0,0,0,0,0,1,0,0

,0,1,0,0

0,0,0,0,0,0,1,0,0,0,1,0

0,0,0,0,0,0,0,1,0,0,0,1

,,,,,)(

3213211

bbbaaanx

Let us now construct the artificial observation with second-order moments at zero

lag:

{}

],,,0,,2,2,,0,,,[)(

223

112

10,0

bbbbbbaabbaaaaaany ++++=

The original observation and the added artificial one can be described by a unified

matrix form:

{}

tC ⋅=

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

0,0,0,0,0,1,0,0,0,0,0,0

0,0,0,0,0,0,1,0,0,0,0,0

1,0,0,0,1,0,0,0,0,

0,0,0

0,1,0,0,0,1,0,0,0,0,0,0

0,0,1,0,0,0,1,0,0,0,0,0

0,0,0,0,0,1,0,0,0,1,0,0

0,0,0,0,0,0,1,0,0,0,1,0

0,0,0,0,0,0,0,1,0,0,0,1

2,2,,,,,,

0,0,,,,,,

)(

2312

321321

0,0

bababbbaaa

bbbaaa

(11)

Both the convolution kernel C and the triggering pulse trains change by adding

artificial observations. From Eq. (11), it is clear how new sources are artificially

introduced and what is their role (see the two bottom rows in t).

Eq. (11) also explains the most important contribution of added artificial

observations: the rank of convolution kernel C increases. When dealing with finite

alphabet of source symbols, e.g. K, it can be shown that with adequate number of

artificial observations the convolution kernel matrix C obtains full column rank. This

leads to a signal decomposition which is Bayesian optimal, as defined in the

preceding section [13].

The only problem of this kind of approach is that the decomposed source-symbol

triggering trains split among several artificial sources. Whenever there are

superimpositions of source-symbol contributions within an observation, every type of

superimposition is decomposed to its own triggering pulse train. Consequently, the

triggerings which appear in those trains disappear from the trains of the sources

whose symbol contributions overlap.

There are practical cases where this effect is not disturbing. This certainly is true for

the observations with non-overlapping contributions, such as electrocardiograms

(ECG) or, partially, images. We are going to elaborate our approach with non-

overlapping assumption in the next section.

4 Simulation Results

To exemplify the derivation from Section 3, we decided to simulate an artificial

observation with characteristics similar to the ECG signals. We synthesised the

following:

four random generated source contributions with lengths L = 8, 10, 5 and 7

samples, respectively;

2. random appearance of these source contributions in the generated observation,

so that their intermediate mean distances were 50, 1000, 500, and 3000

samples, respectively, while actual appearances were Gaussian distributed

around these values with standard deviation of 2 samples;

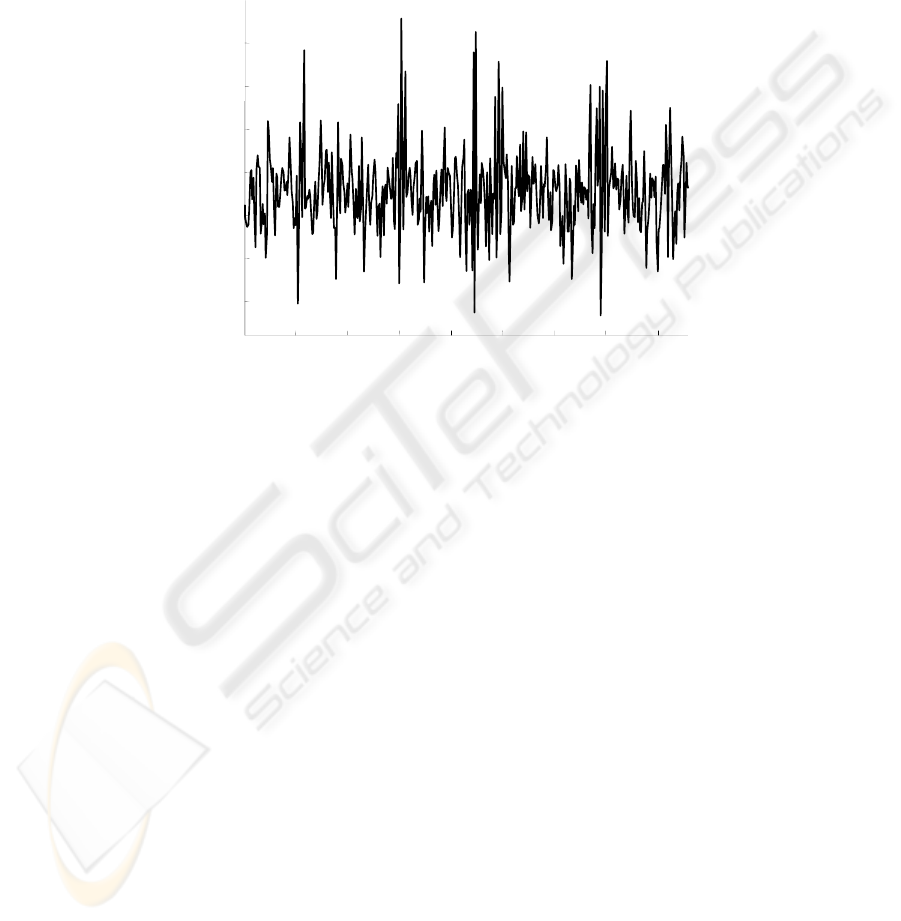
3. the generated observation with length of 10000 samples;

4. artificial observations up to the power of p=3 and shift Λ=4 (according to the

assumptions in Section 3).

Thus, the simulated observation contains four different source contributions. The

one belonging to the first source is most frequent and could be understood as normal

systoles. The other three could be interpreted as different abnormal heart beats, i.e.

extrasystoles and possible pathological changes.

1550 1600 1650 1700 1750 1800 1850 1900

-0.5

-0.4

-0.3

-0.2

-0.1

0.0

0.1

Samples

Amplitude [arbitrary units]

1550 1600 1650 1700 1750 1800 1850 1900

-0.5

-0.4

-0.3

-0.2

-0.1

0.0

0.1

Samples

Amplitude [arbitrary units]

Fig. 1. The generated synthetic observation contaminated with 0 dB additive zero-mean

Gaussian noise. Only a part of the generated signals is depicted.

The total number of artificial observations was 20. We set the number of extended

observations to M

=2 (Eq. (6)). Using our CKC approach [11, 12], we verified the

accuracy of the decomposed triggering pulse trains for the four simulated sources.

Simulations were performed in 10 Monte Carlo runs with different levels of additive

Gaussian noise, so that the SNRs were 20, 15, 10, 5, and 0 dB. An example of the

processed observation with 0 dB additive Gaussian noise is depicted in Fig. 1. Fig. 2

illustrates the decomposition results in the form of the detected triggering pulse trains

for the first source. Trains in black were decomposed at different SNRs, as indicated.

The bottom train of Fig. 2 (in grey) is the original triggering pulse train for the first

source.

200 400 600 800 1000 1200 1400

Samples

SNR [dB]

200 400 600 800 1000 1200 1400

Samples

SNR [dB]

Fig. 2. Reconstructed triggering pulse sequences of source 1 at different SNRs (black) and

original simulated pulses (grey at the bottom). Only a part of the reconstructed pulse sequences

is depicted.

A more detailed analysis of the obtained results versus different SNRs is given in

Tables 1, 2, and 3. Table 1 describes percentages of correctly detected triggering

instants for all four sources (true positive statistics). A triggering instant was

considered correctly detected when the decomposition returned the exact position of

an original source triggering. Tables 2 and 3 collect percentages of false positive and

false negative statistics, respectively.

Table 1. Percentage (mean ± standard deviation) of accurately recognized triggering pulses

(true positive statistics) versus SNR.

SNR 20 dB 15 dB 10 dB 5 dB 0 dB

Source 1

1.00±0.00 0.98±0.02 0.98±0.02 0.99±0.01 0.98±0.01

Source 2

1.00 ± 0.00 0.96 ± 0.01 1.00 ± 0.00 1.00 ± 0.00 0.97 ± 0.01

Source 3

0.99 ± 0.02 1.00± 0.00 0.99 ± 0.02 0.99 ± 0.02 1.00 ± 0.00

Source 4

1.00 ± 0.00 1.00 ± 0.00 1.00 ± 0.00 1.00 ± 0.00 1.00 ± 0.00

Table 2. Percentage (mean ± std) of misplaced pulses (false positive statistics) versus SNR.

SNR 20 dB 15 dB 10 dB 5 dB 0 dB

Source 1

0.00± 0.00 0.02 ± 0.02 0.02 ± 0.02 0.01± 0.01 0.02 ± 0.01

Source 2

0.00± 0.00 0.04 ± 0.01 0.00 ± 0.00 0.00 ± 0.00 0.03 ± 0.01

Source 3

0.01± 0.02 0.00± 0.00 0.01 ± 0.02 0.01 ± 0.02 0.00 ± 0.00

Source 4

0.00± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00

Table 3. Percentage (mean ± std) of missed pulses (false negative statistics) versus SNR.

SNR 20 dB 15 dB 10 dB 5 dB 0 dB

Source 1

0.01± 0.01 0.04 ± 0.01 0.04 ± 0.02 0.03 ± 0.01 0.04 ± 0.02

Source 2

0.01 ± 0.01 0.04 ± 0.03 0.03 ± 0.03 0.03 ± 0.02 0.03 ± 0.01

Source 3

0.01 ± 0.02 0.01 ± 0.02 0.02 ± 0.03 0.03 ± 0.04 0.02 ± 0.03

Source 4

0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00 0.00 ± 0.00

It is obvious that our method is very robust. The worst percentage of the recognised

source triggering instants for the first source is 98%, for the second source 96%, for

the third source 99%, and for the fourth source 100%. As we can see from the tables,

even an extremely high noise with SNR=0 dB does not decrease the successful rate of

the recognised triggering pulses, regardless the triggering frequency as well.

5 Discussion and Conclusions

We have derived an approach which makes a MIMO system decomposition possible

based only on a single observation. It is applicable in the cases with orthogonal, or at

least close-to-orthogonal, sources whose inter-triggering distance is lower bounded.

As already mentioned, an obvious application is ECG signals. The systoles cannot

overlap, and there is always an inter-systole gab which warranties that also the

extended observations would not cause severe overlappings. Referring to the original

MIMO decomposition from [11, 12], two important differences must be reported

here:

1. Nonlinear procedures for generation of artificial observations influence additive

noise which is presumed zero-mean and, thus, prone to elimination by averaging of

the signal samples. Consequently, the observations obtained with the even powers

contain additive noise which is not zero-mean any more. This effect decreases the

algorithm’s robustness.

2. In the MIMO decomposition from [11, 12], it is enough to locate a firing of a

single source, say n

, and x

) can readily be used to extract the complete pulse train

for the source symbol in question (Eq. (10)). The statement equally holds for all

sources in the newly proposed approach described in this paper, so for the cross-

symbols as well. This means that the firing positions of a source symbol will not be

detected when using x

), if n

is a time instant where this source symbol overlaps

with any of other symbols. To detect a single source symbol’s triggering instants, it is

important to find such n

where this symbol appears alone. On the contrary, each point

of a multiple source activity would be recognised as a firing of that artificial source

which was generated by the overlapped multiple source symbols.

To cope with the two problems, special noise-reduction techniques must be

implemented and additional post-processing stages are needed to fuse the detected

pulse trains which belong to the same original source symbol. Both needs further

investigation and explanation which goes beyond the scope of this paper.

Our simulation confirmed that even from a single observation and in very noisy

environment a reliable separation of several sources is feasible using the CKC

approach. Source-symbol triggering instants can be recognised in more then 98% of

cases even when SNR goes as low as 0 dB. This is a very important conclusion for

some practical implementations. Analysing ECG signals, for example, a low number

of observations, if not only a single observation, is available. Nevertheless, the

proposed approach improves significantly the chances of different types of abnormal

heart beats to be recognised and separated from the normal systoles, while for all the

beats their fiducial points can be determined with high precision.

Acknowledgements

This work was partially supported by the NEW project within the European 5

Framework Programme, and partially by the Slovenian Research Programme Funding

Scheme P2-0041.

References

1. Zazula, D., Korže, D., Šoštarič, A., Korošec, D.: Study of Methods for Decomposition of

Superimposed Signals with Application to Electromyograms. In: Pedotti et al. (eds.):

Neuroprosthetics, Springer Verlag, Berlin (1996).

2. Prakriya, S.: Eigenanalysis-based blind methods for identification, equalization, and

inversion of linear time-invariant channels. IEEE Transactions on Signal Processing, Vol.

50, 7 (2002) 1525-1532.

3. Cardoso, J. F.: Blind signal separation: statistical principles. Proceeding of the IEEE.

Special issue on blind identification and estimation, Vol. 9, 10 (1998) 2009-2025.

4. Tong, L., Liu, R.: Blind estimation of correlated source signals. In: Proc. Asilomar Conf.

(1990) 161-164.

5. Belouchrani, A., Meraim, K. A., Cardoso, J. F., Moulines, E.: A blind source separation

technique based on second order statistics. IEEE Transactions on signal processing, Vol.

45, 2 (1997) 434-44.

6. Pham, D. T., Cardoso, J. F.: Blind separation of instantaneous mixtures of non stationary

sources. IEEE Transactions on Signal Processing, Vol. 49, 9 (2001) 1837-1848.

7. Belouchrani, A., Moeness, A. G.: Blind source separation based on time-frequency signal

representation. IEEE Transactions on Signal Processing, Vol. 46, 11 (1998).

8. Holobar, A., Fevotte, C., Doncarli, C., Zazula, D.: Single autoterms selection for blind

source separation in time-frequency plane. In: XI European Signal Processing Conference

EUSIPCO 2002, Toulouse, France (2002) 4 pp.

9. Nikias, C. L., Petropolu, A. P.: Higher-Order Spectra Analysis: A Nonlinear Signal

Processing Framework. Prentice Hall signal processing series, Englewood Cliffs (1993).

10. Zazula, D., Karlsson, S., Doncarli, C.: Advanced signal processing techniques. In R.

Merletti, P. Parker (eds.), Electromyography: physiology, engineering, and noninvasive

applications. John Wiley & Sons, Hoboken, NJ (2004) 259-304.

11. Holobar, A., Zazula, D.: Correlation-based decomposition of surface electromyograms at

low contraction forces. Med. biol. eng. comput., Vol. 42, 4 (2004) 487-495.

12. Holobar, A., Zazula, D.: Correlation-based approach to multichannel blind deconvolution

of binary sources. Submitted to IEEE Trans. on Sig. Proc.

13. Kay, S. M.: Fundamentals of Statistical Signal Processing. Prentice-Hall International,

London (1993).