DETECTION THRESHOLDING USING MUTUAL INFORMATION

Ciar

O Conaire, Noel O’Connor, Eddie Cooke, Alan Smeaton

Centre for Digital Video Processing

Adaptive Information Cluster

Dublin City University, Ireland

Keywords:

thresholding, mutual-information, fusion, multi-modal.

Abstract:

In this paper, we introduce a novel non-parametric thresholding method that we term Mutual-Information

Thresholding. In our approach, we choose the two detection thresholds for two input signals such that the

mutual information between the thresholded signals is maximised. Two efﬁcient algorithms implementing our

idea are presented: one using dynamic programming to fully explore the quantised search space and the other

method using the Simplex algorithm to perform gradient ascent to signiﬁcantly speed up the search, under the

assumption of surface convexity. We demonstrate the effectiveness of our approach in foreground detection

(using multi-modal data) and as a component in a person detection system.

1 INTRODUCTION

The selection of thresholds is an important task in

computer vision and detection systems. A threshold

set too high will result in many missed detections; set

too low, there will be many false positives. A ﬁxed

threshold may not perform well if the properties of the

scene or environment change. For example, the same

threshold is unlikely to be optimised for both daytime

and night time scenes. By dynamically adapting the

threshold to cater for different scenarios, these limita-

tions can be addressed.

Research on dynamic (or adaptive) thresholding

is extensive. The most common approach is to ob-

serve the signal’s properties and to determine the best

threshold to suit these properties. Signal histogram

based methods have generated much interest (Otsu,

1979) (Kapur et al., 1985) (Rosin, 2001). The spatial

distribution of the signal and noise has also been used

(Rosin, 1998). Another similar approach is to per-

form a clustering of signal values, for example, using

K-means (Duda et al., 2001), and to choose a thresh-

old to separate some of the clusters. Our approach is

different in that we do not observe the properties of a

single signal, but observe how the choice of threshold

will affect its relationship with another signal.

Mutual information has been used in computer vi-

sion and machine learning for various applications,

including data alignment (Viola, 1995), particularly

in medical imaging (Pluim et al., 2003). The fusion

of object detector outputs (Kruppa and Schiele, 2001)

and feature selection for classiﬁer training (Peng

et al., 2005) are also applications where mutual in-

formation has proven useful.

In this paper, we introduce a novel non-

parametric thresholding method that we term Mutual-

Information Thresholding. In our approach, the two

detection thresholds for two input signals are selected

so that the mutual information between the thresh-

olded signals is maximised. This encourages high

agreement between detectors, as well as high infor-

mation content. We describe two efﬁcient implemen-

tations of this approach: one using dynamic program-

ming to perform a full-search on the threshold-pair-

space, and another more efﬁcient approach using the

Simplex (Nelder and Mead, 1965) gradient ascent to

ﬁnd the optimum solution, with the assumption of sur-

face convexity.

The paper is organised as follows. We introduce

our thresholding algorithm in section 2 and provide

two efﬁcient implementations in section 3. Section

4 shows the results of using our approach for fore-

ground detection in multi-modal video sequences and

on pedestrian detection in thermal infrared images.

We conclude in section 5 with a summary of the paper

and note some potential areas for future research.

408

Ó Conaire C., O’Connor N., Cooke E. and Smeaton A. (2006).

DETECTION THRESHOLDING USING MUTUAL INFORMATION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 408-415

DOI: 10.5220/0001368404080415

 SciTePress

2 PROPOSED ALGORITHM

There are generally two ways in which different data

sources are combined. One approach is to create a

new data representation, providing a better platform

from which to perform analysis. Examples of this in-

clude linear combinations of the data, fusion using the

max or min operator, or other non-linear combina-

tions. The other common approach is that the analysis

(such as thresholding) is performed separately on both

sources of data and results are subsequently combined

(using a binary operator, such as AND or OR, for ex-

ample). Our novel method is to perform the analysis

on both sources of data simultaneously and to use in-

formation from each source to assist the analysis of

the other. In this way, we obtain results from two sep-

arate sources, but enhanced by each other. We thresh-

old two signals, choosing the thresholds so that the

mutual information between the two thresholded sig-

nals is maximised.

Formally, we describe our algorithm as follows.

We deﬁne a detection score as a conﬁdence mea-

sure that indicates the presence or absence of an

event when it has a high or low value respectively.

Given two sets of detection scores, X and Y , with

X = {x

, ..., x

} and Y = {y

, ..., y

}, that

are aligned (spatially and temporally), we can choose

thresholds, T

and T

, to decide whether the event

was present at a particular point, according to each

set. By thresholding each set, we obtain the event de-

tection sets, X



and Y



, with X



= {x



, ..., x



}

and Y



= {y



, ..., y



1 if x

≥ T

0 otherwise

(1)



1 if y

≥ T

0 otherwise

(2)

These thresholds, T

and T

, are chosen so as to

maximise the mutual information between the distri-

butions of X



and Y



, expressed as

I(X; Y )=



u∈{0,1}



v∈{0,1}

(u, v)log

(u, v)

(u)p

(v)

(3)

where p

(u, v) is the probability that x



= u and



= v, p

(u) is probability that x



= u and p

(v)

is the probability that y



= v. In most applications,

these probabilities are easily computed by counting

occurances and dividing by N.

Choosing the thresholds in this way leads to two

desirable beneﬁts. Firstly, it encourages agreement

between the two detection sets, so that they often

agree on whether the event has been detected or not.

Secondly, it leads to high information content (or

entropy). Without this constraint, agreement could

be maximised by setting the thresholds very high

(or very low) but the detectors would always re-

turn the same answer, regardless of the data they are

analysing.

2.1 Fusion

After thresholding, one is left with two binary maps.

If a single map is required, these results need to be

fused in some way to obtain the ﬁnal decision for

each event. One method is to use a binary operator,

such as AND or OR, to combine the maps. An ap-

proach which is more robust against noise is to use

the spatial information to determine the local support

of each event. Support can be deﬁned, for example, as

the number of neighbouring events that have the same

value as the central event. If the maps disagree on a

detection result, the result with the greater support can

be used. This is very effective at removing isolated

noise. If the support values are equal, this could be

an example of an object which is undetectable in one

modality, such as a room-temperature bag using ther-

mal infrared. Depending on the application, this dis-

agreement could provide additional semantic knowl-

edge.

3 EFFICIENT

IMPLEMENTATION

Every pair of thresholds used on two signals will pro-

vide a corresponding mutual information (MI) value.

By computing the MI value for every pair of thresh-

olds, a MI surface is obtained. In this section, we

present two methods to maximise the MI value. The

ﬁrst method is to use dynamic programming to com-

pute the entire MI surface using all pairs of thresholds

(chosen from two discrete sets). The second method

is to use the simplex algorithm and perform gradient

ascent to ﬁnd the maximum MI value, under the as-

sumption of surface convexity.

3.1 Full Surface Mapping

A brute-force approach to computing the MI surface

involves iterating over all pairs of thresholds (chosen

from two discrete sets), using them to threshold both

signals, then computing the MI between the thresh-

olded signals. If T

thresholds are tried for each sig-

nal, this results in T

pairs and a computation in the

order of O(T

N), where N is signal size (e.g. the

number of pixels in an image). The dynamic pro-

gramming algorithm we describe achieves the same

results in time O(T

+ N ).

DETECTION THRESHOLDING USING MUTUAL INFORMATION

409

Firstly, we denote A = {a

, ..., a

} as the set

of thresholds we wish to evaluate for the ﬁrst sig-

nal and B = {b

, ..., b

} as the set of thresh-

olds we wish to evaluate for the second signal. Next,

we note that equation (3) requires the four values

for p

(u, v), with u, v ∈{0, 1}. p

(u) and p

(v)

can be obtained from these values (e.g. p

(1) =

(1, 0) + p

(1, 1)). Each of these four values

are computed by counting the number of occurances

where x



= u and y



= v, then dividing by the

total number of values, N. Therefore, we wish to

compute these four counts for each pair of thresh-

olds we wish to evaluate. We denote the counts as

u,v

), which equals the number of occurances

where x



= u and y



= v, when the thresholds are

set at T

= a

and T

= b

. Initially the counts

are all set to zero. For each data point we have the

values x

and y

. From these values, we can deduce

that C

0,0

) will be increased by one when both

and b

. Similarly, C

0,1

) will be

increased by one when both a

and b

≤ y

Count maps C

1,0

and C

1,1

have similar rules. For

each data point, we could increase the counters in

each map by iterating over all thresholds that should

be increased. A faster method is to store markers at

the positions in the map where the count increases and

integrate afterwards. This is a similar, complemen-

tary technique to the standard dynamic programming

method used in (Viola et al., 2003) to quickly ﬁnd

the sum of all pixels in a rectangular area of an im-

age. The pseudo-code describing how to update the

count maps for a data-point is shown in ﬁgure 1. Fi-

nally, we integrate the counts horizontally, as follows:

u,v

) ← C

u,v

)+C

u,v

i−1

)

and then vertically,

u,v

) ← C

u,v

)+C

u,v

j−1

)

This array now stores, at location C

u,v

), the

number of occurances where x



= u and y



= v,

when the thresholds are set at T

= a

and T

= b

Using the obtained values, this approach can be used

to compute the entire MI surface using equation (3).

3.2 Simplex Maximum Search

Although the MI surface is not guaranteed to be con-

vex, strong convexity was present in the vast majority

of types of data we have investigated. Any gradient

ascent method will be very computationally efﬁcient,

compared to a full search, even using the above dy-

namic programming strategy. Using a gradient ascent

approach (such as the Simplex algorithm) also has the

advantage that the thresholds do not need to be quan-

tised into discrete values. Any full-search approach

will require a ﬁnite set of pairs of thresholds, therefore

demanding a quantisation of the values. This means

that the Simplex search ﬁnds a more precise optimum

Given: data point (x

, y

)

Find largest threshold a

such that a

≤ x

Find largest threshold b

such that b

≤ y

1,1

)++

1,1

i+1

) −−

1,1

j+1

) −−

1,1

i+1

j+1

)++

1,0

j+1

)++

1,0

i+1

j+1

) −−

0,1

i+1

)++

0,1

i+1

j+1

) −−

0,0

i+1

j+1

)++

Figure 1: Pseudocode for algorithm in subsection 3.1.

solution. Simplex (or another gradient ascent method)

can also be used efﬁciently for higher dimensional

thresholding. For example, if we wished to choose

P thresholds that would maximise the mutual infor-

mation between P thresholded signals, a full-search

would usually be unfeasible for P>2.

3.2.1 Initialisation and Scale

In order to use Simplex, the initial position and sim-

plex size needs to be speciﬁed. The choice of these

parameters may depend on the application. We pro-

pose to initialise Simplex in the following manner, as

it was deemed suitable for our target application of

video processing. In the ﬁrst two video frames, a full

search is performed, using as ﬁne a quantisation as is

possible within the time constraints. The thresholds

found using the full search can be used to initialise

the Simplex search in subsequent frames (i.e. The

thresholds found in the previous frame are used as the

starting position for the current frame). The simplex

size can be determined by setting it to be a fraction

(e.g. 10%) of the change in thresholds between the

ﬁrst two frames. This size can be left ﬁxed or adapted

to minimise convergence time. Alternatively, multi-

ple initialisation positions and scales can be evaluated

to choose the one that provides the greatest MI value.

3.2.2 Convexity Assumption

If there are multiple peaks in the MI surface, sim-

plex will not be guaranteed to ﬁnd the global maxi-

mum. However, by initialising the simplex using the

thresolds of the previous frame, the temporal coher-

ence of the thresholds is enforced, rather than toler-

ating the thresholds jumping between two similarly

MI valued peaks. We also found that multiple peaks

were only likely to occur in two scenarios: either there

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

410

was a correlation between the detectors false posi-

tives/negatives or the signals did not share much mu-

tual information, in which case the peaks were caused

by noise.

3.2.3 Efﬁciency Analysis

In order to gauge how efﬁcient the gradient ascent

approach is compared to the full-search, we calcu-

lated the number of iterations required to converge to

the correct foreground-detection thresholds for each

of 200 frames in a multimodal (thermal infrared and

visible spectrum) video sequence. We used a median

background image for both the visible and infrared

sequences. We initialised our simplex at 10 different

scales. In only two tests (out of 2000) did it converge

to a sub-optimum solution. This occurred at the two

smallest scales. We found that larger scales, in gen-

eral, required more iterations to converge, but were

more likely to converge to a more precise solution.

The average number of iterations to convergence was

26.72. When compared to a full-search, using 256

thresholds for each signal, the Simplex method is over

2400 times faster.

4 EXPERIMENTAL RESULTS

4.1 Foreground Detection

To test our algorithm, we used it to choose thresh-

olds for foreground detection for multi-modal (ther-

mal infrared and visible spectrum) video data. The

surveillance-type video was captured using the a joint

IR-Visible camera rig (

O Conaire et al., 2005). We

used the non-parametric background model described

in (Elgammal et al., 2000) to separately model the

colour and thermal background of the scene. For each

pixel, the models each return the probability that the

pixel belongs to the background. Since we used a lin-

ear quantisation of the threshold space, we got bet-

ter resolution by using the negative logarithm of the

probability. Speciﬁcally, we used min(−log(p), 255)

in the foreground detection map for each pixel, where

p is the background probability. This spread out the

detection values (similar to histogram equalisation),

so that they were not all clumped into one bin.

Our tests were run on three multi-modal sequences

of approximately 850 frames each. Two were daytime

scenes and one was captured at night. In order to eval-

uate our approach to thresholding, we compare the

thresholds produced by our method to those produced

by Kapur thresholding (Kapur et al., 1985). Kapur

et al. also used an information theoretic approach to

thresholding. Using the signal’s histogram, their ap-

proach was to explain positive and negative detections

as two different signals and choose the threshold that

would maximise the sum of the two-class entropies.

In a comparison of thresholding methods (Rosin and

Ioannidis, 2003), Kapur thresholding was determined

to have the best all-round performance. The results of

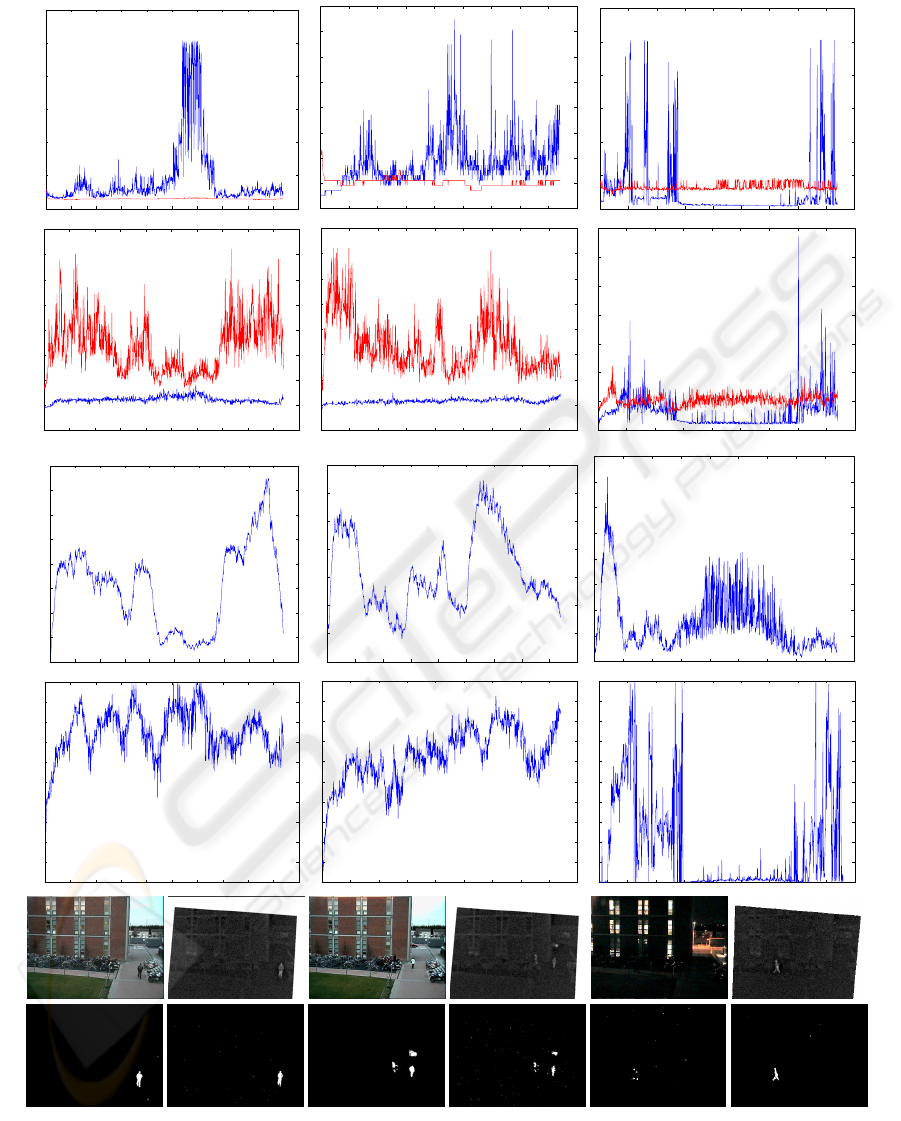
our experiments are shown in ﬁgure 2.

In the daytime scenes, there is strong mutual infor-

mation and the results are good. The Kapur thresholds

behave in exactly the opposite way to our approach.

While the Kapur threshold is very stable in the visible

spectrum, the MI threshold varies signiﬁcantly. On

the other hand, the Kapur threshold is very unstable

in the infrared spectrum, the MI threshold is very sta-

ble. Our method seems to perform counter intuitively,

since the thermal infrared images are far noisier than

the visible spectrum. However, if one imagines two

well separated distributions, as is the case when there

is a high signal-to-noise ratio, then there is a wide

range of thresholds that would give very good perfor-

mance. In a noisy signal, the noise and signal are not

as well separated, so there is only a very narrow band

of thresholds that give the correct separation. This is

why our method has a very stable threshold for the

infrared images, as there is only a very narrow range

of values where the infrared agrees with the visible

spectum. The visible spectrum threshold, on the other

hand, can vary a lot without causing any performance

degradation, since the noise is so low.

In the night time scene, there is very little mu-

tual information between the visible and infrared fore-

ground maps. Pedestrians are practically undetectable

in visible spectrum images. This leads to a low value

at the MI surface peak and poor thresholds for both

modalities. The MI value itself can be used as a qual-

ity measure to determine the reliability of the thresh-

olds returned. However, the mutual information is de-

pendant on how much foreground is present, so we

therefore considered a more robust quality measure

that takes the foreground size into account. If we

compute f , deﬁned as the fraction of all pixels that

both maps agree is foreground, then the highest possi-

ble MI value is M

max

= −f log(f )−(1−f ) log(1−

f). By dividing the obtained MI score by M

max

we obtain a quality (or reliability) measure of the re-

turned thresholds. This quality score was computed

for all sequences and is shown in ﬁgure 2(d).

Future work will involve determining how to cater

for scenarios where the threshold quality score is low.

This scenario could mean that one or both signals are

performing very poorly (such as the visible spectrum

in nighttime scenes), or that there is no mutual infor-

mation to utilise (such as when there are no objects or

people in the scene). One approach could be to revert

to using a single-band thresholding method for each

signal (such as Kapur). Another approach might be to

use the motion information in each of the modalities.

DETECTION THRESHOLDING USING MUTUAL INFORMATION

411

(a)

0 100 200 300 400 500 600 700 800 900 100

0 100 200 300 400 500 600 700 800 90

(b)

0 100 200 300 400 500 600 700 800 900 100

0 100 200 300 400 500 600 700 800 90

(c)

0 100 200 300 400 500 600 700 800 900 100

.005

0.01

.015

0.02

.025

0.03

.035

0.04

0 100 200 300 400 500 600 700 800 90

.005

0.01

.015

0.02

.025

0.03

.035

0 100 200 300 400 500 600 700 800 90

x 10

−3

(d)

0 100 200 300 400 500 600 700 800 900 100

0 100 200 300 400 500 600 700 800 90

(e)

(f)

Figure 2: Comparison of our method to Kapur thresholding. Left and Centre columns are from daytime sequences. Right

column is from a night-time sequence. Rows correspond to: thresholds for (a)Visible Spectrum and (b)Infrared, (c)Mutual

Information, (d)Threshold Quality Measure, (e)Example frames from each sequence, (f)Example thresholded images using

our method. In rows (a) and (b), the Kapur thresholds are shown in red, our method’s thresholds are in blue.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

412

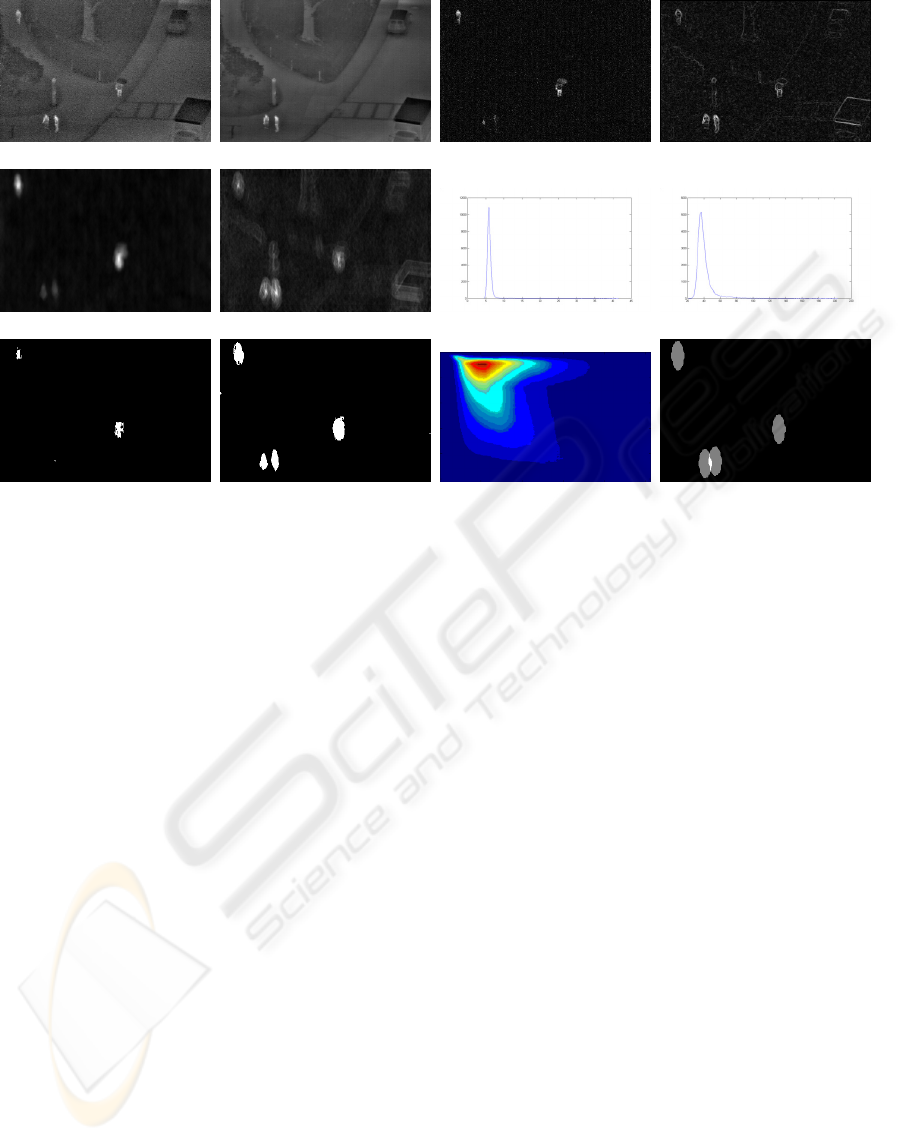
(a) (b) (c) (d)

(e) (f) (g) (h)

(i) (j) (k) (l)

Figure 3: Person-detection example: (a)Current image, (b)Background image, (c)Background difference, (d)Image edges,

(e)Silhouette detection map, (f)Contour detection map, (g)Histogram of (e), (h)Histogram of (f), (i)Kapur thresholded result,

(j)Our method, (k)Mutual information surface, (l)Detected People.

4.2 Person Detection

To further test our algorithm, we incorporated it into

a person detection system and used the OSU Thermal

Pedestrian Database from the OTCBVS Benchmark

Dataset (Davis and Keck, 2005) to evaluate perfor-

mance. The database contains images of pedestrians

taken with a thermal infrared camera in a wide variety

of environments. Since our goal was to evaluate the

thresholding component of the system, the other com-

ponents were chosen to be as simplistic as possible.

The system worked as follows. First, the median

background image was computed. Then for each im-

age, two detectors were used: one based on pedestrian

contour and the other based on silhouette. The con-

tour detection map was obtained by convolving the

pedestrian contour template with the Sobel edges of

the image. The silhouette detection map was obtained

by convolving the pedestrian silhouette template with

the absolute difference image between the current im-

age and the background image. Thresholds for these

maps were obtained using our mutual information

thresholding algorithm (subsection 3.1). Pedestrian

regions were determined as all pixels that had above

threshold values in both maps. Next, each local max-

ima in the contour detection map within these regions

was paired with the closest local maxima in the sil-

houette detection map within these regions. Maxima

in the silhouette detection map were then paired with

the closest maxima in the contour detection map. Per-

son candidates corresponded to each pair of maxima,

from the two separate maps, that were both paired to

each other (i.e. they were both closest to each other).

Candidates were then evaluated according to the min-

imum description length principle, in respect to how

much of the pedestrian regions they could explain.

We use a pedestrian candidate template to evaluate the

ﬁtness of each candidate by calculating the maximum

number of pedestrian-region pixels it overlaps with,

when centred on either maxima of the candidate. The

best candidate is considered a ‘true’ person and the

pedestrian region pixels it overlaps are removed. This

process continues until there are no remaining candi-

dates, or no candidate can explain more than a pre-

deﬁned number of pixels (which was set at one tenth

of the template size).

We used the dynamic-programming full-search

thresholding algorithm and it performed well for al-

most all images. For some images, there were two

peaks in the MI surface. We speculate that this ex-

tra peak was due to the correlation between the noise

in both detection maps, since they were both derived

from the same image. This peak was usually smaller

than the correct peak but it was occasionally greater.

We catered for this scenario by evaluating all local

maxima in the surface and evaluating them in order

DETECTION THRESHOLDING USING MUTUAL INFORMATION

413

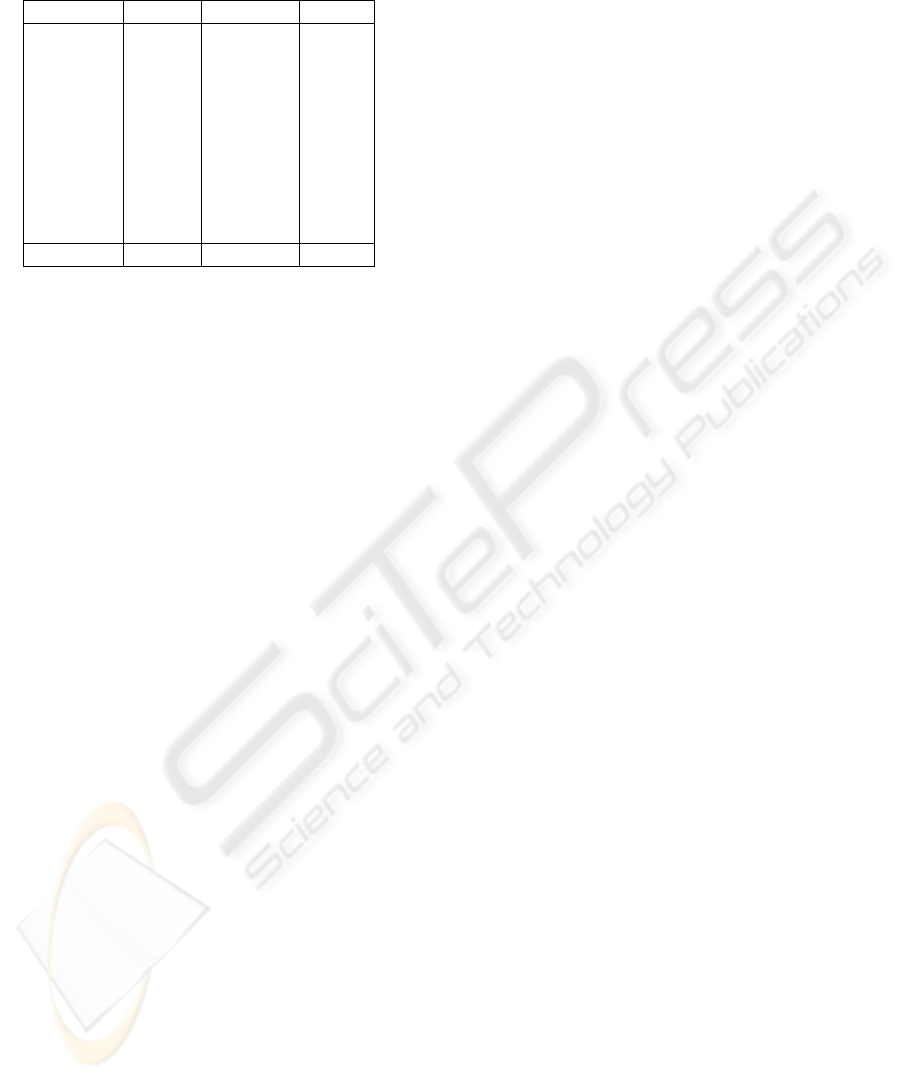
Table 1: The results of our pedestrian detection system on

the OTCBVS database are shown below.

Sequence People Precision Recall

1 91 0.95 0.98

2 100 0.95 0.98

3 101 0.87 1.00

4 109 0.94 1.00

5 101 0.92 0.96

6 97 0.98 1.00

7 94 0.93 0.99

8 99 0.97 0.99

9 95 1.00 1.00

10 97 0.92 0.98

Total 984 0.95 0.99

of descending MI score. We discarded peaks whose

thresholds produced binary maps with very high Euler

numbers (an Euler number of a binary image is the

number of regions minus the number of holes and can

be calculated quickly using local pixel information.

A high value indicates high noise). An example of

person detection is shown in ﬁgure 3. In this difﬁcult

example, the two people, in the bottom left of the im-

age, have been standing in the same spot for the entire

sequence, so have been included in the background

image. However, the motion of the people leaves an

impression on the difference image and hence, on the

silhouette based detector map. Our method causes the

silhouette threshold to drop so that it agrees with the

strong detection in the contour-based detection map.

Kapur, on the other hand, sets the two thresholds inde-

pendently and therefore fails to detect all the people.

The results of our system are shown in table 1. They

are comparible to those obtained in (Davis and Keck,

2005).

5 CONCLUSION AND FUTURE

WORK

In this paper, we introduced a novel non-parametric

thresholding method that chooses two detection

thresholds for two input signals so that the mutual

information between the thresholded signals is max-

imised. We described two efﬁcent implementations of

our algorithm using dynamic programming for a full-

search and Simplex gradient ascent for a faster search

with the assumption of surface convexity. We evalu-

ated our method by comparing it to a standard non-

parametric thresholding algorithm using multi-modal

video sequences. We also incorporated our method

into a person detection system and achieved good re-

sults using the publicly available OTCBVS pedestrian

database.

Our thresholding method works on aligned data so

can be used for local, as well as global threshold-

ing. It can also be used to threshold space-time slices,

such as groups of video frames. In these scenarios,

the window size is an important parameter: too small

and it may be sensitive to noise, too large and there

is a chance the signal properties have changed and a

global threshold would not be appropriate. Investigat-

ing how the window sizes should be set automatically

is an interesting area of further work.

Determining the types of data that can be used with

our method is another area for future studies. Sources

that are completely independent do not share any mu-

tual information and therefore are not suitable. On the

other hand, data sources that are linearly dependent

will produce thresholds equal to the median data val-

ues, as this maximises their mutual information. In-

dependence in the noise of both sources would seem

an important factor to ensure that good thresholds are

produced. The use of derivatives, such as edges, as a

second data source to select thresholds, has proven

useful, although it may violate the noise indepen-

dance criterion. Similarly, using two sources of data

that come from the same sensor (the red and green

colour bands, for example), may also violate this cri-

terion and produce multiple peaks in the MI surface.

In small-scale experiments for foreground detection,

using a combination of two colour bands, or using

the edges of the absolute difference map as a second

source, our method produced good thresholds, so fur-

ther testing is required to evaluate when these sources

might fail.

The results of our pedestrian detection system were

encouraging. However, the OTCBVS pedestrian data-

base does not contain much clutter, so a future system

will be tested on more difﬁcult pedestrian data, using

multi-modal data we have captured.

Currently, our method does not consider spatial in-

formation or the proximity of pixels when choosing

the thresholds. Incorporating this information into our

method is another avenue of research to consider. For

example, the two parameters (low and high thresh-

olds) for hysteresis segmentation could be selected by

maximising the MI between the resulting segmenta-

tion and another source of data.

Finally, using this method on three or more sources

of data is another area for future investigation. The

quality measure we developed gives a estimate of the

reliabillity of the results and hence, this might be used

to make a system more robust against the failure of

one or more components, if it can quickly detect un-

reliability in the data sources. The combination of

three or more sources provides many interesting chal-

lenges, such as whether they should all be combined

simultaneously, or whether a pair-wise combination,

using the quality values returned, provides better per-

formance.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

414

ACKNOWLEDGMENTS

This material is based on works supported by Science

Foundation Ireland under Grant No. 03/IN.3/I361

and sponsored by a scholarship from the Irish Re-

search Council for Science, Engineering and Tech-

nology (IRCSET): Funded by the National Develop-

ment Plan. The authors would also like to express

their gratitude to Mitsubishi Electric Research Labs

(MERL) for their contribution to this work.

REFERENCES

Davis, J. and Keck, M. (2005). A two-stage template ap-

proach to person detection in thermal imagery. In

Workshop on Applications of Computer Vision, vol-

ume 1, pages 364–369.

Duda, R. O., Hart, R. E., and Stork, D. G. (2001). Pattern

Classiﬁcation. John Wiley & Sons, 2nd edition.

Elgammal, A., Harwood, D., and Davis, L. (2000). Non-

parametric model for background subtraction. In Pro-

ceedings of the 6th European Conference on Com-

puter Vision.

Kapur, J., Sahoo, P., and Wong, A. (1985). A new method

for graylevel picture thresholding using the entropy

of the histogram. Computer Graphics and Image

Processing, 29(3):273–285.

Kruppa, H. and Schiele, B. (2001). Hierarchical combina-

tion of object models using mutual information. In

BMVC.

Nelder, J. and Mead, R. (1965). A simplex method for func-

tion minimization. The Computer Journal, 7:308–

313.

O Conaire, C., Cooke, E., O’Connor, N., Murphy, N., and

Smeaton, A. F. (2005). Fusion of infrared and visible

spectrum video for indoor surveillance. In Interna-

tional Workshop on Image Analysis for Multimedia In-

teractive Services (WIAMIS), Montreux, Switzerland,.

Otsu, N. (1979). A threshold selection method from gray-

level histogram. IEEE Transactions on System Man

Cybernetics, 9(1):62–66.

Peng, H., Long, F., and Ding, C. (2005). Feature selec-

tion based on mutual information: Criteria of max-

dependency, max-relevance, and min-redundancy.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 27(8):1226–1238.

Pluim, J., Maintz, J., and Viergever, M. (2003). Mutual-

information-based registration of medical images: a

survey. IEEE Transactions on Medical Imaging,

22(8):986–1004.

Rosin, P. (1998). Thresholding for change detection. In

IEEE International Conference on Computer Vision,

pages 274–279.

Rosin, P. and Ioannidis, E. (2003). Evaluation of global im-

age thresholding for change detection. Pattern Recog-

nition Letters, 24(14):2345–2356.

Rosin, P. L. (2001). Unimodal thresholding. Pattern Recog-

nition, 34(11):2083–2096.

Viola, P., Jones, M. J., and Snow, D. (2003). Detecting

pedestrians using patterns of motion and appearance.

In IEEE International Conference on Computer Vision

(ICCV), volume 2, pages 734–741.

Viola, P. A. (1995). Alignment by Maximization of Mutual

Information. Phd thesis, Massachusetts Institute of

Technology, Massachusetts (MA), USA.

DETECTION THRESHOLDING USING MUTUAL INFORMATION

415