
IMPLEMENTATION STRATEGIES FOR “EQUATION GURU”
A User Friendly Intelligent Algebra Tutor
Senay Kafkas, Zeki Bayram
Computer Engineering Department, Eastern Mediterranean University
Famagusta, North Cyprus
Huseyin Yaratan
Educational Science, Faculty of Education, Eastern Mediterranean University
Famagusta, North Cyprus
Keywords:
Intelligent Tutoring Systems, Intelligent Learning Environments, Equation Solving.
Abstract:
We describe the implementation strategies of an intelligent algebra tutor, the “Equation Guru” (EG), which
is designed to help students learn the concepts of equation solving with one unknown. EG provides a highly
interactive and entertaining learning environment through the use of Microsoft Agents. It consists of two main
parts. The first is the “Tutorial” part where students are guided through the steps of solving equations with
one unknown. The second, “Drill and Practice” part gives them a chance to practice their skills in equation
solving. In this part, equations are automatically generated by EG, and presented to the student. EG monitors
the student’s performance and adjusts the difficulty level of the equations accordingly.
1 INTRODUCTION
In the last decade, “computer-aided instruction”
(CAI) systems, which had the drawback of not be-
ing individualized to the learners’ needs and which
could not provide the same kind of attention that a
student receives from a human tutor, have been re-
placed with “intelligent tutoring systems” (ITSs). An
ITS is a complex software program that uses artificial
intelligence and pedagogical techniques to store and
use domain-specific knowledge, model the learner’s
behaviour, and tutor the student in its area of exper-
tise. The primary goal of an ITS is to achieve effective
teaching by emulating the behaviour of a human tutor.
It does so by “working” with the student on a one-to-
one basis, monitoring the student’s performance and
progress, making pedagogical decisions about how to
teach, and providing feedback and remedial material
when appropriate to the student.
ITSs have proven highly effective at increasing
students’ performance and motivation (Koedinger,
1998), (Martin et al., 2001), (Mayo, 2001), (Mitro-
vic et al., 2004). In this paper, we describe the im-
plementation strategies of an intelligent algebra tutor,
called Equation Guru (EG), that tutors in the domain
of equation solving with one unknown. EG is de-
signed for helping high school students at grade 8.
Microsoft Agents are used all throughout EG for
the interaction of the system with the student. These
animated characters can speak, make gestures, and
understand spoken words, although we have not used
speech understanding in EG due to the limited nature
of the speech understanding capability of the agents.
The agent both provides immediate feedback on the
current problem at hand, and also motivates the stu-
dent through encouraging words (e.g. “Well done,
Jane!”) and animations (e.g. clapping), leading to
a highly interactive learning environment.
EG consists of two main parts: The “Tutorial” part
and the “Drill and Practice” part. The goal of the
“Tutorial” part is to teach the student the concept of
equations, as well as the steps required to solve equa-
tions. It achieves this in an interactive manner with
Microsoft Agents and dialogs . The dialogs that are
used in this part are similar to the ones observed in a
real classroom setting. The “Tutorial” part is further
divided into sections. One of the sections includes a
game, based on the “beam balance” analogy. In the
other sections, step by step, the students are taught
how to solve equations and are prepared for the “Drill
and Practice” part. For the details of the “Tutorial”
part, the reader is referred to (Kafkas et al, 2005).
The “Drill and Practice” part runs in three modes.
The first (main) mode makes use of the “Student Di-
agnostic” and the “Pedagogical” modules. It stores
the student’s actions and then makes pedagogical de-
cisions (like determining the level of next question)
according to the student model. In the second mode,
58
Kafkas S., Bayram Z. and Yaratan H. (2006).
IMPLEMENTATION STRATEGIES FOR “EQUATION GURU” - A User Friendly Intelligent Algebra Tutor.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - AIDSS, pages 58-65
DOI: 10.5220/0002488500580065
Copyright
c
SciTePress
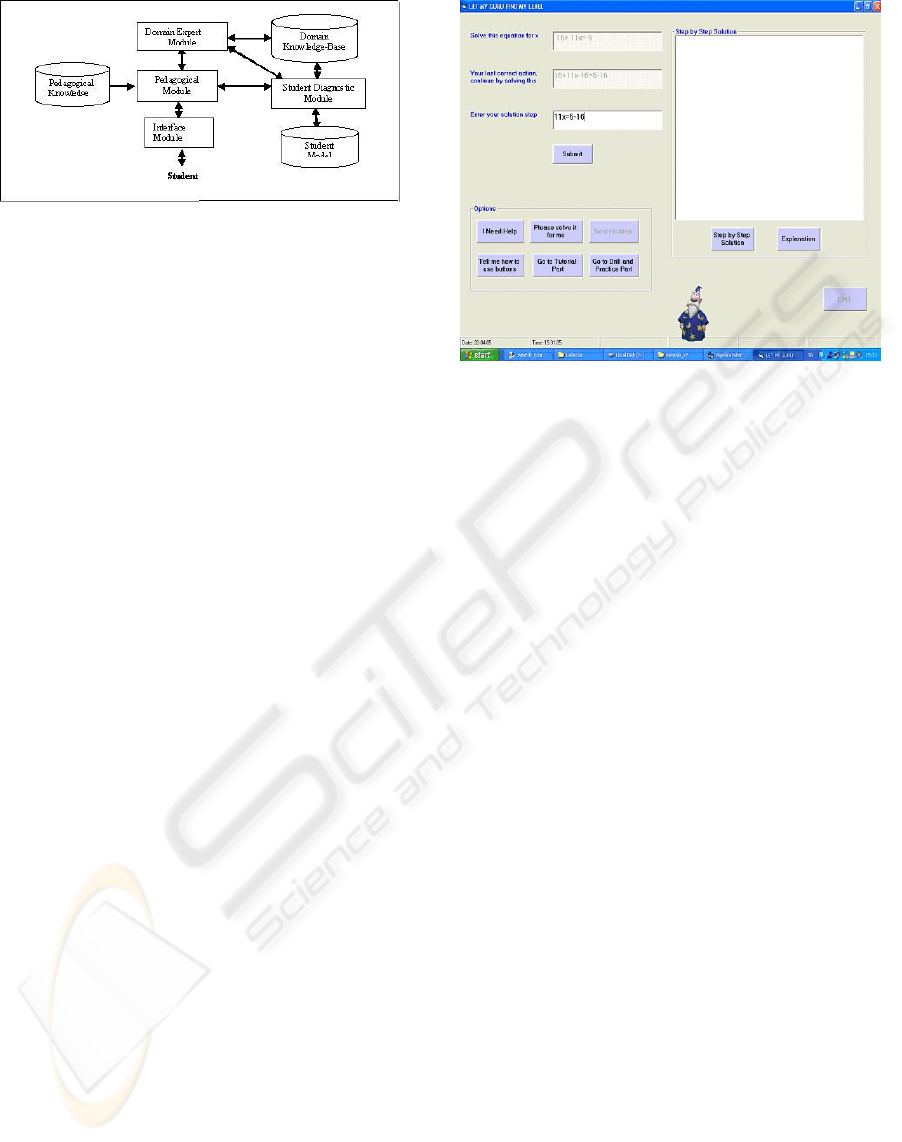
Figure 1: Overall architecture of the “Drill and Practice
part”.
the student can pose an equation to EG, view the step
by step solution and hear the explanation. In the third
mode, the student can choose a level, get an equation
from that level and try to solve it.
The rest of the paper is organized as follows. In
section 2, we describe in detail the implementation
of EG’s “Drill and Practice” part. This includes the
user interface, domain expert, student diagnostic and
pedagogical modules. In section 3, we compare EG to
other equation solving ITSs. Finally, in section 4 we
have the conclusion and future research directions.
2 THE “DRILL AND PRACTICE”
PART
The aim of this part is to enable students to drill and
practice based on what they have learned in the “Tu-
torial” part. The architecture of this part is given in
Figure 1, which in fact is common to most intelligent
tutoring systems. There are four components in this
architecture: “Domain Expert,” “Pedagogical,” “In-
terface” and “Student Diagnostic” modules. Further-
more, this part runs in three different modes. We ex-
plain the modes, as well as the modules, in the fol-
lowing sections.
2.1 The Three Modes of the “Drill
and Practice” Part
The first mode, named “Let my Guru find my level,”
is fully automated. It includes all the modules de-
picted in Figure 1. The equation to be solved and the
action to be taken next (such as whether hints will be
generated, or whether some encouragement will be
given) is determined by consulting the student model
and making use of pedagogical knowledge about the
tutoring process. Figure 2 is the screenshot of this
mode.
In the second mode, “I will specify the equa-
tion,” the student poses an equation to be solved, and
Figure 2: Mode 1 of the “Drill and Practice” part - “Let my
Guru find my level”.
watches the system solve the equation in a step-by-
step fashion and hears the explanation of each step.
In the third mode, “Let me specify my level,” the
student can choose the level of difficulty of the equa-
tion to be generated, and the equation is generated at
the specified level of difficulty for the student to solve.
The three modes of the “Drill and Practice” part
provide a very flexible environment in which students
can improve their equation solving skills.
2.2 The “Domain Expert” Module
The “Domain Expert” module is the “technical ex-
pert” of EG. It acts as the lexical analyzer, problem
solver and evaluator. Its job is to solve equations with
one unknown. It uses the “Domain Knowledge-Base”
which stores knowledge about solving linear equa-
tions with one unknown in the form of rules in the
Prolog programming language.
2.2.1 Inner Representation of Equations
The “Interface” module of EG is capable of represent-
ing equations as strings. But these strings should be
passed to the Prolog side and understood by the sys-
tem somehow. The “Domain Expert” module con-
verts string equations to their corresponding inner
representations. Table 1 represents corresponding in-
ner representations of terms and expressions.
Some examples of equations and their correspond-
ing representations are provided by Table 2.
In addition to this, the inner representation of an
equation is converted back into string form by the
“Domain Expert” module, since the equations are pre-
sented to the user end in the string form.
IMPLEMENTATION STRATEGIES FOR “EQUATION GURU” - A User Friendly Intelligent Algebra Tutor
59

Table 1: Inner representation of expressions.
Term/Expression Inner Representation
N, N is positive integer n(N)
N, N is negative integer nn(N)
x v(x)
-x nv(x)
Cx, C is positive integer coeff(C,x)
Cx, C is -ve integer ncoeff(C,x)
+ plus(Term1,Term2)
- Minus(Term1,Term2)
* Times(Term1,Term2)
/ div(Term1,Term2)
Table 2: Some examples of equations and their inner repre-
sentation.
Equation Corresponding inner representation
5+x=10 eq(plus (n(5),v(x)), n(10))
5-2x=10 eq(minus (n(5),coeff(2,x)), n(10))
-5-2x=-x eq(minus (nn(5),coeff(2,x)), nv(x)
3x/7 =10 eq(div(coeff(3,x)),n(7)), n(10))
2.2.2 Lexical Analysis
The Equation Guru’s alphabet consists of the follow-
ing set of symbols: { 0,1,2,3,4,5,6,7,
8,9,x,=,+,-,/}. If an entry that contains
some symbol that is not in this set, the system will
warn the student. Figure 3 demonstrates how lexical
analysis is done. The predicate analyse takes the
student’s entry as input and returns the result of the
lexical analysis (Status). Simply it checks if the
provided string can be parsed (by predicate a ) and
has any unknown, x (by hasX) or not. The status is
either ok or lexical error.
2.2.3 Correctness Analysis
If the student’s entry is lexically correct, then it
will be evaluated to check for correctness. Figure
4 depicts how the “Domain Expert” checks correct-
ness. The predicate evaluate takes student’s in-
put (Studinput) and EG’s input (Tutinput)
then gives the evaluation results. The variable
Correctness shows if the submitted step is cor-
rect or not and Solved shows if the equation is
solved (i.e. x=“something”) by the entered step.
When the student provides his/her solution step
Figure 3: Lexical Analysis.
Figure 4: Correctness Analysis.
(Studinput) in string form, evaluate gets
this input, then the predicate FindWhich returns
the inner representation of the equation (Tuteq1)
and the required step (Stepname) to move ahead.
Stepname will be used by evaluate in order to
determine if the given equation is solved by the sub-
mitted step or not. The correctness analysis is done by
the predicates solution and dogrumudur. The
predicate solution is called two times. The first
one gets the student’s solution step (Studinput)
and returns the final result (Studout). The sec-
ond one gets the equation asked at the beginning to
the student (Tutinput) and returns the final re-
sult (Tutout). The predicate dogrumudur sim-
ply checks if the student’s input is a right step on way
going to the solution or not. If it is a right step then
the argument (Correctness) will be equal to 1,
otherwise to 0. Similarly, if the equation is solved by
the submitted step, then Solved will be assigned to
1, otherwise to 0.
2.2.4 Equation Solving
Equation solving is an iterative process. Appropri-
ate mathematical operations (like dividing, adding
like terms, balancing the equation, expanding etc.)
are applied on each step until value of the unknown
has been found. Figure 5 is a piece of code from
EG which shows how the “Domain Expert” mod-
ule solves the equations in a recursive manner, sim-
ulating the iterative process. Notice that the predi-
cate solve calls itself. It gets the equation (Equ)
in its inner form, applies the appropriate operation,
and then returns resultant equation (NE) and solution
(S). The predicate GetEqMakeStr gets the equa-
tion (Equ) and converts it to the string form. Af-
ter the conversion process, the predicate FindWhich
gets the equation in the string form and returns the
appropriate step (Stepname) and inner representa-
tion of the equation (Equ2). Once the appropriate
step is obtained, the predicate operation gets the
step (Stepname) and equation (Equ2) and then
returns resultant equation (NE) and solution (S).
The resultant equation (NE) will be used by the pred-
icate solve until a solution has been found.
2.3 The “Pedagogical” Module
The “Pedagogical” module is the one that runs the
show, making use of the services of the “Domain Ex-
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
60

Figure 5: Equation solving in EG.
pert,” “Student Diagnostic” and “Interface” modules.
2.3.1 Deciding on the Next Action
The “Pedagogical” module applies pedagogical
strategies, stored in the “Pedagogical Knowledge”
component, to the current situation at hand to decide
on the next action. Whenever the student submits a
solution step in the form of a revised equation, it asks
the “Domain Expert” whether the submitted equation
is equivalent to the previous one (i.e. if it has the same
solution as the previous one). If indeed it preserves
the solution, this time the “Domain Expert” checks
whether the student’s response represents a move in
the right direction toward solving the equation or not.
If the student has moved away from finding a solu-
tion by making the equation more complex, s/he is
warned, but allowed to continue trying to solve the
equation. However, if the equation entered by the
student does not preserve the solution to the origi-
nal equation, then the “Student Diagnostic” module
is notified, which determines the error and updates the
“Student Model” accordingly. In such a case, the ser-
vices of the “Interface” module are used to notify the
student of the error and display hint messages.
As an example, the hint message generated for the
equation 3x+2=1 is “balance the equation.” An exam-
ple of an error message is “you should have balanced
the equation” where the “Pedagogical” module deter-
mines that the student couldn’t balance the equation.
2.3.2 Generating Explanations
The “Pedagogical” module of EG is capable of pre-
senting a step by step solution to the student by in-
teracting with the “Domain Expert” module. The ex-
planation of solution steps is specific to the equation
under consideration.
In Figure 6, we see the Guru explaining a step in
the solution of an equation.
2.3.3 Equation Generation
Another job of the “Pedagogical” module is to gen-
erate the equations at a suitable level for the stu-
dent. The equations are randomly generated at a given
level. The complexity of the equations increases from
level 1 to level 35. Figure 8, given in the appendix,
depicts these levels.
Figure 6: Explanations presented to the student.
When a new student logs on the system, his/her
level is started at level 1. If the student has logged into
the system before, the system remembers his/her last
level. In both cases, if the student provides two con-
secutive correct answers, then the level is increased
by one. If the student makes 5 errors of any type (see
Table 3 for the error types) then his/her level will be
decreased by one. Otherwise the level will remain
same.
The first 4 levels are in the form of a+x=b. The
first level is the simplest one since the unknown will
be obtained as a positive integer. In the second level,
again the unknown is a positive integer but this time
the numbers (a and b) are bigger than the previous
level’s. In level 3, the result (x), is a negative integer
and similarly in level 4, bigger numbers are used.
From level 5 to 8, the equations are in the form of
a-x=b. In the fifth and sixth levels, b is greater than a,
but is the rest up to 8, a is greater than b.
Beginning with level 9, the equations are created
without any regard to how big the number is. If the
student has reached to this level then s/he should be
comfortable with big numbers.
From level 9 to 12, the equations are in the form of
b+ax=c. In level 9 and 10 the numbers are chosen in
such a way that the unknown x will be obtained as a
positive and negative integer respectively. In level 11,
the result will be a positive fraction and in level 12 the
result will be a negative fraction.
From level 13 to 16, the equations are in the form
of b-ax=c. In levels 13 and 14, the x will be obtained
as positive and negative integer respectively. In level
15 the unknown will be positive fraction and in level
16, it will be negative fraction. After level 16, the
equations are generated without taking into account
the result of the unknown. Similarly, it is assumed
that if the student has managed to reach that level than
s/he is comfortable with fractions and positive/ nega-
IMPLEMENTATION STRATEGIES FOR “EQUATION GURU” - A User Friendly Intelligent Algebra Tutor
61

tive results.
For the equations in levels 17 to 22, the operation
“add like terms” is required. The difference between
these levels is the places of unknowns. For the equa-
tions in levels 23 to 31, the operation “cross multipli-
cation” is required. The complexity is increased by
generating equations with negative numbers and un-
knowns in each level.
The equations that belong to levels 31-35 require
“fraction addition.” Similarly the complexity is in-
creased by changing + signs to - signs.
2.4 The “Student Diagnostic”
Module
The “Student Diagnostic” module maintains a model
of the student. This involves keeping track of the stu-
dent’s current level of knowledge, his/her progress as
well as the average solving time, the number of ques-
tions directed, the number of correctly solved ques-
tions, the number of could not be solved questions,
the kinds of errors he/she has been making at each
level.
2.4.1 Error Processing
Table 3 depicts the error types in EG. “Lexical” errors
are coded as E1. Error codes from E2 to E11 are as-
signed to operational errors such as division, adding
like terms, simplification, etc. The error codes are
used during the modeling process of the student.
Table 3: Error Codes and Error Types in EG.
Error Code Error Type
E1 Lexical Error
E2 Add like terms
E3 Balance the equation
E4 Division
E5 Simplification
E6 Multiply both side by -1
E7 Solution
E8 Expansion
E9 Cross multiplication
E10 Find common denominator
E11 Add fractions
2.4.2 Error Analysis
If the student provides a wrong solution step, then
the system will investigate the error type. In Figure
7, the predicate FindError gets the provided so-
lution step from the student (Studinput), as well
as his/her last correct action (Previnput) and re-
turns the error type (Errorname). In order to find
Figure 7: Error Analysis in EG.
the error type, the predicate FindWhich is called
two times. It gets the equation in string form in its
first argument, and returns (in its second argument)
the equation in its inner representation form, and the
expected step name (in its third argument) that should
be applied in order to solve the equation. Lastly, the
predicate fe gets these step names and determines the
error type (Errorname).
2.5 The “Interface” Module
The “Interface” module consists of two parts. The
first part is designed for students’ interactions and the
second part is designed for the instructor.
2.5.1 Student Interaction with EG
In a learning environment, life-like interaction is a
very important aspect. Early ITSs were implemented
without this feature. To remedy this situation ped-
agogical agents were developed. In computer-based
learning environments, pedagogical agents appear to
the students as animated characters and facilitate their
learning process by interacting with them (Shawn et
al., 1999). They achieve this by engaging the student
in a continuous dialogue, emulating the aspects of di-
alogue between a instructor and student, giving the
impression of being life-like and believable, appear-
ing to the user as natural, knowledgeable, attentive,
helpful, concerned, etc (Lester et al., 1997). The ef-
fect of pedagogical agents on students’ learning has
been investigated in (Lester et al., 1997), where it is
shown that life-like characters have a strong positive
effect on the learning process in an interactive learn-
ing environment .
EG uses Microsoft Agents as its main communica-
tion medium. These animated characters are able to
motivate the student in many ways. They congratu-
late the student for a correct move. They warn the
student in a friendly way in case of mistakes, without
discouraging him/her and guide him/her towards a so-
lution through helpful hints. Furthermore, the agents
display interesting characteristics and use body lan-
guage, both to entertain, and engage the student to the
equation solving process.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
62

2.5.2 Instructor Interaction with EG
The second part of the “Interface” module is designed
as a tool for the instructors. They can initiate the
student model of a student and view their students’
progress. Initiating the student model of a student cor-
responds to recording his/her personal information.
3 COMPARISON OF EG WITH
OTHER EQUATION SOLVING
TUTORS
This section compares Equation Guru with other
equation solving tutors. For this comparison only
equation solving tutors in the domain of linear equa-
tions are considered.
Some equation solving tutors’ domains are re-
stricted to equations in some specific form. For in-
stance, Equation Solving Tutor (EST) (Ritter et al.,
1995) helps students in solving linear equations only
in the form of ax+b=c, while in E-Sit (Prince,2004),
the equations are only in the form of ax+bx=c. An-
other tutor, E-Tutor (Razzaq et al., 2004) supports
cross multiplication and expansion in the domain
of linear equations while AlgeBrain (Alpert et al.,
1999) has these features in the domain of linear and
quadratic equations. Different from these tutors, EG
supports all forms of linear equations, including equa-
tions with fractions. Furthermore, the format of equa-
tions is not restrictive - anything is accepted, as long
as it represents a valid equation.
Motivation and attracting the attention of the
learner are important aspects of the learning process.
In order to motivate the student, E-Sit uses a game.
The game window appears automatically whenever
the student gets a specific mark from the posed ques-
tions and the duration of the game depends on the stu-
dent’s success. AlgeBrain uses a character in its tutor-
ing process. Animation features of this character are
limited and it has no speech capability. EG uses Mi-
crosoft Agents for motivating and attracting the atten-
tion of the student which provides a highly effective
learning environment. These characters have a wide
range of animations and they can speak and easily en-
gage the student to the learning process.
E-tutor tutors in a dialog-based manner. Similarly,
the “Tutorial” part of EG is designed in this manner.
In all of the above mentioned equation solving tu-
tors, next problem selection is based on the informa-
tion available in the student model. EG also works
this way. In E-Sit, however, next problem selection
is based on a utility function which does not support
exactly student dependent tutoring.
AlgeBrain is a web-based and collaborative equa-
tion solving tutor while other tutors, including EG are
standalone applications.
Hint messages in Cognitive Tutor (Koedinger et al.,
2000) are generated sequentially to the student. It al-
ways provides a strong hint, by telling exactly what
to do at the end of the sequence. But this approach
contradicts with the principles of effective teaching
identified in (VanLehn et al., 1998). That is, the tu-
tor should not provide strong hints for the solution
of equations when students need them. If so, then
they may miss the opportunity to learn how to solve
equations when they are provided an answer and not
allowed to reason for themselves. EG generates an
appropriate hint message to the student when needed
but this message will never be strong.
In E-Sit, the next expected action (next step) from
the student is specific. For example, for the equation
3x-5=15, the next expected action is 3x=15+5. Also,
the name of the solution step (like transformation, ad-
dition, etc) must be submitted to the system by the stu-
dent. The correctness analysis of the student’s action
is based on this assumption. In such a system, if the
student submits a correct solution step ahead of the
expected one (x=20/3, for the above example), then
the ITS will consider this unexpected step as wrong
solution step. Therefore, the wrong evaluation will
yield a wrong student model. Furthermore, wrong
modeling will yield wrong pedagogical decisions and
strategies. In AlgeBrain, the next expected action is
a set of possible actions that can be applied to sim-
plify the considered equation. This discussion brings
us to a major point of strength in EG, when compared
to other equation solving tutors. In EG, the expected
solution step from the student is not specific. As long
as the student’s action results in an equation with the
same solution as the equation provided by the system,
it is assumed to be a correct move, and the student is
allowed to carry on. However, the student is warned if
his/her solution step takes him away from obtaining a
correct answer. Also, there is no need for the student
to provide the step name to the system.
Furthermore EG supports linear equations in a va-
riety of forms, including those with fraction additions
(this feature is missing in many other tutoring sys-
tems), and a blackboard at the right top corner of the
screen where solutions are displayed, creating a fa-
miliar medium, similar to a classroom learning envi-
ronment.
4 CONCLUSION AND FUTURE
RESEARCH DIRECTIONS
In this paper, we described the implementation strate-
gies of an intelligent tutoring system, called Equation
Guru (EG), which is designed to help high school
students at grade 8 with algebra. EG is an ITS that
IMPLEMENTATION STRATEGIES FOR “EQUATION GURU” - A User Friendly Intelligent Algebra Tutor
63

teaches cognitive skills needed for the solution of lin-
ear equations with one unknown. Equation Guru tu-
tors in a truly interactive manner. This is achieved
through the use of life-like animated characters, Mi-
crosoft Agents, which provide a unique, entertaining
experience to the users of the system.
There are two main parts in EG. In the first (“Tu-
torial”) part, the students are taught how to solve lin-
ear equations with one unknown. Students are then
directed to the “Drill and Practice” part which pro-
vides three modes for students to practice their skills
in equation solving. This “Drill and Practice” part has
been the main focus of this paper.
Future work on EG includes adapting it to be Web
enabled in order to support distance education, and
adding robust natural language processing and under-
standing capability to it in order to make the experi-
ence of using it even more realistic and enjoyable.
REFERENCES
Koedinger, K.R. (1998). Intelligent Cognitive Tutors as
Modeling Tool and Instructional Model. In NCTM
Standards 2000 Technology Conference. Carnegie
Mellon University, Pittsburgh.
Martin, B. et al. (2001). Constraint-Based Tutors: a suc-
cess story. In Journal of Lecture Notes in Computer
Science. 2070 931–940.
Mayo, M.J. (2001). Bayesian Student Modeling and
Decision-Theoretic Selection of Tutorial Actions in
Intelligent Tutoring Systems. University of Canter-
bury, Christchurch, New Zealand.
Mitrovic, A. and Suraweera, P. (2004). An Intelligent Tu-
toring System for Entity Relationship Modeling In
International Journal of Artificial Intelligence in Edu-
cation. 14 375–417.
Ritter, S. and Anderson, J. R. (1995). Calculation and strat-
egy in the equation solving tutor. In Proceedings of
the Seventeenth Annual Conference of the Cognitive
Science Society,Hillsdale, NJ: Lawrence Erlbaum As-
sociates, 413–418.
Prince, R. (2004). E-SIT: An Intelligent Tutoring Sys-
tem for Equation Solving. Retrieved September,2004,
from http://www.amzi.com/articles/e-sit.doc.
Razzaq, L. and Heffernan, N.T. (2004). Tutorial dialog in
an equation solving intelligent tutoring system. In
Workshop on Dialog-based Intelligent Tutoring Sys-
tems: State of the art and new research directions at
the 7th Annual Intelligent Tutoring Systems Confer-
ence,Maceio, Brazil.
Alpert, S.R. and Singley, M.K. and Fairweather, P.G.
(1999). Deploying Intelligent Tutors on the Web: An
Architecture and an Example. International Journal
of Artificial Intelligence in Education,10 183–197.
Koedinger, K.R. and Corbett, A. and Ritter, S. and Shapiro,
L. (2000). Carnegie Learning’s Cognitive TutorTM:
Summary Research Results”. Carneige Mellon Uni-
versity.
VanLehn, et al. (1998). What Makes a Tutorial Event Ef-
fective?. In Proceedings of the Twenty-first Annual
Conference of the Cognitive Science Society.
Shaw, E. and Johnson, W.L. and Ganeshan, R. (1999). Ped-
agogical Agents on the Web. In Proceedings of the 3rd
annual conference on Autonomous Agents, 238–290.
Lester, J. et al. (1997). The Persona Effect: Affective Im-
pact of Animated Pedagogical Agents. In Proceedings
of CHI ’97, Atlanta, 359–366.
Kafkas, S. and Bayram, Z. and Yaratan, H. (2005). A User
Friendly Intelligent Algebra Tutor. In Proceedings of
the 5th International Educational Technologies Con-
ference (IETC’05), Sakarya, Turkey.
APPENDIX
A Difficulty Levels in Equation
Guru
Please refer to the next page for the table containing
the levels of difficulty of equation problems in Equa-
tion Guru.
ICEIS 2006 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
64

Level Sample Equation General shape of Properties of
the Equation the Equation
1 5+x=6 a+x=b a <b,0 <a,b <10
2 12+x=16 a+x=b a <b,10 <=a,b <=20
3 5+x=3 a+x=b a >b,0 <a,b <10
4 17+x=14 a+x=b a >b,10 <=a,b <=20
5 7-x=8 a-x=b a <b,0 <a,b <10
6 12-x=16 a-x=b a <b,10 <=a,b <=20
7 4-x=1 a-x=b a >b,0 <a,b <10
8 13-x=11 a-x=b a >b,10 <=a,b <=20
9 10+2x=14 b+ax=c c >b, (c-b)/a is +ve integer,
1 <a <=20,0 <b,c <=20
10 19+4x=3 b+ax=c c <b, (c-b)/a is -ve integer,
1 <a <=20,0 <b,c <=20
11 7+6x=8 b+ax=c c >b, (c-b)/a is +ve fraction,
1 <a <=20,0 <b,c <=20
12 11+17x=4 b+ax=c c <b, (c-b)/a is -ve fraction,
1 <a <=20,0 <b,c <=20
13 12-4x=16 b-ax=c c >b, (c-b)/a is +ve integer,
-20 <=a <-1,-20 <=b,c <=20
14 17-10x=7 b-ax=c c <b, (c-b)/a is -ve integer,
-20 <=a <-1,-20 <=b,c <=20
15 3-5x=7 b-ax=c c >b, (c-b)/a is +ve fraction,
-20 <=a <-1,-20 <=b,c <=20
16 19-14x=7 b-ax=c c <b, (c-b)/a is -ve fraction,
-20 <=a <-1,-20 <=b,c <=20
17 12x-15x=19 ax+bx=c -20 <=a,b,c <=20
18 -6x+2x-8=7 ax+bx+c=d -20 <=a,b,c,d <=20
19 -2x-5-5x=-7 ax+bx+c=d -20 <=a,b,c,d <=20
20 11x=-19-13x ax=c+bx -20 <=a,b,c,d <=20
21 15-17x=-11x b+ax=cx -20 <=a,b,c,d <=20
22 -9+12x= 16- 10x b+ax=d+cx -20 <=a,b,c,d <=20
23 (2x+3)/5=1 (ax+b)/c=d 0 <c,d <10, 1 <=a,b <=20
24 (4x-9)/4= 1 (ax-b)/c=d 0 <c,d <10, -20 <=b <-1, 1 <=a <=20
25 (-8+16x)/6=-4 ((a+bx)/c=d -10 <c,d <10, -20 <=a <=20, 1 <=b <=20
26 (-1-14x)/-5= 3 (a-bx)/c=d -10 <c,d <10,
-20 <=b <-1, -20 <=a <=20
27 (-10x+4)/-9=x/2 (ax+b)/c=x/d -10 <c<10, -20 <=d,
1 <=b <=20 , a <=20
28 (-18x-6)/-7=x/11 ((ax-b)/c=x/d -10 <c<10,
-20 <=b <=-1,-20 <=a,d <=20
29 (13x+10)/5=(9x+ 6)/20 (ax+b)/c=(a
2
x+b
2
)/d -10 <=c<=10,
-20 <=a,a
2
,d <=20, 1 <=b,b
2
<=20
30 ((-8x+12)/10=(10x-15)/-2 (ax+b)/c=(a
2
x-b
2
)/d -10 <=c<=10, <=a,a
2
,d <=20,
-20 <= b
2
<=-1,1 <=b,b
2
<=20
31 (-8x-17)/3=(17x-11)/-10 (ax-b)/c=(a
2
x-b
2
)/d -10 <=c<=10,
-20 <=a,a
2
,d <=20, -20 <=b,b
2
<=-1
32 (-13x+19)/-4+(4x+10)/2=-9 (ax+b)/c + (a
2
x+b
2
)/d=f -10 <=c<=10,
-20 <=a,a
2
,d,f <=20, 1 <=b,b
2
<=20
33 (-4x+11)/-3-(15x+8)/4=-1 (ax+b)/c - (a
2
x+b
2
)/d = f -10 <=c<=10,1 <=b,
-20 <=a,d,f <=20,b
2
<=20, -20 <= a
2
<-1
34 (2x-8)/-10+(15x- 8)/10= 5 (ax-b)/c + (a
2
x-b
2
)/d = f -10 <=c<=10, -20 <=d,f <=20,
-20 <=b,b
2
<=-1, 0 <= a,a
2
<20
35 (-4x-16)/4-(5x-9)/8= 3 (ax-b)/c - (a
2
x-b
2
)/d=f -10 <=c<=10, -20 <=d,f <=20,
b
2
<=-1 ,-20 <=b, -20 <= a,a
2
<-1
Figure 8: Difficulty Levels in Equation Guru.
IMPLEMENTATION STRATEGIES FOR “EQUATION GURU” - A User Friendly Intelligent Algebra Tutor
65
