Efﬁcient Interpretation of Large Quantiﬁcations in a

Process Algebra

Beno

ıt Fraikin and Marc Frappier

GRIL, D

epartement d’informatique, Universit

e de Sherbrooke,

2500, Boulevard de l’universit

e, Sherbrooke, Qu

ebec, Canada J1K 2R1

Abstract. The process algebra interpreter EB

PAI supports the EB

method,

which was developed for the purpose of automating the development of infor-

mation systems through code generation and efﬁcient interpretation of abstract

speciﬁcations. For general information system patterns, EB

PAI executes in linear

time with respect to the number of terms and operators in the process expression

and in logarithmic time with respect to the number of entities in the system. This

paper described three optimization techniques of EB

PAI.

1 Introduction

The EB

PAI project is part of the APIS research project [1], whose objective is to de-

velop a case tool that generates executable information systems (IS) from formal spec-

iﬁcations (abstract models). In traditional IS development, the bulk of the design, pro-

gramming and testing is done manually by humans. These three activities consume up

to 70% of the development effort. They are usually not hard to accomplish, but they are

time-consuming and error-prone. The key to reducing development costs and increas-

ing quality clearly resides in eliminating or mechanizing these three tasks. The EB

method was developed for the purpose of automating the development of IS through

code generation and efﬁcient speciﬁcation interpretation. Designed by Frappier and St-

Denis [2], the EB

language includes a process algebra to support an event-oriented

speciﬁcation style. Initial work led to a practical set of rules for an interpreter of EB

process expressions [3], called EB

PAI. This paper describes the last step in efﬁciently

implementing this interpreter.

2 The EB

Speciﬁcation Method

The EB

method [2] has been speciﬁcally created to specify information systems. It

relies on event-oriented speciﬁcation notations like CSP, CCS and LOTOS. However,

special features have been added to take the speciﬁcities of information systems into

account. The input behavior of the system is deﬁned by the process expression main.

Each execution of an action (an input) generates a response (an output). The denota-

tional semantics of EB

is given by a relation R between the traces accepted by main

and the set of output events. A process expression is recursively deﬁned over a set of

Fraikin B. and Frappier M. (2006).

Efﬁcient Interpretation of Large Quantiﬁcations in a Process Algebra.

In Proceedings of the 4th International Workshop on Modelling, Simulation, Veriﬁcation and Validation of Enterprise Information Systems, pages

189-192

DOI: 10.5220/0002500101890192

 SciTePress

symbols Σ, called the action set, λ (an internal action that denotes non-observable ac-

tivity of the system) and  (which denotes a successful termination) in combination

with operators. Operators in EB

draw their inspiration from regular expressions, the

sequential composition (), the choice (|) and the Kleene closure (

∗

), with the addition

of some operators from CSP and LOTOS: synchronization, guard, process call, and

synchronization quantiﬁcation (also called indexing in CSP). The symbol 9 denotes the

interleave operator, i.e., |[∅]| . EB

PAI also have a guard operator and process call. The

symbol PE denotes the set of all process expressions.

It is important to note that quantiﬁcation is a crucial operator in IS speciﬁcation.

This constitutes a major difference from other problem domains where process algebras

are typically used (protocol speciﬁcation for example). Another difference is that EB

is only concerned by trace equivalence. Since the main aim of EB

is to provide an ex-

ecutable speciﬁcation, the speciﬁcation style used to achieve this goal is also different.

Frappier and St.-Denis in [2] have proposed a set of rules that give EB

its operational

behavior. EB

PAI executes a speciﬁcation by simply evaluating the inference rules. We

do not generate code per se; EB

PAI can be considered as a virtual machine and each

speciﬁcation becomes a high-level program. The implementation is the combination of

PAI and the speciﬁcation.

3 Dynamic Optimization in the EB

PAI Interpretation Process

In [3] we provide some static optimizations. However, this is not sufﬁcient to yield

efﬁcient interpretation. To provide a useful tool, we need to optimize other aspects of

the interpretation algorithm, primarily to reduce the time and space complexity for large

quantiﬁcations.

3.1 Optimization of Process Expression Storage in Memory

During an execution, actions and process expressions can be copied several times. Some

execution sequences can require a large amount of memory. The two main causes are

quantiﬁcation and choice resulting in the execution of some non-deterministic speciﬁ-

cations. In order to minimize memory space, process expressions can be represented by

a graph which allows them to be shared. For instance, if E

is a sub-expression of both

and E

, than E

can be instantiated once and referenced by both E

and E

3.2 Optimizing Quantiﬁcation Execution Time: Direct κ-optimization

The EB

language allows the use of quantiﬁcation operators. A basic approach to ex-

ecuting quantiﬁcation operators is too ineffective to be acceptable. To optimize these

executions, we determine by static analysis of each quantiﬁed expression which value

of the quantiﬁed set must be selected based on the parameters of the action to exe-

cute. We call these values κ-values, the positions of the values in the action parameters

κ-positions, and this method direct κ-optimization.

This approach is sufﬁcient to optimize a choice quantiﬁcation, since the quantiﬁca-

tion disappears after the transition. In the case of a quantiﬁed interleave, the quantiﬁca-

tion remains in the result process expression, since it can spawn one interleave process

190

for each value in the quantiﬁcation set. The interleave of the instantiated process ex-

pressions is represented by a function K : T → PE such that K(Π(σ)) is the only

process expression that can execute σ.

3.3 Extending Quantiﬁcation Optimization: Indirect κ-optimization

We have found conditions under which a quantiﬁcation can be optimized when the

algorithm used for the direct κ-optimization fails to ﬁnd a single κ-position for each

action. We can summarize the general idea of indirect κ-optimization, as follows:

During static analysis :

1. Find the quantiﬁed choice operators to deduce the possible functional depen-

dencies (below we refer to choice quantiﬁed variables occurring in the scope

of other quantiﬁcations (interleave or choice) as the dependent variables and

the enclosing quantiﬁed variables as the keys).

2. For all actions not optimized with the algorithm of the κ-optimization: identify

the producer that binds the keys (bId in the example) to the dependent vari-

able (mId in the example) under the condition that the choice and interleave

quantiﬁcations to optimize are synchronized on these actions.

At runtime :

1. When a producer is executed, store the value of the functional dependency

between the set of keys and the dependent variable.

2. Store the value of the new process expression for the operand of the quantiﬁed

interleave in a mapping K, as for direct κ-optimization.

3. When a consumer is executed, delete the stored value of the functional depen-

dency between the keys and the dependent variable.

Complete κ-optimization is not effective for all speciﬁcations that can be written.

Actually, it is not effective for all IS speciﬁcations. However, our aim is to optimize

all speciﬁcations written with the patterns described in [2]. We have established that

the following patterns satisfy the conditions for κ-optimization: the producer-modiﬁer-

consumer, the one-to-many association, the multiple (many-to-many) association, the

n-ary association, the weak entity type, the recursive association, and the inheritance

association.

4 Implementation and Performance

Complexity analysis Let n denote the sum of all |X|, where X is either an entity type

or an association of an EB

speciﬁcation. Let s denote the number of nodes in the tree

representing a process expression, excluding the nodes of a κ-optimized quantiﬁca-

tion (they will be computed with n). Note that for most ISs, s is usually small (e.g.,

s ≪ 10

), whereas n can be quite large (e.g., n ≪ 10

). Figure 1 summarizes the al-

gorithmic and the space complexity of the K-optimization and compares them with no

optimization in EB

PAI and with manual implementation (i.e.. outside EB

PAI). Thus,

for κ-optimizable speciﬁcations, EB

PAI has an overhead of O(s) compared with man-

ual implementation of an IS. With no κ-optimization, the difference is substantial and

PAI becomes impractical as a tool, but it can still be useful for speciﬁcation anima-

tion for validation purposes.

191

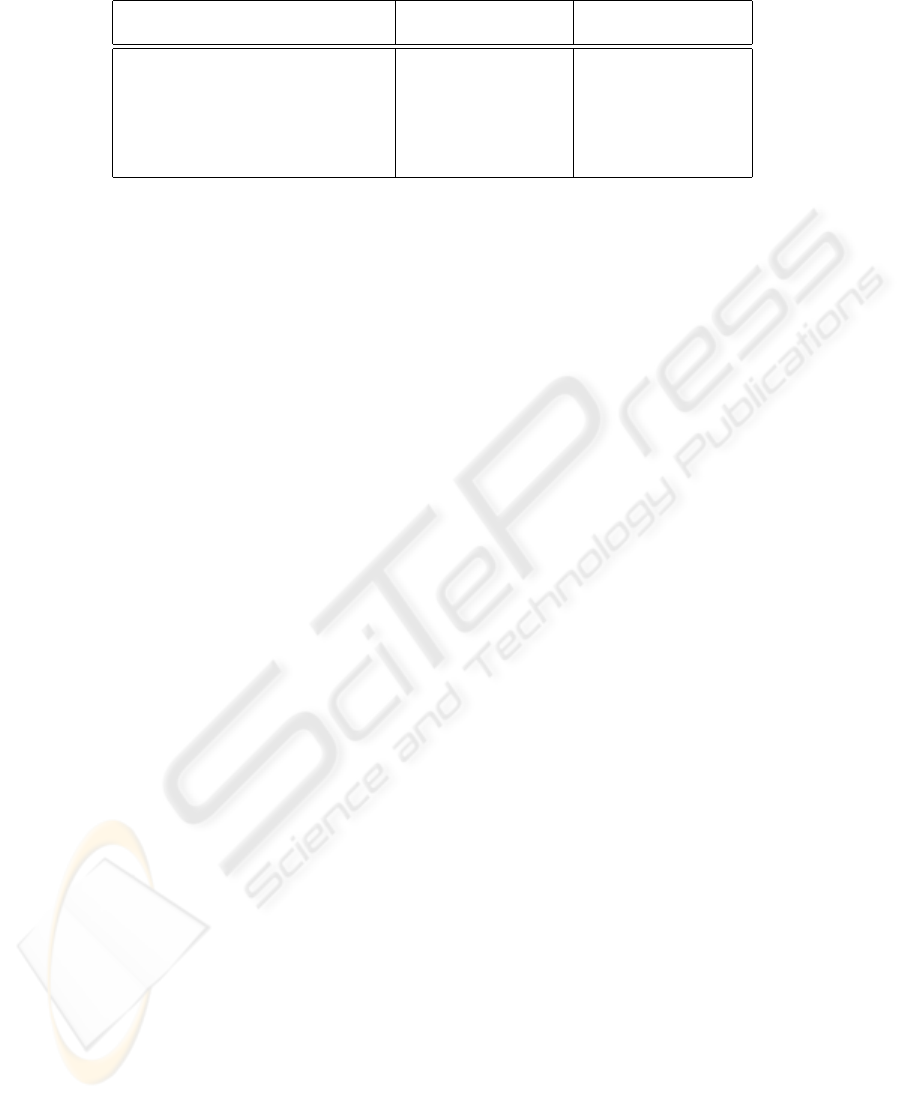
Alg. complexity Space complexity

no optimization O(s.n) O(n + s)

direct κ-optimization O(log(n) + s) O(n + s)

indirect κ-optimization O(log(n) + s) O(n + s)

manual implementation O(log(n)) O(n)

Fig.1: Algorithmic and space complexity of EB

PAI.

Performance for direct κ-optimization Complete κ-optimization is not implemented,

but direct κ-optimization is. The performance for indirect κ-optimization should be

very close to that of direct κ-optimization, because it uses the same data structures

plus an additional hash table to store the functional dependencies. Performance tests

were conduct with a speciﬁcation of a library management system on a Pentium III

800MHz with 384Mo of SDRAM, running GNU/Linux. Indirect κ-optimization has not

been implemented yet; only direct κ-optimization. The transaction mean time of valid

actions is 97ms. Invalid actions (for which the execution failed) are less expensive in

time (approx. 40 ms per action) than valid actions. The same speciﬁcation implemented

in Java using an Oracle database provides an average transaction processing time of

10 ms, which is 10 times faster than EB

PAI. Nevertheless, 100 ms is still acceptable for

many IS systems where the transaction rate is low (e.g., a library management system).

5 Conclusion

In this paper, we have presented two optimization techniques to efﬁciently execute

quantiﬁed process expressions in the EB

process algebra. Their space and algorithmic

complexities are comparable to those of a manual implementation for a large number

of IS speciﬁcations which are determined by a set of speciﬁcation patterns. Direct k-

optimization was implemented in the EB

PAI interpreter. It performs 10 times slower

than a manual implementation of the speciﬁcation for the library system, but its aver-

age response time is acceptable for a large class of IS with low transaction rates, which

demonstrates that abstract interpretation is a viable way of implementing IS.

References

1. Frappier, M., Fraikin, B., Laleau, R., Richard, M.: Automatic production of information sys-

tems. In: AAAI Symposium on Logic-Based Program Synthesis, Stanford University, Stan-

ford, CA (2002)

2. Frappier, M., St-Denis, R.: EB

: an entity-based black-box speciﬁcation method for informa-

tion systems. Software and System Modeling 2 (2003) 134–149

3. Fraikin, B., Frappier, M.: Efﬁcient execution of process expressions using symbolic interpre-

tation. Technical report 8, Universit

e de Sherbrooke, D

epartement d’Informatique, Qu

ebec,

Canada (2005)

192