Test Purpose of Duration Systems
Lotfi Majdoub and Riadh Robbana
Tunisia Polytechnic School
Abstract. The aim of conformance testing is to check whether an implemen-
tation conforms to its specification. We are interested to duration systems, we
consider a specification of duration system that is described by a duration graph.
Duration graphs are an extension of timed systems and are suitable for modeling
the accumulated times spent by computations in the duration systems.
In this paper, we propose a framework to generate automatically test cases accord-
ing to a test purpose for duration graphs. In the first, we define the synchronous
product of the specification and the test purpose of an implementation under test.
In the second, we demonstrate that timed words recognized by the synchronous
product is also recognized by both specification and test purpose. This result al-
lows us to generate tests according to test purpose from the synchronous product.
1 Introduction
Duration systems are an extension of real time systems for which in addition to con-
straints on delays separating certain events that must be satisifed, constraints on accu-
mulated times spent by computation must also be satisfied.
Duration graphs are a formalism used to describe duration systems. They are an
extension of real-time graphs supplied with a finite set of continuous real variables
that can be stopped in some locations (rate=0) and resumed in other locations (rate=1).
These variables are called duration variables.
Duration graphs model some temporal behaviors of real-time systems such as the
accumulated times spent by computations at some particular locations. For instance,
consider a real time scheduler with preemption which handles tasks that can be exe-
cuted in parallel. If one task may be interrupted by other tasks of higher priority, then
the constraint of the execution time of the considered task must be expressed using
the accumulated times. Intuitively, we must use a continuous real variables that can be
stopped when the task is interrupted and resumed when the task is active. Thus, these
systems are modeled with automata supplied with duration variables that count accu-
mulated times spent at some particular control locations.
Our work targets black box conformance testing for duration graphs. Conformance
testing aims to check whether the behavior of some black box implementation conforms
to that of its specification. By ”black box” we mean that the tester has no knowledge
about the implementation, thus can only rely on its observable inputs and outputs. Since,
testing is difficult, expensive, time-consuming and labour-intensive process, moreover,
it should be repeated each time an implementation is modified. A promising approach
Majdoub L. and Robbana R. (2006).
Test Purpose of Duration Systems.
In Proceedings of the 4th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems, pages 67-75
DOI: 10.5220/0002502900670075
Copyright
c
 SciTePress

to improve testing is to automatically generate test cases from formal models of spec-
ification. Using tools to generate test cases automatically may reduce the cost of test
process. However, exhaustive test remains expensive and in some case is impossible.
Springintveld et al in [16] proved that exhaustive testing of deterministic timed au-
tomata with dense time is theoretically possible, but highly infeasible. Some works
define a criteria for selecting test cases to be generated automatically such as coverage
criteria (transition or location coverage of the timed automata)[6,7,10]. Other works try
to define purposes of test and generating test cases according to those purposes[13].
We hope that defining a purpose of test to select test cases converge with the way of
tester reasoning. In practice, and in order to test an implementation the tester specifies
informally some purposes and try to test implementation according to those purposes.
Our contribution is to propose a framework to generate automatically test cases
according to a test purpose for duration graphs. In the first, we present the formalism
used to model specification and test purpose called Duration Variables Timed Graph
with Inputs Outputs (DVTG-IO for short), then we define a synchronous product of both
specification and test purpose which is a duration variables timed graph that combines
specification and test purpose, from this synchronous product we generate test cases
according to the test purpose by applying The algorithm of Tretmans [17].
This paper is organized as follows : In section 1, we present the duration variables
timed graphs with inputs outputs used to model specification. In section 2, we describe
the test purpose. In section 3, we define the synchronous product of specification and
test purpose. the test case is given in section 4.
2 Duration Variables Timed Graphs with Inputs Outputs
(DVTG-IO)
We will introduce in this section formalisms used for describing both specification and
test purpose of implementation under test, called Duration Variables Timed Graph with
Inputs Outputs which are inspired from [15] and that are extensions of the well-known
timed automata defined in [1].
A Duration Variables Timed Graph with Inputs outputs (DVTG-IO for short) is
described by a finite set of locations and a transition relation between these locations.
In addition, the system has a finite set of duration variables that are constant slope
continuous variables, each of them changes continuously with a rate in {0,1}at each
location of the system. Transitions between locations are conditioned by arithmetical
constraints on the values of the duration variables. When a transition is taken, a subset
of duration variables should be reset and an action should be executed, this action can
be either input action, output action or unobservable action (known also as quiescent
[17]).
2.1 DVTG-IO Formal Definition
We consider X a finite set of duration variables. A guard on X is a boolean combi-
nation of constraints of the form x ≺ c where x ∈ X, c ∈ N, ≺∈ {<, ≤, >, ≥}. Let
68

Γ (X) be the set of guards on X. A Duration Variables Timed Graph with Inputs Out-
puts describing a specification is a tuple S = (Q
S
, q
S
0
, E
S
, X
S
, Act
S
, γ
S
, α
S
, δ
S
, ∂
S
)
where Q
S
is a finite set of locations, q
S
0
is the initial location, E
S
⊆ Q
S
× Q
S
is a
finite set of transitions between locations, Act
S
= In ∪ Out ∪ {τ } is a finite set of in-
put actions (designed by a?), output actions (designed by a!) and unobservable action,
γ
S
: E
S
−→ Γ
S
(X
S
) associates to each transition a guard which should be satisfied
by the duration variables whenever the transition is taken, α
S
: E
S
−→ 2
X
S
gives
for each transition the set of duration variables that should be reset when the transition
is taken, δ
S
: E
S
−→ Act
S
gives for each transition the action that should be done
when the transition is taken, ∂
S
: Q
S
× X
S
−→ {0, 1} associates with each loca-
tion q and each duration variable x the rate at which x changes continuously while the
computation is at q.
2.2 State Graph
The semantic of DVTG-IO is defined in terms of a state graph over states of the form
s = (q, ν) where q ∈ Q
S
and ν : X
S
−→ R is a valuation function that assigns a real
value to each duration variables. Let St
S
be the set of states of S. We notice that St
S
is
an infinite set due to the value of duration variables taken on R
+
.
Given a valuation ν and a guard g, we denote by ν |= g the fact that valuation of g
under the valuation ν is true.
We define two families of relation between states :
– Discrete Transition (q, ν)
a
(q
′
, ν
′
) where (q, q
′
) ∈ E
S
, δ
S
(q, q
′
) = a, ν
S
|=
γ(q, q
′
) is true and ν
′
(x) = ν(x) ∀x ∈ X
S
\α
S
(q, q
′
) , ν
′
(x) = 0∀x ∈ α
S
(q, q
′
),
corresponds to moves between locations using transition in E
S
.
– Timed transition (q, ν)
t
(q, ν
′
) such that t ∈ R and ν
′
(x) = ν(x) + ∂(q, x)t
∀x ∈ X
S
, correponds to transitions due to time progress at some location q.
2.3 Example
To illustrate duration variables timed graph with inputs outputs, we give, in figure 1, the
specification of box phone inspired from [13] and described by DVTG-IO. The protocol
is composed by ten locations, transitions between locations and three duration variables
: x,y and z, and it has two phases : authenticity phase and communication phase, we
suppose that authenticity phase does not exceed 5 units of time and communication
phase does not exceed 15 units of time. Duration variables x and y are used respectively
to make constraints on the time of execution of authenticity and communication phases,
z is a timer used to make constraint on the order between actions.
In the initial location ( location 0) implementation wait that the user insert its card
(the input action ?card-in) so it passes to location 1. In location 1, the implementation
verifies the card validity and passes to location 2, if the card is accepted protocol gen-
erates the output !accept and passes to location 3 where the implementation waits that
the user entries its code, if it is correct it passes to location 4 otherwise it remains at
location 3. In location 5, system waits that user composes the number to phone and
passes to locations 7 where it waits the bill and the connection. In locations 7,8 and 9
the user can hang up the connection.
69

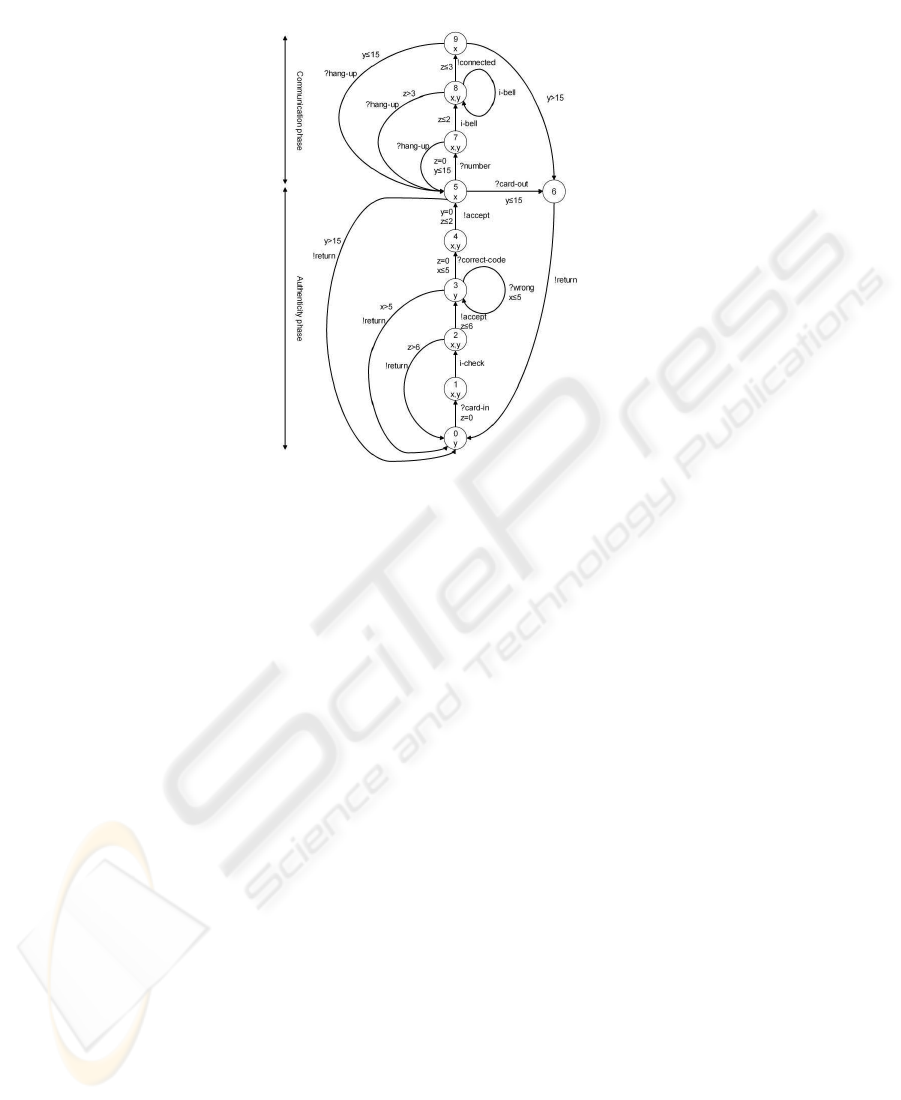
Fig.1. Specification of phone box.
2.4 Computation Sequences, Trails and Timed Words
We define now the notion of computation sequence of a DVTG-IO. These sequences
are defined as finite sequences of configuration. A configuration is a pair (s, τ) where
s is a state and τ is a time value. Intuitively, a computation sequence is a finite path in
the state graph of an extension of S by an observation clock that records the global
elapsed time since the beginning of the computation. Formally, if we extend each
transition relation from states to configuration, then a computation sequence of S is
σ = (s
0
, 0) (s
1
, τ
1
) ... (s
n
, τ
n
).Let CS(S) be the set of computations
sequences of S where s
i
= (q
i
, ν
i
)
The trail corresponding to σ is the sequence ρ = (q
0
, τ
0
) (q
1
, τ
1
) ...
(q
n
, τ
n
)
A timed words is a sequence ω = (a
1
τ
1
a
2
τ
2
...a
n
τ
n
) where a
i
is an action and τ
i
is the valuation of observation clock. Let L(S) be the set of timed words of S
A sequence ω = (a
1
τ
1
a
2
τ
2
...a
n
τ
n
) is considered a timed word of L(M) if and
only if there exists a computation sequence σ = (s
0
, τ
0
) (s
1
, τ
1
) ...
(s
n
, τ
n
) ∈ CS(M) such that a
i
= δ(q
i−1
, q
i
) for i = 1, .., n
3 Test Purpose
Informally, test purpose describes the behavior of the implementation that the tester
has the intention to test. Test purpose allows to select test cases satisfying a specific
70

purpose. We notice that we can define several test purposes for an implementation. We
describe test purpose by a particular duration variables timed graph with inputs outputs
having two particular locations : Accept and Reject. Location Accept defines the verdict
Pass, such that all paths from the initial location to location Accept satisfy the purpose
of test. However, all paths ending at location R eject don’t satisfy the test purpose
A test purpose (TP for short) is a deterministic DVTG-IO ;
T P = (Q
T P
, q
T P
0
, E
T P
, X
T P
, Act
T P
, γ
T P
, α
T P
, δ
T P
, ∂
T P
) where Q
T P
is the
set of locations containing Accept and Reject locations. We suppose that the set Act
T P
= Act
S
this allows to consider that actions of test purpose are also actions of the speci-
fication, and this allows T P to describe the test purpose with the same set of actions as
the specification.
We impose that T P must be complete (∀ q ∈ Q
T P
, ∀ a ∈ Act
T P
, we have
q
a
−→),this hypothesis ensures that the synchronous product of S and T P has the same
behaviors as S. With symbol ”*” we design complementary actions of one action a in
transition of the form q
a
−→
3.1 Example
Figure 2 presents a test purpose of the example presented in figure 1. Informally, the
aim of this test purpose is to test the return of card after more than one communication
such that the total time of communication does not exceed 15 units of time.
The following test purpose is described by a DVTG-IO with five locations {A, B, C,
D, E, } and transitions between locations, we extend this graph by one duration vari-
ables t used to count the accumulation of the durations spent in the communication
phase.
¿From location A, system can pass either to location E(Reject) if the time of com-
munication exceed 15 units of time, we notice that this path does not satisfy the purpose
of test or to location B, In location B, the system wait the input action !connected ( rep-
resenting the fact that there is more than one communication). From location C, system
can return to location A either to establish another communication or to return card dur-
ing 15 units of time, in this case the system passes to location D (Accept) representing
the fact that the purpose is satisfied.
4 Synchronous Product of DVTG-IO
In the previous paragraphs, we have defined graphs describing specification and test
purpose of an implementation under test. In this section, we present the synchronous
product of specification and test purpose.
Intuitively, synchronous product of two graphs describing respectively specification
and test purpose is a duration variables timed graph with inputs outputs such that all
timed words recognized by the synchronous product are recognized by both the speci-
fication and test purpose graphs.
Let S = (Q
S
, q
S
0
, E
S
, X
S
, Act, γ
S
, α
S
, δ
S
, ∂
S
) and
T P = (Q
T P
, q
T P
0
, E
T P
, X
T P
, Act, γ
T P
, α
T P
, δ
T P
, ∂
T P
) be two DVTG-IO’s de-
scribing respectively specification and test purpose of implementation under test and
having the same set of actions (Act).
71

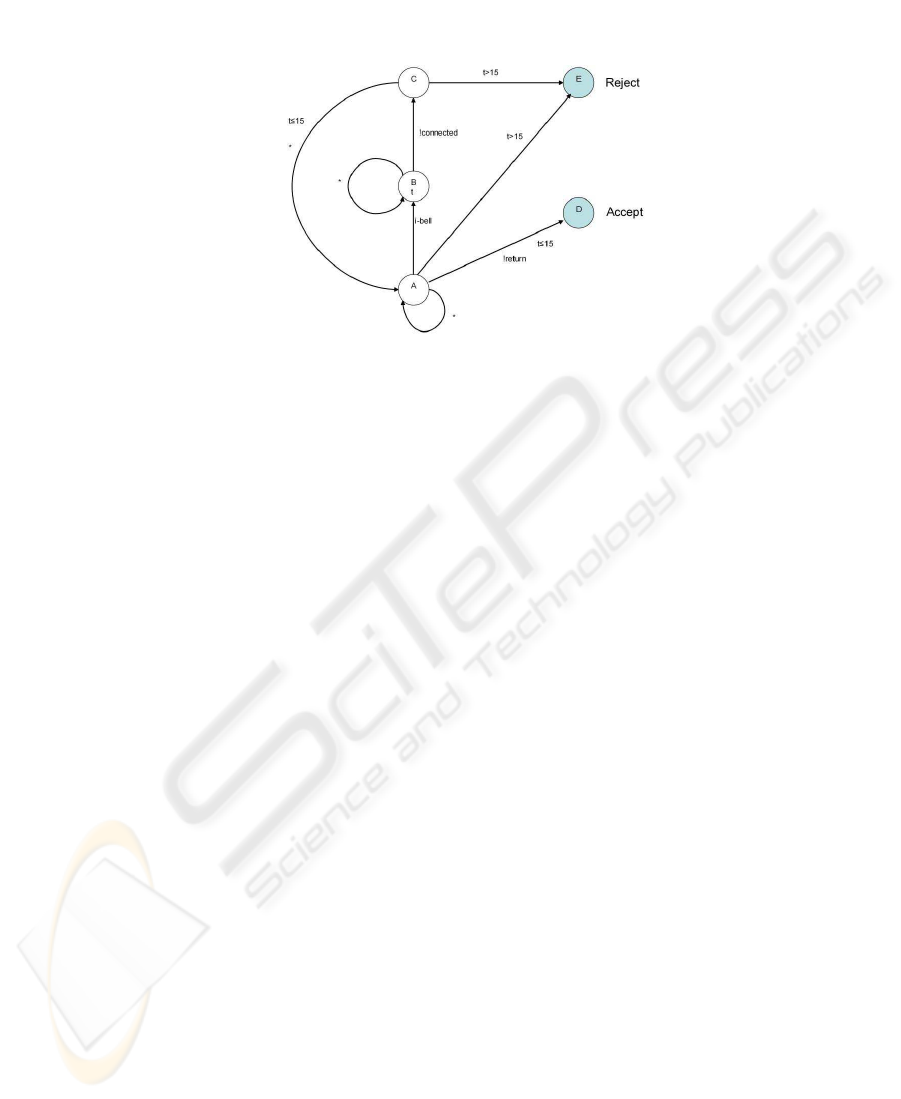
Fig.2. Test purpose.
The synchronous product of S and T P ; M = S ⊗ T P is a DVTG-IO defined by
the tuple :
M = (Q, q
0
, E, X, Act, γ, α, δ, ∂) where
Q ⊆ Q
S
× Q
T P
q
0
= (q
S
0
, q
T P
0
)
E ⊆ Q × Q such that e = ((q
1
, q
2
), (q
′
1
, q
′
2
)) ∈ E iff e
S
= (q
1
, q
′
1
) ∈ E
S
and
e
T P
= (q
2
, q
′
2
) ∈ E
T P
X = X
S
∪ X
T P
γ : E −→ Γ (X) such that γ(e) = γ
S
(e
S
) ∧ γ
T P
(e
T P
)
α : E −→ 2
X
such that α(e) = α
S
(e
S
) ∪ α
T P
(e
T P
)
δ : E −→ Act such that δ(e) = δ
S
(e
S
) = δ
T P
(e
T P
)
∂ : Q × X −→ {0, 1} such that ∂((q
1
, q
2
), x) =

∂
S
(q
1
, x) if x ∈ X
S
∂
T P
(q
2
, x) if x ∈ X
T P
4.1 State Graph for Synchronous Product
A state of synchronous product of DVTG-IO is a pair s = ((q
1
, q
2
), ν) where (q
1
, q
2
) ∈
Q (q
1
∈ Q
S
, q
2
∈ Q
T P
) and ν : X −→ R is a function that assigns a real value to
each duration variables
ν(x) =

ν
S
(x) if x ∈ X
S
ν
T P
(x) if x ∈ X
T P
Let St
M
be the set of states
Two types of transition between states
– Discrete Transition ((q
1
, q
2
), ν)
a
((q
′
1
, q
′
2
), ν
′
) where ((q
1
, q
2
), (q
′
1
, q
′
2
)) ∈ E,
δ((q
1
, q
2
), (q
′
1
, q
′
2
)) = a, ν |= γ((q
1
, q
2
), (q
′
1
, q
′
2
))
72

ν
′
(x) =
ν(x) ∀x ∈ X\α((q
1
, q
2
), (q
′
1
, q
′
2
))
0 ∀x ∈ α ((q
1
, q
2
), (q
′
1
, q
′
2
))
– Timed transition ((q
1
, q
2
), ν)
t
((q
1
, q
2
), ν
′
) where t ∈ R
+
, ν
′
(x) = ν(x) +
∂((q
1
, q
2
), x)t ∀x ∈ X
Let (S
M
, ) the state graph of M
4.2 Example
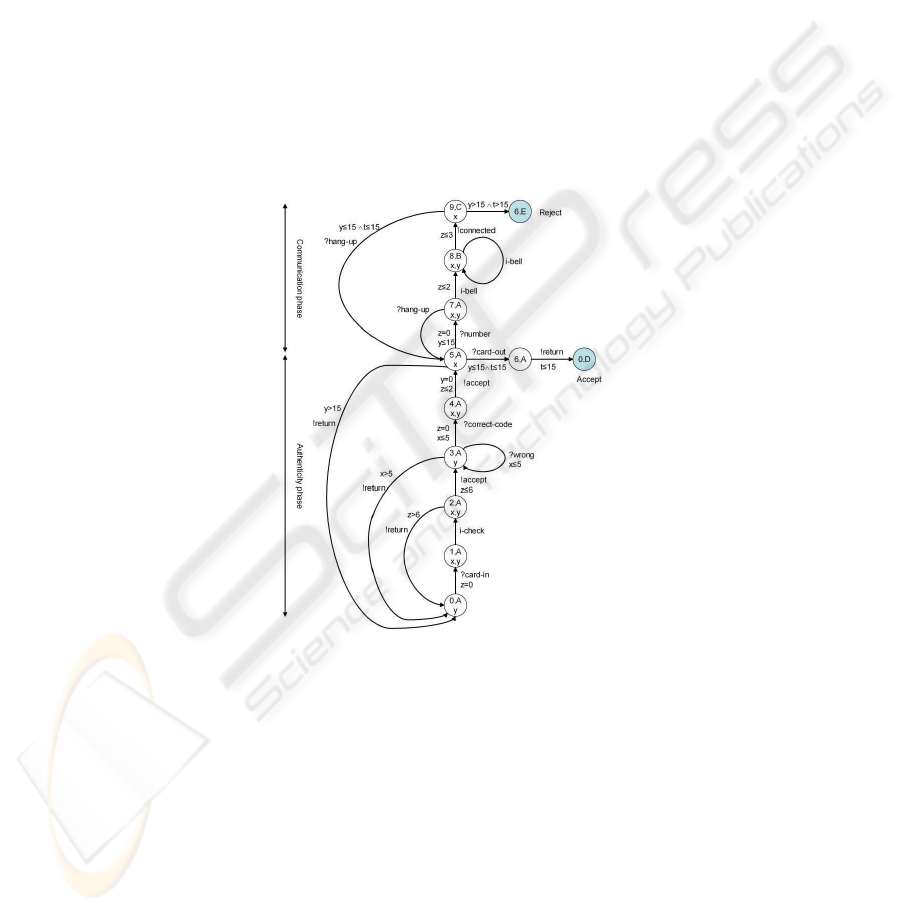
The example of figure 3 describes the synchronous product of the previous specification
and test purpose presented in figure 1 and 2
Fig.3. The synchronous product specification test purpose.
Now, we present the theorem that demonstrates that all timed words recognized by
M are also recognized by both S and T P
Theorem
Let M
1
and M
2
two DVTG-IO’s, M = M
1
⊗ M
2
the synchronous product
We have
L(M) = L(M
1
) ∩ L(M
2
)
73

Proof
Demonstrating that L(M) = L(M
1
) ∩ L(M
2
) consists to demonstrate that ∀ω ∈
L(M)
?
⇐⇒ ω ∈ L(M
1
) and ω ∈ L(M
2
)
Let ω be a timed word of L(M ) , ω = a
1
τ
1
a
2
τ
2
...a
n
τ
n
where a
i
∈ Act , τ
i
∈
R
+
for i = 1..n
⇐⇒ ∃σ = ((q
01
, q
02
), ν
0
, 0) ((q
11
, q
12
), ν
1
, τ
1
) ... ((q
n1
, q
n2
), ν
n
, τ
n
) ∈
CS(M )
and δ((q
i−11
, q
i−12
)(q
i1
, q
i2
)) = a
i
∀i = 1..n
⇐⇒ ∀i = 1..n ((q
i−11
, q
i−12
), ν
i−1
) ((q
i1
, q
i2
), ν
i
) is a transition of (S
M
, )
and δ((q
i−11
, q
i−12
)(q
i1
, q
i2
)) = a
i
∀i = 1..n
⇐⇒ ∀i = 1..n
(q
i−11
, ν
i−11
) (q
i1
ν
i1
) is a transition of (S
M
1
, )
(q
i−12
, ν
i−12
) (q
i2
, ν
i2
) is a transition of (S
M
2
, )
and δ(q
i−11
, q
i1
) = δ(q
i−12
, q
i2
) = a
i
∀i = 1..n
⇐⇒ (q
01
, ν
01
, 0) (q
11
, ν
11
, τ
1
) ... (q
n1
, ν
n1
, τ
n
) ∈ CS(M
1
)
(q
02
, ν
02
, 0) (q
12
, ν
12
, τ
1
) ... (q
n2
, ν
n2
, τ
n
) ∈ CS(M
2
)
and δ(q
i−11
, q
i1
) = δ(q
i−12
, q
i2
) = a
i
∀i = 1..n
⇐⇒ a
1
τ
1
a
2
τ
2
...a
n
τ
n
∈ L(M
1
) and a
1
τ
1
a
2
τ
2
...a
n
τ
n
∈ L(M
2
)
This theorem is important because it allows us to generate test cases from specifi-
cation and satisfying a test purpose. So, we generate test cases from the synchronous
product of specification and test purpose.
5 Test Generation
In order to generate test cases that satisfies a test purpose, and thanks to the above the-
orem, we suggest to generate test cases from the synchronous product of specification
and test purpose. We adapt the untimed test generation algorithm of Tretmans [17] to
our context. The algorithm builds a test case in the form of tree duration variables timed
graph with inputs outputs such that leaves of the tree represent the verdict of the test
: pass or fail. If the test leads to leaf pass is considered conform to its specification,
otherwise is considered not conform. In every location of the tree, the tester select the
transition to be taken depending on the guard and the action assigned, it can either wait
the emission by the implementation of an output or insert an input action and respecting
the guard of transition. We notice that the graph representing test is not synchronous. In
the sense, that an input action not imperatively succeeded by an output action.
6 Conclusion
We have presented in this paper our framework for generating test cases according to
test purpose for duration variables timed graph with inputs outputs.. We have described
the specification and the test purpose of an implementation under test by a duration vari-
ables timed graphs, and we have defined the synchronous product of the specification
74

and test purpose. Finally, we have demonstrated that all timed words recognized by the
synchronous product are recognized by both the specification and test purpose. Thanks
to this result, we can generate test cases according to a test purpose.
Regarding future work, we notice that in this paper, we don’t treat the problem of
the infinity of the state space, due to the infinite number of duration variables values,
we can solve this problem by adapting the region graph approach or by approximation.
References
1. R.Alur and D.Dill, A Theory of Timed Automata, Theoretical Computer Science, 126 : 183-
235, 1994
2. A.Bouajjani, Y.Lakhnech, R.Robbana, From Duration Calculus to Linear Hybrid Systems,
In Proc. Computer Aided Verification (CAV’95), Liege Belgium, 1995
3. F.Cassez, K.G Larsen, The Impressive Power of Stopwatches, In Proc. Conference on Con-
currency Theory (CONCUR’00), Penssylvania, USA, 2000
4. A.En-Nouaary, R.Dssouli, F.Khender, and A.Elqortobi, Timed Test cases generation based
on state characterisation technique, In RTSS’98. IEEE, 1998
5. T.Henzinger, Z.Manna, and A.Pnuelli, What good are digital clocks?, In ICALP’92, LNCS
623, 1992
6. A.Hessel, K.G. Larsen, B.Nielsen, P.Pettersson and A.Skou, Time-optimal Real-Time Test
Case Genereation using UPPAAL, In Proceding of third International Workshop on Formal
Approaches to Testing of Software, FATES’03, 2003
7. A.Hessel, P.Pettersson, A Test Case Generation Algorithm for Real-Time Systems, In Proced-
ing of 4th international Conference on Quality software QSIC’04 pages 268-273, 2004
8. A.Khoumsi, A Method for Testing the Conformance of Real Time Systems, IEEE Interna-
tional Symposium on formal Techniques in Real-Time and Fault tolerant Systems, FTRTFT
volume 2469 of LNCS Springer Verlag, September 2002.
9. A.Khoumsi, T.Jeron, and H.Marchand, Test Cases Generation for Nondeterministic Real-
time Systems, In FATES’03, 2003
10. M.Krichen, S.Tripakis, Black-Box Conformance Testing for Real-Time Systems, SPIN’04
Workshop on Model Checking Software, 2004
11. D.Lee, M.Yannakakis, Principles and Methods of Testing Finite State Machines, Proceedings
of the IEEE, 84 : 1099-1123, August 1996
12. L.Majdoub and R.Robbana, Verificaton of Duration Systems with one Preemption,
ACS/IEEE International Conference on Computer Systems and Applications, Tunisia 2003
13. P.Morel, Une algorithmique efficace pour la g
´
en
´
eration automatique de tests de conformit
´
e,
these of Rennes University, 2000
14. R.Robbana, Sp
´
ecification et V
´
erification des Syst
`
emes Hybrides, These, Joseph Fourier Uni-
versity Grenoble, October 1995
15. R.Robbana, Verification of Duration Systems using an Approximation Approach, Journal of
Computer Science and Technology, Vol 18, No2, pp. 153-162, March 2003
16. J.Springintveld, F.Vaandrager, and P.D’Argenio, Testing Timed Automata, Theoretcal Com-
puter Science, 254, 2001
17. J.Tretmans, Testing Concurrent Systems : A Formal Approach, CONCUR’99 , 10th Int, con-
ference on Concurrency Theory, volume 1664 of Lecture Notes in Computer Science, pages
46-65, Springer -Verlag, 1999
75