MATHEMATICAL FRAMEWORK FOR

GENERALIZATION AND INSTANTIATION OF KNOWLEDGE

Marek Reformat

thinkS

: thinking Software and System laboratory

Electrical and Computer Engineering, University of Alberta

ECERF Building W6-023, 9107-116 Street, Edmonton, Alberta, Canada, T6G 2V4

Keywords:

Knowledge representation, protoforms, instances, category theory, ﬁbration, abstract data types.

Abstract:

Templates, patterns, and blueprints are constructs that humans use to represent highly abstract knowledge.

Quality of such processes as reasoning, speaking, running, and driving depends on people’s abilities to process

these constructs. Recently, they have been named protoforms. On the other hand, concrete pieces of knowledge

can be seen as instances of the protoforms.

A very important task is to ﬁnd mechanisms that will be able to organize and control protoforms and their

instances. They would provide methods for deﬁning properties of protoforms and their instances, describing

their interactions, and controling ways how they can be merged. The paper describes a concept of applying

category theory to describe protoforms and their instances in a more formal way.

1 INTRODUCTION

The fundamental goal of knowledge representation

is to prepare an environment suitable for performing

analysis and processing of represented knowledge.

Zadeh’s (Zadeh, 2002) observation is that humans use

patterns representing different aspects of everyday ac-

tivities, such as building sentences, and making de-

cisions. To generalize this observation, Zadeh intro-

duced the concept of protoforms (prototypical forms).

They represent a wide range of concepts, procedures,

and schemes related to different activities.

At the time when protoforms represent a general-

ized knowledge, a speciﬁc pieces of knowledge are

instances of protoforms. A single protoform together

with its instances can be related to other protoform

and their instances. In general we can talk about a net-

work of ”relations” among different protoforms and

instances.

Category theory (Barr and Wells, 1999) is a disci-

pline of mathematics dedicated to the theory of struc-

tures – it deals with structures and relationships be-

tween them in an abstract way. The basic elements of

category theory are objects and morphisms (arrows).

Category theory focuses on relations that exist among

objects, it tries to describe objects via their interac-

tions with an environment and among themselves.

In the paper, a mathematical scheme for analysis

and inference about protoforms and their instances is

described. The categories Protoforms and Instances

are deﬁned. Each object of the category Protoforms

is a single protoform represented as an algebraic sig-

nature containing a set of types, and a set of opera-

tions over those types. In this category, morphisms

are ”relations” that translate the vocabulary (types)

and operations of one signature (protoform) into the

vocabulary and operations of another. Objects of the

category Instances are instances (individuals) build

on protoforms. Relations among objects of both cat-

egories, i.e., Protoforms and Instances, are deﬁned

by special relations called ﬁbrations. This means that

instances are ﬁbers built over protoforms.

2 PROTOFORMS

The concept of protoforms, introduced by Zadeh in

(Zadeh, 2002), represents an interesting idea of gener-

alization. A protoform – a short of prototype form – is

deﬁned as ”an abstracted summary”. The protoform

is a symbolic expression deﬁning a construct - a con-

cept, proposition, command, question, scenario, case,

249

Reformat M. (2007).

MATHEMATICAL FRAMEWORK FOR GENERALIZATION AND INSTANTIATION OF KNOWLEDGE.

In Proceedings of the Second International Conference on Software and Data Technologies - PL/DPS/KE/WsMUSE, pages 249-254

DOI: 10.5220/0001344802490254

 SciTePress

or a system of such constructs. It has been already

shown that protoforms have a universal character, and

are useful for building intelligent systems (Kacprzyk

and Zadrozny, 2005) (Yager, 2006).

Example: One of the simplest protoforms are con-

cepts. A concept car is such an example. This proto-

form identiﬁes components of a car, and ”relations”

between them. There are many concepts related to

car, for example racing car, sport utility car, and all

of them constitute a network of concepts.

Example: Another portoform can be a single propo-

sition V is B, where V is a variable, and B is a subset

indicating the allowable values for the variable. This

protoform can be a building block of more complex

protoforms (Yager, 2006).

Example: Protoforms can be also used to represent

database query summaries (Kacprzyk and Zadrozny,

2005). In this case, a query summary such as Most

records meeting conditions B match query S can be

represented by a profotorm: Most BRs are S, where

R means records, B is a ﬁlter, and S is a query. Ev-

idently, as protoforms may form a hierarchy, higher

level (more abstract) protoforms can be deﬁned, for

instance replacing most by a general linguistic quan-

tiﬁer Q: QBRs are S.

3 CATEGORY THEORY

3.1 Basics of Category Theory

Category theory (Barr and Wells, 1999) is a branch

of mathematics that deals with structures and rela-

tionships among them. The structures are called ob-

jects and a relationship between two objects is called

a morphism. The essence of category theory, as stated

in (Fiadeiro, 2005), is that category theory character-

izes objects in terms of their ”social life”. This so-

cial life represents interaction of objects among them-

selves and their universe (environment).

Due to the space limitation we do not provide def-

initions of basic concepts of category theory, such as

category, morphism, functor, and universal construc-

tions (for example, pushouts). Deﬁnitions of these

concepts can be found in any category theory book,

for example (Jacobs, 2001).

3.2 Fibrations

Special types of functors, that deﬁne relationships

that exists among objects that belong to two differ-

ent categories, are called ﬁbrations (Barr and Wells,

1999). A ﬁbration is designed to capture collections

−1

(i) ϕ

−1

( j)

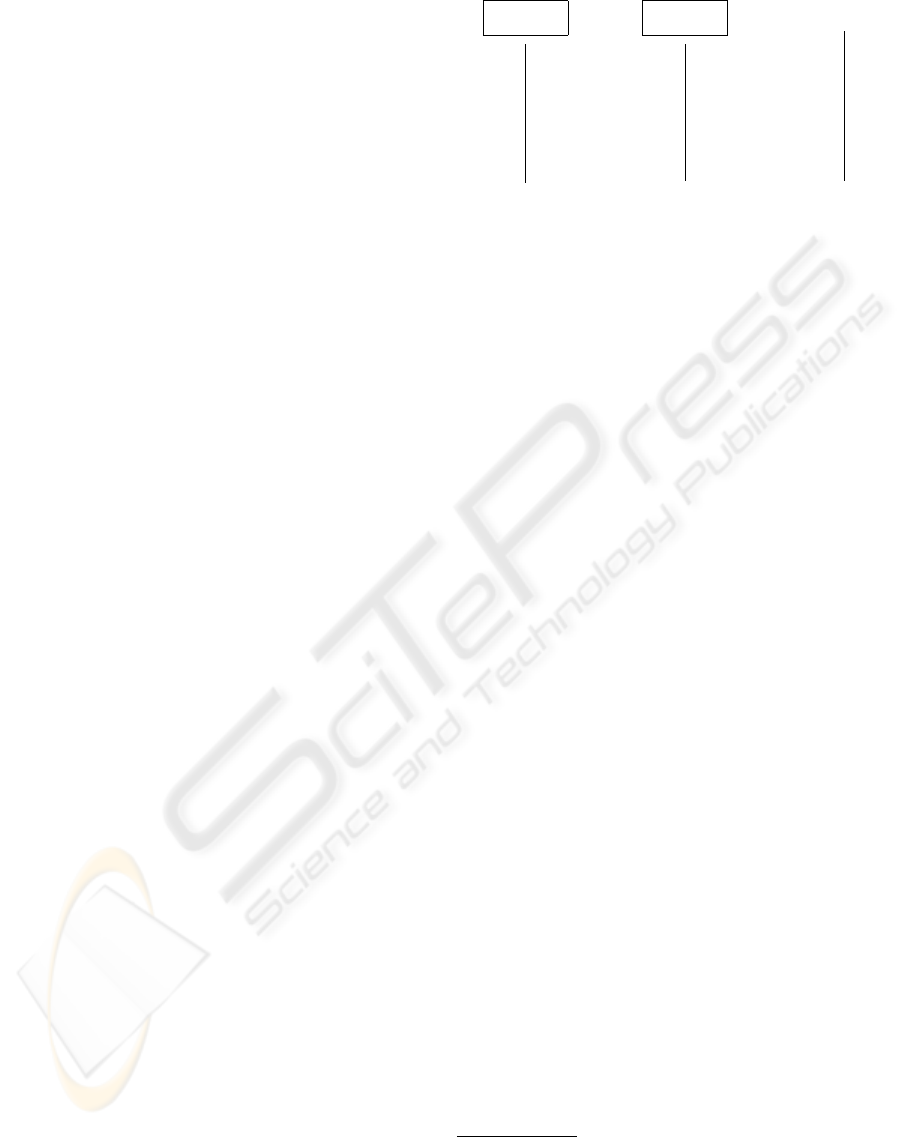
Figure 1: Fibers over i and j (each box represents a set of

objects X that are mapped into i and j respectively.

of categories varying over a base category. An exam-

ple can be collections of sets (X

)

i∈I

varying over a

base, or index, set I, Fig. 1. Let’s consider a functor

ϕ : X → I . The sets in the category X appear as

ﬁbers over elements/objects of category I

−1

(i) = {x ∈ X|ϕ(x) = i}

for each i ∈ I . In other words, a ﬁber is a collec-

tion of items of one category that can be mapped (via

ﬁbration) into a single element (object) of another cat-

egory.

A formal deﬁnition of ﬁbration is based on the

concept of cartesian morphisms

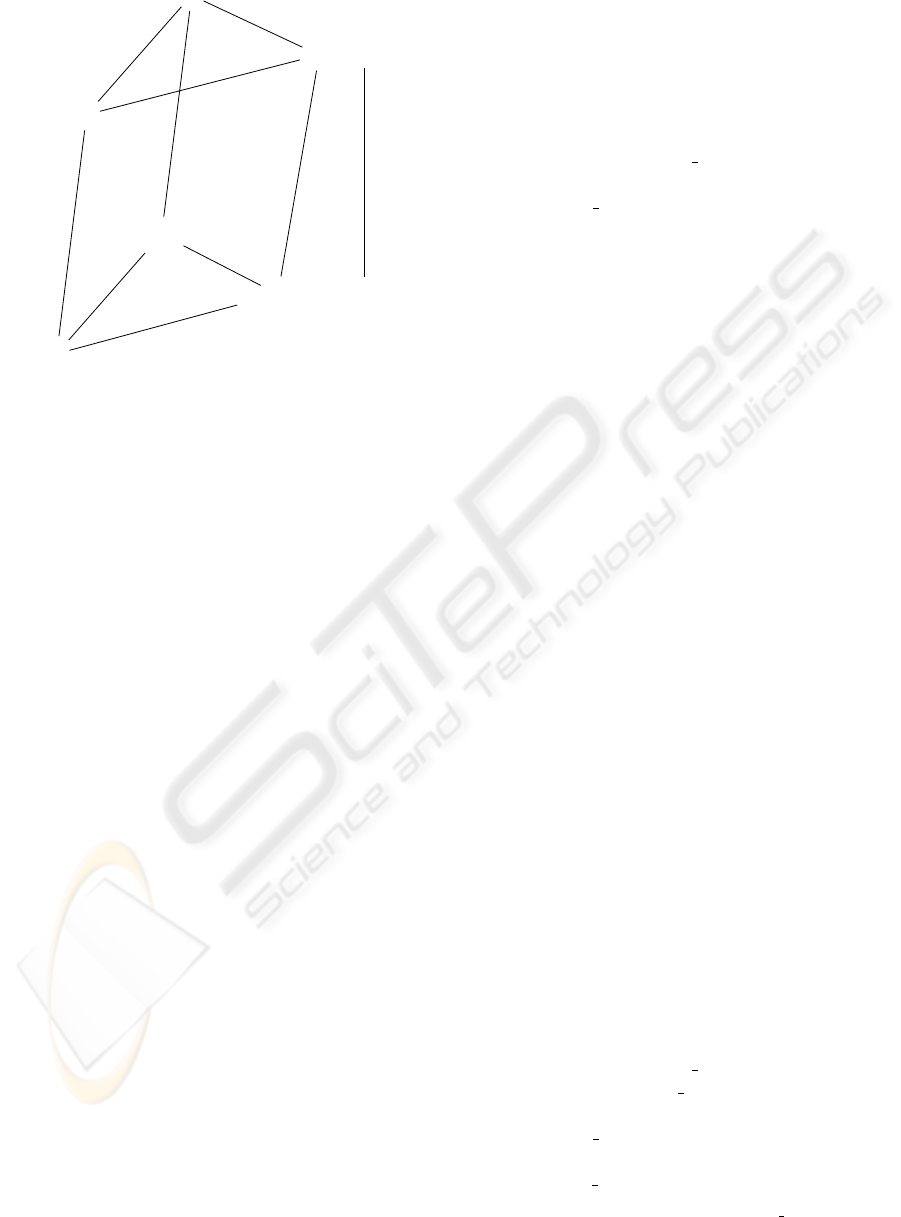
Deﬁnition 1 Let P : E → C be a functor between

categories, let f : C → D be an arrow of C , and let

P(Y) = D. An arrow u : X → Y of E is cartesian for

f and Y if (see Fig. 2 for a graphical representation):

• P(u) = f

• for any arrow v : Z → Y of E and any arrow h :

P(Z) → C of C for which f ◦ h = P(v), there is a

unique w : Z → X in E for which u ◦ w = v and

P(w) = h.

Deﬁnition 2 A functor P : E → C is a ﬁbration if

there is a cartesian arrow for every f : C → D in C

and every object Y in E for which P(Y) = D.

If P : E → C is a ﬁbration, one also says that E is

ﬁbered over C . In that case, C is the base category

and E is the total category of the ﬁbration. Some

authors represent a ﬁbration vertically:

↓

This way of representing a ﬁbration is very intuitive.

There is also a dual concept to ﬁbration called coﬁbra-

tion or opﬁbration. We skip the formal deﬁnition of opﬁ-

bration, but elements of opcartesian (dual to cartesian) mor-

phism are used in Section 7 to illustrate beneﬁts of the ap-

proach we proposed in the paper.

ICSOFT 2007 - International Conference on Software and Data Technologies

250



P(Z)



P(Y)=D



P(v)



h = P(w)

Figure 2: Formal deﬁnition of a ﬁbration (objects X, Y, Z are

of E , and C, P(Z), P(Y)=D of C ).

4 ALGEBRAIC

REPRESENTATION

4.1 Abstract Data Types and Signatures

An abstract data type (ADT) is a mathematical speci-

ﬁcation of data and operations that can be performed

on the data. An ADT is created by identifying types

of data that become its elements, and providing in-

formation about operations that can be performed on

these identiﬁed types of data. The only information

is a name of operation, its domain and co-domain.

The actual implementation, i.e., values of the identi-

ﬁed types and the results of operations on these values

are not deﬁned.

The technique of algebraic speciﬁcation of ab-

stract data types can be introduced informally by

deﬁning the concept of signature, called also an al-

gebraic signature. The signature deﬁnes types of data

that are used by the abstract data type, and a set of

operations. Its formal deﬁnition is shown below.

Deﬁnition 3 A signature SIG = (T, OP) consists

• T, the set of types (also called sorts);

• OP, the set of constant and operation symbols; K

is a set of constant symbols of types t ∈ T, OP

w,t

is a set of operation symbols with argument types

w ∈ T

∗

is a set of strings built using types t ∈

T, i.e., ht

, ..., t

i), and a range type t ∈ T (t

n+1

∈

T).

An intuitive data type: boolean can be deﬁned us-

ing ADT. Its signature is the following:

bool =

sort bool

opns: TRUE, FALSE → bool

NOT: bool → bool

AND: bool bool → bool

engine =

sort piston, valve, engine

block, engine

opns eASSEMBLY: piston × valve

× engine block, → engine

Figure 3: Signature of a concept engine.

where T = {bool}, and K

= {TRUE, FALSE},

w,t

= {NOT, AND}. As it can be seen, there is no

information about the values boolean can take, as well

as results of operations AND and NOT.

4.2 Protoforms as Algebraic Signatures

High level of abstraction and universal character of

both protoforms and ADT have led us to the idea of

applying algebraic signatures for representing proto-

forms. The very aspects of ADT, such as focus on

generic nature of relationships among data compo-

nents and an implementation independence, make this

idea very attractive.

Let us take a look at a simple example of a proto-

form signature. The protoform signature presented in

Fig. 3 is the signature of a simple concept engine. It

contains a number of components and a single func-

tion identifying a relation between them.

The signature engine can be treated as an ele-

mentary protoform, and other protoforms can be built

based on it. For example, it can be extended by in-

troducing new types and operations. The extended

signature is shown in Fig. 4.

The signature engine can also be used as a part of

more complex signatures. An example of such signa-

ture is presented in Fig. 5. This signature named car

contains additional types and operations.

turboEngine =

sort piston, valve, engine

block, engine,

turbocharger, turbo

engine

opns eASSEMBLY: piston × valve

× engine

block, → engine

tASSEMBLY: engine × turbocharger

→ turbo engine

Figure 4: Signature of a concept turbo

engine.

MATHEMATICAL FRAMEWORK FOR GENERALIZATION AND INSTANTIATION OF KNOWLEDGE

251

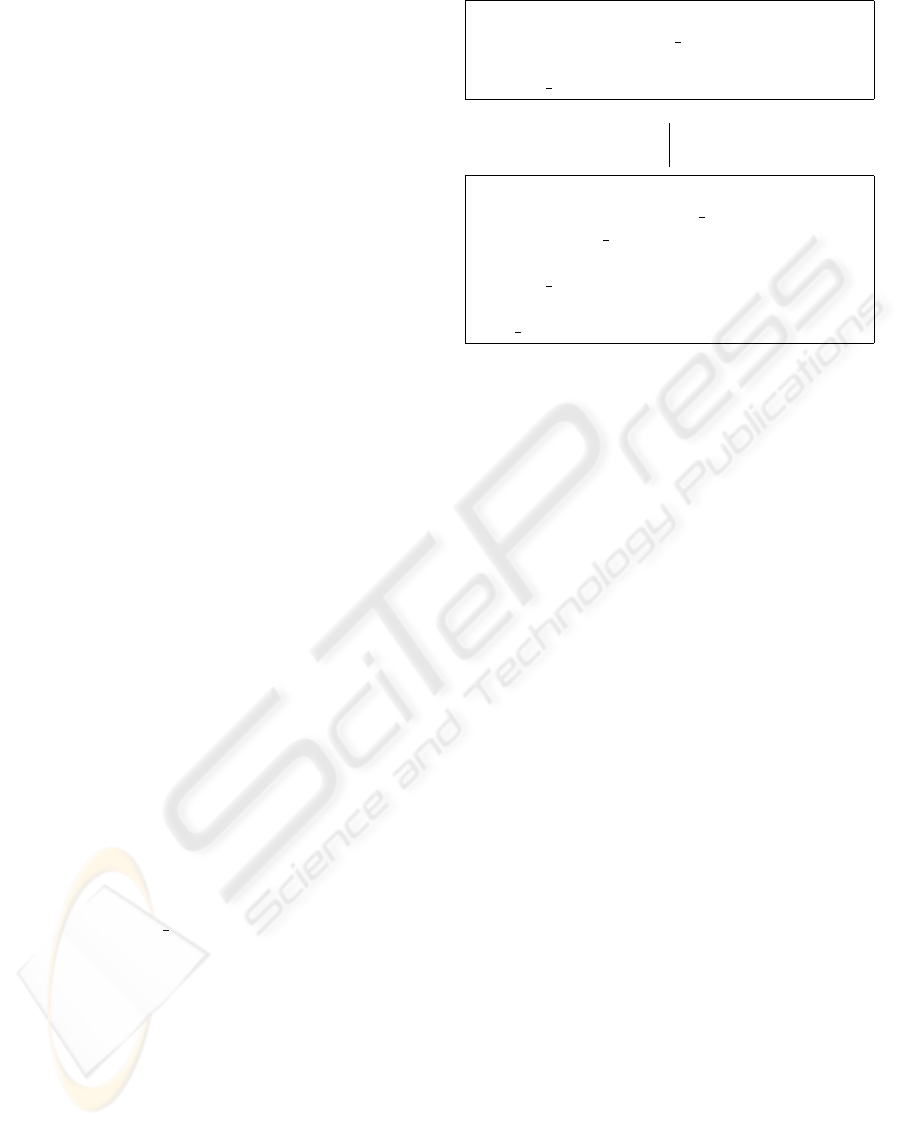
car =

sort engine, body, interior, wheel, car

opns cASSEMBLY: engine × body

× interior × wheel → car

Figure 5: Signature of a concept car.

5 PROTOFORMS AND

CATEGORY THEORY

5.1 Concept

Representation of protoforms using algebraic speciﬁ-

cations (signatures), presented in the Section 4.2, cre-

ates a possibility of formalizing protoforms and pro-

cesses of their construction. Therefore, we deﬁne a

category Protoforms in the following way.

Deﬁnition 4 The category Protoforms has

objects

protoforms represented by signatures

morphisms

signature morphisms – it maps the sorts and oper-

ations from one signature to another (possible mor-

phisms are substitutions, inclusions, extensions).

Construction of category Protoforms provides

several advantages: a more mathematical approach to

dealing with protoforms, a better understanding of re-

lations between protoforms, a systematic approach to

constructing more complex protoforms.

The category Protoforms is presented here in the

form of examples of their objects, and an example of

application of the pushout construction.

5.2 Protoforms as Objects

The signatures presented in Fig. 3, 4, and 5 are ob-

jects of the category Protoform. It can be shown that

there is a very simple morphism between two of them,

Fig. 6. This morphism is just an extension of the

sort engine into turbo

engine. The protoform turbo-

Engine contains an additional type turbocharger and

one more operation tASSAMBLY that represents a pro-

cess of adding turbocharger to an engine.

For the purpose of the next subsection related

to construction of more complex protoforms, these

protoforms are redeﬁned, Fig. 7, and the signature

car is renamed protoformCar.

5.3 Protoform Category and Universal

Constructs

Universal constructions can be used to deﬁne relation-

ships among protoforms.

engine

sort piston, valve, engine

block, engine

opns eASSEMBLY: piston × valve

× engine block → engine

turboEngine

sort piston, valve, engine

block, engine, tur-

bocharger, turbo

engine

opns: eASSEMBLY: piston × valve

× engine block → engine

tASSEMBLY: engine × turbocharger →

turbo

engine

Figure 6: An example of a morphism in the category Proto-

forms.

protoformEngine =

sort engine

protoformTurboEngine =

sort turboEngine

Figure 7: Objects of Protoform. category

Example A pushout that uses protoformTurboEngine

and protoformCar to create a new protoform - proto-

formTurboCar is shown in Fig. 8. The process of con-

structing a new protoform is ”deﬁned” by the map-

pings of the sort engine of protoformEngine to the sort

engine of protoformCar, and to the sort turboEngine

of protoformTurboEngine. The engine and turbo-

Engine are ”amalgamated”, and the resulting proto-

form has the sort turboEngine.

6 INSTANTIATION AND

CATEGORY THEORY

6.1 Models

The deﬁnition of signature (Section 4.1) identiﬁes

sorts (types) and operations, but does not provide any

details about them, i.e., values and relations among

these values. However, each signature can be used to

create a model (an algebra). This is done by assigning

concrete values to each type and operation.

Deﬁnition 5 A model or algebra for a signature SIG

consists of a T-indexed collection (A

)

t∈T

of carrier

sets together with a collection of suitably typed op-

erations: each operation symbol OP : t

, ..., t

→ t

n+1

ICSOFT 2007 - International Conference on Software and Data Technologies

252

protoformEngine

sort engine

protoformTurboEngine

sort turboEngine

protoformCar

sort engine, body, interior, wheel, car

opns cASSEMBLY: engine × body × interior ×

wheel → car

protoformTurboCar

sort, turboEngine, body, turbo

car

opns tASSEMBLY: turboEngine × body →

turbo

car

Figure 8: An example of a pushout (PO) in the category Protoforms.

in SIG is mapped to an actual operation JOPK : A

... × A

→ A

n+1

between the corresponding carrier

sets. Thus a model consists of a pair ((A

)

t∈T

, J

K).

In other words a model represents a ”concrete”

piece of knowledge built based on a signature. A sin-

gle signature can be used to create several models.

Example. A simple model (each type has only one

possible value) that can be built based on engine is

presented below.

engine

piston

: {3− ring

pistons}

valves

: {intake

and exhaust valves}

engine

block

: {block

without sparks}

engine

: {diesel

engine}

JeASSEMBLY

K: A

piston

× A

valves

× A

engine

block

→ A

engine

(3− ring

pistons,

intake

and exhaust valves,

block

without sparks) → diesel engine

From the perspective of category theory models

built based on signatures can be treated a category.

Deﬁnition 6 The category Sig-Model of models of

signatures has

objects

(SIG, (A

, J

K) where (A

, J K) is a model for SIG

morphisms

(φ, (H

)) : (SIG, (A

, J K) → (SIG

′

, (A

′

, J K

′

)

where each morphism consists of a morphism of sig-

nature φ : SIG → SIG

′

, and a |SIG|-indexed collection

of operations

A relationship between signatures and models re-

sembles the relationship between protoforms and in-

stances. In order to utilize this relationship, we need

to build a category of instances.

Deﬁnition 7 The category Instances has

objects

models of protoform signatures

morphisms

model morphisms containing signature morphims

6.2 Instantiation and Fibers

The concept of a ﬁbration (Section 3.2) represents a

very interesting way of formalizing relations between

two categories. It has been found (Jacobs, 2001) that

the relationship between a set of models and a sin-

gle signature is a ﬁbration. So the functor between

the category of models Sig

Model and the category of

signatures Sig is a ﬁbration. This can be represented

in the following way:

Sig-Model

↓

Sig

In other words the functor Sig

Model → Sig

sends models to its underlying signature. A ﬁber over

an object (signature) SIG ∈ Sig is a model of the sig-

nature SIG. We can induce that similar relation ex-

ists between objects of the categories Instances and

Protoforms.

Instances

↓

Protoforms

This deﬁnes and formalizes relationships that exist

between protoforms and instances. All these observa-

tions can be summed-up into a single statement that

instances are ﬁbers over protoforms.

7 DISCUSSION

The idea of treating protoforms as a base category

for instances brings a very elegant way of identify-

ing relationships that exist among protoforms and in-

stances. Fig. 9 represents a very simple knowledge

system that will be used to explain beneﬁts of the

idea we propose in the paper. The system contains

three protoforms engine, turbo

engine, and car turbo.

Each of the protoform signatures is a base for a set

of models – instances. Instances of engine are rep-

resented by small circles with two explicit instances

MATHEMATICAL FRAMEWORK FOR GENERALIZATION AND INSTANTIATION OF KNOWLEDGE

253

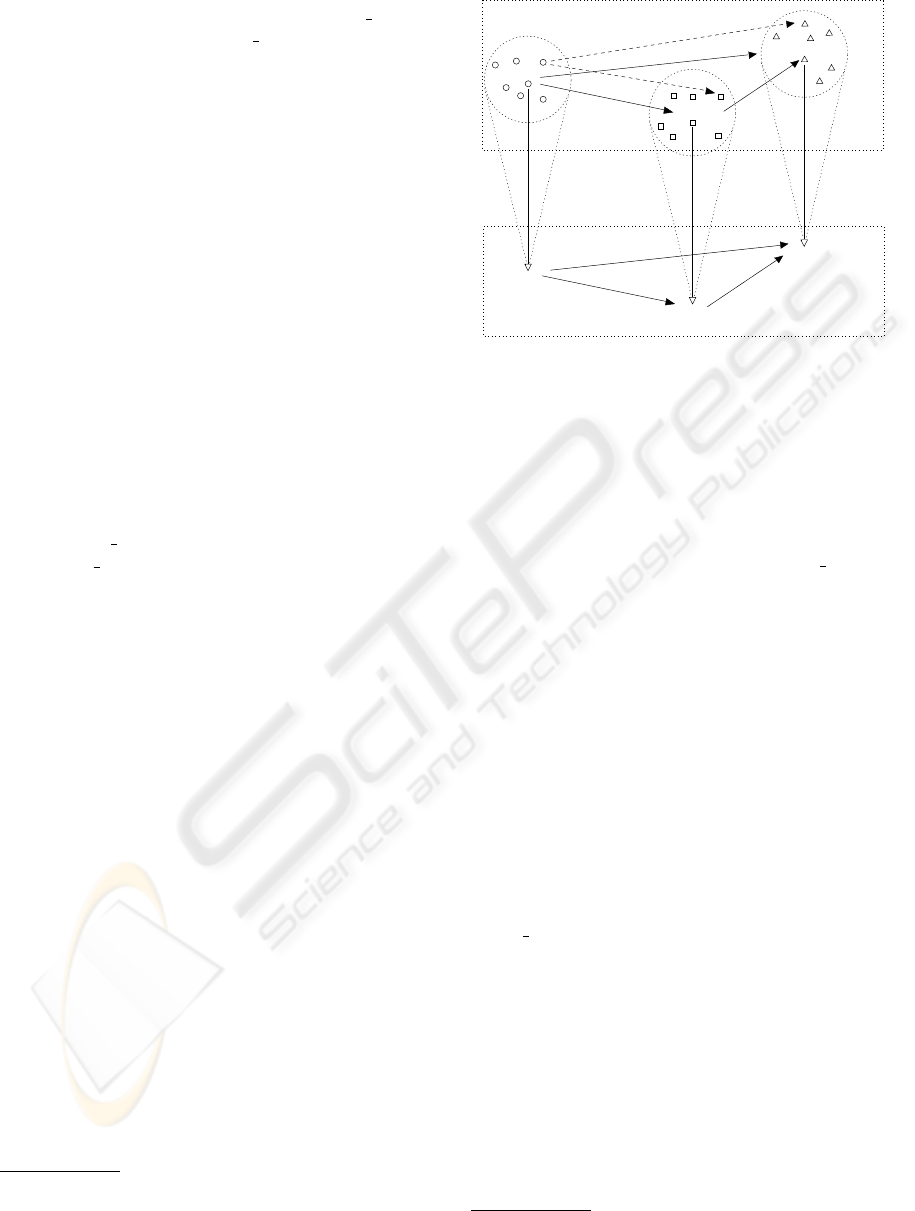
V8 and V6. Similar situation is seen for turbo engine

– squares and turboV8, and car

turbo – triangles and

Porsche911Turbo. There are also morphisms f, g, k

between protoforms, and morphisms , f’, g’, k’, f”,

g” between instances.

Fig. 9 illustrates what it means that instances are

ﬁbers over protoforms, and how this fact inﬂuences

relationships between protoforms and instances. A

few interpretations are included here. The ﬁrst one is

based on the deﬁnition of opﬁbration

, and the others

on its consequences:

• let us assume that the morphism f exists and that

the system receives a piece of information V8

which is identiﬁed as the instance of the engine;

this means that there is a morphism f’ such that

there should be two morphisms g’ and k inducing

a unique morphism k’;

• if a new piece of knowledge V6 appears, and it is

an instance of the protoform engine, then the sys-

tem should search for morphisms between this in-

stance and other instances, this search is induced

by the existence of morphisms between engine (f)

and turbo

engine (g), as well as between engine

and car

turbo; the system will constantly search

for these morphisms (f” and g” in Fig. 9) until all

relations identiﬁed in the deﬁnition of opﬁbration

are satisﬁed;

• if a morphism (connection) is found between two

instances that belong to the models of different

protoforms not related to each other, the system

would treat this morphism as a ”hint” that both

protoforms should connected; as above, the sys-

tem will search for such a morphism until all re-

lations identiﬁed in the deﬁnition of opﬁbration

are satisﬁed, and the correctness of this new mor-

phism is validated.

8 CONCLUSIONS

This paper presents preliminary results of the work

on application of the ADT and category theory to the

concepts of protoforms and instances. It has been

shown that such application is feasible and promises

a number of beneﬁts. The most important beneﬁts

include a systematic approach to dealing with proto-

forms and their instances; a formal way of merging

protoforms and building new ones; and a formal way

Fig. 9 can be used to deﬁne opcartesian morphism re-

quired for deﬁnition of opﬁbration. As it was stated in Sec-

tion 3.2, this deﬁnition is a dual to ﬁbration. For details

please look (Barr and Wells, 1999).

g’

engine

turbo_engine

car_turbo

f’

Instances

Protoforms

k’

turboV8

Porsche911Turbo

Figure 9: An example of knowledge system built based on

the categories Protoforms and Instances (”balloons” rep-

resent ﬁbers over protoform signatures).

of validating correctness of newly established connec-

tions between protoforms and instances.

Additional work is needed towards a full utiliza-

tion of such concepts as speciﬁcation of protoforms,

and application of Specware

(Kestrel

Institute,

2004), for development of protoform-based systems.

REFERENCES

Barr, M. and Wells, C. (1999). Category Theory for Com-

puting Science. Les Publications CRM, Montreal.

Fiadeiro, J. L. (2005). Categories for Software Engineering.

Springer-Verlag, Berlin.

Jacobs, B. (2001). Categorical Logic and Type Theory. El-

sevier, Amsterdam.

Kacprzyk, J. and Zadrozny, S. (2005). Linguistic database

summaries and their protoforms: towards natural lan-

guage based knowledge discovery tools. In Informa-

tion Sciences, volume 173, pages 281–304.

Kestrel

Institute (2004). Specware 4.1 User’s Manual.

Kestrel Development Corp., Palo Alto, California.

Yager, R. R. (2006). Knowledge trees and protoforms in

question answering systems. In Journal of the Ameri-

can Society for Information Sciences.

Zadeh, L. A. (2002). A prototype-centered approach to

adding deduction capabilities to search engines - the

concept of a protoform. In BISC Seminar, University

of California, Berkeley.

An automated software development system based on

principles of ADT and category theory.

ICSOFT 2007 - International Conference on Software and Data Technologies

254