
A PARAMETERIZED GENETIC ALGORITHM IP CORE DESIGN
AND IMPLEMENTATION
K. M. Deliparaschos, G. C. Doyamis and S. G. Tzafestas
School of Electrical and Computer Engineering, National Technical University of Athens
Iroon Polytechneiou 9,15780, Zographou Campus, Athens, Greece
Keywords: Genetic Algorithm (GA), Travelling Salesman Problem (TSP), Field Programmable Gate Array (FPGA)
chip, Very High–speed Integrated Circuits Description Language (VHDL), Intellectual Property (IP) core.
Abstract: Genetic Algorithm (GA) is a directed random search technique working on a population of solutions and
based on natural selection. However, its convergence to the optimum may be very slow for complex
optimization problems, especially when the GA is software implemented, making it difficult to be used in
real time applications. In this paper a parameterized GA Intellectual Property (IP) core is designed and
implemented on hardware, achieving impressive time–speedups when compared to its software version. The
parameterization stands for the number of population individuals and their bit resolution, the bit resolution
of each individual’s fitness, the number of elite genes in each generation, the crossover and mutation
methods, the maximum number of generations, the mutation probability and its bit resolution. The proposed
architecture is implemented in a Field Programmable Gate Array Chip (FPGA) with the use of a Very-High-
Speed Integrated Circuits Hardware Description Language (VHDL) and advanced synthesis and place and
route tools. The GA discussed in this work achieves a frequency rate of 92 MHz and is evaluated using the
Traveling Salesman Problem (TSP) as well as several benchmarking functions.
1 INTRODUCTION
Genetic Algorithms (GAs), initially developed by
Holland (Holland 1975), are based on the notion of
population individuals (genes/chromosomes), to which
genetic operations as mutation, crossover and elitism
are applied. Genetic algorithms obey Darwin’s natural
selection law i.e., the survival of the fittest. GAs have
been successfully applied to several hard optimization
problems, due to their endogenous flexibility and
freedom in finding the optimal solution of the problem
(Mitchell 1996, Goldberg 1989).
However, the most serious drawbacks of software-
implemented GAs are both the vast time and system
resources consumption. Keeping that in mind, a
multitude of hardware-implemented GAs have been
evolved mainly during the last decade, exploiting the
rapid evolution in the field of the Field Programmable
Gate Arrays (FPGAs) technology and achieving
impressive time-speedups.
This paper deploys the design and hardware
implementation of a parameterized GA Intellectual
Property (IP) core (Semiconductor intellectual property
core n.d.) on an FPGA chip. The genetic operators
applied to the genes of the population are crossover,
mutation and elitism, whose employed method is
parametrically selected. The designed selection
algorithm is the “Roulette Wheel Selection Algorithm”.
The FPGA chip used in this work is a Xilinx
XC3S1500–4FG676C Spartan-3 FPGA (Xilinx 2003).
A software implementation of the designed GA using
the Matlab Platform has also been developed to
produce input and output test vectors for the
performance evaluation of the hardware implemented
GA using several benchmark functions, described
below. Finally, after adapting the proposed hardware
implemented GA to the Traveling Salesman Problem
(TSP), a successful solution to it has been found.
2 GA HARDWARE
ARCHITECTURE
This section describes and explains analytically the
various hierarchical modules of the presented GA
architecture.
417
M. Deliparaschos K., C. Doyamis G. and G. Tzafestas S. (2007).
A PARAMETERIZED GENETIC ALGORITHM IP CORE DESIGN AND IMPLEMENTATION.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 417-423
Copyright
c
SciTePress
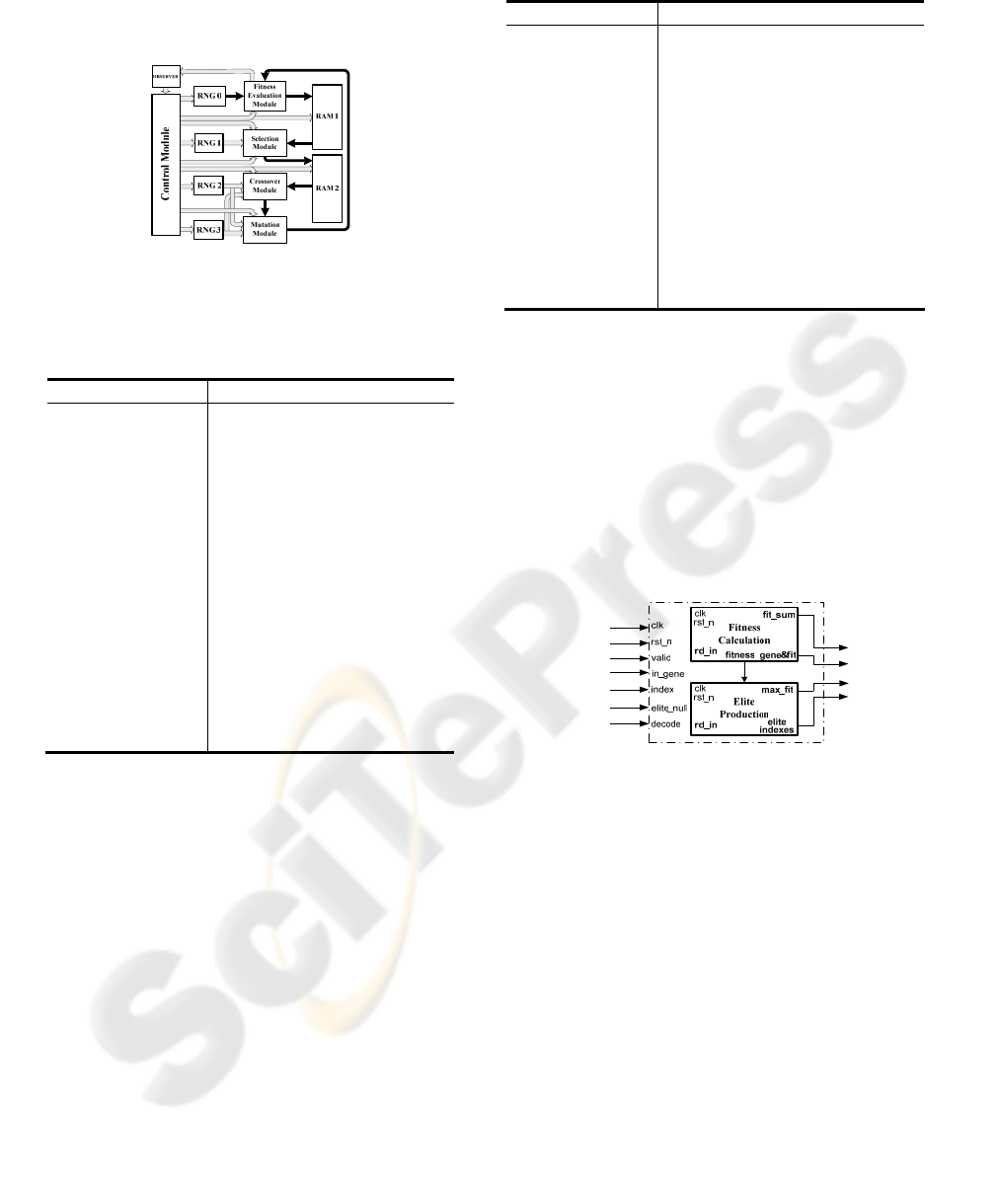
2.1 System Overview
A high level architectural structure of the system is
shown in Figure 1.
Figure 1: High level architectural structure.
2.2 GA Characteristics
Table 1: GA Characteristics.
Parameter name Description
genom_lngt Chromosome length in bits
score_sz Fitness value bit resolution
pop_sz Population size
scaling_factor_res
Bit resolution of the random
number used in RWS
algorithm
elite Number of elite offsprings
mr Mutation rate
mut_res
Bit resolution of the random
number used in mutation
fit_limit Fitness limit
max_gen Maximum generations number
inv_type
Type of the inversion of
the fitness value
(used only in TSP)
1: division 2: subtraction
2.3 GA Architecture
As shown in Figure 1, the architecture is broken into
separate blocks each one of which performs a
particular task, coordinated by the control block.
Moreover, they send back signals to the control
module notifying their state i.e., ready out signals.
2.3.1 Control Module
In order to assure, control and synchronize the order
of execution of the several hardware implemented
modules of the proposed GA architecture, a control
module has been implemented for that reason. This
block produces and feeds all other modules with the
needed control signals using a nine-state Mealy state
machine (Zainalabedin 1998). The task performed
by each of the nine states, is described in Table 2.
Table 2: Diverse states of the implemented state machine.
State Description
clear_ram Clear RAM 1
fill_ram
Fill RAM 1 with a random gene
to create the initial population
fit_eval
Fitness evaluation of the input
gene and generation of the elite
offsprings’ indexes
sel
Selects one parent among the
genes of the current population
cross Apply crossover operation
mut Apply mutation operation
done Check of the termination criteria
read_write_ram_1 Read/write RAM 1
read_write_ram_2 Read/write RAM 2
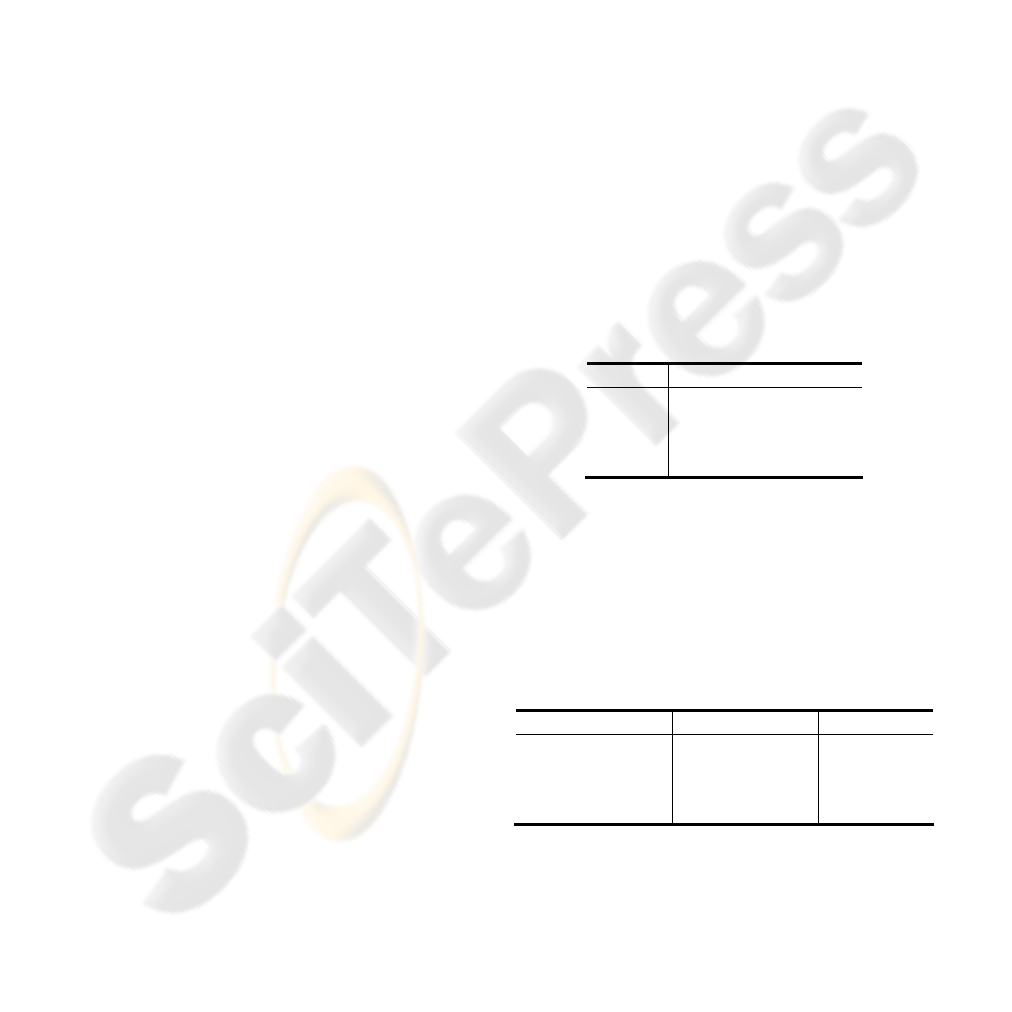
2.3.2 Fitness Evaluation Module
This section describes the fitness evaluation module,
which functions every time a new population of
individuals is formed. This block performs two
separate tasks; on the one hand it calculates the
fitness of each individual according to the given
fitness function and, on the other, it performs elitism
on the current population producing the elite genes
for the next generation. Having that in mind, the
structural architecture of this module consists of two
sub-modules as shown in Figure 2.
Figure 2: High level architectural structure.
The one is used for fitness calculation and the
other for performing elitism. The above mentioned
modules are externally connected to the remaining
GA architecture, so as to allow any further fitness
functions without affecting the rest of the design.
Furthermore, the module outputs both the sum of
fitnesses and the maximum fitness of the current
population as well as the RAM indexes of the elite
genes. The number of elite genes is parametrically
set. In order for an individual to become an elite
gene of the next generation, i.e., to survive in the
next generation, it has to be the fittest among the rest
individuals.
2.3.3 Selection Module
This section describes the selection module, which
operates after the fitness evaluation of the individuals
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
418
of the current population has ended and is controlled by
the control module. The selection block, connected to
both RAMs, implements the Roulette Wheel Selection
Algorithm (RWS) (Koza et al. 1999, Mitchell 1996).
The selection block will keep on selecting parents
till the number of them suffices to produce a new
population with an equal number of individuals like the
one in the current population.
2.3.4 Crossover Module
This section describes the crossover module, which
runs after the selection module has completed its task
and applies the crossover operation to the selected
parents. The crossover method to be implemented is
parametrically employed. There are diverse crossover
strategies reported in literature (Koza et al. 1999,
Tzafestas 1999). The present implementation includes
three different crossover methods, i.e., single point, two
point and uniform crossover.
The crossover module needs a couple of random
numbers (random crossover points, random mask),
according to the method employed, in order to apply
the desired crossover operation. As a result two random
number generators are used for that reason. The former
produces the crossover points and the other the mask
needed for the application of uniform crossover to the
parents. The crossover block outputs one offspring in
each execution, produced by two of the selected
parents.
2.3.5 Mutation Module
This section describes the mutation module, which
functions after the crossover module has completed its
task and applies the parametrically employed mutation
method to the crossovered offsprings, i.e., the
offsprings produced by crossover module. Various
mutation strategies are reported in literature (Koza
1999, Tzafestas 1999). The proposed design includes
three different mutation methods, i.e., single point,
masked and uniform mutation.
The mutation module requires a couple of random
numbers (random mutation points, random mask,
random numbers p
r,i
), according to the method
employed so as to apply the desired mutation operation.
For this reason two random number generators are
needed. The former produces the mutation points and
the other a random binary mask. The latter RNG also
generates the necessary random number p
r
, in order to
decide if mutation operation will be applied, i.e., only if
its value is less or equal to the parametrically set
mutation probability p
m
, will mutation be applied to the
offsprings. If the mutation method employed is uniform
mutation, it also generates the essential random
numbers for uniform mutation. The mutation block
outputs one offspring in each execution produced by
processing one offspring, result of crossover, each time.
2.3.6 Observer Module
This section describes the observer module, which
executes each time a new population has been
formed. This block determines the continuation of the
algorithm, checking if the parametrically set stopping
criteria, i.e., maximum generations, fitness value
limit, have been met.
2.3.7 Random Number Generators
This section describes the random number generator
modules, which feed most of the described modules
above with random numbers. This block implements
a Linear Feedback Shift Register (LFSR) generator,
whose sequence length is parametrically set. Four
random number generators (RNG) are used to
produce both the initial random generation and the
necessary random numbers. The maximum length of
the random generated sequence is 128 bits, while the
specific characteristics of the four RNGs used in our
design are shown in Table 3.
Table 3: Characteristics of the used RNGs.
RNG LFSR length
RNG 0 genom_lngt
RNG 1 scaling_factor_res
RNG 2 genom_lngt + mut_res
RNG 3 2•log2(genom_lngt)
2.3.8 Random Access Memory (RAM)
This section describes the Random Access Memory
(RAM) modules, RAM 1 and RAM 2, which store
the current population and the selected parents
respectively. Both the address and data widths are
parametrically set, as shown in Table 4.
Table 4: Parameters of RAM 1 and RAM 2.
RAM Address width Data width
RAM 1
(population RAM)
genom_lngt
genom_lngt
+ score_sz
RAM 2
(parents RAM)
2•(pop_sz-elite) genom_lngt
3 DESIGN FLOW FOR THE GA
This section presents the design flow, illustrated in
Figure 3, in a top-down manner (Deliparaschos et al.
2006), followed in our design. In a top-down design,
one first concentrates on specifying and then on
A PARAMETERIZED GENETIC ALGORITHM IP CORE DESIGN AND IMPLEMENTATION
419
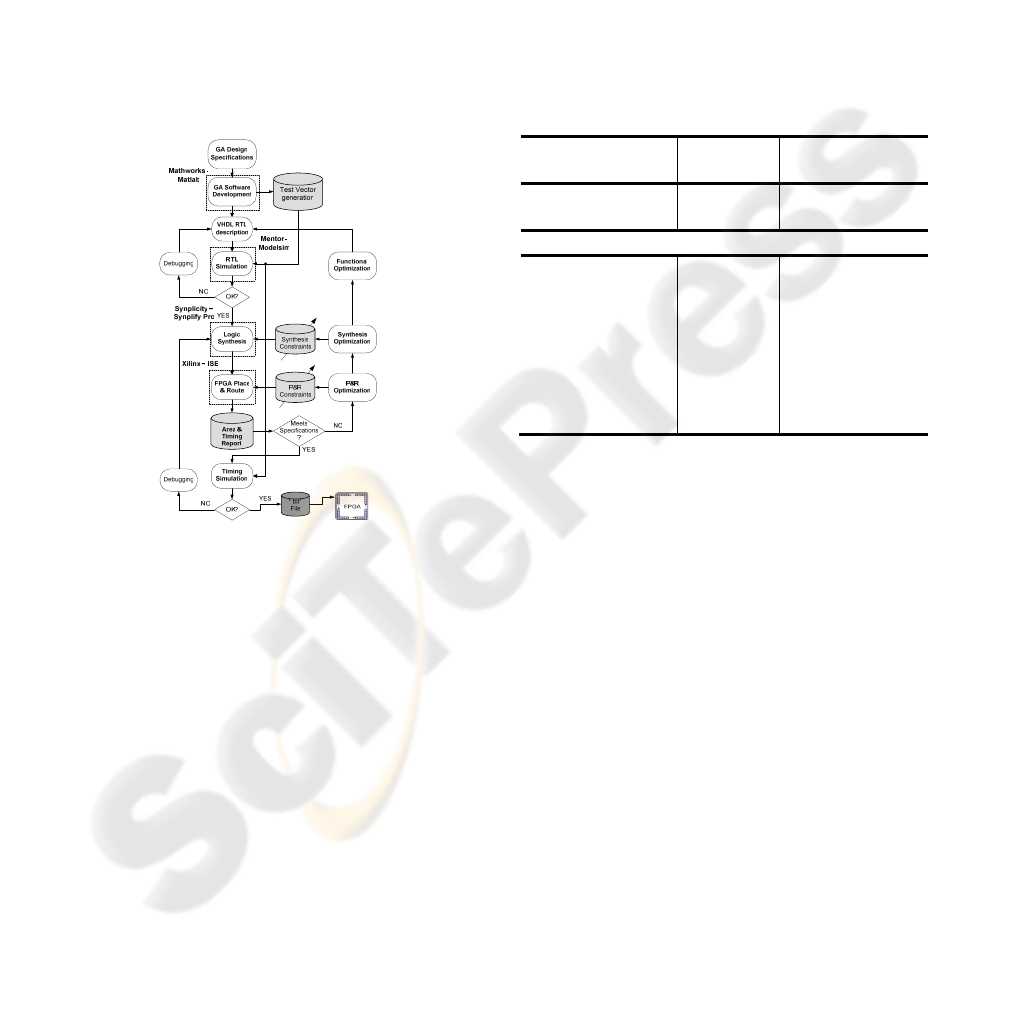
designing the circuit functionality (Sjoholm et al.
1997). The starting point of the design process is the
system level modelling of the proposed GA, so as to
evaluate the proposed model and to extract valuable
test vector values to be used later for RTL and timing
simulation. Special attention has been paid on the
coding of the different blocks, since we aim at writing
a fully parameterized GA code. An RTL simulation
has been performed to ensure the correct functionality
of the circuit. Next, logic synthesis has been done,
where the tool first creates a generic (technology-
independent) schematic on the basis of the VHDL
code and then optimizes the circuit to the FPGA
specific library chosen (Spartan-3 1500-4FG676). At
this point, area and timing constraints and specific
design requirements must be defined as they play an
important role for the synthesis result.
Figure 3: Design Flow.
Following, the Xilinx ISE place and route (PAR)
tool accepts the input netlist file (.edf), generated with
Synplify Pro synthesis tool, translates and maps our
design on the FPGA device. Finally, it places and
routes the FPGA producing output for the bitstream
generator (BitGen). The latter program generates a
bitstream (.bit) for Xilinx device configuration.
Before programming the FPGA file, a timing
simulation is performed to ensure that the circuit
meets the timing requirements set and works
correctly.
4 IMPLEMENTATION RESULTS
This section describes the implementations results of
the designed GA. After the synthesis of the design,
ISE translates, maps, and places and routes our design
to the FPGA device. The FPGA utilization for both
the GA and the GA adapted to the TSP produced by
ISE are shown in Table 5.
The hardware implementation of the proposed GA
achieves an internal clock frequency rate of 92 MHz
(10,8 ns) while the adapted GA to the TSP achieves
an internal clock frequency rate of 91 MHz (11 ns).
Moreover, 2.450 ns (2,4 μs) and 14.391 ns (14,3 μs)
are required to form a new generation of 8 individuals
in the former and latter version of the GA
respectively. Finally, the VHDL codes for the GA
models presented here are fully parameterized,
allowing us to generate and test the GA models with
different specification scenarios.
Table 5: FPGA Utilization for the implemented GAs.
Logic Utilization GA
GA
(adapted to TSP)
Slice flip flops 681 (2%) 1045 (3%)
4 – Input LUTs 1086 (4%) 1630 (6%)
Logic Distribution
Occupied slices 892 (6%) 1305 (9%)
4 – Input LUTs 1116 (6%) 1686 (6%)
Used as logic 1086 1630
Used as route-thru 6 4
Used as 16x1 ram 24 52
Bonded IOBs 59 (12%) 53 (10%)
MULT 18x18s 1 (3%) 3 (9%)
GCLKs 1 (12%) 1 (12%)
5 EVALUATION RESULTS
The evaluation of the system performance has been
made both by solving the TSP problem and by
optimizing several benchmark functions (Digalakis
et al. 2000, Zhang and Zhang 2000), which are
noted in section 5.2.2. In order to evaluate the
performance of the implemented GA using the TSP,
we firstly have to adapt the hardware to the TSP
(section 5.1) and secondly to write a software
version of the hardware implemented GA, which
will also be adapted to the TS problem. Both the
software version of the GA and the one adapted to
the TSP have been developed on Matlab Platform.
5.1 GA Hardware Adaptation to the TSP
According to the definition of the TSP (Pham and
Karaboga 2000), each city should be visited only
once. So every gene of the population, which contains
the towns to be visited in sequence, must contain each
town only once. Since our genes are unique, we
cannot possibly use the above mentioned crossover
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
420
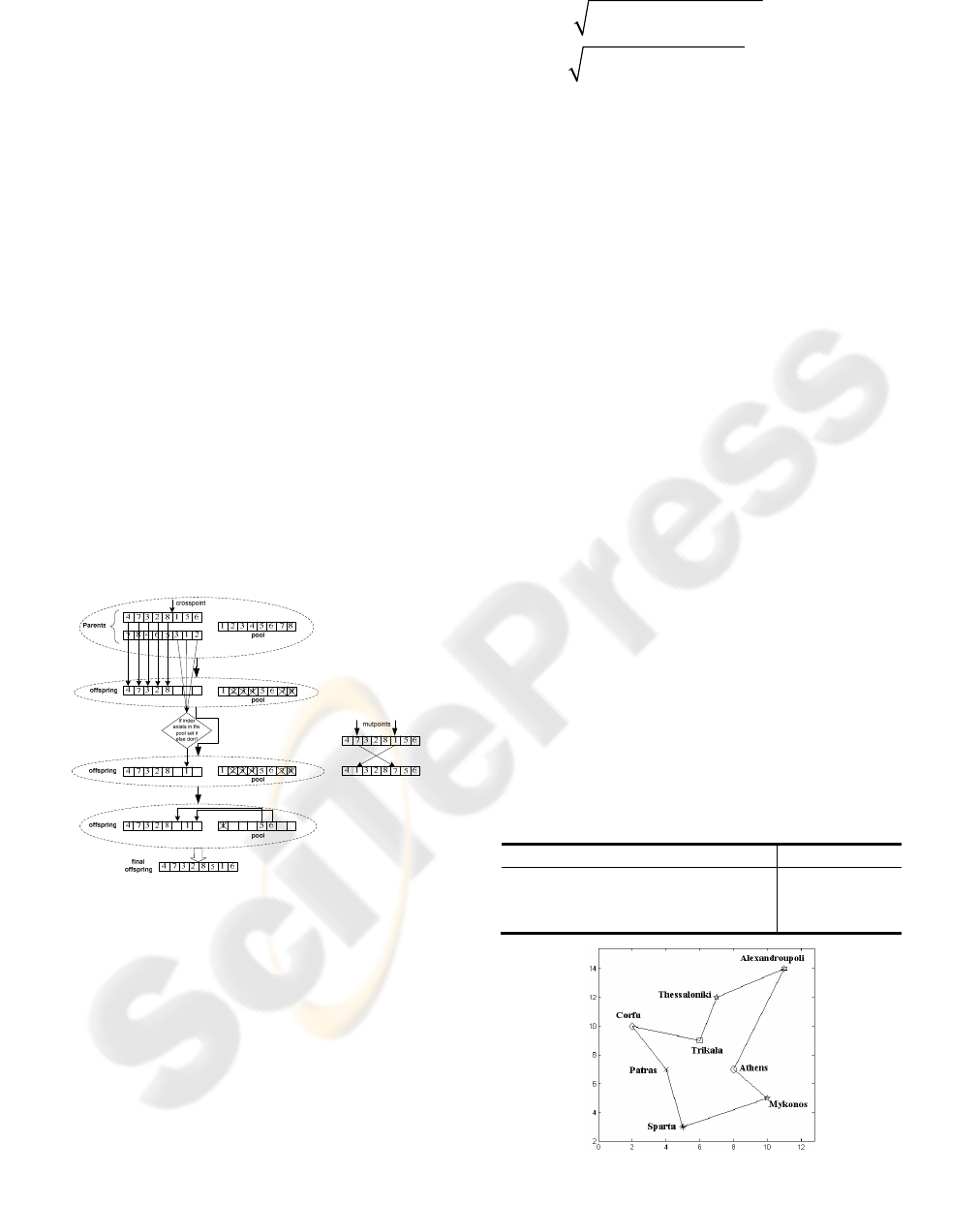
and mutation techniques, but new crossover and
mutation methods must be developed (explained
below) (Martel 2006).
The crossover operator uses a pool of indices of
the towns. In order to keep the uniqueness of the
visited cities used indices will be removed from the
pool. The offspring produced after the application of
crossover to the parents, is formed via the following
procedure: In the beginning a random crossover
point is generated and then the town indices of the
first parent are added to the offspring starting from
the crossing site, to the head of the gene. The afore-
mentioned indices are removed from the pool.
Afterwards the right side of the gene is filled by
checking whether the town indices in the right side
of the second parent are contained in the pool. If a
town index is still free, i.e. exists both in the pool
and the second parent, we place it in the offspring
and remove it from the pool; otherwise we skip it
and leave its place in the offspring empty till we
reach the tail of the gene. Finally empty places of the
offspring are randomly filled with the town indices
remaining in the pool. The developed mutation
operator utilizes two random generated mutation
points and simply swaps the town indices stored at
these points of the gene. The described methods for
8 cities are depicted in Figure 4.
Figure 4: Crossover and mutation operations for TSP.
The fitness evaluation function implemented here, is
the computation of the sum over the number of
towns (N) of the square of the Euclidean distances
between two adjacent towns according to the
computed tour, as shown in equation (1). We
compute the square of the Euclidean distance in
order to avoid the hardware implementation of the
square root, since it is not necessary as we do
nothing but merely compare the fitnesses among the
chromosomes.
()()
(
)
()()
()
11
2
1
22
11
1
2
22
][1,
_
NN
N
jiiii
i
fit x x y y
x
x y y j pop sz
−
++
=
=−+−
−+− ∈
+
∑
(1)
Since we seek the optimal minimum path
connecting the given towns and the GA is designed to
result in the gene with the maximum fitness instead,
i.e., with the maximum sum of Euclidean distances,
we have either to invert the computed fitness or to
subtract the fitness from its highest value, according
to the resolution of bits adopted for the binary coding
of it, i.e. 2
score_sz
-1 (See Table 1), in order to get higher
values for smaller path lengths. The method for the
inversion of the fitness to be implemented is selected
through a generic in the VHDL code (inv_type).
5.2 Results
The performance evaluation of the proposed GA using
the TSP and various benchmark functions follow.
5.2.1 TSP
The performance evaluation of the proposed GA
using the TSP has been performed by comparing the
time needed for the software version developed and
the one needed for the hardware implementation to
find the optimal solution. The results for eight cities,
60 generations and 32 individuals are summarized in
Table 6, where an impressive speedup ratio of 11.035
can be observed. Figure 5 depicts the map of the 8
cities used, which are existing cities of the greek
territory. The algorithm was also tested using the
benchmark burma14 derived from the TSPLIB
(Gerhard n.d.), and the result is depicted in Figure 6.
Table 6: Software vs. Hardware GA.
GA version Time (msec)
Hardware (11 nsec) 1,702
Software
(Pentium 4 3,2 GHz 1Gb RAM )
18.783
Figure 5: Map of the cities used in the TSP.
A PARAMETERIZED GENETIC ALGORITHM IP CORE DESIGN AND IMPLEMENTATION
421
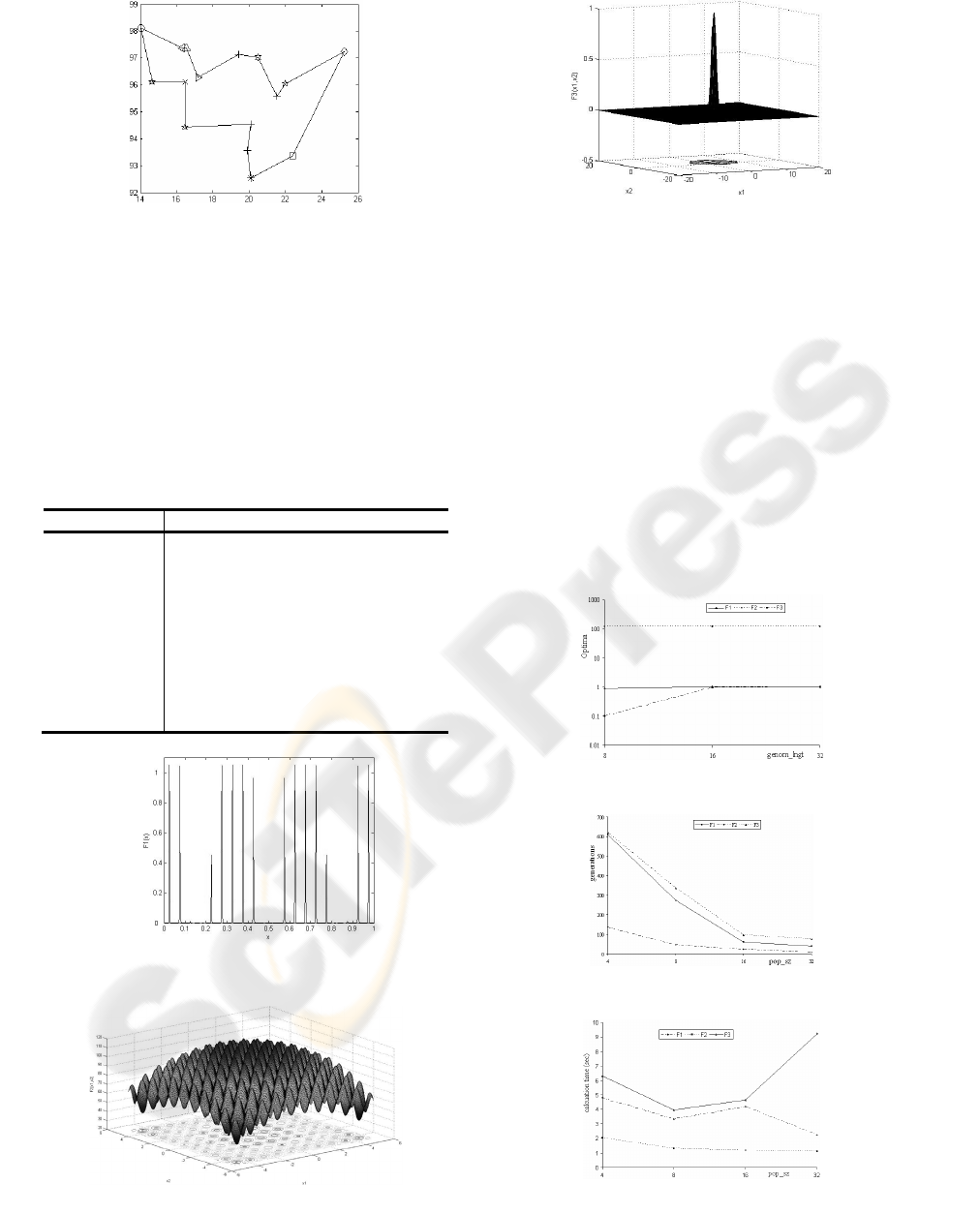
Figure 6: TSP solution of burma14 benchmark.
5.2.2 Benchmark Functions
Several benchmark functions are known in the
literature (Digalakis and Margaritis 2000, Zhang et
al. 2000) for evaluating the performance of a GA,
i.e. its ability to reach the optimum of an objective
function. In our case we have tested the proposed
GA using the following functions, which are noted
in Table 7 and depicted in figures 7–9.
Table 7: Benchmarking functions.
Name Function type
F1:
Zhang Zhang
() ( )
()
()
sin sin
,
xx
x
ππ
−+
∈
20
20 20
12 3 20
01
F2:
Rastrigin
()
()
cos
,,
ii
i
i
x
x
x
π
=
−−
−≤≤
∑
2
2
1
100 10 2
512 512
F3:
Easom
()
()
()
cos
,
i
i
x
i
i
i
A
xA
xe
A
π
=
−−
=
⎛⎞
∑
−≤ ≤
⎛⎞
⎜⎟
×
⎜⎟
⎜⎟
∈
⎝⎠
⎝⎠
∏
2
2
1
2
1
10 100
Figure 7: Zhang Zhang function (F1).
Figure 8: Rastrigin function (F2).
Figure 9: Easom function (F3).
In the following figures the results of a number of
experiments using the above mentioned functions are
presented. Figure 10 shows the effect of the
chromosome length (genom_lngt) on the optimal
solution found, while Figure 11 depicts the effect of the
population size (pop_sz) on the generations needed by
the algorithm to converge. Finally the influence of the
population size on the calculation time is shown in
Figure 12. We also have to note that the precision of the
optimum value found by the proposed GA depends on
the chromosome length adopted in each experiment. A
length of 16 and 32 bits for evaluating one and two-
variable benchmark functions, respectively, is observed
to give high accuracy on the result in relatively low
calculation times.
Figure 10: Estimated optima vs. chromosome length.
Figure 11: Estimated generations vs. population size.
Figure 12: Estimated calculation time vs. population size.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
422

6 CONCLUSION
In this work we presented a fully parameterized
Genetic Algorithm IP in terms of the number of
population individuals (pop_sz) and their resolution in
bits (genom_lngt), resolution in bits of the fitness
(score_sz), number of elite genes in each generation
(elite), method used for crossover (cross_method) and
mutation (mut_method), number of maximum
generations (max_gen), mutation probability (mr) and
its resolution in bits (mut_res), as well as the resolution
in bits of the scaling factor used by the RWS algorithm.
This parameterization allows the adaptation of the GA
to any problem specifications without any further
change to the developed VHDL code. Furthermore, the
proposed hardware implemented GA operates at a
clock rate of 92 MHz (10,8 ns) and achieves a
noteworthy speedup when compared to its software
version. Additionally, the hardware area required for
the implementation and the requirements of RAM are
kept small according to the PAR report (see Table 5).
Compared to other GAs hardware implementations
(Zhu et al. 2006, Aporntewan and Chongstitvatana
2001, Lei et al. 2002, Tang and Yip 2002), our design
operates at a clock frequency up to five times faster and
implements more than one crossover and mutation
methods, which can be changed during its execution.
Moreover, our design utilizes more parameters and is
evaluated not only by using benchmarking functions
but also by solving the NP-complete Travelling
Salesman Problem.
REFERENCES
Aporntewan, C., Chongstitvatana, P., 2001. A hardware
implementation of the Compact Genetic Algorithm.
Proceedings of the 2001 Congress on Evolutionary
Computation, 1, pp. 624–629.
Deliparaschos, K.M., Nenedakis, F.I., Tzafestas, S.G.,
2006. Design and implementation of a fast digital
fuzzy logic controller using FPGA technology.
Journal of Intelligent and Robotics Systems, 45, pp.
77–96.
Digalakis, J.G., Margaritis, K.G., 2000. An experimental
study of benchmarking functions for genetic
algorithms. in: 2000 IEEE Int. Conference on Systems,
Man, and Cybernetics, 5, pp. 3810–3815.
Gerhard, R., TSP libraries. Department of Computer
Sciences, University of Heidelberg. Available from:
http://www.iwr.uniheidelberg.de/groups/comopt/softw
are/TSPLIB95/
Goldberg, D.E., 1989. Genetic Algorithms in Search
Optimization and Machine Learning. Reading, MA:
Addison-Wesley.
Holland, J.H., 1975. Adaptation in Natural and Artificial
systems: An Introductory Analysis with Application to
Biology, Control, and Artificial Intelligence. Ann
Arbor, MI: University of Michigan Press.
Koza, J.R., 1992. Genetic Programming: On the
programming of computers by means of natural
selection. Cambridge, MA: MIT Press.
Koza, J.R., Bennett III, F.H., Andre, D., Keane, M.A.,
1999. Genetic Programming III: Darwinian Invention
and Problem Solving. San Francisco, CA: Morgan
Kaufmann Publishers.
Lei, T., Zhu M.-C., Wang J.-X., 2002. The hardware
implementation of a genetic algorithm model with
FPGA. in: 2002 IEEE International Conference on
Field–Programmable Technology (FPT), pp. 374–377.
Mitchell, M., 1996. An Introduction to Genetic
Algorithms. Cambridge, MA: MIT Press.
Martel, E., Solving Travelling Salesman Problems using
Genetic Algorithms. Available from: http://ai-
depot.com/Articles/51/TSP.html
Pham, D.T., Karaboga, D., 2000. Intelligent Optimization
Techniques: Genetic Algorithms, Tabu Search,
Simulated Annealing and Neural Networks. London,
UK: Springer.
Sjoholm, S., Lindh, L., 1997. VHDL for Designers.
London, UK: Prentice Hall.
Tang, W., Yip, L., 2004. Hardware implementation of
genetic algorithms using FPGA. in: MWSCAS '04, The
2004 47th Midwest Symposium on Circuits and
Systems, 1, pp. 549–552.
Tzafestas, S.G., 1999. Soft Computing in Systems and
Control Technology. 18, London, UK: World
Scientific.
Wikipedia, Semiconductor intellectual property core.
Available from:
http://en.wikipedia.org/wiki/Semiconductor_intellectu
al_property_core
Xilinx, 2003. Spartan-3 FPGA Family: Complete Data
Sheet - DS099.
Available from:
http://www.xilinx.com/bvdocs/publications/ds099.pdf
Zainalabedin, N., 1998. VHDL: Analysis and Modeling of
Digital Systems. NY: Mc Graw-Hill International.
Zhu, Z., Mulvaney, D., Chouliaras, V., 2006. A novel
genetic algorithm designed for hardware
implementation. Int. Journal of Computational
Intelligence, 3, number 4.
Zhang, L., Zhang, B., 2000. Research on the mechanism
of genetic algorithms. Journal of Software, 11(7),
pp.945–952.
A PARAMETERIZED GENETIC ALGORITHM IP CORE DESIGN AND IMPLEMENTATION
423
