SELECTIVE IMAGE DIFFUSION FOR ORIENTED PATTERN
EXTRACTION
A. Histace
ETIS UMR CNRS 8051, ENSEA-UCP, 6 avenue du Ponceau, 95014 Cergy, France
V. Courboulay, M. M
´
enard
L3i, University of La Rochelle, Pole Sciences et Technologie, 17000 La Rochelle, France
Keywords:
Image Diffusion, Extreme Physical Information, Oriented Pattern Extraction, Selectivity.
Abstract:
Anisotropic regularization PDE’s (Partial Differential Equation) raised a strong interest in the field of image
processing. The benefit of PDE-based regularization methods lies in the ability to smooth data in a nonlinear
way, allowing the preservation of important image features (contours, corners or other discontinuities). In
this article, a selective diffusion approach based on the framework of Extreme Physical Information theory is
presented. It is shown that this particular framework leads to a particular regularization PDE which makes it
possible integration of prior knowledge within diffusion scheme. As a proof a feasibility, results of oriented
pattern extractions are presented on ad hoc images. This approach may find applicability in vision in robotics.
1 INTRODUCTION
Since the pioneering work of Perona-Malik (Perona
and Malik, 1990), anisotropic regularization PDE’s
raised a strong interest in the field of image process-
ing. The benefit of PDE-based regularization meth-
ods lies in the ability to smooth data in a nonlin-
ear way, allowing the preservation of important im-
age features (contours, corners or other discontinu-
ities). Thus, many regularization schemes have been
presented so far in the literature, particularly for the
problem of scalar image restoration (Perona and Ma-
lik, 1990; Alvarez et al., 1992; Catt
´
e et al., 1992; Ge-
man and Reynolds, 1992; Nitzberg and Shiota, 1992;
Whitaker and Pizer, 1993; Weickert, 1995; Deriche
and Faugeras, 1996; Weickert, 1998; Terebes et al.,
2002; Tschumperle and Deriche, 2002; Tschumperle
and Deriche, 2005). In (Deriche and Faugeras, 1996)
Deriche and al. propose a unique PDE to express the
whole principle.
If we denote ψ(r,0) : R
2
× R
+
→ R the intensity
function of an image, to regularize the considered im-
age is equivalent to a minimization problem of a par-
ticular PDE which can be seen as the superposition of
two monodimensionnal heat equations, respectively
oriented in the orthogonal direction of the gradient
and in the tangential direction (Eq. (1 and Fig. 1) :
∂ψ
∂t
=
φ
′
(k∇ψk)
k∇ψk
ψ
ξξ
+ φ
′′
(k∇ψk)ψ
ηη
, (1)
where η = ∇ψ/k∇ψk and ξ⊥η and φ : R → R is a
decreasing function.
This PDE is characterized by an anisotropic diffu-
sive effect in the privileged directions ξ and η allow-
ing a denoising of scalar image.
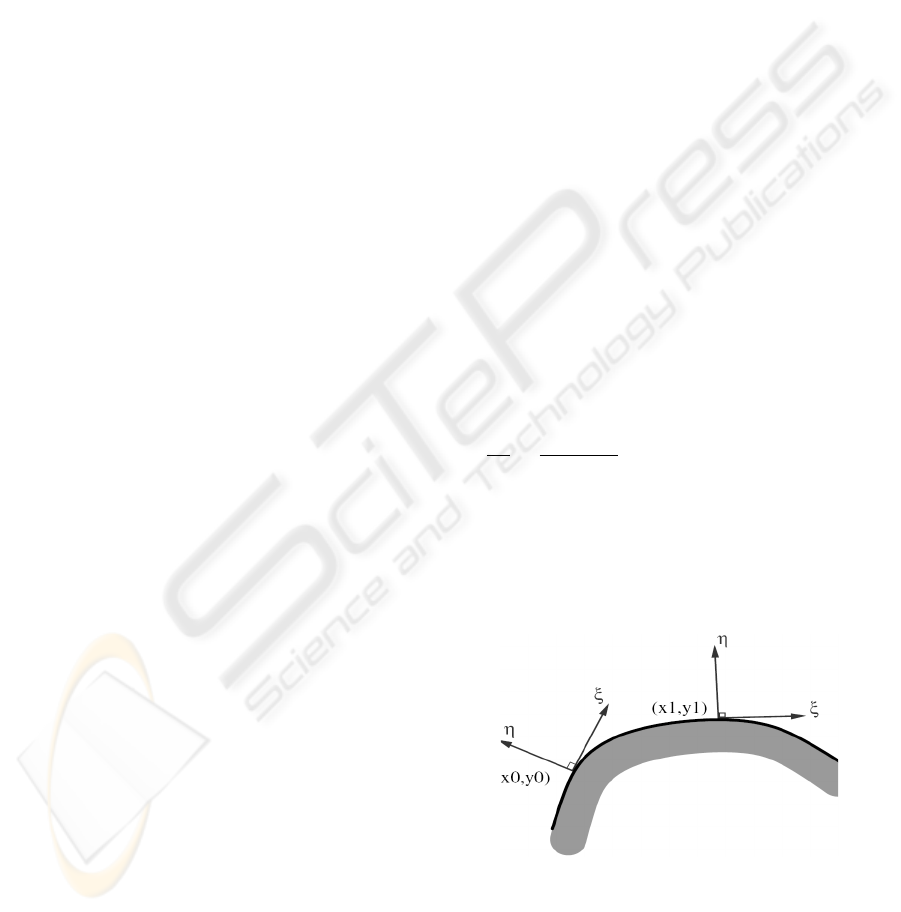
Figure 1: An image contour and its moving vector basis
(ξ,η). Taken from (Tschumperle and Deriche, 2002).
The major limitations of this diffusion process is
its high dependance to the intrinsic quality of the orig-
inal image and the impossibility to integrate prior in-
formation on the pattern to be restored if it can be
270
Histace A., Courboulay V. and Ménard M. (2007).
SELECTIVE IMAGE DIFFUSION FOR ORIENTED PATTERN EXTRACTION.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 270-274
DOI: 10.5220/0001617802700274
Copyright
c
 SciTePress

characterized by particular data (orientation for ex-
ample). Moreover, no characterization of the uncer-
tainty/inaccuracy compromise can be made on the
studied pixel, since the scale parameter is not directly
integrated in the minimisation problem in which relies
the common diffusion equations (Nordstrom, 1990).
In this article we propose an original PDE directly
integrating the scale parameter and allowing the tak-
ing into account of a priori knowledge on pattern to
restore. We propose more particularly, to derive this
PDE, to use a recent theory known as Extreme Phys-
ical Information (EPI) recently developed by Frieden
(Frieden, 1998) and applied to image processing by
Courboulay and al. (Courboulay et al., 2002).
The second section of this article is dealing with
the presentation of EPI and with the obtaining of the
particular PDE. The third one presents a direct appli-
cation to the presented diffusion process which may
find applicability in robotics and automation. Last
part is dedicated to discussion.
2 EPI AND IMAGE DIFFUSION
2.1 EPI
Developed by Frieden, the principle of Extreme Phys-
ical Information (EPI) is aimed at defining a new the-
ory of measurement. The key element of this new
theory is that it takes into account the effect of an
observer on a measurement scenario. As stated by
Frieden (Frieden, 1996; Frieden, 1998), ”EPI is an
observer-based theory of physics”. By observing, the
observer is both a collector of data and an interfer-
ence that affects the physical phenomenon which pro-
duces the data. Although the EPI principle brings new
concepts, it still has to rest on the definition of infor-
mation. Fisher information was chosen for its abil-
ity to effectively represent the quality of a measure-
ment. Fisher information measure was introduced by
Fisher in 1922 (Fisher, 1922) in the context of statisti-
cal estimation. In the last ten years, a growing interest
for this information measure has arisen in theoretical
physics. In his recent book (Frieden, 1998), Frieden
has characterized Fisher information measure as a
versatile tool to describe the evolution laws of physi-
cal systems; one of his major results is that the classi-
cal evolution equations as the Shrodinger wave equa-
tion, the Klein-Gordon equation, the Helmotz wave
equation, or the diffusion equation, can be derived
from the minimization of Fisher information measure
under proper constraint.
Practically speaking, EPI principle can be seen as
an optimization of the information transfer from the
system under measurement to the observer, each one
being characterized by a Fisher Information measure
denoted respectively I and J. The first one is repre-
sentative of the quality of the estimation of the data,
and the second one allows to take into account the ef-
fect of the subjectivity of the observer on the measure.
The existence of this transfer leads to create fluctua-
tions on the acquired data compared to the real ones.
In fact, this information channel leads to the loss of
accuracy on the measure whereas the certainty is in-
creased.
Measure
System
Data
Real data
Acquired data
Information J
Information I
(Fisher Information)
Figure 2: Fisher Information.
The goal of EPI is then to extremize the difference
I − J (i.e. the uncertainty/inaccurracy compromise)
denoted K, called Physical Information of the system,
in order to optimized the information flow.
2.2 Application to Image Diffusion
Application to image diffusion can be illustrated by
Fig. (3).
x
y
x
y
x
y
x
y
Initial Image Scale t
Scale t+dt Convergence Image
∞
ψ
Grey level of a given pixel r
+
ψ
ψ
ψ
ε
ε
Figure 3: Uncertainty/inaccuracy compromise and isotropic
image diffusion. When parameter t → ∞, luminance of all
pixels of the corresponding image is the same and equal to
the spatial average of the initial image.
As far as isotropic image diffusion is concerned,
the uncertainty deals with the fluctuations of the grey
level of a given pixel compared with its real value,
whereas the inaccuracy deals with the fluctuations of
the spatial localisation of a given pixel compared with
SELECTIVE IMAGE DIFFUSION FOR ORIENTED PATTERN EXTRACTION
271

the real one. The two different errors (ε
r
(t) and ε
v
(t))
of Fig. (3) which are introduced all along the diffu-
sion process are characterized by a measure of Fisher
information. Intrinsic Fisher information J will be an
integration of the diffusion constrained we impose on
the processing.
Then, we can apply EPI to image diffusion pro-
cess by considering an image as a measure of char-
acteristics (as luminance, brightness, contrast) of a
particular scene, and diffusion as the observer of this
measure at a given scale. Extreme Physical Informa-
tion K is then defined as follows (Frieden, 1998):
K(ψ) =
dΩdt ×

(∇− A) (∇− A)ψ
2
+ (
∂ψ
∂t
)
2
− ψ
2

,
(2)
where ψ(r, 0) : R
2
× R
+
→ R is the luminance func-
tion of the original image and A a potential vector
representing the parameterizable constrain integrated
within diffusion process.
Extremizing K by Lagrangian approach leads to a
particular diffusion equation given by :
∂ψ
∂t
=
1
2
(∇− A).(∇− A)ψ . (3)
As a consequence, thanks to the possible param-
eterization of A, it is possible to take into account
particular characterized pattern to preserve from the
diffusion process.
2.3 About A
The A potential allows to control the diffusion pro-
cess and introduce some prior constrains during im-
age evolution. For instance, if no constrain are to be
taken into account, we set A as vector null and (Eq.
3) becomes :
∂ψ
∂t
= ∇.∇ψ = △ψ . (4)
which is the well known heat equation characterized
by an isotropic smoothing of the data processed.
In order to enlarge the possibility given by Eq. (3),
the choice we make for A is based on the fact that Eq.
(3) allows a weighting of the diffusion process with
the difference of orientation between the local calcu-
lated gradient and A. More precisely, to explain the
way A is practically implemented, let consider Fig. 4.
The expression of the local gradient ∇ψ in terms
of θ” is, considering Fig. 4 :
∇ψ =
k∇ψkcosθ
′′
k∇ψksinθ
′′
!
, (5)
ψ
A
ψ
θ’
θ’’
θ
⊥
2
3
π
Figure 4: Local geometrical implementation of A in terms
of the local gradient ∇ψ.
and an expression of A in terms of θ’ is :
A =
k∇ψkcosθ
′
k∇ψksinθ
′
!
. (6)
Norm of A is imposed in order to make it possible the
comparison with the gradient. To this point, the most
interesting expression of A would be the one in terms
of θ, which represents the difference angle between A
and the local gradient. If we made so, using trigono-
metrical properties and noticing that θ = |θ
′′
−θ
′
|, we
obtain a new expression for A :
A =
k∇ψk(cosθ
′′
cosθ+ sinθ
′′
sinθ)
k∇ψk(sinθ
′′
cosθ− cosθ
′′
sinθ)
!
. (7)
Eq. (7) could be simplified by integrating the vectorial
expression of the local gradient (Eq. (5)) :
A = ∇ψ.cosθ+ ∇
⊥
3π
2
ψ.sinθ . (8)
From Eq. (8), we could then derive a general expres-
sion for A considering it as a vectorial operator :
A = ∇.cosθ+ ∇
⊥
3π
2
.sinθ , (9)
with θ the relative angle between A et ∇ψ for a
given pixel and ∇
⊥
the local vector orthogonal to ∇
(Fig. 4). This expression only represents the way it
is possible to reexpress A by an orthogonal projection
in the local base. Considering it, Eq. (3) becomes :
∂ψ
∂t
=
∂
2
ψ
∂η
2
.(1− cosθ) +
∂
2
ψ
∂ξ
2
.(1− cosθ) . (10)
One can notice on Eq. (10) that when angle θ = 0
(i.e. A and ∇ψ are colinear), the studied pixel will
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
272

not be diffused for
∂ψ
∂t
= 0. On the contrary, a non-
zero value of θ will lead to a weighted diffusion of
the considered neighborhood of the pixel (Eq. (10)).
As a consequence, by imposing local θ values, it
is possible to preserve particular patterns from the dif-
fusive effect within the processed image.
3 APPLICATION TO ORIENTED
PATTERN EXTRACTION
In this section, we present results obtained on simple
images in order to show the restoration and denoising
potential of the method.
For practical numerical implementation, the pro-
cess of Eq. (10) is discretized with a time step τ. The
images ψ(t
n
) are calculated, with Eq. (10), at discrete
instant t
n
= nτ with n the number of iterations in the
process.
Let first consider an image showing vertical, hor-
izontal, and 45
◦
-oriented dark stripes on a uniform
background (Fig. 5).
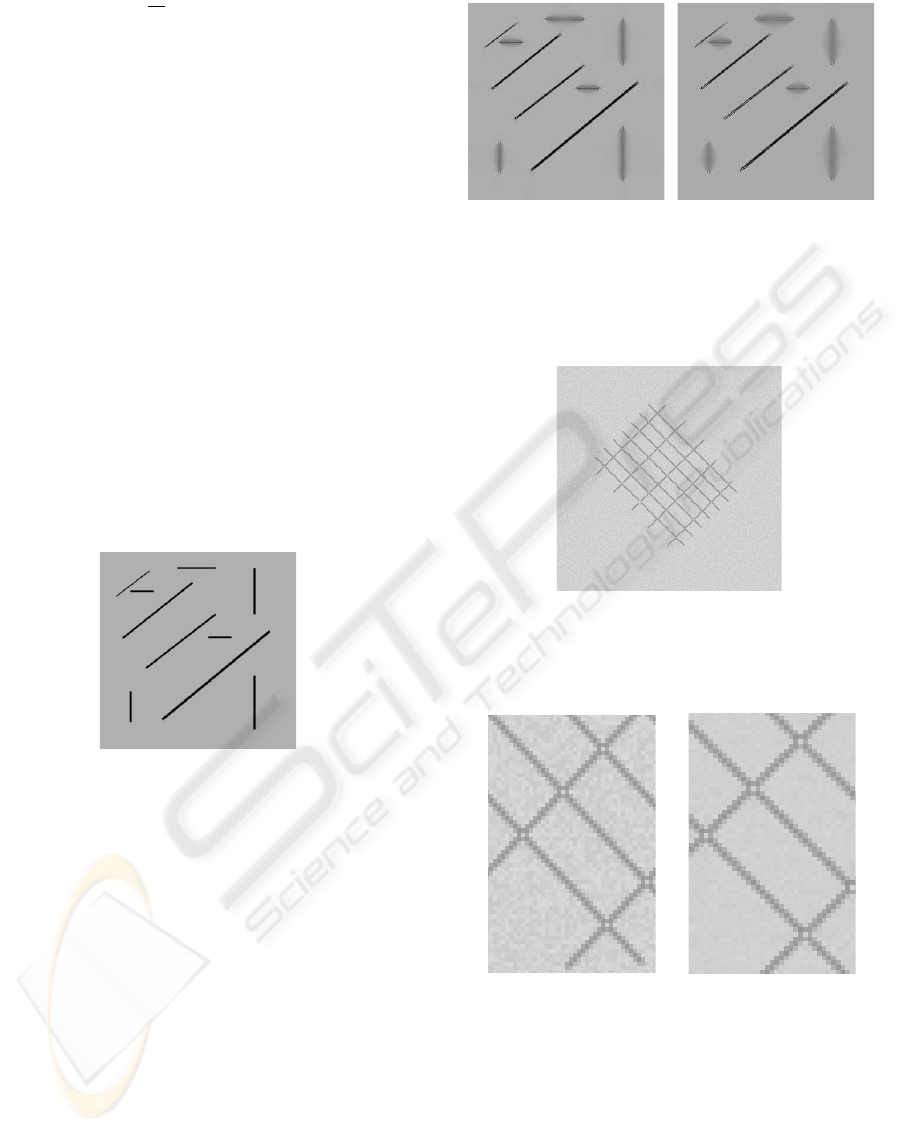
Figure 5: Image 1: Dark stripes with various orientations
on a uniform background.
Considering Eq. (10), by imposing two possible
orientations for A (135
◦
, 325
◦
) which corresponds to
the gradient orientations of the diagonal stripes, one
could expect to preserve them from isotropic diffu-
sion. Diffusion results are presented Fig. 6.
As one was expected it, the vertical and horizon-
tal dark stripes in diffused images tend to disappear
whereas the diagonal stripes are preserved all along
the diffusion process.
Let now consider a noisy simple grid diagonally
oriented corrupted by a Gaussian noise of standard
deviation set to 0.3.
If we apply the same diffusion process of Eq. (10)
to this noisy simple grid imposing this time four pos-
sible orientations for A corresponding to the four pos-
sible gradient orientations of the grid, it is then possi-
ble to show the denoising effect of the diffusion pro-
cess (Fig. 8).
(a) (b)
Figure 6: Diffusion of ”Image 1” (Fig. 5) for (a) n=100 and
(b) n=200. A. is chosen in order to preserve only diagonal
stripes from isotropic diffusion process. Time step τ is fixed
to 0.2.
Figure 7: Image 2: Noisy diagonally oriented grid (Gaus-
sian noise). PSNR (calculated with the non corrupted ver-
sion of the grid as reference) is equal to 68 dB.
(a) (b)
Figure 8: Diffusion of ”Image 2” (a) (Fig. 7) for (b) n=50.
As one can notice, the grid itself is preserved from the dif-
fusive effect of Eq. (3) whereas noise is iteration after iter-
ation removed. Time step τ is fixed to 0.2.
As intended, the grid itself is not diffused at all and
the increase of the Peak Signal to Noise Ratio (PSNR)
from 68 dB to 84 dB, shows that the added Gaussian
noise is removed iteration after iteration.
SELECTIVE IMAGE DIFFUSION FOR ORIENTED PATTERN EXTRACTION
273

4 DISCUSSION
In this article an original diffusion method, based on
the use of a particular PDE (Eq. (3)) derived from EPI
theory, has been presented. It has been shown that the
integration of the potential vector A within the formu-
lation of this PDE makes it possible the integration
within the diffusion scheme of particular constrains.
This has been assimilated to integration of selective-
ness within classical isotropic diffusion process. Ex-
amples on ad hoc images have been presented to show
the potential of the presented method in the areas of
denoising and extraction of oriented patterns.
Applications presented can be discussed, for fre-
quential filterings or Gabor-filters convolution can
lead to similar results. Considering that, it is neces-
sary to keep in mind that processed image have been
chosen in an ad hoc way to show the potential of the
method. Nevertheless, one major difference must be
noticed. Let consider again Fig. 5. If A is chosen
in order to preserve only one direction of the diago-
nal stripes, implementation of Eq. (3) leads to result
presented Fig. 9.
(a) (b)
Figure 9: Diffusion of ”Image 1” (Fig. 5) for (a) n=20 and
(b) n=50. As one can notice, Eq. (9) makes it possible to
only preserve one gradient direction of the diagonal stripes.
Time step τ is fixed to 0.2.
That kind of results can not be obtained by classi-
cal methods and enlarge the possible applications of
Eq. (3).
As a conlusion, an alternative method for oriented
pattern extraction has been presented in this article.
It has been demonstrated, as a proof a feasibility, on
ad hoc images that the developed approach may find
applicability in robotics and visions as far extraction
of oriented pattern is still an open problem. Indus-
trial control quality check can also be an other area of
applications.
REFERENCES
Alvarez, L., Guichard, F., Lions, P., and Morel, J. (1992).
Image selective smoothing and edge detection by non-
linear diffusion (ii). Arch. Rationnal Mech. Anal.,
29(3):845–866.
Catt
´
e, F., Coll, T., Lions, P., and Morel, J. (1992). Im-
age selective smoothing and edge detection by nonlin-
ear diffusion. SIAM Journal of Applied Mathematics,
29(1):182–193.
Courboulay, V., M
´
enard, M., Eboueya, M., and Courtelle-
mont, P. (2002). Une nouvelle approche du fil-
trage lin
´
eaire optimal dans le cadre de l’information
physique extreme. In RFIA 2002, pages 897–905.
Deriche, R. and Faugeras, O. (1996). Les edp en traitements
des images et visions par ordinateur. Traitement du
Signal, 13(6):551–578.
Fisher, R. (1922). Philosophical Transactions of the Royal
Society of London, 222:309.
Frieden, B. (1996). Fisher information as a measure of time.
Astrophysics and Space Sciences, 244:387–391.
Frieden, B. (1998). Physics from Fisher Information. Cam-
bridge University Press.
Geman, S. and Reynolds, G. (1992). Constrained restora-
tion and the recovery of discontinuities. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
14(3):367–383.
Nitzberg, M. and Shiota, T. (1992). Nonlinear image filter-
ing with edge and corner enhancement. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
14(8):826–833.
Nordstrom, N. (1990). Biased anisotropic diffusion-a uni-
fied regularization and diffusion approach to edge de-
tection. Image and Vision Computing, 8(4):318–327.
Perona, P. and Malik, J. (1990). Scale-space and edge
detection using anistropic diffusion. IEEE Transca-
tions on Pattern Analysis and Machine Intelligence,
12(7):629–639.
Terebes, R., Lavialle, O., Baylou, P., and Borda, M. (2002).
Mixed anisotropic diffusion. In Proceedings of the
16th International Conference on Pattern Recogni-
tion, volume 3, pages 1051–4651.
Tschumperle, D. and Deriche, R. (2002). Diffusion pdes on
vector-valued images. Signal Processing Magazine,
IEEE, 19:16–25.
Tschumperle, D. and Deriche, R. (2005). Vector-valued im-
age regularization with pde’s: A common framework
for different applications. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 27:506–517.
Weickert, J. (1995). Multiscale texture enhancement. In
Computer Analysis of Images and Patterns, pages
230–237.
Weickert, J. (1998). Anisotropic Diffusion in image process-
ing. Teubner-Verlag, Stuttgart.
Whitaker, R. and Pizer, S. (1993). A multi-scale approach to
nonuniform diffusion. CVGIP:Image Understanding,
57(1):99–110.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
274