FORMAL VERIFICATION OF SAFETY BEHAVIOURS OF THE

OUTDOOR ROBOT RAVON

Martin Proetzsch, Karsten Berns

Robotics Research Lab, University of Kaiserslautern, Germany

T. Schuele, K. Schneider

Reactive Systems Group, University of Kaiserslautern, Germany

Keywords:

Behaviour-based control, formal veriﬁcation, outdoor robotics.

Abstract:

This paper presents an approach to the formal veriﬁcation of safety properties of the behaviour-based control

network of the mobile outdoor robot RAVON. In particular, we consider behaviours that are used for the com-

putation of the projected vehicle’s velocity from obstacle proximity sensor data and inclination information.

We describe how this group of behaviours is implemented in the synchronous language Quartz in order to

be formally veriﬁed using model checking techniques of the Averest veriﬁcation framework. Moreover, by

integrating the automatically generated and veriﬁed code into the behaviour network, it can be guaranteed that

the robot slows down and stops as required by the given safety speciﬁcations.

1 INTRODUCTION

More and more applications like unmanned space

travelling, autonomous farming, civil protection, and

humanitarian demining require autonomous vehicles

navigating in unstructured natural terrain. The di-

versity as well as missing information for physical

models of outdoor scenarios call for a ﬂexible con-

trol architecture not requiring a complete knowledge

of the environment to achieve robust locomotion. In

this context, behaviour-based control networks have

proven suitable for appropriate reaction on external

inﬂuences.

One of the advantages of behaviour-based ar-

chitectures is emergence: The combination of be-

haviours leads to proper reactions not directly ex-

plainable by the individual components. On the other

hand, this feature also poses problems concerning

predictability, making it difﬁcult to reason about the

correctness of the overall system. However, safety

critical applications require proofs that guarantee that

given speciﬁcations are met. In particular, the correct-

ness of reactive control layers is mandatory for the ﬁ-

nal behaviour of the robot.

In circuit design, formal veriﬁcation has already

become a standard to avoid design errors. Since

all possible input traces of a system are considered

Figure 1: RAVON in rough outdoor terrain.

by formal veriﬁcation methods, it is guaranteed that

the checked speciﬁcations hold under all circum-

stances. In particular, different kinds of model check-

ing (Schneider, 2003; Schuele and Schneider, 2006)

are popular veriﬁcation methods due to the high de-

gree of automation.

In this paper, we consider the formal veriﬁca-

tion of a part of the behaviour-based control network

of the mobile outdoor platform RAVON (Robust

Autonomous Vehicle for Off-road Navigation, see

Fig. 1), namely RAVON’s control system that is re-

157

Proetzsch M., Berns K., Schuele T. and Schneider K. (2007).

FORMAL VERIFICATION OF SAFETY BEHAVIOURS OF THE OUTDOOR ROBOT RAVON.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 157-164

DOI: 10.5220/0001619101570164

 SciTePress

sponsible for slowing down and stopping the vehi-

cle. It is clear that this part is highly safety criti-

cal, and therefore, it is very important to guarantee

its correctness. To this end, we have implemented

this part of the behaviour-based control network in the

synchronous programming language Quartz (Schnei-

der, 2001b; Schneider, 2006). We then used the for-

mal veriﬁcation methods of the Averest framework

(Schneider and Schuele, 2005) to check the correct-

ness of our implementation with respect to given

safety conditions.

The application of formal methods to verify the

correctness of a robot system is not new: In (Diethers

et al., 2003), the model checker HyTech was used to

analyse a robot program based on skill primitive nets.

While HyTech considers hybrid automata as system

models to model continuous values of physical prop-

erties, our approach is based on discrete transition

systems that beneﬁt directly from symbolic model

checking techniques. The use of symbolic model

checking for the formal veriﬁcation of a robot sys-

tem has been reported in (Sharygina et al., 2004). In

contrast to our approach, however, the veriﬁcation is

not integrated with code generation.

The use of synchronous languages (Benveniste

et al., 2003) for the implementation of safety critical

control systems of robots is also not new: In (Sowmya

et al., 2002), a controller for a mobile robot (Rug

Warrior) has been implemented in the synchronous

language Esterel (Berry, 1998). In (Kim and Kang,

2005), the core of the Samsung Home Robot SHR100

has been re-engineered to be veriﬁed by means of

the Esterel framework. In contrast to our approach,

the systems considered in (Sowmya et al., 2002) and

(Kim and Kang, 2005) were quite small control pro-

grams with only a few control states.

In contrast to the previous work in this area, our

approach considers veriﬁcation as well as (veriﬁed)

code generation. Moreover, the considered system is

not simply a small control program, but a behaviour-

based control network with difﬁcult interdependen-

cies.

The outline of the paper is as follows: In the

next two sections, we give some details on the out-

door robot RAVON and its behaviour-based control

system. In Section 4, we describe the veriﬁcation

framework Averest and give some basics about syn-

chronous languages and model checking. Section 5

contains the results of the veriﬁcation. Finally, we

conclude with a summary and directions for future

work.

Figure 2: Regions monitored by the obstacle detection and

avoidance facilities.

2 THE OUTDOOR ROBOT

RAVON

RAVON is a four wheeled off-road vehicle measur-

ing 2.35 m in length and 1.4 m in width and weight-

ing 400kg. The vehicle features a four wheel drive

with independent motors yielding maximal velocities

of 3 m/s. In combination with its off-road tires, the

vehicle can climb slopes of 100% inclination predes-

tining it for the challenges in rough terrain. Front and

rear axis can be steered independently which supports

agile advanced driving manoeuvres like double Ack-

erman and parallel steering.

In order to navigate in a self-dependent fashion,

RAVON has been equipped with several sensors. For

self localisation purposes, the robot uses its odometry,

a custom design inertial measurement unit, a mag-

netic ﬁeld sensor, and a DGPS receiver. The sensor

data fusion is performed by a Kalman ﬁlter (Schmitz

et al., 2006) which calculates an estimated pose in

three dimensions. Due to gravity measurements of the

inertial measurement unit, the control system receives

quite precise absolute data for the roll and pitch angle

of the vehicle. These are fed into behaviours that are

responsible for supervising whether the vehicle might

tip over due to critical inclination.

In order to protect the vehicle in respect to ob-

stacles, several safety regions are observed by dif-

ferent sensor systems (Sch

afer and Berns, 2006) (see

Fig. 2). First of all, hindrances can be detected using

the stereo camera system mounted at the front of the

vehicle. The stereo camera’s narrow ﬁeld of vision

is compensated by local obstacle memories to either

side of the robot realising a short-term representation

of detected obstacles. This obstacle detection facility

is complemented with two laser range ﬁnders (ﬁeld

of vision: 180 degrees, angular resolution: 0.5 de-

grees, distance resolution: about 0.5 cm) monitoring

the environment nearby the vehicle. Data from both

sources of proximity data is used for obstacle avoid-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

158

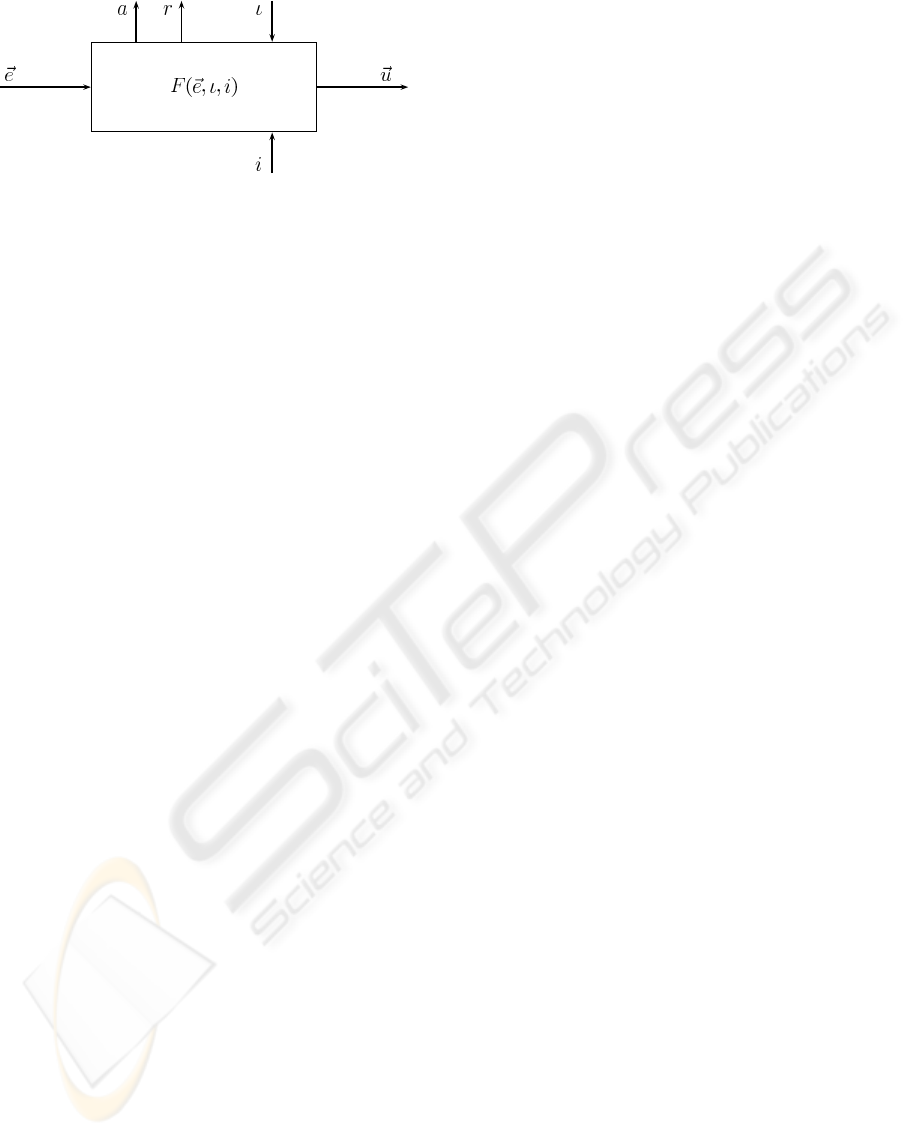
Figure 3: Basic behaviour module.

ance by appropriate behaviours, the fusion of which

is performed inside the behaviour network.In case of

emergency, the system is stopped on collision by the

safety bumpers which are directly connected to the

emergency stop to ensure maximal safety.

3 BEHAVIOUR-BASED

CONTROL SYSTEM OF RAVON

This section introduces the components used for

building up the behaviour-based network controlling

RAVON.

3.1 Behaviour Module

The fundamental unit of the proposed control archi-

tecture is the behaviour module (see Fig. 3). Each

atomic behaviour is wrapped into such a module with

a deﬁned interface. Behaviours can be described as

three-tuples of the form

B = (r,a,F) (1)

where r is the target rating function, a is the activ-

ity function, and F is the transfer function of the be-

haviour. Additionally each behaviour receives an in-

put vector ~e, an activation ι, and an inhibition i and

generates an output vector~u.

More precisely behaviours receive data needed for

fulﬁlling their work via the sensor input~e ∈ ℜ

which

can be composed of sensory data or information from

other behaviours. The output vector ~u ∈ ℜ

trans-

mits data generated by the behaviour. This output

describes the inﬂuence a behaviour can have on the

environment or on other behaviours.

Each behaviour owns an input determining its ac-

tivation ι ∈ [0, 1]. In this notation ι = 0 indicates de-

activation and ι = 1 a fully activated behaviour. Val-

ues between 0 and 1 refer to a partially activated be-

haviour. Activation can be used to adjust the rele-

vance of competing behaviours. The inverse effect is

achieved by inhibition i ∈ [0,1] which is used to re-

duce the activation of a behaviour: i = 1 refers to full

inhibition, i = 0 to no inhibition.

Information about the activity of a behaviour is

provided by the output a ∈ [0, 1]. The maximal ac-

tivity is described by a = 1, inactivity by a = 0. It is

deﬁned by the activity function

a(~e, ι,i) = a

int

(~e) · ι· (1− i) (2)

where a

int

(~e) ∈ [0, 1] is an internal function represent-

ing the intended activity of the behaviour.

The target rating r ∈ [0, 1] deals as an indicator

for the contentment of a behaviour. A value of r = 0

indicates that the behaviour is content with the actual

state, while r = 1 shows maximal dissatisfaction.

The output vector ~u of a behaviour is determined

using its transfer function F(~e,ι, i) where

F : ℜ

× [0,1]

→ ℜ

, F(~e,ι, i) = ~u

This function provides the intelligence of a behaviour,

calculating actions depending on input values and in-

ternal representations. This can be a reactive respond

to input values but also a more complex calculation

as a state machine or sophisticated algorithms. Both

reactive and deliberative behaviours can be imple-

mented that way.

3.2 Example Behaviour Roll Stop

In this section a behaviour reacting on high roll is de-

scribed in order to exemplify the behaviour properties

described before. As the behaviour wants to stop the

vehicle, the output ~u is a velocity of zero. Therefore

the transfer function is:

~u = v

out

= 0

This velocity has an effect if the activity a rises:

a =

Threshold

(

roll

) · ι· (1− i)

Here

Threshold

(

roll

) is a function returning 0 or 1

depending on the roll value being below or above a

given threshold. The activity is scaled by the activa-

tion ι and the inhibition i as stated above. Similarly

the target rating r is

r =

Threshold

(

roll

)

In case of normal roll angles the behaviour is con-

tent (r = 0) while for high roll angles it is dissatisﬁed

(r = 1).

3.3 Fusion Behaviour Module

In case of competing behaviours so called fusion be-

haviours (see ﬁgure 4) are used for coordination. The

underlying assumption of the fusion of output values

is that behaviours having a high activity deserve a

higher inﬂuence on the control than those with lower

FORMAL VERIFICATION OF SAFETY BEHAVIOURS OF THE OUTDOOR ROBOT RAVON

159

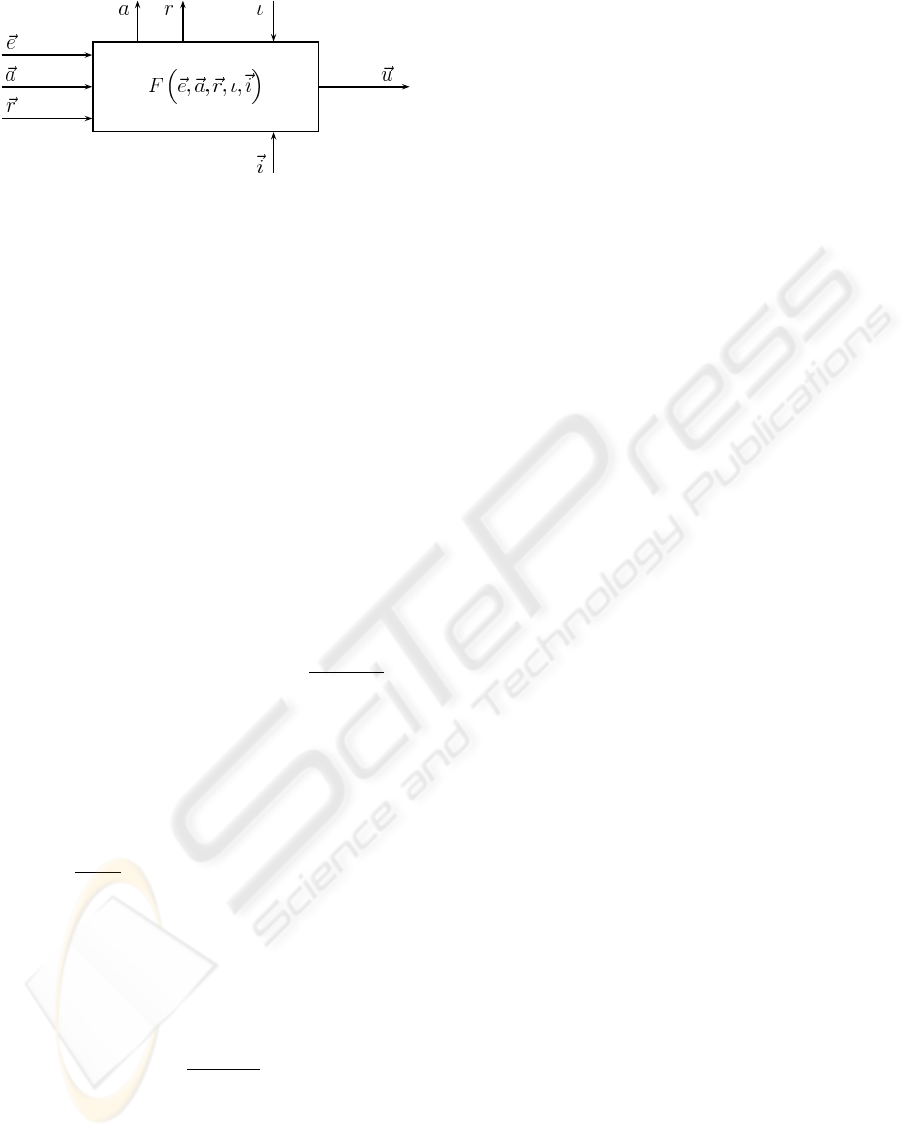
Figure 4: Fusion behaviour module.

activity. The interface of fusion behaviours imple-

ments a reﬁnement of usual behaviours. For each of

the competing behaviours

the activity (indicated by

~a), target rating (indicated by~r) and output vector~u is

provided. The output vector is fed into the fusion be-

haviour as~e. Additionally there is a fusion of inhibit-

ing behaviours by the inhibition inputs

i. The transfer

function then is the fusion function f(~a,~e) which pro-

cesses these input values to a merged output control

vector~u.

The fusion function can have several implementa-

tions, in this work the weighted fusion is used: Here

the control values are weighted with the activity of the

corresponding behaviour, leading to a fusion function

weighted

, where

~u = f

weighted

,~u

,. .. , a

n−1

,~u

n−1

) =

n−1

∑

j=0

·~u

n−1

∑

k=0

(3)

The activity is set according to the weighted input ac-

tivities, the activation, and the maximally activated in-

hibiting behaviour:

a =

n−1

∑

j=0

n−1

∑

k=0

· ι· (1− i

) where i

= max

)

The target rating of a fusion behaviour indicates its

goal to satisfy highly activated input behaviours and

is calculated as follows:

r =

n−1

∑

j=0

· r

n−1

∑

k=0

The weighted fusion function provides a subtle

gradation of coordinating behaviour control outputs

regarding their activity.

3.4 Behaviour Network of Ravon

The behaviour network implemented on RAVON is

shown in Fig. 5. Here the ﬂow of control data is

marked as blue drawn through line while data de-

rived from sensors as well as interpreted sensor data

(e.g. the activity output of behaviours used as inhi-

bition input for fusion behaviours) is marked as red

dashed line.

The behaviour network comprises three control

chains affecting desired rotation, sideward motion,

and velocity of the vehicle. The rotational and

the sideward components are inﬂuenced by obstacle

avoidance behaviours. For safety reasons the velocity

is adjusted according to obstacle proximity and criti-

cal vehicle inclination. In this behaviour network the

following types of behaviours are used:

• Emergency Stop: Stop due to laser scanner data,

positive or negative obstacles detected by the cam-

era system; independently used for forward and

backward motion.

• Slow Down: Reduce velocity due to obstacle

proximity (laser scanner, positive/negative obsta-

cles); independently used for forward and back-

ward motion.

• Keep Distance Rotational: Turn away from obsta-

cles (laser scanner, positive/negative obstacles);

independently used for both sides of the vehicle.

• Keep Distance Sideward: Accomplish sideward

motion due to obstacles at the side; independently

used for both sides of the vehicle.

• Evasion: Evade obstacles at the front by arbitrat-

ing between the keep distance behaviours.

• Point Access: Accessing a given position.

• Point Access Ranking: Perform ranking manoeu-

vres accounting for kinematic constraints.

• Trace Back: Follow just driven path backwards in

order to escape dead ends.

The advantage of this approach is the emergent

vehicle behaviour leading to unforeseen, but suitable

reaction on several external inﬂuences at a time. How-

ever, especially the maintenance of vehicle and person

safety requires methods for guaranteeing fundamental

characteristics of the vehicle motion e.g. in critical sit-

uations. Therefore, it is necessary to formally verify

the behaviour network with respect to a given set of

speciﬁcations.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

160

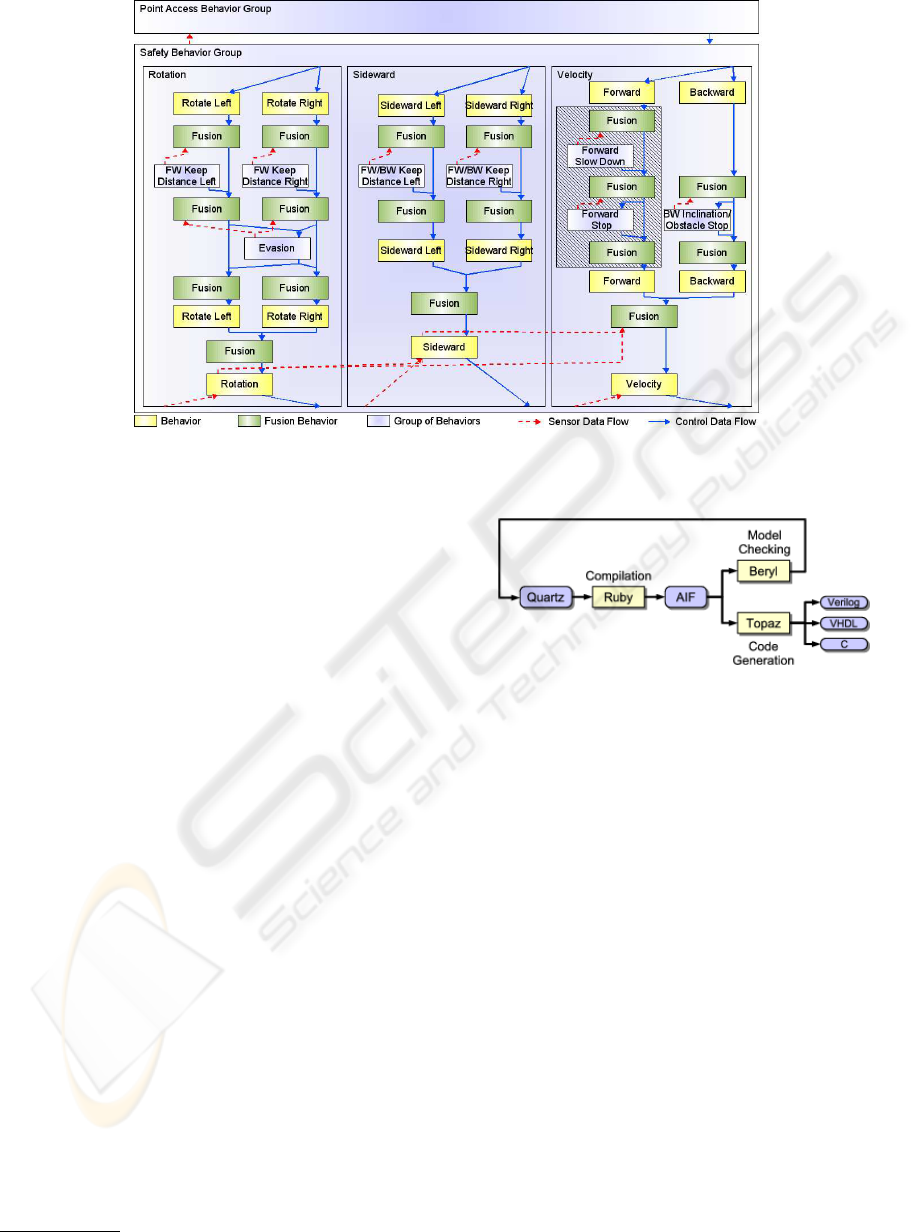
Figure 5: Behaviour network of RAVON.

4 THE AVEREST SYSTEM

In this section, we describe the Averest

frame-

work (Schneider and Schuele, 2005; Schneider and

Schuele, 2006) that provides tools for verifying

temporal properties of synchronous programs (Ben-

veniste et al., 2003; Halbwachs, 1993) as well as for

compiling these programs to equivalent hardware and

software systems. In particular, many formal veriﬁ-

cation techniques, including model checking of tem-

poral properties of ﬁnite and inﬁnite state systems

are available. In Averest, a system is described us-

ing the Esterel–like synchronous programming lan-

guage Quartz (Schneider, 2001a), and speciﬁcations

can be given in temporal logics such as LTL and CTL

(Schneider, 2003). Currently, Averest consists of the

following tools:

• ruby: a compiler for translating Quartz programs

to ﬁnite and inﬁnite state transition systems

• beryl: a symbolic model checker for ﬁnite and in-

ﬁnite state transition systems

• topaz: a code generator to convert transition sys-

tems into hardware and/or software

Figure 6 shows the typical design ﬂow. A given

Quartz program is ﬁrst translated to a symbolically

represented transition system in Averest’s Interchange

Format AIF that is based on XML. The AIF de-

scription can then be used for veriﬁcation and code

generation. Moreover, there are interfaces to third–

party tools, e.g. other model checkers such as SMV

http://www.averest.org

Figure 6: Averest design ﬂow.

(McMillan, 1992). In the remainder of this section,

we describe some background information on Averest

focusing on the veriﬁcation of behaviour networks.

The basic paradigm of synchronous languages

(Benveniste et al., 2003; Halbwachs, 1993) is the

distinction between micro and macro steps in a pro-

gram. From a programmer’s point of view, micro

steps do not take time, whereas macro steps take one

unit of time. Hence, consumption of time is explicitly

programmed by partitioning the program into macro

steps. This programming model, referred to as per-

fect synchrony (Benveniste et al., 2003; Halbwachs,

1993), together with a deterministic form of concur-

rency allows the compilation of multi–threaded syn-

chronous programs to deterministic single–threaded

code. A distinct feature of synchronous languages is

their detailed formal semantics that is usually given

by means of transition rules in structural operational

semantics. This makes synchronous languages attrac-

tive for safety–critical applications where formal ver-

iﬁcation is mandatory.

After translating a Quartz program to a transi-

tion system, it can be veriﬁed using symbolic model

FORMAL VERIFICATION OF SAFETY BEHAVIOURS OF THE OUTDOOR ROBOT RAVON

161

checking techniques. For that purpose, the speciﬁ-

cations are given as a set of temporal logic formulas

that describe the desired properties of the system. The

most frequently used properties are safety and live-

ness properties. Intuitively, a safety property states

that a condition invariantly holds on a given path of

the transition system. Similarly, a liveness property

states that a condition holds at least once on a given

path. As an example for a safety property, the formula

AGϕ states that ϕ holds on all possible computation

paths of the system. An example for a liveness prop-

erty is the formula EFϕ, stating that there exists a path

such that ϕ eventually holds.

A breakthrough in formal veriﬁcation was

achieved in the early nineties, where it was observed

that ﬁnite sets can be efﬁciently represented by means

of binary decision diagrams (BDDs), a canonical nor-

mal form for propositional logic formulas (Bryant,

1986). The development of BDDs was a cornerstone

for symbolic model checking procedures based on ﬁx-

point computations (Burch et al., 1990) (see textbooks

like (Clarke et al., 1999; Schneider, 2003) for more

details). With sophisticated implementations and re-

ﬁnements of symbolic model checking, it has become

possible to verify systems of industrial size, and to de-

tect errors that can hardly be found using simulation

(Clarke and Wing, 1996).

5 FORMAL VERIFICATION OF

THE BEHAVIOUR NETWORK

In case of RAVON, the most important behaviour

network property is the control of the vehicle ve-

locity due to obstacles or critical inclination. The

behaviours affecting the control in this respect are

marked hatched in Fig. 5. In order to formally verify

this part of the behaviour network, the correspond-

ing behaviours have been implemented in the syn-

chronous language Quartz. In this way, the correct-

ness of every single behaviour can be shown by means

of a symbolic model checker. By forming a group of

the mentioned behaviours, it is even possible to verify

speciﬁcations concerning the overall behaviour of the

complete velocity control part of the behaviour net-

work. Moreover, the Quartz code can be exported to

C code and can be wrapped into a module that re-

places the original (unveriﬁed) code. As the output of

the veriﬁed module is directly transferred to the vehi-

cle motion actuators, it can be guaranteed that slowing

down and stopping has the intended effect.

The veriﬁed and synthesized parts of RAVON’s

behaviour network are depicted in in Fig. 7. It shows

the following structure: If none of the slow-down and

Figure 7: Structure of the veriﬁed part of RAVON’s be-

haviour network.

stop behaviours is active, the velocity given by higher

layers (ci

velocity) is piped through the three fusion

behaviours without change to co

velocity. As soon as

one of the mentioned behaviours becomes active (in

case the inclination rises above a threshold or the ob-

stacle distance becomes too low), the active behaviour

uses its activity to inhibit the fusion behaviour which

is above it. At the same time, it proposes a velocity

of zero to the underlying fusion behaviour. This fu-

sion behaviour calculates a weighted sum (using the

input activities) of the input velocity values. The more

active a behaviour becomes, the less active the fu-

sion behaviour above is. Therefore, the inﬂuence of

the slow-down behaviour rises and the velocity output

of the underlying fusion behaviour decreases. This

mechanism is implemented on two layers here.

For this behaviour network, we checked eight

speciﬁcations including the ones we list below. In this

context, uppercase words indicate system parameters,

indicates controller inputs,

controller outputs,

and

sensor inputs. Numbers are marked as un-

signed integers (

• The output velocity is never higher than the input

velocity:

A G (co_velocity <= ci_velocity);

• In case of no near obstacle and tolerable inclina-

tion, the output velocity equals the input velocity.

Therefore, the vehicle is not slowed down without

a reason:

A G ((si_camera_distance

>= MAX_VELOCITY_OBSTACLE_DISTANCE)

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

162

& (si_scanner_distance

>= MAX_VELOCITY_OBSTACLE_DISTANCE)

& (si_roll

<= MAX_VELOCITY_INCLINATION)

& (si_pitch

<= MAX_VELOCITY_INCLINATION)

-> co_velocity == ci_velocity);

• If very high inclination or very near obstacles oc-

cur, the output velocity is set to zero, i.e., the ve-

hicle stops:

A G (si_roll >= STOP_INCLINATION

-> co_velocity == 0u);

A G (si_pitch >= STOP_INCLINATION

-> co_velocity == 0u);

A G (si_camera_distance

<= STOP_OBSTACLE_DISTANCE

-> co_velocity == 0u);

A G (si_scanner_distance

<= STOP_OBSTACLE_DISTANCE

-> co_velocity == 0u);

• In case of a rising roll angle, the vehicle slows

down. Similar speciﬁcations hold for the pitch an-

gle and for near obstacles:

A G (ci_velocity == MAX_VALUE

& si_camera_distance

> MIN_VELOCITY_OBSTACLE_DISTANCE

& si_scanner_distance

> MIN_VELOCITY_OBSTACLE_DISTANCE

& si_pitch

< MIN_VELOCITY_INCLINATION

& si_roll

> MAX_VELOCITY_INCLINATION

& si_roll

< MIN_VELOCITY_INCLINATION

-> co_velocity < MAX_VALUE

& co_velocity > 0u );

In order to avoid vacuous speciﬁcations, formulas of

the type AG(ϕ → ψ) are always complemented with

EFϕ (not shown here). In this way, it is guaranteed

that the antecedent of the implication is not always

false. All of our speciﬁcations can be expressed in

the temporal logic CTL. Hence, we can use state-

of-the-art model checking techniques to verify these

properties. Using global model checking, the model

checkers perform a complete traversal of the reach-

able states and thereby check whether the given speci-

ﬁcations hold. Using local model checking, the model

checkers perform some sort of an induction proof to

avoid a complete state space traversal.

BDD-based symbolic model checkers do usually

not support ﬂoating point numbers. Therefore, inte-

gers with a given bitwidth are used for the implemen-

tation in Quartz instead of ﬂoating point numbers. In

order to integrate the veriﬁed module in the control

system, a conversion from ﬂoating point to ﬁxpoint

numbers is performed for control and sensor values.

In our case study, global model checking was able

to check the speciﬁcations up to a sufﬁciently large

bitwidth. We used CadenceSMV as backend of Aver-

est. In the following table, we list experimental re-

sults for some bitwidths. For each bitwidth, we list

the number of reachable states, the runtime that was

necessary to verify the system, and the number of re-

quired BDD nodes for the entire veriﬁcation of the

eight speciﬁcations. All experiments were performed

on a PentiumIV with 512 MByte main memory.

Table 1: Experimental results of the veriﬁcation process.

bits states runtime (s) BDD nodes

3 1024 0.95 453

4 8192 1.59 10012

5 65536 2.54 10063

6 524288 3.87 10521

7 4194204 5.54 15399

8 33554432 8.85 49500

In the process of implementing the behaviour net-

work, the question arose if the fusion behaviours

could implement a maximum fusion function (i.e. the

most active behaviour has full inﬂuence) instead of

the weighted fusion function. By means of formal

veriﬁcation, it was possible to show that in this case

not all speciﬁcations were valid. Depending on the

implementation, there was either no slowing down of

the vehicle (but only abrupt stopping) or it was possi-

ble that the velocity output was higher than the veloc-

ity input. Experimental changes concerning the struc-

ture and implementation of the behaviour network

can therefore be performed with immediate feedback

about the correct properties stated in the speciﬁca-

tions.

6 CONCLUSIONS AND FUTURE

WORK

We presented an approach to the formal veriﬁcation of

a behaviour-based control network. Without the need

of testing, it is guaranteed that the speciﬁed proper-

ties are valid for all possible input traces. Of course,

it is necessary to verify more parts of the system or

even the complete behaviour-based network. Due to

the enormous number of states, this inevitably leads to

the need of improving the model checking approach.

Therefore, methods like modular model checking and

abstraction will have to be analysed in this respect.

The uniformity of the behaviours is seen to be an ad-

vantage in this context that can be exploited by tai-

lored veriﬁcation and abstraction techniques.

FORMAL VERIFICATION OF SAFETY BEHAVIOURS OF THE OUTDOOR ROBOT RAVON

163

ACKNOWLEDGEMENTS

The research work presented in this paper is funded

by the German Federal State of Rhineland-Palatinate

within the excellence cluster ”Dependable Adaptive

Systems and Mathematical Modeling”.

REFERENCES

Benveniste, A., Caspi, P., Edwards, S., Halbwachs, N., Le

Guernic, P., and de Simone, R. (2003). The syn-

chronous languages twelve years later. Proceedings

of the IEEE, 91(1):64–83.

Berry, G. (1998). The foundations of Esterel. In Plotkin, G.,

Stirling, C., and Tofte, M., editors, Proof, Language

and Interaction: Essays in Honour of Robin Milner.

MIT.

Bryant, R. (1986). Graph-based algorithms for Boolean

function manipulation. IEEE Transactions on Com-

puters, C-35(8):677–691.

Burch, J., Clarke, E., McMillan, K., Dill, D., and Hwang,

L. (1990). Symbolic model checking: 10

states and

beyond. In Symposium on Logic in Computer Science

(LICS), pages 1–33, Washington, D.C. IEEE Com-

puter Society.

Clarke, E., Grumberg, O., and Peled, D. (1999). Model

Checking. MIT, London, England.

Clarke, E. and Wing, J. (1996). Formal methods: State

of the art and future directions. Technical Report

CMU-CS-96-178, Carnegie Mellon University.

ftp://reports.adm.cs.cmu.edu/usr/anon/1996/CMU-

CS-96-178.ps.

Diethers, K., Firley, T., Krger, T., and Thomas, U. (2003).

A new framework for task oriented sensor based robot

programming and veriﬁcation. In International Con-

ference on Advanced Robotics (ICAR), pages 1208–

1214, Coimbra,Portugal. IEEE Computer Society.

Halbwachs, N. (1993). Synchronous programming of reac-

tive systems. Kluwer.

Kim, M. and Kang, K. (2005). Formal construction and

veriﬁcation of home service robots: A case study. In

Peled, D. and Tsay, Y.-K., editors, International Sym-

posium on Automated Technology for Veriﬁcation and

Analysis (ATVA), volume 3707 of LNCS, pages 429–

443, Taipei, Taiwan. Springer.

McMillan, K. (1992). The SMV system, symbolic model

checking - an approach. Technical Report CMU-CS-

92-131, Carnegie Mellon University.

Sch

afer, H. and Berns, K. (2006). Ravon - an autonomous

vehicle for risky intervention and surveillance. In In-

ternational Workshop on Robotics for risky interven-

tion and environmental surveillance - RISE.

Schmitz, N., Proetzsch, M., and Berns, K. (2006). Pose esti-

mation in rough terrain for the outdoor vehicle ravon.

In 37th International Symposium on Robotics (ISR).

Schneider, K. (2001a). Embedding imperative synchronous

languages in interactive theorem provers. In Confer-

ence on Application of Concurrency to System Design

(ACSD), pages 143–156, Newcastle upon Tyne, UK.

IEEE Computer Society.

Schneider, K. (2001b). Exploiting Hierarchies in Temporal

Logics, Finite Automata, Arithmetics, and µ-Calculus

for Efﬁciently Verifying Reactive Systems. Habilitation

Thesis. University of Karlsruhe.

Schneider, K. (2003). Veriﬁcation of Reactive Systems –

Formal Methods and Algorithms. Texts in Theoretical

Computer Science (EATCS Series). Springer.

Schneider, K. (2006). The synchronous programming lan-

guage Quartz. Internal Report (to appear), Department

of Computer Science, University of Kaiserslautern.

Schneider, K. and Schuele, T. (2005). Averest: Speciﬁca-

tion, veriﬁcation, and implementation of reactive sys-

tems. In Conference on Application of Concurrency

to System Design (ACSD), St. Malo, France. partici-

pant’s proceedings.

Schneider, K. and Schuele, T. (2006). A framework for

verifying and implementing embedded systems. In

Straube, B. and Freibothe, M., editors, Methoden und

Beschreibungssprachen zur Modellierung und Veri-

ﬁkation von Schaltungen und Systemen, pages 242–

247, Dresden, Germany. GI/ITG/GMM, Fraunhofer

Institut fr Integrierte Schaltungen, ISBN 3-9810287-

1-6.

Schuele, T. and Schneider, K. (2006). Bounded model

checking for inﬁnite state systems. Formal Methods

in System Design (FMSD). DOI 10.1007/s10703-006-

0019-9.

Sharygina, N., Browne, J., Xie, F., Kurshan, R., and Levin,

V. (2004). Lessons learned from model checking a

NASA robot controller. Formal Methods in System

Design (FMSD), 25(2-3):241–270.

Sowmya, A., So, D., and Tang, W. (2002). Design of a mo-

bile robot controller using Esterel tools. Electronic

Notes in Theoretical Computer Science (ENTCS),

65(5). Workshop on Synchronous Languages, Appli-

cations, and Programming (SLAP).

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

164