TAKAGI-SUGENO MULTIPLE-MODEL CONTROLLER FOR A
CONTINUOUS BAKING YEAST FERMENTATION PROCESS
Enrique Herrera
1
, Bernardino Castillo
Centro de investigación y de Estudios Avanzados del I.P.N., Unidad Guadalajara, Av. Científica 1145, Colonia el bajío
C.P. 45010, Zapopan, México
Jesús Ramírez
Centro de Investigación y Asistencia en Tecnología y Diseño del Estado de Jalisco A.C., Av. Normalistas 800
C.P. 44270, Guadalajara, México
Eugénio C. Ferreira
IBB-Institute for Biotechnology and Bioengineering, Centre of Biological Engineering, Universidade do Minho
4710-057, Braga, Portugal
Keywords: Nonlinear system, Fuzzy model, Fuzzy controller, Fermentation process.
Abstract: The purpose of this work is to design a fuzzy integral controller to force the switching of a bioprocess
between two different metabolic states. A continuous baking yeast culture is divided in two sub-models: a
respiro-fermentative with ethanol production and a respirative with ethanol consumption. The switching
between both different metabolic states is achieved by means of tracking a reference substrate signal. A
substrate fuzzy integral controller model using sector nonlinearity was built for both nonlinear models.
1 INTRODUCTION
Control applications in bioprocesses have increased
in the last decades due to the fast advances on
computer and electronic technology. An adequate
control of fermentation processes allows reducing
production costs and increases the yield, while at the
same time achieving the quality of the desired
product (Yamuna and Ramachandra 1990).
In the case where the nonlinear model of the
process is known, a fuzzy system may be used. A
first approach can be done using the Takagi-Sugeno
(TS) fuzzy model, (Takagi and Sugeno, 1985),
where the consequent part of the fuzzy rules are
replaced by linear systems. This can be attained, for
example, using the method of sector nonlinearities
_________________________
1
On Ph. D. studies leave from the Centro de Investigación
y Asistencia en Tecnología y Diseño del Estado de Jalisco.
which allows constructing an exact fuzzy model
from the original nonlinear system by means of
linear subsystems (Tanaka and Wang, 2001). From
this exact model a controller may be designed based
on the linear subsystems.
Along this line of reasoning, in this work a fuzzy
integral controller based on sector nonlinearities is
proposed and applied to a continuous baker’s yeast
process. An interesting feature of this model is the
splitting in two different partial models: a respiro-
fermentative (RF) model with ethanol production
and the respirative (R) model with ethanol
consumption. The fuzzy integral controller is used to
force the switching of a bioprocess between both
different metabolic states by means of tracking a
reference substrate signal.
436
Herrera E., Castillo B., Ramírez J. and C. Ferreira E. (2007).
TAKAGI-SUGENO MULTIPLE-MODEL CONTROLLER FOR A CONTINUOUS BAKING YEAST FERMENTATION PROCESS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 436-439
DOI: 10.5220/0001622704360439
Copyright
c
 SciTePress

2 FUZZY MODELS BASICS
2.1 Takagi-Sugeno Fuzzy Model
The Takagi-Sugeno fuzzy models are used to
represent nonlinear dynamics by means of a set of
IF-THEN rules. The consequent parts of the rules
are local linear systems. The ith rule of a continuous
fuzzy model has the following form:
11
() () ()
( ) ( ) 1 ,
ii
pp
ii
i
IF z (t) is M and...and z (t) is M
xt Axt But
THEN
y t C x t i ,...,r
=+
⎧
⎨
==
⎩

(1)
where
i
j
M
is a fuzzy set and r is the number of rules
in the fuzzy model; x(t)
∈ R
n
is the state vector, u(t)
∈ R
m
is the input vector, y(t) ∈ R
q
is the output
vector, A
i
∈ R
nxn
, B
i
∈ R
nxm
, y C
i
∈ R
qxn
are suitable
matrices and z(t)=[z
1
(t),…,z
p
(t)] is a known vector of
premise variables which may depend partially on the
state x(t). Given a pair of (x(t), u(t)) and a product
inference engine the aggregate TS fuzzy model can
be inferred as:
{}
1
1
() ( ()) () (),
() ( ()) (),
r
iii
i
r
ii
i
x
thztAxtBut
yt h zt Cxt
=
=
=+
=
∑
∑

(2)
where
1
11
( ( )) ( ( )) ( ( )) ,
pp
r
ii
ijj jj
i
jj
hzt M z t M z t
=
==
⎛⎞
=
⎜⎟
⎝⎠
∑
∏∏
for all t. The term
))(( tzM
j
i
j
is the membership
value of z
j
(t) in
i
j
M
. We have that
(()) 0
i
hzt ≥
and
1
(()) 1
r
i
i
hzt
=
=
∑
for all t and i=1,…,r.
2.2 Parallel Distributed Compensator
The parallel distributed compensator (PDC) is used
to design a fuzzy controller from a TS fuzzy model.
Each control rule is designed from the corresponding
rule of a TS model.
11
ii
p
p
I
F z (t) is M and...and z (t) is M
1
( ) ( ( )) ( ) 1 ,
r
ii
i
THEN u t h z t F x t i ,...,r
=
=− =
∑
(3)
where F
i
is the controller gain for the ith subsystem,
which makes Hurwitz the matrices A
i
-B
i
F
i
.
2.3 Integral Control
Consider the linear system
() () () ()
R
tAtButyt
ξξξ
ξξ =+ +

,
(4)
where
,
ξ

ξ, A
ξ
, B
ξ
, u
ξ
(t) and y
R
are given by
()
x
t ξ
σ
⎡
⎤
=
⎢
⎥
⎣
⎦



,
()
x
t ξ
σ
⎡
⎤
=
⎢
⎥
⎣
⎦
,
0
0
A
A
C
ξ
⎡⎤
=
⎢⎥
−
⎣⎦
,
0
B
B
ξ
⎡
⎤
=
⎢
⎥
⎣
⎦
,
0
()
R
R
yt
y
⎡
⎤
=
⎢
⎥
⎣
⎦
, u
ξ
(t)= -Fx + kσ
where
R
ey y
σ
=
=−

is a tracking error and y
R
(t) is
a reference signal. It is desired to design a state
feedback control such that y(t)→y
R
(t) as t→∞
(Khalil, 1996). If the pair (A,B) is controllable and
the following condition is achieved
0
AB
rank n p
C
⎡⎤
=
+
⎢⎥
−
⎣⎦
,
(5)
then it is possible to find a matrix K such that A
ξ
-B
ξ
K
is Hurwitz, assuring that y(t) - y
R
(t)→0 as t→∞;
where K=[-F, k] and k must be nonsingular.
3 THE EXACT FUZZY
CONTROLLER
A continuous baking yeast culture may be
represented by the following nonlinear system
))(()())(()( txdtButxftx
i
+
+
=

where
))(( txf
i
describes a respiro-fermentative baking yeast partial
model (RF) with ethanol production and a
respirative baking yeast partial model (R) with
ethanol consumption (Pormeleau, 1990). The RF
partial model is described by
RF model
1
1
1
max max
241
2
42
1
max max
2
41
12 2 2
2
42
3
max max
2
41
33
4
42
max
4
52
4
00
00
00
000
O
oOr rs
O
O
oOr rs
O
RF
O
ro rs
O
Oo
Y
xx
qYY Yq
Ko x Y Ks x
x
Y
xx
qkYkY kYq
x
Ko x Y Ks x
f
x
Y
xx
kYq kYq
x
YKox Ksx
x
kY q
Ko x
⎡⎤
⎛⎞
−
⎢⎥
⎜⎟
++
⎝⎠
⎢⎥
⎢⎥
⎛⎞
⎢⎥
−+ −
⎜⎟
⎢⎥
++
⎝⎠
=
⎢⎥
⎢⎥
−
⎢⎥
++
⎢⎥
⎢⎥
−
⎢⎥
+
⎣⎦
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
(6)
TAKAGI-SUGENO MULTIPLE-MODEL CONTROLLER FOR A CONTINUOUS BAKING YEAST FERMENTATION
PROCESS
437

The R model can be divided in two sub models
(Ferreira, 1995):
Rqe1 model
max max
3
1
32 2
max 1
1
1
2
2
1
max
3
3
4
32
4
max max
1
65
32 2
00
()()
000
000
()()
3
00
()()
ee Os
Os
Rqe
ee
ee Os
x
x
Yq Ki Y q
Ke x Ki x Ks x
x
x
kY q
Ks x
x
f
x
x
kYq Ki
Ke x Ki x
x
xx
kYq Ki kYq
Ke x Ki x Ks x
⎡⎤
⎢⎥
++ +
⎢⎥
⎢⎥
⎡
⎤
−
⎢⎥
⎢
⎥
+
⎢⎥
⎢
⎥
=
⎢⎥
⎢
⎥
−
⎢⎥
⎢
⎥
++
⎣
⎦
⎢⎥
⎢⎥
−−
⎢⎥
++ +
⎣⎦
(7)
Rqe2 model
max max
41
22
42 2
max
1
1
2
2
max max
41
42 42
422
max max
41
62 5 62
42 2
00
000
00
00
O
Oo s O O
O
Os
Rqe
O
Oo Os
O
O
Oo s O O
O
Y
xx
Yeq q Y Ye
Ko x Ks x Y
x
kY q
Ks x
f
Yxx
kY eq kY eq
Ko x Ks x Y
Yxx
kY eq q kY kY e
Ko x Ks x Y
⎡⎤
⎛⎞
−
⎢⎥
⎜⎟
++
⎝⎠
⎢⎥
⎢⎥
−
⎢⎥
+
⎢⎥
=
⎢⎥
⎢⎥
−
++
⎢⎥
⎢⎥
⎛⎞
⎢⎥
−−+
⎜⎟
⎢⎥
++
⎝⎠
⎣⎦
1
2
3
4
x
x
x
x
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
(8)
The input B matrix for all the models is given by
12 34
[, , , ]
T
in
B
xxS xx=− − + − −
(9)
where x
1
is the biomass, x
2
is the substrate, x
3
is the
ethanol, x
4
is the dissolved oxygen, S
in
is the inlet
substrate concentration, D is the dilution rate,
u(t)=D. The yield coefficients k
1
to k
6
and the
remaining parameters values are described in
Ferreira, (1995). The oxygen transfer rate (OTR) is
assumed to be a measurable and known perturbation,
and thus d=[0 0 0 OTR]
T
. Before designing a fuzzy
controller an exact fuzzy model must be first built.
When the nonlinear dynamic model for the
baking yeast is known, as well as all their
parameters, a fuzzy exact model can be derived from
the given nonlinear model. This requires a sector
nonlinearity approach (Tanaka and Wang, 2001).
From the models (6-9) the fuzzy exact model can be
constructed. The premise variables for the RF partial
model (6) and the input B matrix (9) are chosen as:
4
4
1
)(
xKo
x
tz
+
=
2
1
2
)(
xKs
x
tz
+
=
12 3 4
123 4
() , () , () , () .
xx x x
z
txztxztxztx=== =
The membership functions can be obtained from
2
1
() ( ())
ii
i
zt M zt a
=
=
∑
where the following property
12
(()) (()) 1Mzt Mzt+=
must be accomplished
(Tanaka and Wang , 2001). The linear subsystems
,
R
FRF
ijklmn ijklmn
AB
are derived from
max max
2
2
1
max max
2
12 2 2
2
3
max max
2
4
33
max
52
00
00
00
000
O
oOr rs
O
O
oOr rs
RF
ijklmn
O
O
ro rs
O
Oo
Y
qYY Yq
Y
x
Y
qkYkY kYq
x
A
Y
x
Y
x
kYq kYq
Y
kYq
ab
ij
ab
ij
ab
ij
a
i
⎡⎤
⎛⎞
−
⎢⎥
⎜⎟
⎝⎠
⎢⎥
⎡⎤
⎢⎥
⎛⎞
⎢⎥
⎢⎥
−+ −
⎜⎟
⎢⎥
⎢⎥
=
⎝⎠
⎢⎥
⎢⎥
⎢⎥
⎢⎥
−
⎣⎦
⎢⎥
⎢⎥
−
⎢⎥
⎣⎦
[
]
, , ,
T
RF
ijklmn k l in m n
BcdSef=− − + − −
(10)
i,j,k,l,m,n = 1,2.
where a
i
, b
j
, c
k
, d
l
, e
m
, f
n
are the maximum and
minimum values of z
1
(t), z
2
(t), z
x1
(t), z
x2
(t), z
x3
(t) and
z
x4
(t) respectively. The following ranges for x
1
(t) ∈ [0,
10], x
2
(t) ∈ [0, 1], x
3
(t) ∈ [0, 5] and x
4
(t) ∈ [0, 0.007]
were assumed.
From the model (10) the substrate integral
controller for the RF partial model can be designed
using the following model:
[]
max
2
2
0
10
,
RF
sj
j
T
RF
llin
x
kYrq b
A
BdS
σ
⎡⎤
−
⎡⎤
=
⎢⎥
⎢⎥
−
⎣⎦
⎣⎦
=− +
(11)
From models (10) and (11) the
,
R
FRF
ijklmn ijklmn
AB
matrices for the RF partial integral PDC
can be written as
max max
2
2
1
max max
2
12 2 2
2
3
max max
2
33 4
max
52
000
000
000
0 000
0 1 000
O
oOr rs
O
O
oOr rs
O
RF
ijklmn
O
ro rs
O
Oo
Y
qYY Yq
Y
x
Y
qkYkY kYq
x
Y
A
x
Y
kYq kYq x
Y
kYq
ab
ij
ab
ij
ab
ij
a
i
σ
⎡⎤
⎛⎞
−
⎢⎥
⎜⎟
⎝⎠
⎢⎥
⎡⎤
⎢⎥
⎛⎞
⎢⎥
⎢⎥
−+ −
⎜⎟
⎢⎥
⎢⎥
⎝⎠
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
−
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
−
⎢⎥
⎢⎥
−
⎣⎦
[
]
, , , , 0
T
RF
ijklmn k l in m n
BcdSef=− − + − −
(12)
i,j,k,l,m,n = 1,2.
A general fuzzy rule to infer all the fuzzy rules
for the RF PDC can be stated as:
IF z
1
(t) is “M
1i
(z
1
(t))” and z
2
(t) is “M
2j
(z
2
(t))” and
zx1(t) is “M
3k
(z
x1
(t))” and z
x2
(t) is “M
4l
(z
x2
(t))” and
z
x3
(t) is “M
5m
(z
x3
(t))” and z
x4
(t) is “M
6n
(z
x4
(t))”
() ()
RF
ijklmn
THEN u t F x t=−
(13)
From (12) and using the notation given by (4)
the aggregated fuzzy controller for the RF partial
model turns to be
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
438

{}
64
1
() ( ()) () () ,
RF RF RF
ijklmn ijklmn ijklmn R
x
thztABF tytd
ψ
ξ
⎡⎤
=−++
⎣⎦
∑

(14)
where
2( 1) 4( 1) 8( 1)
16( 1) 32( 1),
nm l k
ji
ψ
=+ −+ −+ −
+−+−
1
234
11 2 2 3
45 6
( ( )) ( ( )) ( ( )) ( ( ))
( ( )) ( ( )) ( ( ))
ijkx
lx mx nx
hzt M ztM ztM zt
M
ztM ztM zt
ψ
=
×
(15)
It has to be noticed that x
1
, x
3
and x
4
are not
taken into account in the PDC design; this is because
these states are not intended to be stabilized but to
switch between the RF and R partial models. The
fuzzy controller for the models Rqe1 and Rqe2 were
constructed following the same procedure.
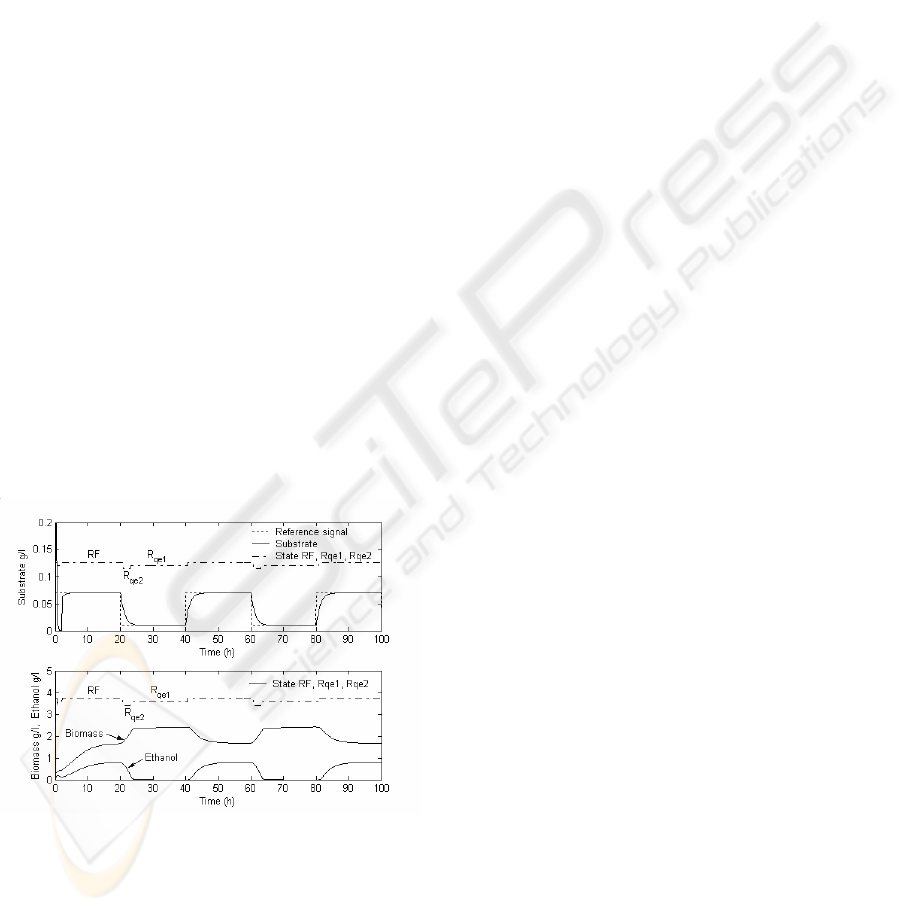
4 SIMULATION RESULTS
The application of the proposed controller scheme
was simulated using MATLAB™. In order to force
the switching between the RF and the R baking yeast
partial models, the substrate fuzzy controller was
forced to track a square reference signal, varied
between 0.01 g/l and 0.07 g/l. S
in
was set to 5 g/l.
The behavior of the substrate fuzzy tracking
controller as well as the biomass and ethanol
behavior are shown in figure 1.
Figure 1: Fuzzy controller performance and biomass and
ethanol behavior.
It can be notice that on the RF model, ethanol is
produced, limiting the biomass growth; when the
Rqe2 partial model is enable the ethanol is
consumed promoting biomass growth, and on the
Rqe1 state partial model the ethanol is consumed
and the biomass is growing just due to the substrate
uptake. To test the fuzzy integral controller
performance, it was enabled when 2 hours of
fermentation elapsed time was accomplished.
5 CONCLUSIONS
Based on the idea of splitting a continuous baking
yeast model, a TS fuzzy model was proposed using
the sector nonlinearities method, giving an exact
representation of the original nonlinear plant.
Moreover, a controller for each partial model was
constructed. It is worth noting that the controller was
capable to force the switching along the partial
models. Therefore, the approach presented here may
be considered a valid method to design a controller.
ACKNOWLEDGEMENTS
This paper has been supported by the Mexican
Consejo Nacional de Ciencia y Tecnología
(CONACyT), under grants 46538, 41148 and the
Ph.D. Schoolarship 70662.
REFERENCES
Ferreira, E., 1995. Identificação e controlo adaptivo de
processos biotecnológicos. Ph. D Thesis, Universidade
do Porto, Portugal.
Khalil, H. 1996. Nonlinear Systems, second edition.
Prentice Hall. United States of America.
Pormeleau, Y., 1990. Modelisation et controle d’un
procéde fed-batch de culture des levures á pain
(saccharomyces cerevisiae). Ph. D. Thesis. Ecole
Polytechnique de Montréal, Canada.
Takagi, T., Sugeno, M., 1985. Fuzzy identification of
systems and its applications to modelling and control.
IEEE Trans. Sys, Man Cyber, 15, 116-132.
Tanaka, K., Wang, H., 2001. Fuzzy control systems
design and analysis, a linear matrix inequality
approach. John Wiley & Sons, United States of
America.
Yamuna, R., Ramachandra, R., 1999. Control of
fermenters - a review. Bioprocess Engineering, 21, 77-
88.
TAKAGI-SUGENO MULTIPLE-MODEL CONTROLLER FOR A CONTINUOUS BAKING YEAST FERMENTATION
PROCESS
439