
ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER
DESCRIPTORS
E. González, V. Feliú, A. Adán* and Luis Sánchez**
H.T.S. of Industrial Engineering, University of Castilla La Mancha, Ave. Camilo José Cela s/n
Ciudad Real, 13071, Spain
*Higher School of Informatics,Universit
y of Castilla La Mancha, Ronda de Calatrava 5
Ciudad Real, 13071, Spain
**U.E of Technical Industria
l Engineering,University of Castilla La Mancha, Ave Carlos III, s/ n
Toledo, 45071, Spain
Keywords: Active recognition system, nex
t best view, silhouette shape, Fourier descriptors.
Abstract: This paper presents a new 3D object recognition/pose strateg
y based on reduced sets of Fourier descriptors
on silhouettes. The method consists of two parts. First, an off-line process calculates and stores a clustered
Fourier descriptors database corresponding to the silhouettes of the synthetic model of the object viewed
from multiple viewpoints. Next, an on-line process solves the recognition/pose problem for an object that is
sensed by a real camera placed at the end of a robotic arm. The method avoids ambiguity problems (object
symmetries or similar projections belonging to different objects) and erroneous results by taking additional
views which are selected through an original next best view (NBV) algorithm. The method provides, in very
reduced computation time, the object identification and pose of the object. A validation test of this method
has been carried out in our lab yielding excellent results.
1 INTRODUCTION
Most computer vision systems used in robotics
environments perform 3D object recognition tasks
using a single view of the scene (Bustos et al.,
2005). Commonly, a set of features is extracted and
matched with features belonging to an object
database. This is why so many researchers focus
their recognition strategy on finding features which
are capable of discriminating objects efficiently
(Helmer and Lowe, 2004). However, these
approaches may fail in many circumstances due to
the fact that a single 2D image may be insufficient.
For instance, this happens when there are objects
that are very similar from certain viewpoints in the
database (ambiguous objects); a difficulty that is
compounded when we have large object databases
(Deinzer et al., 2003).
A well known strategy that solves the ambiguity
pr
oblem is based on using multiple views of the
object. Active recognition systems provide the
framework to efficiently collect views until the
sufficient level of information for developing the
identification and posing estimation tasks is obtained
(Niku, 2001).
Previous works on active recognition differ in
the way they
represent objects, the way they
combine information and the way of they plan the
next observation (Roy et al., 2004). These systems
use 3D representation schemes based on the object
geometric model or on the object appearance.
Although X recognition based on geometric models
might be potentially more effective and allow for the
identification of objects in any position, they raise
important problems of practical aplicability.
Moreover, the methods based on X appearance are
currently the most successful approaches for dealing
with 3D recognition of arbitrary objects.
Many strategies for solving the 3D object
recogn
ition problem using multiple views have been
proposed: an aspect graph is used in Hutchinson and
Kak (1992) to represent the objects. This criterion
handles a set of current hypotheses about the object
identity and position. It characterizes the recognition
ambiguity by an entropy measure (Dempster-Shafer
theory) and evaluates the next best sensing operation
by minimizing this ambiguity. Borotsching et al.
318
González E., Feliú V., Adán A. and Sánchez L. (2007).
ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 318-325
DOI: 10.5220/0001627003180325
Copyright
c
SciTePress

(1999) represent the objects by some appearance-
based information, namely the parametric
eigenspace. This representation is augmented by
adding some probability distributions. These
probability distributions are then used to provide a
gauge for performing the view planning. Sipe and
Casasent (2002) use a probabilistic extension of the
feature space trajectory (FST) in a global eigenspace
to represent 3D views of an object. View planning is
accomplished by determining - for each pair of
objects – the most discriminating view point in an
off-line training stage. Their approach assumes that
the cost of making a mistake is higher than the cost
of moving the sensor.
In general, most of these approaches solve the
3D object recognition problem using stochastic or
probabilistic models and, consequently, they require
a large dataset for training (Deinzer et al., 2006).
Here we present a different way to focus on the
problem.
The key to our active recognition system consists
of using a reduced set of Fourier descriptors to
connect and develop the recognition phases: object
representation, classification, identification, pose
estimation and next best view planning.
We focus the object representation on silhouettes
because: they can be robustly extracted from
images, they are insensitive to surface feature
variations - such as color and texture - and, finally,
they easily encode the shape information (Pope et
al. 2005). The most popular methods for 2D object
recognition from silhouettes are based on invariant
moments or Fourier descriptors. Invariant moments
exhibit the drawback that two completely different
silhouettes may have the same low order invariant
moments, which may lead to ambiguities in the
recognition process. Fourier descriptors yield much
more information about the silhouette, and only
similar silhouettes exhibit similar Fourier
descriptors. Since we consider the objects to be non-
occluded and the background to be uncluttered, we
use a representation scheme in which the silhouettes
from different viewpoints are represented by their
Fourier descriptors.
This paper is organized as follows. Section 2
presents an overview of the method. Section 3
describes our object identification/pose estimation
approach. Section 4 details the next best view
method. Section 5 shows the performance of our
method by carrying out experiments on a real
platform, and some conclusions are stated in Section
6.
2 OVERVIEW OF THE METHOD
In this method the scene silhouette (silhouette of the
3D object to be recognized) is recognized among a
set of silhouettes (in our case, 80 or 320 per object)
of a group of objects through an algorithm based on
Fourier descriptors. Therefore, X recognition of the
silhouette of the scene involves both object
identification and pose. The method consists of off-
line and on-line parts.
The off-line process consists of building a
structured database of silhouettes belonging to a
generic set of objects. Firstly, a high precision three-
dimensional model of each object is obtained by
means of a laser scanner sensor. Next, this model is
viewed from a set of homogeneous viewpoints
obtaining the corresponding set of 2D silhouettes.
The viewpoints correspond to the vertexes of a
tessellated sphere with origin in the centre of mass
of the object. Figure 1 shows an object model inside
the tessellated sphere, the projected image of the
model and its silhouette from a specific viewpoint.
a)
b)
c)
d)
Figure 1: a) Object model put into the tessellated sphere b)
View of the object model from a specific viewpoint, c)
Depth image d) 2D silhouette.
The database is structured in clusters using only
three Fourier descriptors. To build the clustering we
used a k-means algorithm (Netanyahu et al., 2002).
This strategy allows us to split the silhouette search
space in zones where the silhouettes are roughly
similar. Consequently, the cost of the recognition
process is dramatically reduced. Figure 2 a) shows
the most important Fourier descriptors modules for a
couple of silhouettes. In our case, we have taken the
second, third and next to the last values. Figure 2 b)
presents the reconstructed silhouette with the three
Fourier descriptors superimposed on the original
one. Note that by selecting the most meaningful
Fourier components it is possible to work with
approximate shapes. Figure 3 shows a spatial
ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS
319

representation of the clusters that have been
extracted in our database.
The on-line process is designed to solve the
recognition/pose problem of an object that is viewed
by a camera in a real environment. The essential
steps are: Fourier descriptor calculation,
classification (discrimination) process,
identification/pose calculation and next view
algorithm. Next, a brief explanation of these steps is
provided.
a)
b)
Figure 2: a) Fourier descriptors modules b) silhouette (red)
and silhouette recovered with three Fourier descriptors
(blue).
To calculate the Fourier descriptors a suitable
image preprocessing is carried out on the original
image. Specifically this process consists of filtering,
thresholding and contour extraction. Next the points
of the contour are taken as a sequence of complex
numbers and the Fourier descriptors are finally
computed.
The discrimination phase classifies the silhouette
of the scene into a single or a set of clusters. The
selected clusters constitute the work sub-space in the
pose phase. Formally,
Let a database of N objects, C
...O ,O,O
N21
k
the
kth cluster, k ∈ [1..K], the n-th silhouette of
the object m, the k-th cluster prototype, D the
Euclidean distance, the k-th cluster radius where
and z the silhouette of the
scene to be matched. The subspace will be
formed by the clusters, which verify one or both of
the following conditions:
S
nm
k
k
p
k
R
) S,D(pmax R
nm
kkk
=
sub
S
Criterion 1: If
subkkk
SCthenRzpD ∈<),(
Criterion 2:
If
[1..K] i ,S C then |minD - D·|
subiki
∈∈
<
ε
The criterion 1 is satisfied for cases where z is
inside a cluster whereas criterion 2 corresponds to
cases where the silhouette z is inside an area with
very high cluster density or where the scene
silhouette falls outside the clusters. Thus, the
discrimination process sets a work subspace
with a reduced database of silhouettes.
sub
S
The identification phase, which is carried out
in , yields, in general, a reduced set of candidate
silhouettes. The reason for taking only a few
candidates is as follows. Matching and alignment
techniques based on contour representations are
usually effective in 2D environments. Nevertheless,
in 3D environments these techniques have serious
limitations. The main problems with the contour
based techniques occur due to the fact that the
information on the silhouettes may be insufficient
and ambiguous. Thus, similar silhouettes might
correspond to different objects from different
viewpoints. Consequently, a representation based on
the object contour may be ambiguous, especially
when occlusion circumstances occur.
sub
S
In essence, the identification phase compares the
silhouette from the scene with the silhouettes in the
subspace by means a quadratic error
minimization applied on the modulus of the Fourier
descriptors. If the identification/pose process
proposes more than one candidate silhouette, then
the solution is ambiguous and it is necessary to
apply the Next Best View planning method (NBV).
Figure 4 shows a scheme with the main process.
sub
S
Figure 3: Spatial representation of the silhouette clusters.
In most cases, the recognition and pose estimation
phase is finished after several views of the object are
taken and only one candidate is found. In this
process, the position of the next view is calculated
through an algorithm based on the set of candidate
silhouettes obtained in the previous view. This will
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
320
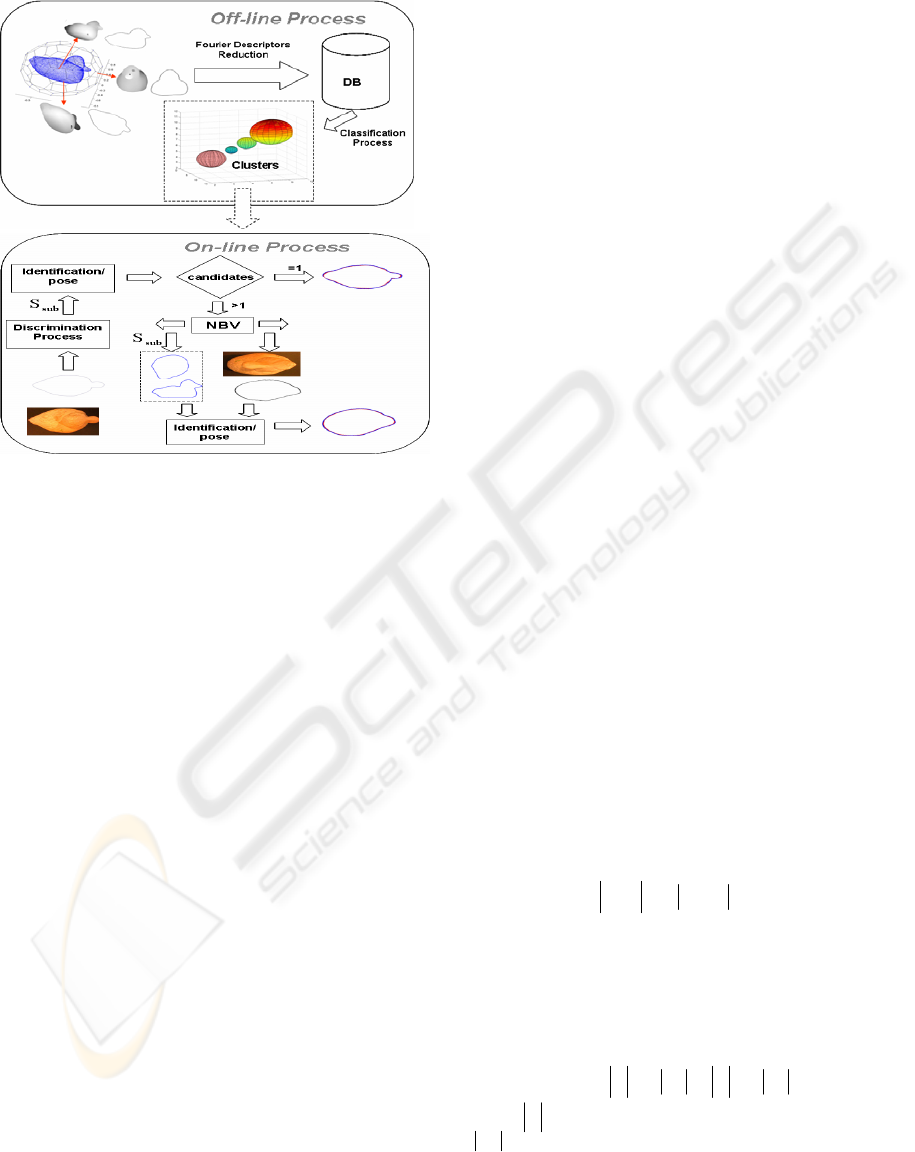
be explained in Section IV. Figure 4 shows a scheme
of the main process.
Figure 4: Diagram of the active recognition system.
3 OBJECT RECOGNITION AND
POSE ESTIMATION
PROCEDURE
Fourier descriptors can be used to represent closed
lines (silhouettes). They can be made invariant to
translations and rotations, and allow easy filtering of
image noise (
Deinzer et al., 2003). Assume a contour
l(n) composed of N points on the XY plane:
[]
1..0,)(),()( −== Nnnynxnl
(1)
where the origin of index n is an arbitrary point of
the curve, and n and n+1 are consecutive points
according to a given direction (for example
clockwise direction) over the silhouette. Assume
also that points over the curve have been regularized
in the sense that two consecutive points are always
at the same Euclidean distance. Let us define the
complex sequence and its discrete Fourier
transforms Z(k)=F(z(n))as
:
)()()( njynxnz +=
∑
−
=
−=
1
0
)/2exp()()(
N
n
NknjnzkZ
π
10 −≤≤ Nk
(2)
(3)
Assume also a data base of R silhouettes
with
),(ns
r
10 −≤≤
r
Nn R
r
≤≤1 , whose respective
discrete Fourier transforms are S
r
(k).
A critical aspect of our method is its computation
time. Then the FFT algorithm is used to obtain the
Fourier descriptors. Then N must be power of 2 and
both the scene silhouette and the silhouettes of the
data base must be regularized to a number of N = 2
speed because we want to recognize objects in real
asic problem to be solved in our method is
to
N’
points.
The b
match the scene silhouette z(n) to some silhouette
s
r*
(n) of the data base, under the assumptions that
z(n) may be scaled (
λ
), translated (
yx
jcc + ) and
rotated (
ϕ
) with respect to the ching
silhouette of the data base, and that the reference
point on z(n) (n = 0) may be different from the
reference point of that data base silhouette (we
denote that displacement
best mat
δ
). The next section deals
with selecting the silhoue es and obtaining X c,
δ
,
ϕ
,
λ
.
tt
3.1 Close Silhouettes Selection
Suppose that z is the silhouette of an object captured
r
+
by the camera and that it corresponds to the
silhouette s
r*
(n) that belongs to the silhouette
database. In general, z is matched to s
r*
(n) after
displacement, rotation, scaling and centre translation
parameters are found. In general for
),(ns
r
in the
space domain:
Dnz cjns
=
)exp()),(()(
ϕ
λ
δ
(4)
where displaces
))(( nsD
r
δ
units the in
the e u
orig of
sequenc . Taking Fo rier transform:
cNkSNkjkZ
r
+
s
)(ns
r
j
=
)()/2xp(exp)( e)(
δ
π
ϕ
λ
(5)
• Translation: Since all silhouettes have
the
coordinate origin at their centre of mass
0)0(
=
r
S and from expression (5) ,
N/Zc )0(
=
.
• Close silhouettes identification.: Defining
cNkZkZ −= )()(
, the modulus of expression
(5) holds:
)()( kSkZ
r
λ
=
(6)
The matching procedure minimizes the mean
sq
uared error between the Fourier descriptors of the
scene silhouette and the silhouettes of the database.
Given a pair of silhouettes
))(),(( nsnz
r
, the
similarity index
J is defined as
r
:
)()()(
t
ZSJ
λλ
−−=
rrr
SZ
λ
(7)
wher
e
t
NZZZ |)1(||,)0((| −=
∧∧
…
,
t
rr
r
S = NS |)1(||)0((| −…
,| . |=absolute value.
Minimizing
)(
S
λ
r
J with re
fa
spect to the scaling
ctor
λ
, we obtain:
ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS
321

r
t
r
r
t
S
r
SS
Z
=
λ
,
−= ZZJ
t
r
2
)(
r
t
r
r
t
SS
SZ
(8)
After calculating for all silhouettes of the data
ba ho
other viewpoin
3.2 Pose Calculation
the set of indexes
e silhouettes. In
r
J
se we select the sil uettes which verify UJ
r
≤
,
U being a specific threshold. In this case, we
of many ambiguous silhouettes
{
cfc2c1
S . . . ,S,S } and it is necessary to select
an t to solve the ambiguity problem
(NBV section).
have a
set
Let us denote ),,,(
21 m
rrrL …=
of the candidat order to select the
best candidate among
L
candidates, a more accurate
procedure is carried o t. This procedure uses the
complete complex Fourier descriptors (not only the
modules as in the previous process). As a result of
this process, a new similarity index
f is obtained
and the pose parameters
u
δ
ϕ
λ
,,
are ca lated.
The cost function to be ized is (see (4)):
lcu
minim
(9)
where
t
NZ −…
))(
ˆ
())(
ˆ
(),,(
δδδθλ
PqZPqZf
t
−−=
∗
,))1(
ˆ
,),0(
ˆ
(
ˆ
ZZ =
t
rrrr
NNj
NsNjssP
))/)1(2exp(
)1(,,),/2exp()1(),0(()(
−
−=
πδ
πδ
δ
…
,
∗ denotes conjugate,
∗
t
denotes transpose
co
njugate, and
r
is restricted now to set
L
Let us denote
qj =)exp(
ϕ
λ
, opt iim zing (9)
res
pect to the complex number
q :
SS
PZ
ZZf
SS
PZ
q
t
t
t
t
t
∗
∗
2
)(
δ
(10)
∗
∗
∗
−==
)(
)(,)(
δ
δδ
notice that ).
to account that
≤≤ N
(
r
t
rr
t
r
SSPP ⋅=
∗∗
)()(
δδ
Taking in
1−0 is i
δ
nteger,
th
e right expression of (10) is calculated for all
possible values of
δ
and )(
min
δ
δ
rr
ff = is
determined.
Then
r
f is the similarity index of the silhouette
r
in t fine matching process,
r
δ
is the
corresponding displacement and is obtained
from ¿the? left equation of (10) particularized to .
Rotation and scaling are estimated from :
he
r
q
r
δ
r
q
rrrr
qq ∠==
ϕλ
;
(11)
4 NEXT BEST VIEW PLANNING
The goal of this phase is to provide a solution to the
ambiguity problem by taking a set of optimal
viewpoints. When an ambiguous case occurs, we
move the camera to another viewpoint from which
the silhouettes of the candidate objects are
theoretically very dissimilar.
As said before, in our scheme representation we
associate each silhouette stored in the database with
a viewpoint of the tessellated sphere. Then, the first
step in the NBV consists of aligning the candidate
spheres (corresponding to the viewpoints in our
models) with the scene sphere.
Let T
R
(S) be the tessellated sphere, N'
Rx
the
camera position and N
R1
the viewpoint that
corresponds to the candidate silhouette . To align
the two spheres a rotation must be applied to make
N'
ci
S
Rx
and N
R1
coincident (Adán et al., 2000).
Formally:
Let
Rx
R
Rx
R
zyx
ONON
ONON
uuu
'
'
),,(
1
1
→
×
→
→
×
→
=u
be the normal
vector to the plane defined by and , O
being the center of
T
1R
ON
→
Rx
ON'
→
I
. Let
θ
be the angle between the
last two vectors. Then, a rotation
θ
around the u axis
can first be applied to
T
R
(S). This spatial
transformation is defined by the following rotation
matrix R
u
(
θ
):
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+−+−−−
−−+−+−
+−−−+−
=
θθθθθθ
θθθθθθ
θθθθθθ
θ
ccuusucuusucuu
sucuuccuusucuu
sucuusucuuccuu
zzxzyyzx
xzyyyzyx
yzxzyxxx
)1(.)1(.)1(
.)1()1(.)1(
.)1(.)1()1(
)(
u
R
(12)
where
c
θ
=cos
θ
and s
θ
=sin
θ
.
A second rotation
ϕ
around the axis
Rx
Rx
zyx
ON
ON
vvv
'
'
),,(
→
→
=v
is required to achieve
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
322

the best fitting of
T
R
(S) to T
R
(S') (see Figure 5). The
swing angle
ϕ
is determined by (14). This last set of
points can be obtained by applying a rotation matrix
Rv(
ϕ) that depends on a single parameter ϕ and can
be formally expressed as
:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+−+−−−
−−+−+−
+−−−+−
=
ϕϕϕϕϕϕ
ϕϕϕϕϕϕ
ϕϕϕϕϕϕ
ϕ
ccvvsvcvvsvcvv
svcvvccvvsvcvv
svcvvsvcvvccvv
zzxzyyzx
xzyyyzyx
yzxzyxxx
)1(.)1(.)1(
.)1()1(.)1(
.)1(.)1()1(
)(
v
R
(13)
R
1
(
ϕ
,
θ
)=R
v
(
ϕ
)·R
u
(
θ
)
(14)
Finally the alignment of the spheres is:
)(T),(R)(T
R1
'
R
SS ⋅=
θϕ
(15)
In the next step the Fourier energy is calculated
for each viewpoint.
Defining , where ,
icp
OS ∈
jcq
OS ∈
cp
S
cq
S
∈
]S...S,S[
cf2C1c
, where is the number of
candidate silhouettes, and
vp is a viewpoint from
T
f
R
(S). The energy is computed for all couples of
silhouettes as follows:
fjfiji
kZkZ
N
E
vp
Oj
N
k
vp
Oi
vp
OjOi
≤≤≠∀
−=
∑
−
=
,,
,|)()(|
1
2
1
0
,
(16)
)min(
,
vp
OjOi
vp
EE =
(17)
The NBV ν is defined as the viewpoint that
verifies:
pEE
vp
ν
ν
∀= )max(
(18)
Figure 5: Alignment process between candidate spheres
and the scene sphere.
Finally, the camera is moved to the best viewpoint
and a new image of the scene is captured and
matched with the model silhouette correspondents to
the best viewpoint using (9) and (11) equations.
Figure 6: Superimposed models after the alignment
process and energy values plotted on the nodes.
5 EXPERIMENTATION
A validation test of this method has been carried out
in our lab. The experimental setup is composed of a
Stäubli RX 90 Robot with a micro camera Jai-
CVM1000 at its end. This system controls the
position and vision direction on the camera, the
object always being centered in the scene. Figure 7
shows the experimental setup.
In the off-line process, the synthesized models
(with 80000 polygons/object) are built through a VI-
910 Konica Minolta 3D Laser scanner. At the same
time the silhouette database with their respective
Fourier descriptors are obtained and stored.
Currently we have used databases of 80 and 320
silhouettes/model.
In order to reduce redundant information and to
optimize the recognition/pose time, a Fourier
descriptors reduction has been carried out on the
silhouette models. Figure 2.a shows Fourier
descriptors modulus for an example. As X can be
seen, the first and the last descriptors are the most
meaningful. The reduction procedure consists of
considering the intervals [1,X(k)], [X(N-k),X(N)],
k=1,…N, until the error/pixel between the original
and reduced silhouettes is less than a threshold
χ
.
a) b)
Figure 7: a) Experimental Setup. b) Examples of synthetic
models.
ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS
323

The experimentation has been carried out with
19 objects that have been previously modelled with
80 and 320 views, considering descriptor reductions
of
χ
=0.05 and
χ
=0.5.
In the clustering process we have used 50
clusters. During this phase we use images with
resolution 640x480. Each silhouette in the database
was stored with a resolution of 512 points and the
database size was 12 MB (80 views) and 42 MB
(320 views).
Table 1.
# sil.
χ
t
A
ρ
A
t
B
ρ
B
0.05 2.652 1.640 2.475 2.382
80
0.5
2.047 1.653 1.863 2.473
0.05 4.901 1.089 4.739 2.107
320
0.5 3.336 1.339 3.096 2.261
The active 3D recognition system worked in all
tests achieving 100% X effectiveness. Table 1
shows the results obtained during the recognition
process without (A) and with (B) discrimination
phase. The results are compared taking into account:
the number of silhouettes of the model, threshold for
Fourier descriptors reduction (
χ
), mean square
error between the silhouette of the scene and the
estimated silhouette (
ρ). Variable t is the
computation time (seconds) on a Pentium III 800
Hhz processor.
Table II shows in detail the main process rates
using a database with 80 silhouettes/model and a
reduction factor
χ
=0.5.
From Tables 1 and 2 the following comments can
be made.
• In the whole process, most of the time is
devoted to extracting the object’s silhouette
(88,6% and 94,7%). Note that, this stage
includes several image preprocessing tasks
like filtering, thresholdin, etc. In part, such
a high percentage is also due to the fact that
we have used a reduced object database in
our experimentation. For large databases
(>100-500 objects) this percentage will
decrease at the same time that the
percentage corresponding to the candidates
selection stage will increase.
• Using 320 silhouettes per model increases
in a double the execution times with respect
the use of 80 silhouettes per model but the
ρ
decreases by 0,3 percent.
Table 2.
Algorithm
time (%)
Silhouette extraction
88.6
Identification
7.9
Pose estimation
1.4
Without
clustering
NBV
2.1
Silhouette extraction
94.7
Discrimination
0.8
Identification
2.2
Pose estimation
0.6
With
clustering
NBV
1.7
Figure 8: Comparison of discrimination between a random
method and our proposed method.
Two experiments were carried out: one running
our active recognition system which uses a random
selection of the next view, and another computing
the next best view from our D-Sphere structure. In
Figure 8 we can see the number of candidates in
each sensor position for a real case. The test average
reported that our method considerably reduced the
number of sensor movements: about 62%. The time
needed to calculate the next observation position is
very short: approximately 1.7% of all the time
needed to carry out a complete step of the
recognition process. Calculations were performed on
a Pentium III 800 Hhz processor. The active 3D
recognition system worked in all tests achieving
100% X effectiveness. Figure 9 illustrates a case of
ambiguity between two objects and how the system
solves the problem. Our NBV method shows much
higher discriminative capability than the random
method. Thus, the proposed strategy significantly
improves the recognition efficiency.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
324
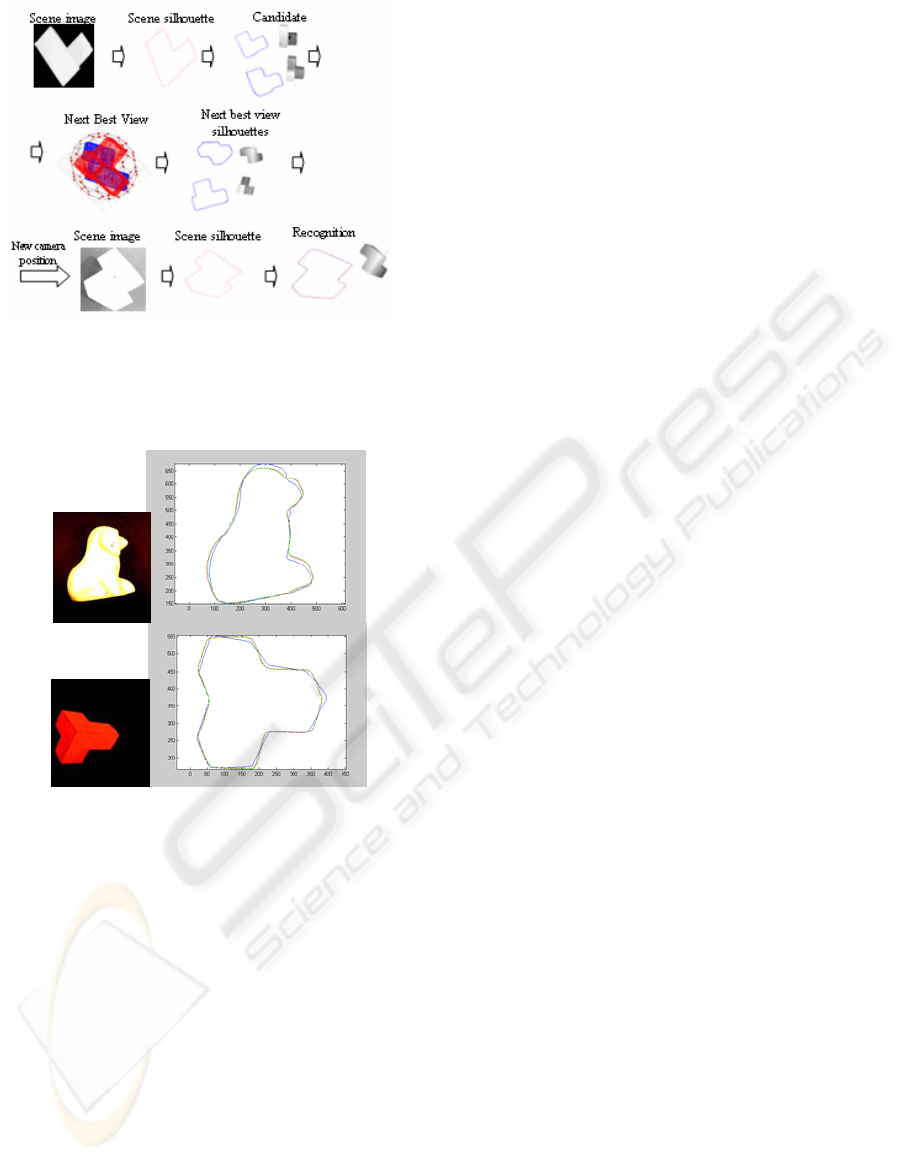
Figure 9: Solving an ambiguous case.
Figure 10 presents some matching and pose
estimation results using the proposed algorithm.
Figure 10: Some examples of 3D recognition without
ambiguity.
6 CONCLUSION
This paper has presented a new active recognition
system. The system turns a 3D object recognition
problem into a multiple silhouette recognition
problem where images of the same object from
multiple viewpoints are considered. Fourier
descriptors properties have been used to carry out
the clustering, matching and pose processes.
Our method implies the use of databases with a
very large number of stored silhouettes, but an
efficient version of the matching process with
Fourier descriptors make it possible to solve the
object recognition and pose estimation problems in a
greatly reduced computation time.
On the other hand, the next best view (NBV)
method efficiently solves the frequent ambiguity
problem in recognition systems. This method is very
robust and fast, and is able to discriminate among
very close silhouettes.
REFERENCES
Adán, A., Cerrada, C., Feliu, V., 2000. Modeling Wave
Set: Definition and Application of a New Topological
Organization For 3D Object Modeling. Computer
Vision and Image Understanding 79, pp 281-307.
Bustos, B., Kein, D.A., Saupe, D., Schreck, T., Vranic, D.,
2005. Feature-based Similarity Search in 3D Object
Databases. ACM Computing Surveys (CSUR)
37(4):345-387, Association For Computing
Machinery.
Borotschnig, H. Paletta, L., Pranti, M. and Pinz, A. H.
1999. A comparison of probabilistic, possibilistic and
evidence theoretic fusion schemes for active object
recognition. Computing, 62:293–319.
Deinzer, F., Denzler, J. and Niemann, H., 2003. Viewpoint
Selection. Planning Optimal Sequences of Views for
Object Recognition. In Computer Analysis of Images
and Patterns, pages 65-73, Groningen, Netherlands,
Springer.
Deinzer, F., Denzler, J., Derichs, C., Niemann, H., 2006:
Integrated Viewpoint Fusion and Viewpoint Selection
for Optimal Object Recognition. In: Chanteler, M.J. ;
Trucco, E. ; Fisher, R.B. (Eds.) : British Machine
Vision Conference
Helmer S. and Lowe D. G, 2004. Object Class
Recognition with Many Local Features. In Workshop
on Generative Model Based Vision 2004 (GMBV),
July.
Hutchinson S.A. and Kak. A.C., 1992. Multisensor
Strategies Using Dempster-Shafer Belief
Accumulation. In M.A. Abidi and R.C. Gonzalez,
editors, Data Fusion in Robotics and Machine
Intelligence, chapter 4, pages 165–209. Academic
Press,.
Netanyahu, N. S., Piatko, C., Silverman, R., Kanungo, T.,
Mount, D. M. and Wu, Y., 2002. An efficient k-means
clustering algorithm: Analysis and implementation.
vol 24, pages 881–892, july.
Niku S. B., 2001. Introduction to Robotics, Analysis,
Systems, Applications. Prentice Hall.
Poppe, R.W. and Poel, M., 2005. Example-based pose
estimation in monocular images using compact fourier
descriptors. CTIT Technical Report series TR-CTIT-
05-49 Centre for Telematics and Information
Technology, University of Twente, Enschede. ISSN
1381-3625
Roy, S.D., Chaudhury, S. and Banerjee. S., 2004. Active
recognition through next view planning: a survey.
Pattern Recognition 37(3):429–446, March.
Sipe M. and Casasent, D., 2002. Feature space trajectory
methods for active computer vision. IEEE Trans
PAMI, Vol. 24, pp. 1634-1643, December.
ACTIVE 3D RECOGNITION SYSTEM BASED ON FOURIER DESCRIPTORS
325
