
ADAPTIVE PREDICTIVE CONTROLLER APPLIED TO AN
OPEN WATER CANAL
Lu
´
ıs Rato, Pedro Salgueiro
CITI-UE, Universidade de
´
Evora, R. Rom
˜
ao Ramalho 59, 7000-671
´
Evora, Portugal
Jo
˜
ao Miranda Lemos
INESC-ID/IST, R. Alves Redol, 9, 1000-029 Lisboa, Portugal
Manuel Rijo
NuHCC, Universidade de
´
Evora, R. Rom
˜
ao Ramalho 59, 7000
´
Evora, Portugal
Keywords:
Water canal, SCADA system, PLC, data acquisition, adaptive control, predictive control.
Abstract:
This paper concerns to the application of adaptive control to a large scale water canal experimental plant.
Water canals are complex spatially distributed systems which aim at distributing water either for irrigating, or
domestic, or industrial purposes. In this paper a predictive adaptive control algorithm (MUSMAR) is applied to
a large scale experimental water canal prototype. The experimental facilities with a fully instrumented canal,
a PLC network and a SCADA system, are briefly described. This paper describes the developed software
module and the MUSMAR control algorithm. Finaly, Some experimental results obtained in the experimental
water canal, are presented.
1 INTRODUCTION
Water distributing systems are increasingly impor-
tant as fresh water scarcity is becoming a critical is-
sue in many places worldwide. In this increasing
water scarcity situation an efficient management of
water canals, minimising water losses, is an obvi-
ously important issue. Nevertheless, this management
task brings conflicting goals - minimise water loss
vs. Quality of Service. On one side, users demand
more and more flexibility on water withdrawing from
canals. On the other side, the use of the traditional
pre-scheduled water turns may attain a very low level
of water losses but at cost of users QoS. Thus, modern
water canals with advanced control techniques may
have and an important role on the management of
these conflicting goals.
Two strategies of upstream automatic control are
applied: local upstream control and distant upstream
control. Local control is the most practical way to
introduce automatic control on existing canals, since
every equipment can be concentrated an one place.
Nevertheless, distance upstream control as well as re-
mote supervision are promising approaches.
Adaptive control techniques are most suited to sit-
uations where the dynamic behaviour is unknown or
slowly changing. Nevertheless, the adaptive predic-
tive algorithm MUSMAR has also shown to cope well
with incomplete order modelling and minor nonlin-
earities. Thus MUSMAR has been tested and suc-
cessfully applied in several experimental processes
ranging from distributed solar power plants (Coito
et al., 1997)(Rato et al., 1997) to Internet traffic con-
trol (Costa et al., 2002).
This control approach is implemented through a
developed software package that communicates to the
supervisory control and data acquisition (SCADA)
system which is connected to a programmable logic
controller(PLC) network.
2 WATER CANAL DESCRIPTION
The experimental water canal used in this work is
at the NuHCC (N
´
ucleo de Hidr
´
aulica e Controlo de
Canais) of the University of
´
Evora, Fig. 1.
The canal has a trapezoidal cross section geom-
etry, and is constituted by four pools of roughly
40 m each, resulting in a 145 m long instrumented
canal, plus a traditional water canal which completes
a closed water circuit. The canal inlet water flow is
defined by an electrical controlled MONOVAR valve.
The flow along the four pools may be controlled by
three sluice gates and there is a water off-take up-
357
Rato L., Salgueiro P., Miranda Lemos J. and Rijo M. (2007).
ADAPTIVE PREDICTIVE CONTROLLER APPLIED TO AN OPEN WATER CANAL.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 357-360
DOI: 10.5220/0001628603570360
Copyright
c
SciTePress
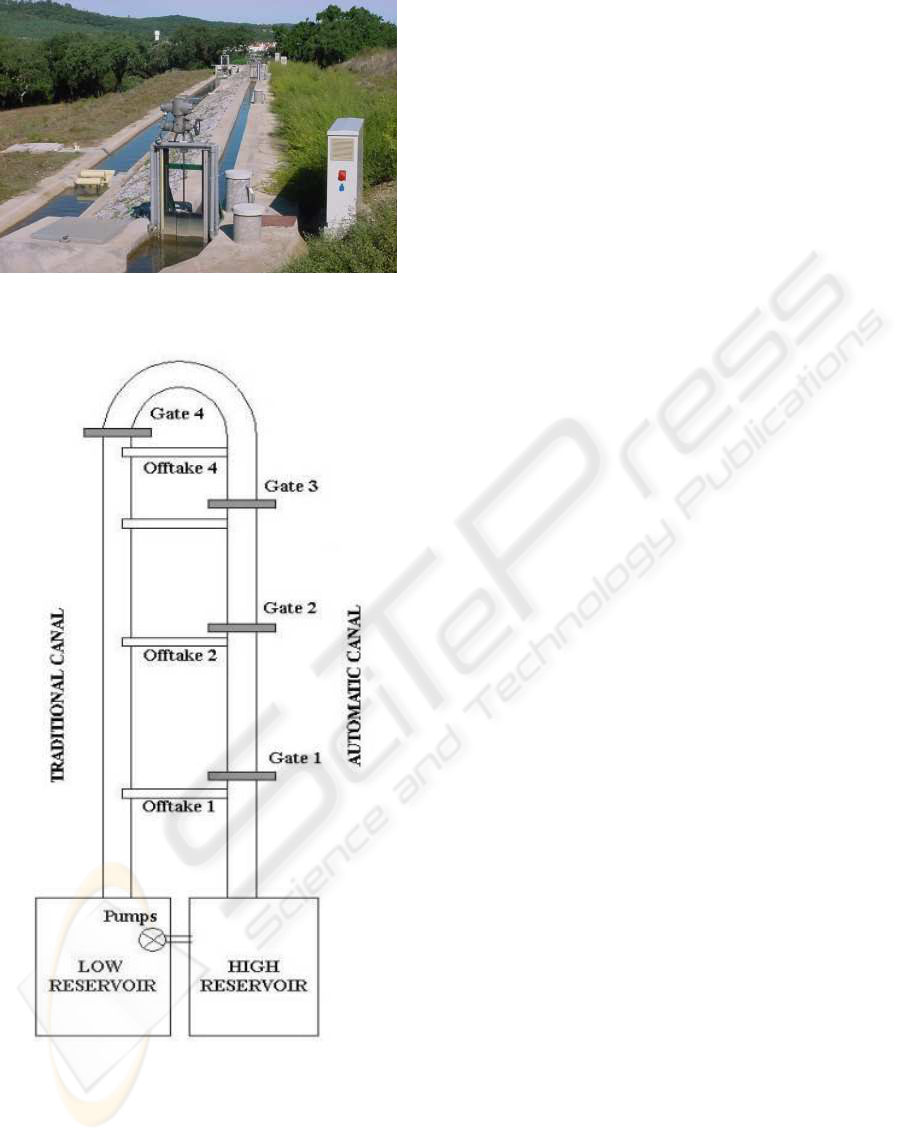
Figure 1: Experimental water canal at the University of
´
Evora.
Figure 2: Schematic diagram of the experimental water
canal at the University of
´
Evora.
stream of each gate. This off-take is equipped with
a flow meter and an electrical butterfly valve and dis-
charges into the traditional return canal. Concerning
sensors, there are three float and counter-weight level
sensors in stilling wells for each pool - one at each
end and one in the middle of the pool. Figure 2 shows
a schematic diagram of the experimental plant. This
facility is described in more detail in (Ratinho et al.,
2002).
It should be noted that the dynamic behaviour
of this type of plant is modelled by the Saint-
Venant equations which are nonlinear partial differen-
tial equations which can be linearised for small vari-
ations around stationary values. Thus, this plant be-
longs to a class of distributed parameter plants with
transport phenomena, such as highway traffic, dis-
tributed solar plants, and boiler circuits of thermal
power plants that have been studied with success in
the scope of advanced control algorithms, as adaptive
and predictive control techniques(Silva et al., 2003;
Marques and Silva, 2005).
2.1 Data Acquisition and Supervision
System
The experimental plant is equipped with a network of
6 PLCs. Five local PLCs (one for each sluice gate
or inlet valve) and one central master PLC. The data
acquisition and analog-to-digital conversion are per-
formed locally at each PLC. These are interconnected
by a MODBUS network to the master PLC, which
communicates to the SCADA computer by a serial
port RS232 interface.
The SCADA system is build over the WIZCON
environment, and presents a user friendly graphical
interface to command the process as well as to ob-
serve the evolution of measured variables over time.
The SCADA also has a DDE interface which allows
the communications between the SCADA and exter-
nal applications.
This system is described in more detail in
(Almeida et al., 2002).
2.2 Control Algorithm Software
Package
Due to the complexity of MUSMAR algorithm, it is
impracticable to implement local control directly in
the local PLCs. Moreover, although the SCADA may
implement a predefined set of controllers, it has little
support to develop general algorithms. Thus a soft-
ware package was developed in C language in order
to extend the control capabilities of the SCADA sys-
tem and implement the MUSMAR algorithm has an
external process.
Once the SCADA system has a Dynamic Data Ex-
change(DDE) communication interface, this was the
chosen process of interaction between the external
process (the controller) and the SCADA system.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
358

The initialisation, reading and writing of the vari-
ables which define the state of the process can be per-
formed through the following functions
DDEInit("WIZCON", "GATE")
DDERequest(char var[])
DDEPoke(char []var, char []valor)
These functions define the basic application program-
ming interface (API).
However, while the reading needs usually just one
call to DDERequest(), to define a command into the
actuators, several calls of DDEPoke(...) are usually
necessary, stating the control mode of one or more
(cascade) loops, and defining the variable value.
Thus, we have defined a two layer API: the base
API (dde-base.c) which communicates to the SCADA
through DDE and defines DDERequest(...) and DDE-
Poke(...); and a second layer with a more user friendly
API (scada-api.c).
This second layer defines a set of 55 functions to
read and write in or from each of the plant sensors and
actuators. The API implementation for the case of a
sluice gate is presented above.
Sluice Gates Api Implementation
We consider in the following, the case of gate API
to gate number 1, which is connected to PLC2.
The sluice gate control mode is defined by the tag
”MODE
MATIC A2”, which can take values from 1
to 4 corresponding to direct control of the actuator;
local control of sluice gate position; local control of
upstream level; and local control of downstream level.
When MODE
MATIC A2 is set to 1 it is possible
to command the gate directly with three commands:
open, close, and stop.
If the gate is closing and the desired option
is to completely open the gate it is necessary to
set MODE
MATIC A2=1 to set the direct con-
trol mode; then an order to inhibit the closing
command, MATIC CLOSE OUT A2=0, and only
then should be sent the order to open the gate
MATIC
OPEN OUT A2=1, as shown below.
void open_gate_1(){
DDEPoke("MODE_MATIC_A2", "1");
DDEPoke("MATIC_CLOSE_OUT_A2", "0");
DDEPoke("MATIC_OPEN_OUT_A2", "1");
}
Similar procedures are developed to interact with
other actuators.
Api Definition
In the API definition is listed below, ”N” stands for
the number of the PLC that controls the device.
void open_gate_N()
void close_gate_N()
float level_gate_N()
void set_level_gate_N(int level)
void close_monovar()
void open_monovar()
void set_in_flow(int flow)
void set_monovar_level(float level)
float flow_monovar_in()
float level_monovar()
float flow_valve_gN()
float level_valve_gN()
void close_valve_gN()
void open_valve_gN()
void set_valve_flow_gn(float flow)
void set_valve_level_g1(float level)
int level_upstream_canal()
int level_middle_gN()
int level_upstream_gN()
int level_downstream_gN()
Other Package Functions
Along with the API, the developed package provides
also: a simple command line; a text oriented output
interface; data logging; and a timing function. These
are functions that may be naturally adapted to the ex-
periment to be performed.
Development Environment
This package was developed in a MinGw environ-
ment. This is a set of free open-source tools for the
Windows operating system, and includes among oth-
ers: a port of the GCC compiler, a bourne shell com-
patible environment (MSYS) and a makefile utility.
3 MUSMAR ADAPTIVE
PREDICTIVE CONTROLLER
In this paper, experimental results are presented on
the application of MUSMAR, a predictive adaptive
control algorithm for which there is evidence of ro-
bustness against plant unmodelled dynamics(Mosca
et al., 1989), and have been tested in large number of
experimental plants.
At the beginning of each sampling interval, recur-
sively perform the following steps: 1. Sample the
process output at time t, compute the tracking error.
2. Using Recursive Least Squares, update the esti-
mates of the parameters in a set of predictive models.
3. Apply to the plant the control given by
u(t) = F
′
s(t) + η(t) (1)
ADAPTIVE PREDICTIVE CONTROLLER APPLIED TO AN OPEN WATER CANAL
359

Figure 3: Experimental results. Local upstream control.
Water level (mm), reference (mm), gate position (mm), time
(h).
where η is a white dither noise of small amplitude,
such that and F is the vector of controller gains, com-
puted from the estimates of the corresponding pre-
dictive models by the optimization of a cost function
across a predefined horizon T.
An integral effect has been also considered in par-
allel with MUSMAR. This algorithm has been im-
plemented in C and linked with the software package
presented above. A detailed description of MUSMAR
is presented in (Mosca et al., 1989).
4 EXPERIMENTAL RESULTS
The following results were obtained at the experimen-
tal canal with MUSMAR controller in January 2007.
In the experiment the control structure is a local
upstream one. The sampling time was set to 5 s, the
controlled variable is the level upstream of gate 2, the
manipulated variable is the position of gate 2. The
inlet flow of the canal was locally controlled to 35 l/s,
off-take valves were closed and gate 1, 3, and 4 were
opened.
Experimental results are shown in Fig.3. After the
startup the gains converge and the algorithm follows
the reference, although with a significant static error.
At instant 17,2 the integral gain was set to 0.05 elim-
inating the static error.
5 CONCLUSIONS
An adaptive predictive control algorithm and an API
software package were implemented, and tested in an
experimental process plant. The results show the ap-
plicability of advanced control algorithms in the con-
text of water canal systems. Instrumented canal plants
with centralised control and supervision are essen-
tial to the application of complex control algorithms,
which are impractical to implement on local PLCs.
As future work the inclusion of a priori information
(loading initial gains and initial covariance matrix) is
a promising step as it has been observed in other ap-
plications to be an important issue in order to apply
the MUSMAR algorithm in production environment.
ACKNOWLEDGEMENTS
This work has been supported under project FLOW -
POSC/EEA-SRI/61188/2004.
REFERENCES
Almeida, M., Figueiredo, J., and Rijo, M. (2002). Scada
configuration and control modes implementation on
an experimental water supply canal. In MED’2002,
10th Mediterranean Conference on Control and Au-
tomation, Lisbon, Portugal.
Coito, F., Lemos, J., Silva, R. N., and Mosca, E. (1997).
Adaptive control of a solar energy plant: exploit-
ing accessible disturbances. In Int. Journal of Adap-
tive Control and Signal Processing, volume 11, pages
327–342.
Costa, B., Nunes, M. S., and Lemos, J. (2002). Adaptive
predictive control of ip traffic. In MED’2002, 10th
Mediterranean Conference on Control and Automa-
tion, Lisbon, Portugal.
Marques, M. C. and Silva, R. N. (2005). Traffic simu-
lation for intelligent transportation systems develop-
ment. In IEEE Intelligent Transport Systems Confer-
ence, Viena, Austria.
Mosca, E., Zappa, G., and Lemos, J. M. (1989). Robustness
of multipredictive adaptive regulators: Musmar. In
Automatica, volume 25, pages 521–529.
Ratinho, T., Figueiredo, J., and Rijo, M. (2002). Modelling,
control and field tests on an experimental irrigation
canal. In MED’2002, 10th Mediterranean Conference
on Control and Automation, Lisbon, Portugal.
Rato, L., R. N. Silva, J. L., and Coito, F. (1997). Multirate
musmar cascade control of a distributed collector so-
lar field. In ECC’97, European Control Conference,
Brussels, Belgium.
Silva, R. N., Lemos, J., and Rato, L. (2003). Variable sam-
pling adaptive control of a distributed collector solar
field. In IEEE Trans. Control Systems Technology,
volume 11(5), pages 765–772.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
360
