SUPERVISORY CONTROL OF HEAP MODELS USING

SYNCHRONOUS COMPOSITION

Jan Komenda

Mathematical Institute, Czech Academy of Sciences, Brno Branch Zizkova 22, 616 62 Brno, Czech Republic

Jean-Louis Boimond and Sébasten Lahaye

LISA Angers, 62, Avenue Notre Dame du Lac, 49000 Angers, France

Keywords:

Heap models, synchronous product, supervisory control, dioid algebra.

Abstract:

Heaps models are powerful models for concurrent timed discrete event systems. They admit linear description

using dioid algebras. Inspired by supervisory control of logical discrete event systems we introduce parallel

composition of heap models, called synchronous product, to formally describe the action of supervisor (rep-

resented by another heap model) on the system. This additional explicit concurrency for naturally concurrent

heap models is useful for studying supervisory control in the algebraic framework of dioid algebras. Timing

aspects of supervisory control, i.e. optimal timing of the controller, is studied based on residuation theory.

1 INTRODUCTION

There are two major streams in control theory of

Discrete Event (dynamical) Systems (DES). The ﬁrst

stream, known as supervisory control theory, has

been introduced by Wonham and Ramadge for logi-

cal automata (e.g. (Ramadge and Wonham, 1989)).

The second stream more particularly deals with the

class of timed Petri nets, called timed event graphs,

based on linear representation in the (max,+) alge-

bra. Being inspired by papers on (max,+) automata

(e.g. (Gaubert and Mairesse, 1999), (Gaubert, 1995)),

which generalize both logical automata and (max,+)-

linear systems, it is interesting to develop a control

method for (max,+) automata by considering super-

visory control approach. However the time seman-

tics of the parallel composition operation (called su-

pervised product) we have proposed for control of

(max,+) automata in (Komenda et al., 2007) are dif-

ferent from the standard time semantics for timed au-

tomata or timed Petri nets. One has to increase the

number of clocks in order to deﬁne a synchronous

product of (max,+) automata viewed as 1-clock timed

automata. This goes in general beyond the class of

(max,+) automata and makes powerful algebraic re-

sults for (max,+) automata difﬁcult to use.

The results of (Gaubert and Mairesse, 1999)

suggest however an alternative for the subclass of

(max,+) automata corresponding to safe timed Petri

nets, where synchronous product is standard com-

position of subnets through shared (synchronization)

transitions. The intermediate formalism of heap mod-

els enables a letter driven (max,+)-linear representa-

tion of 1-safe timed Petri nets. Therefore it is in-

teresting to work with heaps of pieces instead of

(max,+)-automata and introduce a synchronous com-

position of heap models that yields essentially re-

duced nondeterministic (max,+)- automata represen-

tation of synchronous composition of corresponding

(max,+)-automata. This way we obtain representa-

tions allowing for use of powerful dioid algebras tech-

niques and the reduced dimension of concurrent sys-

tems at the same time: the dimension of synchronous

product of two heap models is the sum of each models

dimensions, while the dimension of supervised prod-

uct of (max,+)-automata is the product of the individ-

ual dimensions, which causes an exponential blow up

of the number of states in the number of components.

The extension of supervisory control to timed

DES represented by timed automata is mostly based

on abstraction methods (e.g. region construction turn-

ing a timed automaton into a logical one). On the

other hand abstraction methods are not suitable for

(max,+) or heap automata, because their timed se-

mantics (when weights of transitions are interpreted

as their minimal durations) are based on the earliest

467

Komenda J., Boimond J. and Lahaye S. (2007).

SUPERVISORY CONTROL OF HEAP MODELS USING SYNCHRONOUS COMPOSITION.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 467-475

DOI: 10.5220/0001636104670475

 SciTePress

possible behavior similarly as for timed Petri nets.

The method we propose avoids any abstraction and

works with timed DES (TDES) represented by heap

models. Similarly as for logical DES our approach

to supervisory control is based on the parallel compo-

sition (synchronous product) of the system with the

supervisor (another heap model).

Our research is motivated by applying supervi-

sory control on heap models, which are appropriate

to model 1-safe timed Petri nets. This is realized by

using the synchronous product: the controlled system

is the synchronous product of the system with its con-

troller (another heap model). The algebraization of

the synchronous product that is translated into idem-

potent sum of suitable block matrices together with a

linear representation of composed heap models using

its decomposed morphism matrix is then applied to

the control problem for heap models.

The paper is organized as follows. Algebraic pre-

liminaries needed in the paper are recalled in the next

section. In Section 3 are introduced heap models to-

gether with their synchronous product and their mod-

elling by ﬁxed-point equations in the dioid of for-

mal power series. Section 4 is devoted to the study

of properties of synchronous product of heap models

that will be applied in Section 5 to supervisory con-

trol of heap models. Residuation theory can be used

in supervisory control of heap models.

2 DIOID ALGEBRAS

Basic algebraic structures and their properties that

will be used in the paper are brieﬂy presented in this

section.

An idempotent semiring is a set M endowed with

two inner operations. A commutative and associative

addition denoted ⊕ that has a unit element ε and satis-

ﬁes the idempotency condition (∀a ∈ M : a⊕ a = a).

A second operation, called multiplication, and de-

noted ⊗ is associative and has a unit element e, dis-

tributes over ⊕ both on the left and on the right, and

∀a ∈ M : a ⊗ ε = ε ⊗ a = ε. An idempotent semiring

is said to be commutative if the multiplication ⊗ is

commutative.

There is a naturally deﬁned partial order  on any

idempotent semigroup, namely, a  b if and only if

a ⊕ b = b. An idempotent semiring M is called to

be complete if any nonempty subset A of M admitss

a least upper bound denoted by

x∈A

x and the dis-

tributivity axiom extends to inﬁnite sums. Idempotent

semirings are usually called dioids.

Let N denote the set of natural numbers with zero.

In complete dioids the star operation can be intro-

duced by the formula

∗

n∈N

with a

= e. Matrix dioids are introduced in the same

manner as in the conventional linear algebra.

The simplest examples of commutative dioids are

number dioids such as R

max

= (R ∪ {−∞}, max,+)

with maximum playing the role of idempotent addi-

tion, denoted by ⊕: a ⊕ b = max(a, b), and conven-

tional addition playing the role of multiplication, de-

noted by a⊗b or ab when no mistake is possible. Ex-

amples of non commutative dioids are matrix number

dioids, formal languages and formal power series.

Let us recall from (Baccelli et al., 1992) and

(Gaubert, 1992) the following results.

Theorem 2.1 Let D be a complete dioid, x,a,b in D

and

x = x⊗ a⊕ b. (1)

The least solution to equation (1) exists and is given

by b⊗ a

∗

Lemma 2.2 Let D be a complete dioid, a,b in D.

Then (a ⊕ b)

∗

= (a

∗

= a

∗

(ba

∗

)

∗

= b

∗

(ab

∗

)

∗

In the sequel we will work with the dioid of formal

power series in the noncommutative variables from A

and coefﬁcients from R

max

(corresponding to time).

The standard notation A

∗

is used for the free monoid

of ﬁnite sequences (words) from A. The empty word

is denoted by 1. Formal power series form a dioid de-

noted R

max

(A), where addition and (Cauchy or con-

volution) multiplication are deﬁned as follows. For

two formal power series in R

max

(A):

s = ⊕

w∈A

∗

s(w)w) and s

′

= ⊕

w∈A

∗

′

(w)w, we have

s⊕ s

′

= ⊕

w∈A

∗

(s(w) ⊕ s

′

(w))w and

s⊗ s

′

= ⊕

w∈A

∗

(⊕

uv=w

s(u)s

′

(v))w.

This dioid is isomorphic to the dioid of generalized

dater functions from A

∗

to R

max

via a natural isomor-

phism similarly as the dioid Z

max

(γ) of formal power

series, used to study Timed Event Graphs (TEG), is

isomorphic to the dioid of daters from Z to Z

max

This isomorphism associates to any y : A

∗

→ R

max

the formal power series ⊕

w∈A

∗

y(w)w in R

max

(A). The

zero and identity series are denoted by ε and e, re-

spectively, because it will be clear from the context

whether a number dioid or dioid of formal power se-

ries is meant. Let us recall that ∀w ∈ A

∗

: ε(w) = −∞

and

e(w) =



0 if w = 1

−∞ if w 6= 1.

We consider in the sequel the complete version of

max

(A) with coefﬁcients in R

max

∪ ∞. The notion of

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

468

projection will be needed. Similarly as for formal lan-

guages, (natural) projection will be introduced such

that it will be morphism with respect to both ⊕ and

⊗.

Finally, residuation of matrix multiplication will

be needed in Section 5. Residuation theory gener-

alizes the concept of inversion for mappings that do

not necessarily admit an inversion, in particular those

among ordered sets. If f : C → D is a mapping be-

tween two dioids, in most cases there does not exist

a solution to the equation f(x) = b. Instead of so-

lutions to this equation, the greatest solution to the

inequality f(x)  b or the least solution to the in-

equality b  f(x) are considered. In the case these

exist for all b ∈ D, the mapping f is called residu-

ated, and dually residuated, respectively. The corre-

sponding mappings that to any b ∈ D associate the

greatest, resp. least, solutions of the corresponding

inequalities are called residuated, resp. dually resid-

uated mappings. In this paper only residuated map-

pings of matrix multiplication are used. The residu-

ated mapping of the left matrix multiplication, i.e. the

greatest solution to the inequality A ⊗ X  B, is de-

noted A

◦

\B. Similarly, the residuated mapping of the

right matrix multiplication, i.e. the greatest solution

to the inequality X ⊗ A  B, is denoted B

◦

/A. Recall

from (Gaubert, 1992) that for matrices A ∈ D

m×n

,B ∈

m×p

,C ∈ D

n×p

over a complete dioid D

◦

\B ∈ D

n×p

: (A

◦

\B)

l=1

◦

l j

◦

/C ∈ D

m×n

: (B

◦

/C)

k=1

◦

We recall the notation

s∈S

s for the inﬁmal element

of a set S ⊆ D (recall that

s∈S

s is the correspond-

ing supremal element of S when lattice structure of a

complete dioid is considered).

3 SYNCHRONOUS

COMPOSITION OF HEAP

MODELS

Let us ﬁrst recall the deﬁnition of time extension

of heap models (Gaubert and Mairesse, 1999), also

called task-resource systems, which model an impor-

tant class of TDES. Formally, a heap model is the

structure

H = (A,R, r,l,u), where

• A is a ﬁnite set of pieces (also called tasks).

• R is a ﬁnite set of slots (also called resources).

• r : A → Pwr(R) gives the subset of slots required

by a piece. It is assumed that ∀a ∈ A : R(a) 6=

• l : A×R → R ∪ {−∞} is function such that l(a,r)

gives the height of the lower contour of piece a at

the slot r.

• u : A×R → R ∪{−∞} is function such that u(a,r)

gives the height of the upper contour of piece a at

the slot r. By convention, u ≥ l, l(a, r) = u(a, r) =

−∞ if r 6∈ R(a), and min

r∈R(a)

l(a, r) = 0.

The dynamics of heap models is described by row

vectors x(w)

, w ∈ A

∗

, r ∈ R corresponding to the

height of the heap w = a

... a

on slot r ∈ R. It has

been shown in (Gaubert and Mairesse, 1999) that the

upper contour of a heap w, denoted by x(w), and the

overall height of the heap w, denoted y(w), are given

by the following letter driven dynamic equations:

x(1) = (0.. .0) (2)

x(wa) = x(w)µ(a) (3)

y(w) = x(w)(0.. .0)

, (4)

where

µ(a)







0, if s = r and s 6∈ R(a)

u(a,r) − l(a,s), if r ∈ R(a) and s ∈ R(a)

−∞, otherwise

(5)

is the morphism matrix associated to the heap model

H . It is shown in (Gaubert and Mairesse, 1999) that

heap models are special (max,+)-automata with in-

put and output functions as row, resp. column vec-

tors of identity elements, and the morphism matrix

above. The (max,+)-automaton given by the triple in-

put function, output function, and the morphism ma-

trix described above is then called heap automaton.

Therefore we can associate heap models with special

(max,+)-automata called heap automata.

We assume in the deﬁnition of synchronous prod-

uct below that there are no shared resources between

two heap models. Otherwise stated: resources are

shared only by tasks within individual heap mod-

els. This requirement is best understood if one con-

siders safe timed Petri nets (which can be viewed

(Gaubert and Mairesse, 1999) as particular heap mod-

els), where synchronous compositions of subnets is

realized by synchronizing shared transitions (in heap

models tasks), while the set of places (in heap models

resources) of the individual subnets are disjoint.

Deﬁnition 3.1 (Synchronous product) Let

), i = 1, 2 be two heap models with

∩ R

0. Their synchronous product is the heap

model

= (A

∪ A

∪ R

,r,u,l) (6)

(7)

with

r(a) =







(a) ∪ r

(a), if a ∈ A

∩ A

(a), if a ∈ A

\ A

(a), if a ∈ A

\ A

SUPERVISORY CONTROL OF HEAP MODELS USING SYNCHRONOUS COMPOSITION

469

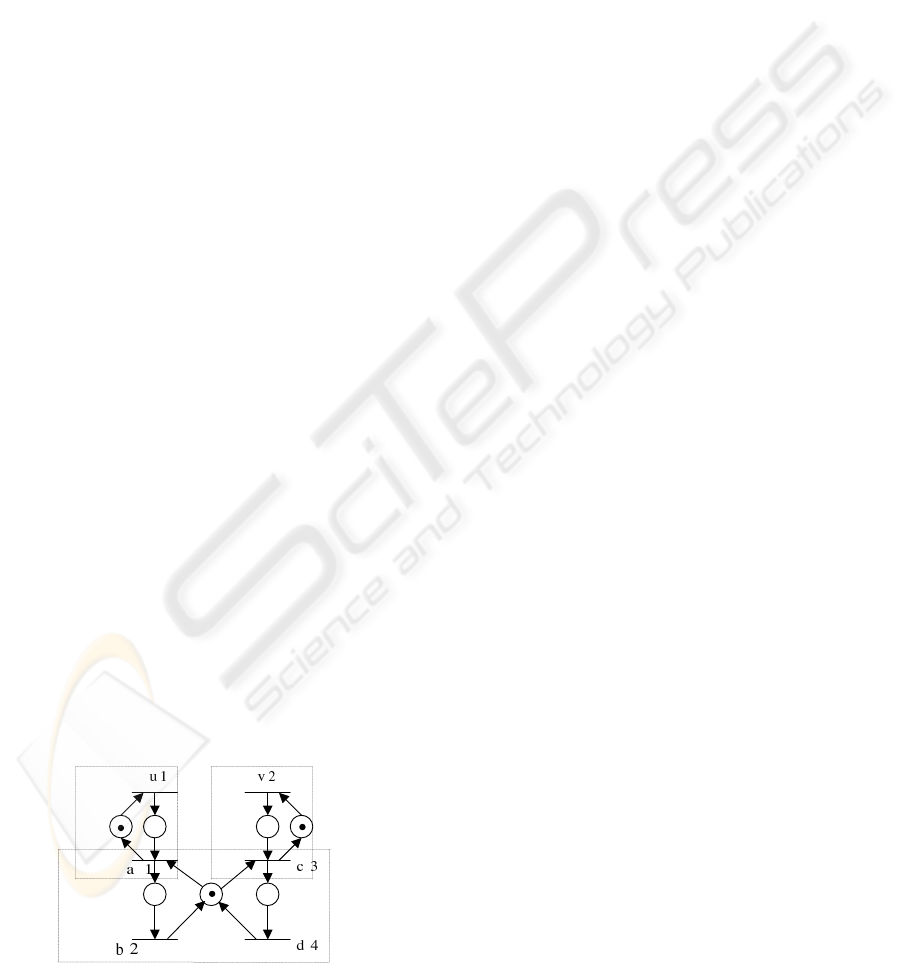
u(a,r) =



(a,r), if r ∈ R

and

l(a, r) =



(a,r), if r ∈ R

Since the slots (resources) of component heaps are

disjoint, l and u are well deﬁned: even though A

∩

0, for any r ∈ R there is only one i ∈ {1,2},

namely such that r ∈ R

, with l

(a,r) being deﬁned.

Similarly as in the supervisory control of (logi-

cal) automata the purpose of synchronous product is

twofold. Firstly, explicitly concurrent heap models

(cf. concurrent or modular automata) are heap models

built by the synchronous product of "local" heap mod-

els, whence the interest in studying the properties of

synchronous composition of heap models. Secondly,

synchronous product is used to describe the action of

the supervisor, i.e. interaction of the supervisor with

the system (cf. (Kumar and Heymann, 2000)).

Note that if the above deﬁnition is used for con-

trol purposes, it is symmetric with respect to both the

plant (say

) and the controller (say

). We then

implicitly assume in the above deﬁnition that the su-

pervisor is complete, i.e. that it never attemps to dis-

able an uncontrollable task. This is always true if all

tasks are controllable.

Now (max,+)-linear representation (2), (3), (4) of

heap models will be used in study of the morphism

matrix of the synchronous product of two heap mod-

els. An approach for just in time control of ﬂex-

ible manufacturing systems based on Petri net and

heap models, that builds upon the approach of (Men-

guy, 1997), has been developped in (Al Saba et al.,

2006). Our aim is to develop the control theory di-

rectly for heap models using synchronous composi-

tion of a heap model with its controller (another heap

model).

Let us consider the following ﬂexible manufactur-

ing system modelled by Petri net in Figure 1.

Figure 1: The Petri net model of a ﬂexible manufacturing

system.

Note that this 1-safe Petri net is T-timed (timing

is associated to transitions) and it can be decomposed

into three parts, which are synchronized using shared

(synchronization) transitions a and c. Equivalently,

each component of this Petri net can be viewed as a

separate heap model. The "global" heap model cor-

responding to the whole timed Petri net is the syn-

chronous product of "local" heap models.

An order relation on R

max

(A) will be needed for

introduction and study of control problems in Section

5. Let us recall the natural order relation on formal

power series from R

max

(A). For s,s

′

∈ R

max

(A) we

put s  s

′

iff ∀w ∈ A

∗

: s(w) ≤ s(w

′

), where in the lat-

ter inequality usual order in R

max

that coincides with

the natural order is used.

Similarly as a TEG admits a linear representation

in the dioid of formal power series Z

max

(γ) (Baccelli

et al., 1992), a heap model admits linear representa-

tion in the dioid of formal power series with noncom-

mutative variables from A: R

max

(A). As example let

us consider the following heap automaton

H .

The set of tasks is A = {a,b,c, d}. The set of re-

sources is R = {r

}. Let r(a) = r(b) = {r

}

and r(c) = r(d) = {r

}. The lower and upper con-

tours are given by

l(a, .) = [0 0 − ∞], l(b,.) = [0 0 − ∞]

l(c, .) = [0 − ∞ 0], l(d,.) = [0 − ∞ 0]

u(a,.) = [0 1 − ∞], u(b,.) = [2 0 − ∞]

u(c,.) = [0 − ∞ 3], u(d, .) = [4 − ∞ 0]

It has been shown in (Gaubert and Mairesse, 1999)

that any heap model is a special (max,+)-automaton

with the morphism matrix deﬁned in equation (5).

The graphical interpretation of the morphism matrix

is given in terms of transition weights: µ(a)

= k

means that there is a transition labelled by a ∈ A from

state i to state j with weight k provided k 6= −∞,

in case k = −∞ there is no transition from i to j.

Note that the morphism matrix µ of a heap model

can be also considered as element of R

max

(A)

|R|×|R|

i.e. µ = ⊕

w∈A

∗

µ(w)w by extending the deﬁnition of µ

from a ∈ A to w ∈ A

∗

using the morphism property

µ(a

... a

) = µ(a

).. .µ(a

However µ has an important property of being ﬁnitely

generated, because it is completely determined by its

values on A. For this reason we have in fact µ

∗

(⊕

a∈A

µ(a)a)

∗

. Since we are interested in behaviors

of heap models that are given in terms of µ

∗

we abuse

the notation and write simply µ = ⊕

a∈A

µ(a)a.

The corresponding heap automaton is in Figure

2 below. The state vector is associated to resources

H variables (formal power series) x

∈

max

(A) from left to right. We obtain the following

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

470

Figure 2: Example of a heap automaton.

equations in dioid R

max

(A) endowed with pointwise

addition and convolution multiplication:

= x

⊗ (0a⊕ 2b⊕ 0c⊕ 4d) ⊕ x

⊗ (0a⊕ 2b)

⊕ x

⊗ (0c⊕ 4d) ⊕ e

= x

⊗ (1a⊕ 0b)⊕ x

⊗ (1a⊕ 0b⊕ 0c⊕ 0d) ⊕ e

= x

⊗ (3c⊕ 0d) ⊕ x

⊗ (0a⊕ 0b⊕ 3c⊕ 0d) ⊕ e

y = x

⊕ x

The corresponding matrix form is

x = xµ⊕ α

y = xβ,

with x = (x

), α = (e e e), β = (e e e)

, µ =





0a⊕ 2b⊕0c⊕ 4d 1a⊕ 0b 3c⊕ 0d

0a⊕ 2b 1a⊕ 0b⊕ 0c⊕ 0d ε

0c⊕ 4d ε 0a⊕ 0b⊕3c⊕ 0d





In general we have the following linear description

of (max,+) automata in the dioid R

max

(A) of formal

power series:

x = xµ⊕ α (8)

y = xβ, (9)

where µ =

a∈A

µ(a)a ∈ R

max

(A) is also called the

morphism matrix.

Recall that the least solution to this equation is y=

αµ

∗

β.

4 MORPHISM MATRIX OF

SYNCHRONOUS PRODUCT OF

HEAP MODELS

Since we introduce supervisory control of heap mod-

els using the synchronous product of the plant heap

model with the controller heap model, it is impor-

tant to study properties of the synchronous product.

In this section the behavior of a synchronous prod-

uct of two heap models will be represented in terms

of morphism matrix of the synchronous product. Ac-

cording to Deﬁnition 3.1, the dimension (here number

of resources) of the synchronous product of subsys-

tems is the sum of dimensions of each subsystem. It

should be intuitively clear that morphism matrices of

synchronous products are block matrices, where the

blocks are formed according to dimensions (number

of resources) of the component heap models.

In order to simplify the approach we require that

l(a, r) = 0 whenever r ∈ R(a), which simply means

that pieces are on the ground in all slots. Thus, the

upper contour gives information about the duration of

tasks for different resources used. We recall at this

point that l(a, r) = −∞ for r 6∈ R(a).

Let

and

be two heap models with mor-

phism matrices denoted by µ

and µ

, respectively.

Let ε

, i, j = 1,2 be the rectangular matrices of ze-

ros (−∞) of dimensions m

× m

and E

, i = 1,2 the

square (max,+)-identity matrices of dimensions m

. We have the following block form of µ

(a), a ∈

Theorem 4.1 The morphism matrix of

H = H

admits the following decomposition:

• If a ∈ A

∩ A

then:

(a) =



(a)

(a) µ

(a)



, where

(a)



(a)

′

: i

′

∈ r

(a) arb., if i ∈ r

(a)

−∞, if i 6∈ r

(a)

and

(a)



(a)

′

: i

′

∈ r

(a) arb., if i ∈ r

(a)

−∞, if i 6∈ r

(a)

• If a ∈ A

\ A

then :

(a) =



(a) ε



• If a ∈ A

\ A

then:

(a) =



(a)



Proof For a ∈ A = A

∪ A

three cases must be dis-

tinguished. Firstly, a ∈ A

∩ A

is a shared task. Then

for resources r,s from R

∪ R

there are four possi-

bilities depending on whether these are in R

or R

whence the block form of µ

(a). We recall here

that R

∩ R

0. It is easy to see that in the diago-

nal blocks the individual morphism matrices appear.

Also,

(a)











u(a, j) − l(a,i) = u

(a, j)

if i ∈ R

(a) and j ∈ R

(a)

−∞

if i 6∈ R

(a) or j 6∈ R

(a)

SUPERVISORY CONTROL OF HEAP MODELS USING SYNCHRONOUS COMPOSITION

471

and similarly for µ

(a). Since µ

(a)

equals either

(a, j)(for i ∈ r

(a) and j ∈ r

(a)) or −∞ otherwise,

we can see that the rows corresponding to i ∈ r

(a)

(a), i.e. µ

(a)(i,.), are the same as the rows

(a)(i

′

,.) for i

′

∈ r

(a), which are all the same, i.e.

an arbitrary one can be taken. Thus, the correspond-

ing entry does not depend on j anymore. Hence, the

morphism matrix of the composed heap µ

(a) has

the claimed form. In the much easier situation when

a ∈ A

\ A

it is sufﬁcient to notice that no resource

from R

is used by a. It is easily seen that µ

(a) has

again the claimed form. Finally, the case a ∈ A

\ A

is symmetric.

Theorem 4.1 can be generalized to n ∈ N, where

morphism matrix of synchronous product are matri-

ces with n× n blocks. This is useful for decentralized

control, but in this paper we only need synchronous

product of the system with its controller.

We recall at this point that

a∈A

(a) ⊗ a ∈ R

max

(A).

The algebraization of synchronous product pre-

sented in this section will be useful for control pur-

poses in the next section.

5 SUPERVISORY CONTROL OF

HEAP MODELS

In this section supervisory control of heap models is

studied. The aim is to satisfy a behavioral speciﬁca-

tion given by a formal power series. The closed-loop

system is represented by parallel composition (syn-

chronous product) of the plant with a supervisor to be

found, which is itself represented by a heap model.

In general a supervisor acts on both timing and

logical properties of the plant’s behavior under su-

pervision. Since heap models are special (max,+)-

automata there are two aspects of supervision: dis-

abling and delaying of tasks (events). Here we are

only interested in delaying the different tasks which

is similar to control of TEG in the maxplus algebra,

where input transitions are added in order to delay the

timed behavior of a TEG.

Now we show how Theorem 4.1 can be used

for control of heap models. The synchronous prod-

uct of heap models G = (A

) and C =

) of dimensions m and n corresponds

to the controlled (closed-loop) system. The event al-

phabet of the controlled system is denoted by A. Ac-

cording to Deﬁnition 3.1, we have A = A

∪A

. Let us

denote the morphism matrices of G and C by µ

and

, respectively. Now let us return to the description

of behaviors of heap models in the dioid of formal

power series R

max

(A). The vector of formal power

series from R

max

(A) associated to generalized dater

functions x

G kC

: A

∗

→ R

m×n

max

satisﬁes the following

equations:

G kC

= x

G kC

⊕ α, (10)

G kC

= x

G kC

β, (11)

where µ

G kC

is the morphism matrix of

G kC , α and

β are row, resp. column, vectors of 0’s of dimen-

sion m + n. The structure of the morphism matrix

described in Theorem 4.1 is now used for control pur-

poses. According to Theorem 2.1 the greatest solu-

tions to equations (10) and (11) are

G kC

= αµ

∗

G kC

, (12)

G kC

= αµ

∗

G kC

β, (13)

whence an interest in studying properties of µ

∗

G kC

Given a speciﬁcation behavior (e.g. language or

formal power series), the goal in supervisory control

of DES is to ﬁnd a supervisor that achieves this speci-

ﬁcation as the behavior of the controlled system. In

a ﬁrst approach we assume, similarly as in control

of TEG, that the structure of the controller is given,

which means here that the controller heap model only

delays task executions of the plant. This is done by

the choice of upper contour functions ( i.e. duration of

controller’s tasks) from µ

(u). The delaying effect of

the controller is naturally realized via its tasks (tran-

sitions of the corresponding heap automaton) shared

with the plant heap.

The morphism matrix of the composed system is

given by

C kG

u∈A

C kG

(u)u⊕

a∈A

∩A

C kG

(a)a

⊕

a∈A

C kG

(a)a.

In order to simplify the approach our attention is

from now on limited to the case A

= A

, which is a

standard assumption in the supervisory control with

complete observations. Since state vector in equa-

tion (8) is associated to resources, it can be written as

C kG

= (x u), where the ﬁrst component corresponds

to the (uncontrolled) plant heap and the second to the

controller heap. Owing to Theorem 4.1 we have:

(x u) = (x u)

a∈A



H(a)a

F(a)a

H(a)a F(a)a



⊕ (α

,α

where α

and α

are vectors of zeros of correspond-

ing dimensions, µ

(a) is for convenience denoted by

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

472

H(a), µ

(a) by

H(a), µ

(a) by F(a), and µ

(a) by

F(a). This can be written as

(x u) = (x u)



A F



⊕ α,

where H =

a∈A

H(a)a and similarly for F,

F, and

H. Hence,

x = xH ⊕ u

H ⊕ α

u = x

F ⊕ uF ⊕ α

Theorem 2.1 yields u = (x

F ⊕ α

∗

as the least

solution of the second equation, which substituted

into the ﬁrst equation leads to

x = xH ⊕



F ⊕ α

∗



H ⊕ α

The least solution is given by

x = (α

∗

H ⊕ α

)(H ⊕

∗

. (14)

The last equation can be viewed as the expression

of the closed-loop system using the feedback given

by F. Notice that unlike classical control theory the

control variables have their inner dynamics, which is

caused by adopting a supervisory control approach,

where a controller is itself a dynamical system of the

same kind as the uncontrolled system. Therefore, our

F, which plays the role of feedback mapping, is de-

termined by inner dynamics of the controller given by

its morphism matrix F.

There is a strong analogy with the feedback ap-

proach for control of TEG, see (Cottenceau et al.,

2001), which should not be surprising, because super-

visory control (realized here by synchronous product)

is based on a feedback control architecture. In super-

visory control the control speciﬁcation (as counterpart

of reference output from control of TEG using dioid

algebras) are given in terms of behaviors of (max,+)

automata (i.e. formal power series). In fact, for a ref-

erence output y

ref

we are interested in the greatest F

such that

y ≤ y

ref

thus,

(α

∗

H ⊕ α

)(H ⊕

∗

β ≤ y

ref

. (15)

We obtain from Lemma 2.2 that

(H ⊕

∗

= H

∗

(

∗

)

∗

,i.e.

inequality (15) becomes

(α

∗

H ⊕ α

∗

(

∗

)

∗

β ≤ y

ref

(16)

Note that while ⊗ and ⊕ are lower semicontinu-

ous and residuated, the Kleene star is not in general,

but only when the image is suitably constrained (in

which case it is trivially residuated with identity as

the corresponding residuated mapping). Moreover,

as follows from Theorem 4.1,

F can be simply ex-

pressed using F. Hence, there is a hope that at least

in some special cases residuation theory (see Section

2) can be applied to obtain the greatest series F cor-

responding to the "controller part" of the morphism

matrix µ

G kC

such that y

G kC

satisﬁes a given speciﬁ-

cation (e.g. is less than or equal to a given reference

output series y

ref

). In fact we obtain from the above

inequality the greatest

∗

such that inequality (16)

is satisﬁed. Thus it is not an easy problem. The sit-

uation is much simpler in case

F = F and

H = H.

This is satisﬁed if we assume that the controller heap

model has the same number of resources as the un-

controlled heap model and the logical structure of the

controller (given by r

: A → Pwr(R

)) mimicks the

structure of the plant, formally there exists an isomor-

phism between R

and R

such that r

and r

are equal

up to this isomorphism. In terms of Petri nets this

can be interpreted as having a controller net with the

same net topology (i.e. logical structure as the uncon-

trolled net), i.e. in the closed-loop system there are

always parallel places of the controller corresponding

to places of the uncontrolled net. The role of the con-

troller is only to act on the system through holding

times of the controller’s places that correct the hold-

ing times of the places in the original net. Because of

the ﬁxed parallel structure of the controller it is clear

that the controller can in this case only delay the ﬁring

of the transitions, which are all shared by the system

and the controller.

It is easy to check that Theorem 4.1 in such a case

gives

F = F as well as

H = H and α

= α

= α, row

vector of zeros of dimension n. Hence, inequality (15)

becomes α(F

∗

H ⊕ E)(H ⊕

∗

β ≤ y

ref

, where

E is the identity matrix. An easy calculation yields

(H ⊕

∗

H) = (E ⊕ F

)H = F

∗

H, hence

∗

H ⊕ E)(F

∗

= (F

∗

⊕ (F

∗

= (F

∗

Thus, y = α(F

∗

β ≤ y

ref

, i.e. the problem is to ﬁnd

the greatest F such that

∗

≤ α

◦

ref

◦

/β.

Since the Kleene star is not a residuated mapping

in general, such a problem has only a solution if

◦

ref

◦

/β, playing the role of reference model G

ref

from (Cottenceau et al., 2001) is of a special form to

be studied. Let us notice that H ≥ E, which follows

from the form of morphism matrix and the usual as-

sumption that any resource of the system is used by

at least one task: ∀r ∈ R

∃a ∈ A such that r ∈ r

(A).

The following Lemma is useful.

Lemma 5.1 If H ≥ E then for any B ∈ R

max

(A)

n×n

every solution of (X

∗

≤ B is a solution of

H(X

∗

≤ B and vice versa.

SUPERVISORY CONTROL OF HEAP MODELS USING SYNCHRONOUS COMPOSITION

473

Proof If X a solution of (X

∗

≤ B, then (X

∗

E ⊕(X

∗

≤ B, hence also (X

∗

≤ B. Therefore,

H(X

∗

≤ X

∗

H(X

∗

= (X

∗

≤ B,

where the ﬁrst inequality follows from isotony of mul-

tiplication and E ≤ X

∗

. Conversely, if X is a solu-

tion of H(X

∗

≤ B, then (X

∗

= E ⊗ (X

∗

≤

H(X

∗

≤ B as follows from isotony of multiplica-

tion and the assumption that E ≤ H.

Using Lemma 5.1 our problem is to ﬁnd the greatest

solution in F of

H(F

∗

≤ α

◦

ref

◦

/β.

It follows from Lemma 2.2 that

H(F

∗

= (H ⊕ F)

∗

= H

∗

(FH

∗

)

∗

thus we get formally the same problem as the one

solved in (Cottenceau et al., 2001) with H

∗

playing

the role of transfer function H in the TEG setting.

The following result adapted from (Cottenceau et al.,

2001), Proposition 3, is useful: If there exists D ∈

max

(A) such that α

◦

ref

◦

/β = H

∗

or there exists

′

∈ R

max

(A) such that α

◦

ref

◦

/β = D

′∗

∗

then there

exists the greatest F such that H

∗

(FH

∗

)

∗

≤ α

◦

ref

◦

/β,

namely

opt

= H

∗

◦

\[α

◦

ref

◦

/β]

◦

∗

= αH

∗

◦

ref

◦

∗

β.

In the special case we have restricted attention to, our

methods yields the gretest feedback such that timing

speciﬁcation given by y

ref

is satisﬁed, provided y

ref

is of one of the special forms. In the special case of a

controller with ﬁxed logical structure only timed be-

havior is under control.

If we are interested in manufacturing systems,

where speciﬁcatons are given in terms of Petri nets,

the reference output is not typically required to be met

for all sequences of tasks, but only those having a real

interpretation. These are given by the correponding

(logical) Petri net language, say L. Thus, the problem

is to ﬁnd the greatest F, such that

αH

∗

(FH

∗

)

∗

β char(L) ≤ y

ref

char(L),

where char(L) =

w∈L

e.w is the series with Boolean

coefﬁcients, i.e. the formal series of language L. Let

us recall (Gaubert and Mairesse, 1999) that such a

restricton is formally realized by the tensor product

(residuable operation) of the heap automaton with the

logical (marking) automaton recognizing the Petri net

language L, which is compatible with Theorem 4.1 of

(Komenda et al., 2007).

Note that speciﬁcations based on (multivariable)

formal power series are not easy to obtain in many

practical problems, in particular those coming from

production systems, often represented by Petri nets.

In fact, given a reference output series amounts to

solve a scheduling problem. A formal power series

speciﬁcation is not given, but it is to be found: e.g.

using Jackson rule (Jackson, 1955).

6 CONCLUSION

It has been shown how methods of dioid algebras can

be used in supervisory control of heap models. We

have proposed a synchronous product of heap models.

The structure of the morphism matrix of synchronous

product of two heap models is derived and applied to

control of heap models.

The present reseach is a very ﬁrst step in control

of heap automata. Sharing of resources is only al-

lowed inside component heap models. Of potential

interest is supervisory control with partial controlla-

bility, partial observations, and decentralized control

of heap automata.

ACKNOWLEDGEMENTS

Partial ﬁnancial support of Université d’Angers, of

the Grant Agency GA AV No. KJB100190609, and

of the Academy of Sciences of the Czech Republic,

Institutional Research Plan No. AV0Z10190503 is

gratefully acknowledged.

REFERENCES

M. Al Saba, J.L. Boimond, and S. Lahaye. On just in time

control of ﬂexible manufacturing systems via dioid

algebra. Proceedings of INCOM’06, Saint-Etienne,

France, vol.2, pp. 137-142, 2006.

F. Baccelli, G. Cohen, G.J. Olsder and J.P.Quadrat (1992).

Synchronization and linearity. An algebra for discrete

event systems. New York, Wiley.

B. Cottenceau, L. Hardouin, J.L. Boimond, and J.L. Ferrier.

Model Reference Control for Timed Event Graphs in

Dioid, Automatica, vol. 37, pp. 1451-1458, 2001.

S. Gaubert. Théorie des systèmes linéaires dans les dioïdes.

Thèse de doctorat, Ecole des Mines de Paris, 1992.

S. Gaubert. Performance evaluation of (max,+) automata,

IEEE Trans. on Automatic Control, 40(12), pp. 2014-

2025, 1995.

S. Gaubert and J. Mairesse. Task resource models and

(max,+) automata, In J. Gunawardena, Editor: Idem-

potency. Cambridge University Press, 1997.

S. Gaubert and J. Mairesse. Modeling and analysis of timed

Petri nets using heaps of pieces. IEEE Trans. on Au-

tomatic Control, 44(4): 683-698, 1999.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

474

J.R. Jackson. Scheduling a Production Line to Minimize

Maximum Tardiness. Research report 43. University

of California Los Angeles. Management Science Re-

search Project.

J.Komenda, M.Al Saba, and J.L. Boimond. Supervisory

Control of Maxplus Automata: Quantitative Aspects.

In Proceedings ECC 2007, Kos (Greece).

R. Kumar, M. Heymann. Masked prioritized synchroniza-

tion for interaction and control of discrete-event sys-

tems, IEEE Transaction Automatic Control 45, 1970-

1982, 2000.

F. Lin and W.M. Wonham, On Observability of Discrete-

Event Systems, Information Sciences, 44: 173-198, 1

E. Menguy. Contribution à la commande des systèmes

linaires dans les diodes. Thèse de doctorat, Université

d’Angers, 1997.

P.J. Ramadge and W.M. Wonham. The Control of Discrete-

Event Systems. Proc. IEEE, 77:81-98, 1989.

J. Sifakis and S. Yovine. Compositional speciﬁcation of

timed systems. Proceedings of the 13th Symp. on The-

oretical Aspects of Computer Science, STACS’96, pp.

347-359, 1996. LNCS 1046.

SUPERVISORY CONTROL OF HEAP MODELS USING SYNCHRONOUS COMPOSITION

475