HIERARCHICAL SPLINE PATH PLANNING METHOD FOR

COMPLEX ENVIRONMENTS

Martin Saska, Martin Hess and Klaus Schilling

University of Wuerzburg, Germany

Informatics VII, Robotics and Telematics

Am Hubland, Wuerzburg, Germany, 97074

Keywords:

Path planning, Mobile robots, PSO, Spline path, Hierarchical approach.

Abstract:

Path planning and obstacle avoidance algorithms are requested for robots working in more and more compli-

cated environments. Standard methods usually reduce these tasks to the search of a path composed from lines

and circles or the planning is executed only with respect to a local neighborhood of the robot. Sophisticated

techniques allow to ﬁnd more natural trajectories for mobile robots, but applications are often limited to the

ofﬂine case.

The novel hierarchical method presented in this paper is able to ﬁnd a long path in a huge environment with

several thousand obstacles in real time. The solution, consisting of multiple cubic splines, is optimized by

Particle Swarm Optimization with respect to execution time and safeness. The generated spline paths result in

smooth trajectories which can be followed effectively by nonholonomic robots.

The developed algorithm was intensively tested in various simulations and statistical results were used to

determine crucial parameters. Qualities of the method were veriﬁed by comparing the method with a simple

PSO path planning approach.

1 INTRODUCTION

Expanding mobile robotics to complicated envi-

ronments increases the requirements on the con-

trol system of the robot. The desired task has

to be executed by the robot as fast as possible in

these scenarios. Standard path planning approaches

very often just provide simple piecewise constant

routes (Latombe, 1996),(Kunigahalli and Russell,

1994),(Franklin et al., 1985) or only local optimal so-

lutions (Borenstein and Koren, 1991),(Khatib, 1986).

Few methods that give continues and smooth solu-

tion (Azariadis and Aspragathos, 2005), (Nearchou,

1998), due to long computational time in order of

minutes, cannot be used in real time applications.

All path planning methods try to ﬁnd a path from an

actual position S of the controlled robot to a desired

goal position G, with regard to position and shape of

known obstacles O. While these parameters stand as

the inputs of the algorithm, the output can be either an

optimal path from S to G or just a direction from the

actual position respecting locally optimal trajectory.

The key issue of the path planning for mobile robots

is how to deﬁne the best trajectory. A common an-

swer to this is that the optimal path should be similar

to a path designed by a human operator. This vague

deﬁnition can be expressed by a penalty function that

is minimized during the planning. The simplest ver-

sion of the function consists of two parts. While the

ﬁrst one evaluates a length of the path (or time needed

to goal fulﬁlment), the second part ensures safety of

the path (i.e. sufﬁcient distance to obstacles). So ﬁnd-

ing an acceptable compromise between these require-

ments is the core problem of the path planning itself.

The novel approach presented in this paper offers

a solution to the above mentioned problems. The

output of the algorithm is a path, which consists of

smoothly connected cubic splines. Spline paths are

naturally executable by the robot and optimization

of the speed proﬁle can be easily done by modiﬁca-

tions of the radius of the curvature. Global informa-

tion about the workspace is subsumed, because the

whole space of spline trajectories from S to G will

be searched through during the optimization process.

Therefore big clusters of obstacles as well as huge

obstacles in the environment can be avoided imme-

diately. This enables us to locate the ﬁnal solution in

the areas with lower density of obstacles at the begin-

ning of the mission. Such a path may seem longer,

due to necessary deviations from the ”bee-line”, but

116

Saska M., Hess M. and Schilling K. (2007).

HIERARCHICAL SPLINE PATH PLANNING METHOD FOR COMPLEX ENVIRONMENTS.

In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 116-123

DOI: 10.5220/0001640001160123

 SciTePress

the ﬁnal movement time can be shorter, because difﬁ-

cult maneuvers in the obstacle clusters are eliminated.

Particle Swarm Optimization (PSO) (Eberhart and

Kennedy, 1995) was used for prospecting the optimal

solution hereunder due to its relatively fast conver-

gence, its global search character and its ability to

avoid local minima. In this paper is supposed real

time path planning and therefore the solution must

be given in a split second. The complexity of PSO

strongly depends on the dimension of the search space

and on the needed swarm size. The number of iter-

ations increase more than exponentially with the di-

mension. Accordingly a minimal length of the parti-

cle is required, but in complex environments a short

string of cubic splines is not sufﬁcient and collision

free path in such limited space often does not exist.

In the proposed algorithm, that is based on a hi-

erarchical approach, the PSO process is used several

times. Each optimization proceeds in a subspace with

a small dimension, but the total size of the ﬁnal so-

lution can be unlimited. The path obtained by this

method is only suboptimal, but the reduction of the

computational time is incomparable bigger. In addi-

tion the algorithm can be started without prior knowl-

edge about the complexity of the environment, be-

cause the dimension of the search space is speciﬁed

during the planning process. The dimension even may

not be uniform in the whole workspace, but it is au-

tomatically adapted according to the number of col-

lisions along the path, that is found by the hierarchi-

cally plunging.

The paper is organized as followed: A novel

method reﬂecting special requirements for the mobile

robots in a complex environment is presented in sec-

tion 2. Section 2.1 provides information about the

universal PSO approach. In section 2.2 adaptations

of the PSO to our speciﬁc problem are described. Af-

ter this experimental results are presented in section

3 followed by concluding words and plans for future

work in section 4.

2 PATH PLANNING

The path planning approach presented in this pa-

per is based on a searching through a space of

states P . Each state P

is represented by a vector

= (P

i,x

, P

i,y

, P

′

i,x

, P

′

i,y

), that denotes position and

heading of the robot in the workspace. The ﬁnal path

of the robot is set by a transition P

→ P

i+1

between

each pair of neighboring states. T

can be deﬁned

uniquely, if T ≡ C

, where C

is the set of cubic

splines with smooth ﬁrst derivation (closely described

in 2.2).

The system of all solutions Π is a vector

Π = < S, G, p, t, f(t) >, where S, G ∈ P are start

and goal states of the robot and p ⊂ P is a sequence

of the states between S and G. t ⊂ T is a string of

the splines connecting S and G and f(t) is the ﬁtness

function denoting the quality of the found path. The

solution π ∈ Π with minimum value of f (t) should

conform with the best path.

The crucial problem is to ﬁnd π with minimum or

nearly minimum value of the ﬁtness function in the

usually vast set Π. The complexity of the task grows

with the size of vector p. Solutions with a small

dimension of p can be found faster, but a collision

free path may not exist in such limited space, if the

workspace of the robot is too complicated.

Higher-level

planning

PSOmodule

Collision

detection

Control

module

MAP

Path

planning

Start,Goal

Control

points

Start

Goal

Controlpoints

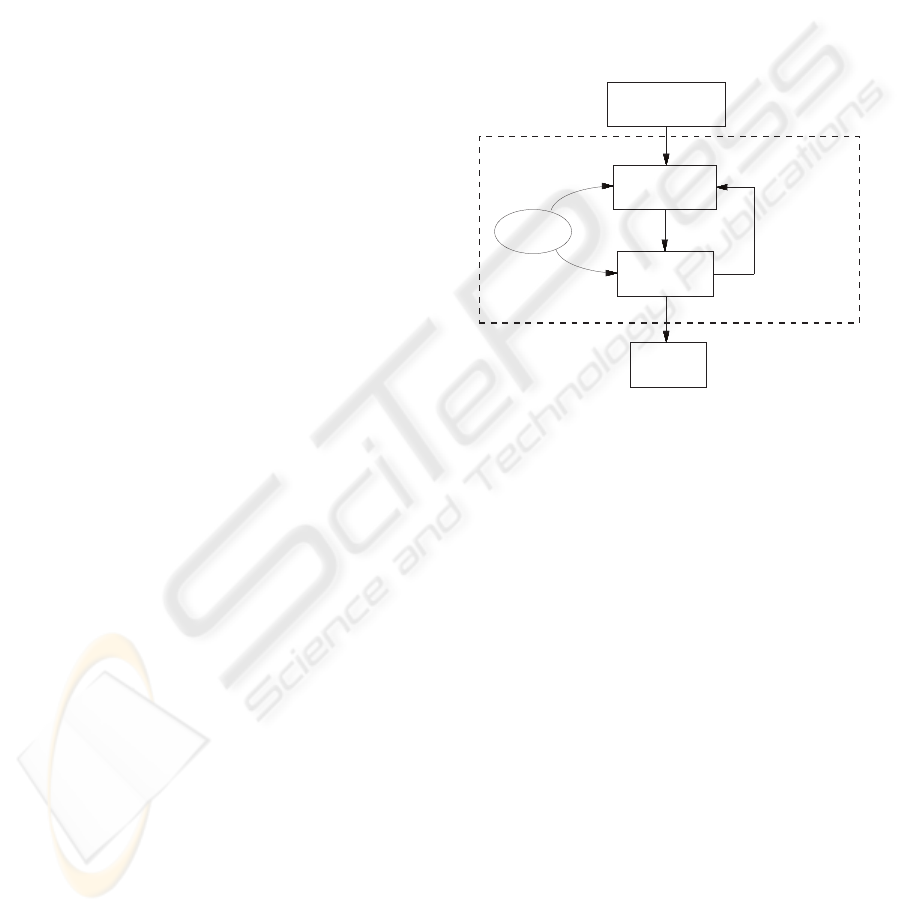
Figure 1: Schema of the presented hierarchical method.

In the hierarchical approach presented in this pa-

per the optimization task is decomposed to multiple

subtasks. The basic idea of the algorithm can be seen

in Fig. 1. The actual state of the robot and the de-

sired state generated by a higher planning module are

the inputs for the Particle Swarm Optimization (de-

scribed in 2.1). The path t which was found by PSO

is checked in the collision detection module and a

collision free solution is sent to the control module,

where the path is executed. If a collision is detected,

the string of splines t is divided and control points of

each spline are used as new input for the PSO module.

These points are put into the memory of the module

sequently. For other optimization processes always

the last added points are chosen. This ”LIFO” ap-

proach guarantees that the path close to the robot will

be found as soon as possible. The remaining path will

be found during the robot’s movement. Therefore the

time needed for the initial planning before the start of

the mission is reduced several times.

An example of the path decomposition is shown in

Fig. 2. Each vector p used in the optimization pro-

cesses contains only two states P

which correspond

to three splines in the string. In this simpliﬁed exam-

ple the hierarchical process is stopped always in the

third level, independently of the number of collisions.

HIERARCHICAL SPLINE PATH PLANNING METHOD FOR COMPLEX ENVIRONMENTS

117

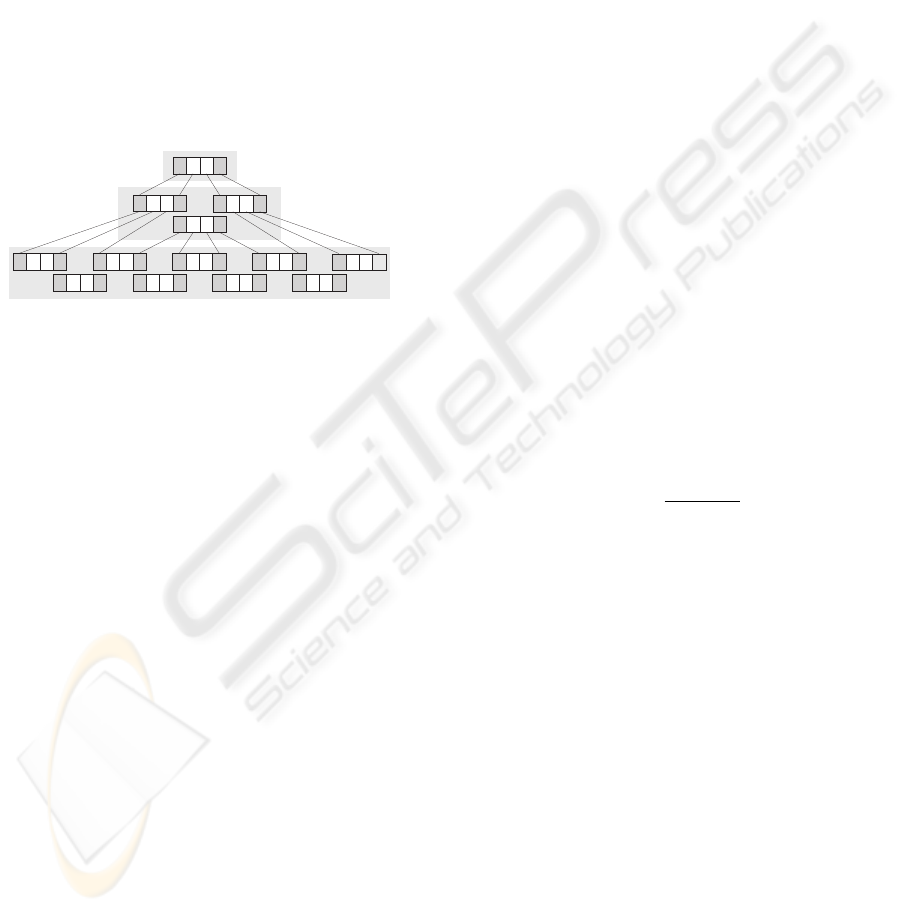
The input states in each particle are printed with dark

background (e.g. S and G in the ﬁrst level) whereas

the optimized states are represented by letters in white

rectangles (e.g. A and B in this level). The ﬁnal path

in the lowest level consists of 27 splines and it is char-

acterized by 28 states of the robot. Such a path can be

found as an extreme of the nonlinear ﬁtness function

in 104-dimensional space (26 optimized states mul-

tiplied by 4 numbers describing each state), which

is difﬁcult (or impossible) in real time applications.

In the hierarchical approach the scanned space is 13

times reduced and the separate optimization subtask

can be done in tens of iterations. Furthermore only

three optimization processes (in the picture marked

by SABG, SCDA, SJKC) are necessary for the be-

ginning of the mission.

S GA B

A B

E F

H I

L M

R T

Y Z

Figure 2: Example of the path decomposition.

2.1 Particle Swarm Optimization

The PSO method was developed for ﬁnding a global

optimum of a nonlinear function (Kennedy and Eber-

hart, 1995),(Macas et al., 2006). This optimization

approach has been inspired by the social behavior of

birds and ﬁsh. Each solution consists of set of pa-

rameters and represents a point in a multidimensional

space. The solution is called ”particle” and the group

of particles (population) is called ”swarm”.

Two kinds of information are available to the parti-

cles. The ﬁrst is their own experience, i.e. their best

state and it’s ﬁtness value so far. The other informa-

tion is social knowledge, i.e. the particles know the

momentary best solution p

of the group found dur-

ing the evaluation process.

Each particle i is represented as a D-dimensional

position vector

−→

(q) and has a corresponding in-

stantaneous velocity vector

−→

(q). Furthermore, it

remembers its individual best value of ﬁtness function

and position

−→

which has resulted in that value.

During each iteration t, the velocity update rule (1)

is applied on each particle in the swarm.

−→

(q) = w

−→

(q − 1) +

+ Φ

(

−→

−

−→

(q − 1)) +

+ Φ

(

−→

−

−→

(q − 1)) (1)

The parameter w is called inertia weight and during

all iterations decreases linearly from w

start

to w

end

The symbols Φ

and Φ

are computed according to

the equation

= ϕ







0 0

0 0 r







(2)

where j = 1, 2. The parameters ϕ

are constants

that weight the inﬂuence of the particles’ own experi-

ence and of the social knowledge. In our experiments,

the parameters were set to ϕ

= 2 and ϕ

= 2. The

, where k = 1 . . . D are random numbers drawn

from a uniform distribution between 0 and 1.

The position of the particles is then computed ac-

cording to the update rule

−→

(q) =

−→

(q − 1) +

−→

(q). (3)

If any component of

−→

is less than −V

max

greater than +V

max

, the corresponding value is re-

placed by −V

max

or +V

max

, respectively, where

max

is the maximum velocity parameter.

Inﬂuencing V

max

in the simple PSO path planning

method (Saska et al., 2006b) illustrated a strong cor-

relation between the optimal value of the parameter

and the space’s size. This size is different for each

optimization process in the hierarchical tree, because

it is constrained by the position of the points S and

G. Therefore the value of V

max

is computed by the

equation

max

||S − G||

, (4)

where c

is a constant that has to be found experi-

mentally.

The update formulas (1) and (3) are applied during

each iteration and the values of p

and p

are updated

simultaneously. The algorithm is stopped if the maxi-

mum number of iterations is reached or any other pre-

deﬁned stopping criteria is satisﬁed.

2.2 Particle Description and

Evaluation

The path planning for a mobile robot can be realized

by a search in the space of functions. We reduce this

space to a sub-space which only contains strings of

cubic splines. The mathematic notation of a cubic

spline (Ye and Qu, 1999) is

g(t) = At

− Bt

+ Ct + D, (5)

where t is within the interval < 0, 1 > and the

constants A, B, C, D are uniquely determined by

the boundary conditions g(0) = P

, g(1) = P

′

(0) = P

′

and g

′

(1) = P

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

118

A = 2P

− 2P

+ P

′

+ P

′

(6)

B = −3P

+ 3P

− 2P

′

− P

′

(7)

C = P

′

(8)

D = P

. (9)

To guarantee continuity in the whole path, every

two neighboring splines in the string must share one

of their terminal states and therefore the actual and the

desired states are deﬁned by initial conditions. The

total number of variables deﬁning the whole path in

2D is therefore only 4(n − 1), where n denotes the

amount of splines in the string. The structure of the

particles used in the optimization process is shown in

Fig. 3.

nspline

1spline

2spline

1,x

1,y

1,x

1,y

2,x

2,y

2,x

2,y

n-1,x

n-1,y

n-1,x

n-1,y

...

Figure 3: Structure of one particle composed of multiple

spline parameters.

The best individual state and the best state achieved

by the whole swarm is identiﬁed by the ﬁtness func-

tion. The global minimum of this function corre-

sponds to a smooth and short path that is safe (i.e.

there is sufﬁcient distance to obstacles).

Two different ﬁtness functions were used in this hi-

erarchical approach. The populations used in the last

hierarchical level (the lowest big rectangle in ﬁgure 2)

are evaluated by the ﬁtness function

= f

length

+ αf

collisions

. (10)

The particles in the other levels are evaluated by the

extended ﬁtness function

= f

length

+ αf

collisions

+ βf

extension

, (11)

where the component f

extension

pushes the con-

trol points of the splines P

to the obstacle free space.

These points are ﬁxed for the lower level planning and

therefore collisions close to these points cannot be re-

paired. The function f

extension

is deﬁned as

extension

(

−2

, if d

< δ

−2

+ p

inside

, else

(12)

where the constant p

inside

strongly penalizes parti-

cles with points P

situated inside of an obstacle (d

is therefore sum of the robot’s radius and radius of the

obstacle) and δ is computed by

δ = min

o∈O

min

∈p

||o − P

||, (13)

where O is the set of all obstacles in the workspace

of the robot. The part f

length

in both ﬁtness functions

corresponds to the length of the path which in 2D case

can be computed by

length

′

(t))

+ (g

′

(t))

dt. (14)

The component f

collisions

penalizes the path close

to an obstacle and it is deﬁned by equation

collisions

(

−2

, if d

< d

−2

+ p

collision

, else

(15)

where p

collision

penalizes paths with a colli-

sion. The penalizations should be in a true relation

inside

>> p

collision

, because collisions far away

from the control points can be corrected in the lower

levels of planning. Parameter that denotes minimal

distance of the path to the closest obstacle is com-

puted by

d = min

o∈O

min

t∈<0;1>

||g(t) − o)||. (16)

Constants α and β in equations 10, 11 determine

the inﬂuence of the obstacles on the ﬁnal path.

3 RESULTS

The presented algorithm was intensively tested in two

experiments. During the ﬁrst one the parameters of

the Particle Swarm Optimization were adjusted un-

til an optimal setting was found. In the second ex-

periment the approach was compared with the sim-

ple PSO path planning method that was published in

(Hess et al., 2006).

The scenario that was used in both experiments

was motivated by landscapes after a disaster. In

such workspace there are several big objects (facto-

ries, buildings, etc.) with a high density of obstacles

(wreckage) nearby. The rest of the space is usually al-

most free. In our testing situation we randomly gen-

erated 20 of such clusters with an uniform distribu-

tion. Around each center of the cluster 100 obstacles

were positioned randomly followed by the uniform

distribution of another 1000 obstacles in the complete

workspace.

For the statistic experiments a set of 1000 ran-

domly generated situations was generated. We chose

a quadratic workspace with a side length of 1000 me-

ters and circular obstacles with a radius of 4 meters.

HIERARCHICAL SPLINE PATH PLANNING METHOD FOR COMPLEX ENVIRONMENTS

119

Table 1: Amount of paths that intersect with an obstacle.

The size of the test set is 1000 situations where the hierar-

chical algorithm was interrupted in the third level.

max

0.01 0.1 1 10 30 100

0.2 171 170 177 177 214 537

0.5

179 190 180 169 218 479

401 350 239 170 210 450

876 882 652 195 206 404

928 917 877 229 202 350

The prepared scenario was modiﬁed in order to get

signiﬁcant and transparent results: The radius of the

obstacles was dilated by the robot radius and there-

fore the path outside the obstacles is considered as

collision free. All obstacles around the robot’s start-

ing and goal position, that were closer than 10 times

the robot’ radius were removed from the scenario. Be-

cause the situations where these points lie in a cluster

are unsolvable.

In the ﬁrst experiment the inﬂuence of the parame-

ters w

start

and V

max

on the optimization process was

studied. All results were obtained with the following

PSO constants: w

end

= 0.2, ϕ

= 2, ϕ

= 2. The

population was set to 30 particles and the computa-

tion was stopped after 30 iterations. The resulting tra-

jectories were composed of 27 splines, because each

vector p used in the optimization process corresponds

to three splines and the hierarchical algorithm was in-

terrupted in the third level as it is illustrated in Fig. 2.

The interruption of the algorithm at a ﬁxed time (even

if no collision free path was found) is necessary for a

reasonable comparison of the different parameter set-

tings.

The amount of ﬁnal paths with one or more colli-

sions obtained by the experiments with different set-

tings of w

start

and c

(equations (1) and (3)) are pre-

sented in table 1. More than 84 percents of the sit-

uations were solved ﬂawlessly by the algorithm with

the optimal values of the constants (w

start

= 0.5 and

= 3) already in the third level of the hierarchi-

cal process. Looking at the table it can be seen that

the fault increases with a deﬂection of both parame-

ters from this optima. Too big values of c

(result-

ing in small values of the maximum particle veloc-

ity) block the particles to search a sufﬁcient part of

the workspace and contrariwise small values of c

change the PSO process to a random searching. Like-

wise too big values of the maximum inertia w

start

fa-

cilitate the particles to leave the swarm and the search-

ing process is again a random walk. Finally too small

values of w

start

push the particles to the best local

solution and the population diversity is lost too early.

Table 2 depicts the mean ﬁtness values and the

corresponding covariances of the collision free paths

Table 2: Mean value and covariance of the best ﬁtness val-

ues after 30 iterations.

max

0.1 1 10 30

0.2 1.40(1.2) 1.36(0.7) 1.26(0.2) 1.32(1.3)

0.5

1.42(1.5) 1.39(1.6) 1.25(0.1) 1.30(0.6)

1.82(6.2) 1.59(2.5) 1.27(0.2) 1.29(0.4)

2.81(23) 2.47(16) 1.30(0.3) 1.28(0.6)

Table 3: Number of paths which intersect with an obstacle

found by the hierarchical and the simple PSO algorithm.

maximum level

I II III IV V

iterations 30 117 272 568 1103

hierarchical 923 490 159 87 65

simple(n = 2)

809 592 481 457 411

simple(n = 3)

923 634 505 443 405

simple(n = 4)

992 821 645 599 526

obtained in the experiment described above. These

numbers provide a comparison of the mean quality of

the paths for different combinations of PSO settings

within the meaning of the required features. The op-

timal value of w

start

is the same as in table 1, but the

optimal constant c

is bigger than before. The stricter

restriction of the maximum velocity forces the parti-

cles to search closer to the best member, that may not

be collision free at the moment. The ﬁnal path then

can be smoother and shorter, but the ability to over-

come this local minima and to ﬁnd a collision free

path is lower.

An example of a randomly generated situation with

a solution found by the algorithm using the optimal

parameters is shown in Fig. 4. Looking at Fig. 5 and

6, the decreasing amount of collisions in the path at

different hierarchical levels can be observed. The so-

lution found in the ﬁrst step (dotted line) contains 21

collisions along the whole path, but the control points

are situated far away from the obstacles and therefore

the big clusters are avoided. Only 4 collisions are con-

tained in the corrected path at the second level (dashed

line) and the ﬁnal solution (solid line) after three hi-

erarchical optimizations is collision free.

In the second experiment the usage of the hierar-

chical method better agrees with a real application.

The stoping criterion now also considers the number

of collisions in the appropriate spline in addition to

the preset maximum hierarchical level. Collision free

parts of the solution do not need to be corrected in

the lower levels and thus the total number of itera-

tions is reduced. The maximum level as a part of the

stopping criterion is still important, because a colli-

sion free path may not exist and also a different ﬁtness

function (equation 10) is applied in the lowest level.

Table 3 shows a comparison between the hierarchi-

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

120

Figure 4: Situation with 3000 randomly generated obstacles. Dotted line - path found in the ﬁrst level, dashed line - path

found in the second level, solid line - ﬁnal solution found in the third level.

cal and the simple methods. The second row of the

table consists of the mean amount of iterations exe-

cuted by the PSO modules in the hierarchical algo-

rithm with different settings of the maximum level.

These values acted as inputs for the relevant runs of

the simple PSO algorithm that was run with different

numbers of splines (other parameters were set accord-

ing to (Saska et al., 2006b)).

The number of solutions that intersect with an ob-

stacle are displayed in the last four rows of the table.

Already in the third level, the presented hierarchical

approach achieved a result which is several times bet-

ter then the other algorithms. The computation reduc-

tion could be obtained, because the number of splines

was increased depending on the environment’s com-

plexity, but the size of the searched space remained

unchanged. The simple PSO method applied with a

number of populations lower than 300 obtained the

best results by using the shortest particle (only two

splines in the string). If the evolution process was

stopped after 1000 iterations, the optimal path was

composed of three splines. We suppose that the op-

timal length increases with the duration of the evolu-

tion, because a more complicated path allows to ﬁnd

a collision free solution in the complex environment.

But due to the extension of the calculation time it is

not applicable in real time applications.

4 CONCLUSIONS AND FUTURE

WORK

In this paper a novel hierarchical path planning

method for complex environments was presented.

The developed algorithm is based on the optimization

of cubic splines connected to smooth paths. The ﬁ-

nal solution is optimized by repeatedly used PSO for

collision parts of the path. The approach was inten-

sively veriﬁed in two experiments with 1000 random

generated situations. Each scenario, that was inspired

by a real environment, contained more than 2000 ob-

stacles.

The results of the experiments proved the ability

of the algorithm to solve the path planning task in

very complicated maps. Most of the testing situa-

tions were solved during the ﬁrst ﬁve hierarchical lev-

els and therefore the ﬁrst ﬁnal path of the robot was

HIERARCHICAL SPLINE PATH PLANNING METHOD FOR COMPLEX ENVIRONMENTS

121

mum 121 runs are necessary for the whole path). It

makes the algorithm usable in real time applications,

because the mission can be started already after 4 per-

cent of the total computational time and the rest of the

solution will be found during the robot’s movement.

Figure 5: Zoomed part of ﬁgure 4 close to the goal position.

Figure 6: Zoomed part of ﬁgure 4.

The optimal adjusted approach failed in the 6.5 per-

cent of the runs. In approximately 80 percent of these

unresolved situations a collision free solution did not

exist (due to unsuitable position of the random gen-

erated clusters) or could not be found during only

ﬁve hierarchical levels (part of the workspace was too

complicated). But error in 20 percent of the unre-

solved situations (about one percent of the total runs)

was caused by a placing of the control points near an

obstacle, in spite of the penalization p

inside

in the ﬁt-

ness function 11. This problem can be solved using

constrained optimization methods (Parsopoulos and

Vrahatis, 2006),(Vaz and Fernandes, 2006), that guar-

antee fulﬁllment of the constrictions.

In future we would like to extend the algorithm to

be utilizable in dynamical environments. Only the rel-

evant part of the solution could be corrected due to

the decomposition of the total path. Other computa-

tional reduction could be achieved by using the old

cultivated population for the optimization of a partly

changed ﬁtness function.

Also the stoping rules for the PSO module or for

the hierarchical sinking need to be improved. The cri-

teria should be combined with physical features of the

solution, because the ﬁxed number of iterations and

levels must be determined for the speciﬁc situation.

Therewithal a superior solution can be obtained faster

by a more sophisticated setting of the PSO parame-

ters. Experiments showed that using the same values

of the constants in all levels is not the best solution

which gives scope for an innovation (Beielstein et al.,

2002).

Another stream will be focused on testing and

comparing different optimization methods (e.g. ge-

netic algorithms (Tu et al., 2003), simulated annealing

(Janabi-Shariﬁ and Vinke, 1993), (Martinez-Alfaro

and Gomez-Garcia, 1998) or ant colony (Liu et al.,

2006)). We also plan to adapt the PSO algorithm for

this special task. The main idea is to use the pleasant

feature of the Ferguson splines. The control points

lie on the path (opposite for example in the robotic

often used Coons curves (Faigl et al., 2006)) and so

it is possible to put the initial population for instance

on the shortest path in the Voronoi diagram (Auren-

hammer and Klein, 2000) or in the Transformed net

(Saska et al., 2006a). This innovation reduces the

computational time, because the exploratory mode of

the particle swarm optimization can be skipped.

ACKNOWLEDGEMENTS

This work was supported by the Elitenetwork of

Bavaria through the program ”Identiﬁcation, Opti-

mization and Control with Applications in Modern

Technologies”.

REFERENCES

Aurenhammer, F. and Klein, R. (2000). Voronoi diagrams.

Hand book of Computational Geometry. Elsevier Sci-

ence Publishers, Amsterodam.

Azariadis, P. and Aspragathos, N. (2005). Obstacle

representation by bump-surface for optimal motion-

planning. Journal of Robotics and Autonomous Sys-

tems, 51/2-3:129–150.

Beielstein, T., Parsopoulos, K. E., and Vrahatis, M. N.

(2002). Tuning pso parameters through sensitivity

analysis. In Technical Report, Reihe Computational

Intelligence CI 124/02., Collaborative Research Cen-

ter (Sonderforschungsbereich) Department of Com-

puter Science, University of Dortmund.

Borenstein, J. and Koren, Y. (1991). The vector ﬁeld his-

togram: Fast obstacle avoidance for mobile robots.

IEEE Journal of Robotics and Automation, 7(3):278–

288.

ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics

122

Eberhart, R. C. and Kennedy, J. (1995). A new optimizer

using particle swarm theory. In Proceedings of the

Sixth International Symposium on Micromachine and

Human Science., pages 39–43, Nagoya, Japan.

Faigl, J., Klacnar, G., Matko, D., and Kulich, M. (2006).

Path planning for multi-robot inspection task consid-

ering acceleration limits. In Proceedings of the four-

teenth International Electrotechnical and Computer

Science Conference ERK 2005, pages 138–141.

Franklin, W. R., Akman, V., and Verrilli, C. (1985). Voronoi

diagrams with barriers and on polyhedra for minimal

path planning. In Journal The Visual Computer, vol-

ume 1(4), pages 133–150. Springer Berlin.

Hess, M., Saska, M., and Schilling, K. (2006). Formation

driving using particle swarm optimization and reactive

obstacle avoidance. In Proceedings First IFAC Work-

shop on Multivehicle Systems (MVS’06), Salvador,

Brazil.

Janabi-Shariﬁ, F. and Vinke, D. (1993). Integration of the

artiﬁcial potential ﬁeld approach with simulated an-

nealing for robot path planning. In Proceedings of 8th

IEEE International Symposium on Intelligent Control,

pages 536–41, Chicago, IL, USA.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. In Proceedings International Conference on

Neural Networks IEEE, volume 4, pages 1942–1948.

Khatib, O. (1986). Real-time obstacle avoidance for manip-

ulators and mobile robots. In The International Jour-

nal of Robotics Research, volume 5, pages 90–98.

Kunigahalli, R. and Russell, J. (1994). Visibility graph ap-

proach to detailed path planning in cnc concrete place-

ment. In Automation and Robotics in Construction XI.

Elsevier.

Latombe, J.-C. (1996). Robot motion planning. KluverAca-

demic Publishers, fourth edition.

Liu, S., Mao, L., and Yu, J. (2006). Path planning based on

ant colony algorithm and distributed local navigation

for multi-robot systems. In Proceedings of IEEE In-

ternational Conference on Mechatronics and Automa-

tion, pages 1733–8, Luoyang, Henan, China.

Macas, M., Novak, D., and Lhotska, L. (2006). Particle

swarm optimization for hidden markov models with

application to intracranial pressure analysis. In Biosig-

nal 2006.

Martinez-Alfaro, H. and Gomez-Garcia, S. (1998). Mobile

robot path planning and tracking using simulated an-

nealing and fuzzy logic control. In Expert Systems

with Applications, volume 15, pages 421–9, Monter-

rey, Mexico. Elsevier Science Publishers.

Nearchou, A. (1998). Solving the inverse kinematics prob-

lem of redundant robots operating in complex envi-

ronments via a modiﬁed genetic algorithm. Journal of

Mechanism and Machine Theory, 33/3:273–292.

Parsopoulos, K. E. and Vrahatis, M. N. (2006). Parti-

cle swarm optimization method for constrained op-

timization problems. In Proceedings of the Euro-

International Symposium on Computational Intelli-

gence.

Saska, M., Kulich, M., Klan

car, G., and Faigl, J. (2006a).

Transformed net - collision avoidance algorithm for

robotic soccer. In Proceedings 5th MATHMOD

Vienna- 5th Vienna Symposium on Mathematical

Modelling. Vienna: ARGESIM.

Saska, M., Macas, M., Preucil, L., and Lhotska, L. (2006b).

Robot path planning using partical swarm optimiza-

tion of ferguson splines. In Proc. of the 11th IEEE

International Conference on Emerging Technologies

and Factory Automation. ETFA 2006.

Tu, J., Yang, S., Elbs, M., and Hampel, S. (2003). Genetic

algorithm based path planning for a mobile robot.

In Proc. of the 2003 IEEE Intern. Conference on

Robotics and Automation, pages 1221–1226.

Vaz, A. I. F. and Fernandes, E. M. G. P. (2006). Optimiza-

tion of nonlinear constrained particle swarm. In Re-

search Journal of Vilnius Gediminas Technical Uni-

versity, volume 12(1), pages 30–36. Vilnius: Tech-

nika.

Ye, J. and Qu, R. (1999). Fairing of parametric cubic

splines. In Mathematical and Computer Modelling,

volume 30, pages 121–31. Elseviers.

HIERARCHICAL SPLINE PATH PLANNING METHOD FOR COMPLEX ENVIRONMENTS

123